基于关系网络的教育中同伴效应估计
——来自一所初中的证据
冯 晗
(杭州师范大学 经济学院, 杭州 310012)
一、引言
学生在成绩、偏好、行为等方面的相互影响,亦即同伴效应,同伴效应是近年来教育和经济相关研究的热点话题之一。来自不同国家、基于不同方法、针对不同方面的研究,也普遍确认了同伴效应的存在[1-3]。在中国,近年来的不少研究也找到了同伴效应存在的证据[4-11]。
理论设想中的同伴可能是自发地在学习、生活上有频繁接触的一些个体,比如,朋友。但在实践中,当前大部分研究对同伴的定义,通常都会依赖于某种外生的群组。比如将处于同一学校[12]、年级[4, 13-15]、宿舍[5,16,17]、班级[7,8,9,11,18,19]或者是社区[10,20]的学生定义为同伴,计算出每个群组中其他学生的平均成绩或其他特征作为核心解释变量,再估计它对学生成绩或其他方面的影响。这种做法的好处是外生的群组定义有助于减少内生性的可能,但其代价,则是会忽略掉群组内部的异质性,尤其是因成员间关系密切程度不同所导致的异质性。同学未必是朋友,而朋友之间和普通同学之间的相互影响可能存在显著差异。用群组其他学生的平均特征来估计同伴效应,则忽略了差异。
现有研究的结果,也在强调区分同学间不同关系的重要性。比如袁舟航等(2018)估计了一起学习的同伴间的同伴效应,结果发现其数值远大于此前研究所估计出的班级其他同学带来的同伴效应[6]。除了大小,朋友和普通同学之间的相互影响,在机理上也有可能不一致。比如Hoxby(2000)的结果表明,同年级中女同学比率上升,对男生的成绩存在正面影响[13];Lu和Anderson(2013)发现教室内座位周边女生增加,并不会给男生的成绩造成显著影响[21];而Hill(2015)却发现,朋友中女性比率上升,会给男生带来显著的负面影响[20]。
此外,单纯估计群组内其他同伴的平均影响,还可能给政策制定者一个错误的暗示:基于历史估计结果,简单地调整学生在不同群组间的分配,就能通过同伴效应,来对学生施加最佳的影响。但实际上,这样的分配变化,却很有可能会导致学生间朋友关系网络的复杂变化,从而给最终的同伴效应造成预料以外的影响。Carrell等(2013)在美国一所大学所做的尝试就失败了。在按照他们精心设计的最优方案重新分班之后,学生,尤其是差生的成绩非但没有上升,反倒出现了显著的下降[22]。此后,Booij等(2017)在阿姆斯特丹大学新生中所做的实验也发现,班级内学生之间成绩差异越大,差生与其他学生间互动就越少[23]。这意味着如果将某个差生放到成绩更好的班内,虽然其同班同学的平均成绩会提高,但他每天互动的真实同伴的平均成绩,却未必会提高。分班调整对差生成绩的影响,因而也就难以预测。总之,无论是从理论还是从政策含义出发,都有必要在估计同伴效应时区分同一群组内部学生间的不同关系,尤其是要区分关系密切的朋友和普通同学,这既有助于更深刻地理解同伴效应的机理,也有助于利用它,来设计更有针对性的政策工具。
不过,要做到这一点并不容易。困难一方面来源于数据的可得性上,与成绩等信息不同,学生间的朋友关系难以观测,目前绝大部分用于同伴效应估计的数据集都不包含朋友关系信息。尤其是在国内,据笔者所知,目前还没有任何公开微观调查数据包含学生间朋友关系信息。只有少数基于独有调查数据的研究,会使用类似信息。比如袁舟航等(2018)在安徽部分农村小学进行问卷调查时,要求学生报告一位本班级内与其一起学习的最重要同伴。基于这个数据,他们估计了这个同伴对学生成绩的影响。而他们的估计也发现,这个同伴会对学生的成绩产生的影响,远大于以往利用群组内同伴平均特征所估计的同伴效应[6]。
估计朋友间同伴效应的另一大困难在于朋友选择的强烈内生性。物以类聚,人以群分。不少研究都发现,在成绩等各种特征上更相似的学生,更容易成为朋友[3]。要识别出朋友间同伴效应存在的可靠证据,就必须要设法消除这种内生性。在数据选择本就不多的情况下,这自然更进一步提高了研究的难度。
不过,近年来在关系网络和同伴效应研究上的进步,使得克服以上困难成为可能。如果将朋友视作学生间的一种联系,在对某组学生间的朋友关系做全面观察的基础上,就能刻画出这些学生之间的一个完整关系网络。Bramoulle等(2009,2020)指出,基于这一关系网络,就有多种方法来构建工具变量,消除朋友关系形成中的内生性,实现对同伴效应的估计[3,24]。而其中最方便,要求也最简单的方法,就是利用网络中朋友的朋友(即“二阶朋友”(1)假设有A、B、C、D四个学生。其中A、B、C互为朋友,而D则是B的朋友。此时,B没有二阶朋友,而A和C的二阶朋友都是D,D的二阶朋友则是A和C。)的各种特征作为朋友相应特征的工具变量。
这一思路进一步提高了研究对数据的要求:不仅需要知道每个学生的朋友是谁,还需要知道完整的关系网络。不过,当下已有不少研究开始基于这一思路来识别多个方面的同伴效应。比如Nicoletti等(2018)用姐妹的女邻居在生育子女后的劳动供给情况,作为姐妹生育后劳动供给的工具变量,估计了姐妹间在生育后劳动供给上的同伴效应[25]。而De Giorgi等(2020)用同事的配偶的同事的消费,作为同事消费的工具变量,估计了同事间在消费上的同伴效应[26]。
本文的研究也将基于这一思路展开。本文作者在浙江省某地级市市辖区的一所初中与校方合作,进行了一次全面的问卷调查,实现了对此学校某届学生间关系网络的完整观察,基于此计算了所有学生二阶朋友的平均成绩,并将此作为朋友成绩的工具变量,进而讨论朋友间在成绩上的相互影响。
研究结果表明,在排除掉人以群分的影响之后,同学间仍然存在着显著的近朱者赤现象:即使是在相对同质的同伴环境下,朋友间在学习成绩上仍然表现出了显著的相互影响。并且这一影响要大于普通同学间的同伴效应。这进一步佐证了本文开头的论断:相比一般同学间的相互影响,朋友间的同伴效应,可能是更具理论和现实价值的研究对象。
本文的研究可能是国内第一次基于对关系网络的完整观测来识别同伴效应的尝试,与袁舟航等(2018)中所使用的“一起学习的伙伴”[6]不同的是,本文中学生报告的是“朋友”,后一概念更一般化,这既方便了对关系网络的完整观测,也有助于提高本文研究结果与未来更深入研究的可比性。
二、数据与模型介绍
(一)数据来源与背景
本文所使用的数据来源于浙江某地级市市辖区的一所公立初中。当地2019年人均GDP为82340元,高于全国平均,但低于浙江省当年平均水平。当地义务教育实行划片招生,作为一所非重点初中,样本初中缺乏挑选生源的能力,因而在生源上具有一定代表性。笔者从这所学校获取了2018届12个班所有毕业学生的历次考试成绩和相关个人信息,还在2017年,也就是这些学生初三第一学期刚开学时,通过学校进行了一次全面的问卷调查,在问卷中除了要求学生报告一些家庭相关信息外,还要求他们列出自身最要好的五个朋友(2)问卷中的具体问题为:“请写出最多五个你最要好朋友的名字”,随后在题后给出了五个空位用于书写名字。此外,问卷中还包含另一个相关问题:“你最经常跟朋友一起做的事情是:”,包含五个选项:“学习”“运动”“阅读”“游戏”和“其他”。,并基于此构建了完整的学生间关系网络。
与以往研究随机抽取学校,再在学校中随机抽取班级不同,本文是对特定学校某届学生的完整观测,这有助于观察到完整而非局部的关系网络,从而基于关系网络信息实现对同伴效应的识别。此外,这所初中在学生入学时,会按照入学成绩,分性别从高到低蛇形排列的方式,将学生分配到各个班级。具体而言,入学成绩排名第一到第十二的男生,分别被分配到1到12班,而十三到二十四名的男生,则按照倒序分配给12到1班,女生与此类似。如图1所示,这一做法保证了各个班的规模和初始入学平均成绩差异不大,Kruskal-Wallis检验也证实了这一点(3)Kruskal-Wallis检验旨在检验不同组样本之间是否存在显著差异。其初始假设为各组样本均从同一个总体中随机抽样得到。本文用语数外三门课成绩在12个班之间所做的Kruskal-Wallis检验,所获得的P值均大于0.15,意即从成绩看,无法拒绝各班从同一总体中随机抽样获得的初始假设,或者说,各班之间不存在显著的初始差异。,这有助于消除分组内生性。
样本学生在入学时共有532人,在三年中,31人转走,16人转入(4)这些转走的学生入学成绩与留下的学生没有显著区别。而转入的学生毕业成绩显著低于其他学生,不过鉴于转入学生占学生总数的比率不到4%,本文未在分析中考虑他们的影响。,最终毕业参加中考的人数为517人,其中501人既有入学成绩、也有中考成绩信息,这501人均填写了问卷,从而构成了本文分析的核心样本。
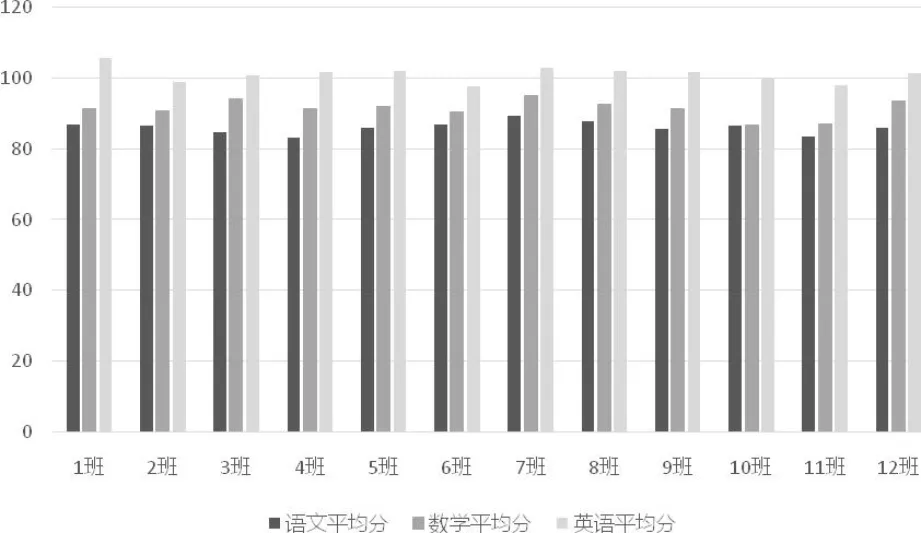
图1 各班入学平均分
为确保朋友关系识别准确,在本文中,只有当两个学生互相都将对方列为朋友时,才被认为是一对朋友。
在501名填写了问卷的学生中,有360名学生至少有一个朋友。样本中共有448对朋友,其中408对是同班同性同学之间。
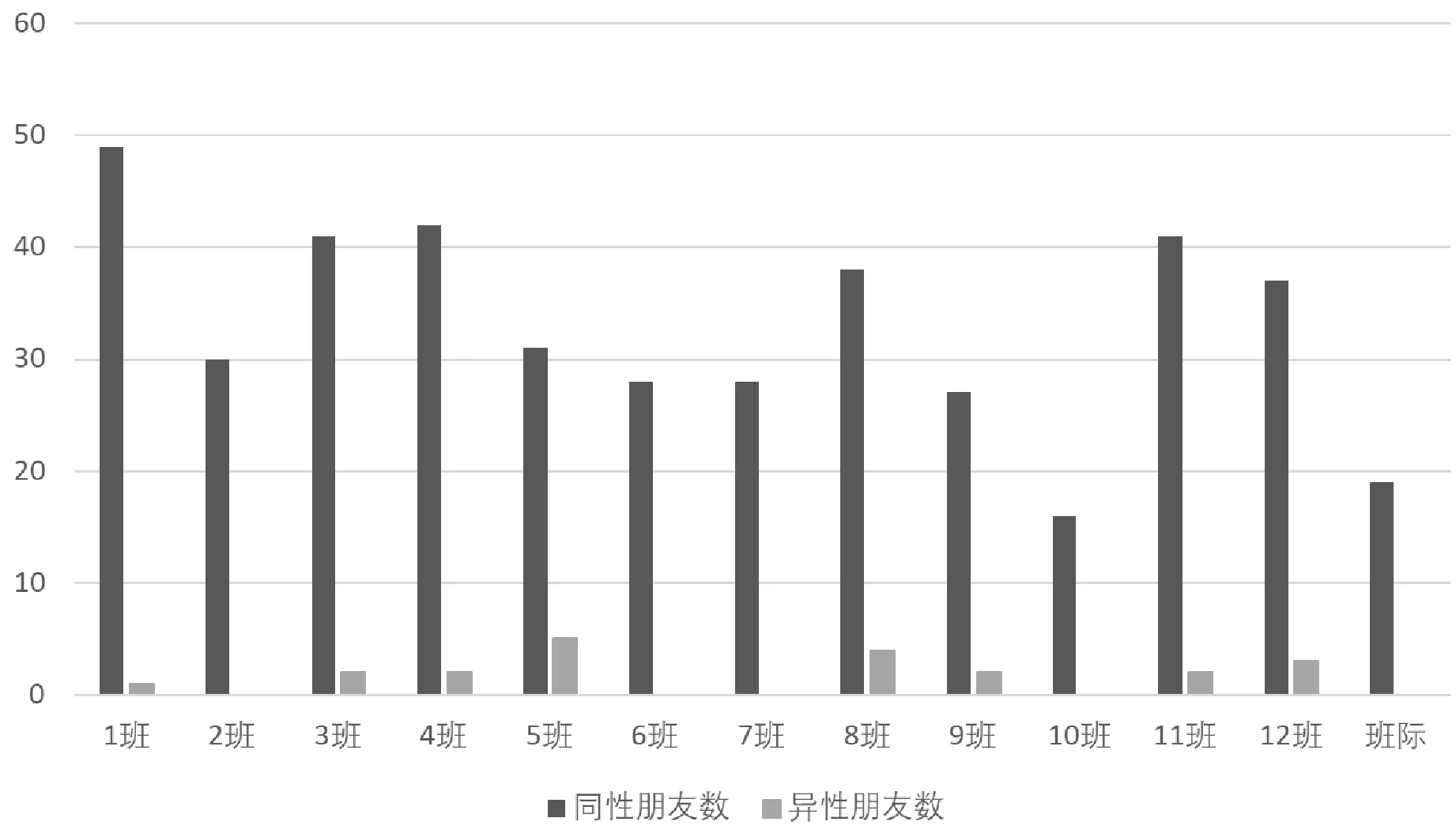
图2 各班朋友数分布情况
图2中画出了各个班级和班际的同性和异性朋友数。与初始成绩不同的是,各班之间在朋友分布上存在较大差异。本文样本中的朋友关系网络稀疏程度非常适合用于识别同伴效应:一方面,大多数学生至少有一个朋友,另一方面,朋友网络又不过密,在排除掉直接的朋友之后,仍有311位学生至少有一个二阶朋友。
(二)模型构建
本文所用的基本模型可由下式表示:
(1)
下标i和c分别表示不同学生个人和班级。Hi,c为毕业考试,亦即中考成绩,Mi,c为入学考试,亦即小升初考试成绩。当地有一所重点初中(非样本学校),每年小升初考试成绩最高的学生,有机会进入那所重点初中,中考成绩同样会影响学生能否进入重点高中,因而这两次考试无论是学生、家长还是学校和老师,重视程度均远高于其他考试,适合用于构建核心变量。同时,为了消除不同次和科目考试难度/总分上的差异,提高结果的可比性,本文回归中所有的考试成绩均作了减去均值再除以标准差的标准化处理。在标准化处理时,参加相应考试的所有学生,无论他/她是否出现在最终回归的样本中,都被纳入考虑。此外,为了消除Reflection Problem[27],避免朋友或同学间在成绩上的相互影响导致回归系数被高估,本文使用标准化后的中考成绩作为被解释变量,而基于小升初考试的成绩来构建各个解释变量。后一考试在所有学生入学之前进行,因而存在学生间相互影响的可能性较低,受其他同学、朋友中考成绩影响的可能性更低。具体在回归当中,本文研究主要关心语数外三门主课的成绩,分别基于这三门课的成绩,构建各个相关变量。

首先,如果将这些没有朋友的学生的朋友平均成绩定义为缺失值,那就会导致这些观测值被排除出回归。这不但会导致样本容量缩小,更关键的问题在于,这样的缩小还是非随机的:显然,有朋友的学生和没有朋友的学生,很可能存在系统性差异。因此排除这些样本,可能导致非随机取样,使估计结果有偏。
其次,将没有朋友的学生的朋友平均成绩定义为0,实际上假设了没有朋友,与朋友平均成绩为0是等同的。这的确不是一个合理的假设。但在同时控制是否有朋友这一变量的情况下,没有朋友的学生,与朋友平均成绩为0学生之间的差异,是可以被这个变量所捕捉的。因而在控制这个变量的情况下,本文模型并不需要没有朋友与朋友平均成绩为0等同这一假设。
事实上,在控制是否有朋友变量的情况下,将没有朋友的学生的平均成绩定义为0或者任何其他常数,都只会改变是否有朋友这一变量的系数,而不会改变任何其他参数的估计值。换言之,这一设定对本文核心结论没有影响。
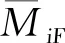
这一工具变量有效的前提是二阶朋友不会直接影响学生的成绩,为此本文已经从二阶朋友中排除了每个学生自身和他的直接朋友,不过即使如此,二阶朋友仍然可能从两个方面对学生成绩产生影响。
一方面,是部分朋友关系可能会被忽略。与学界常用的美国国家青少年到成人健康长期调查(Add Health,The National Longitudinal Study of Adolescent to Adult Health)问卷相似,本文问卷中要求学生最多报告五个朋友,这样一个拥有超过五个朋友的学生,其部分朋友关系就可能被忽略。不过,在本文样本中,360个至少有一个朋友的学生里,只有17个列出了5个朋友,占比不到5%。其他人既然并没有用完五个朋友的配额,当然不太可能存在未观测到的朋友。
另一方面,即使不是朋友,一个班级内的学生仍然可能会存在其他方面的相互影响。为此,本文在回归里控制了班级其他学生的平均入学成绩和班级固定效应vc,这应当有助于缓解这方面的担心。
与此前类似地,对没有二阶朋友的学生,其二阶朋友平均成绩值被设定为0,工具变量回归中还加入了是否有二阶朋友虚拟变量,其理由与将没有朋友学生的朋友平均成绩设定为0类似,不再赘述。具体地,本文工具变量回归的一阶段回归方程可由下式表示:
(2)
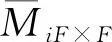
(三)各变量描述性统计
本文样本中学生和老师各项基本信息的描述性统计如表1所示。虽然回归中任课老师信息均被班级固定效应吸收,不过表1中仍报告了老师的年龄、工龄、性别、职称等特征的统计信息。
样本中的父母均至少初中毕业,因而在表1中,只报告了父母各自是否高中和大学毕业信息。表中数据显示,即使在标准化后,不同科目的成绩仍然存在较大差异。考虑到不同科目所要求的能力有所差异,且已有不少研究显示不同科目成绩上的同伴效应存在显著差异。因而在回归中也将这些科目分别处理。此外,在入学和毕业成绩、朋友数等多个方面,男生和女生之间都存在显著差异,这也将是本文此后异质性同伴效应分析的一个重点。
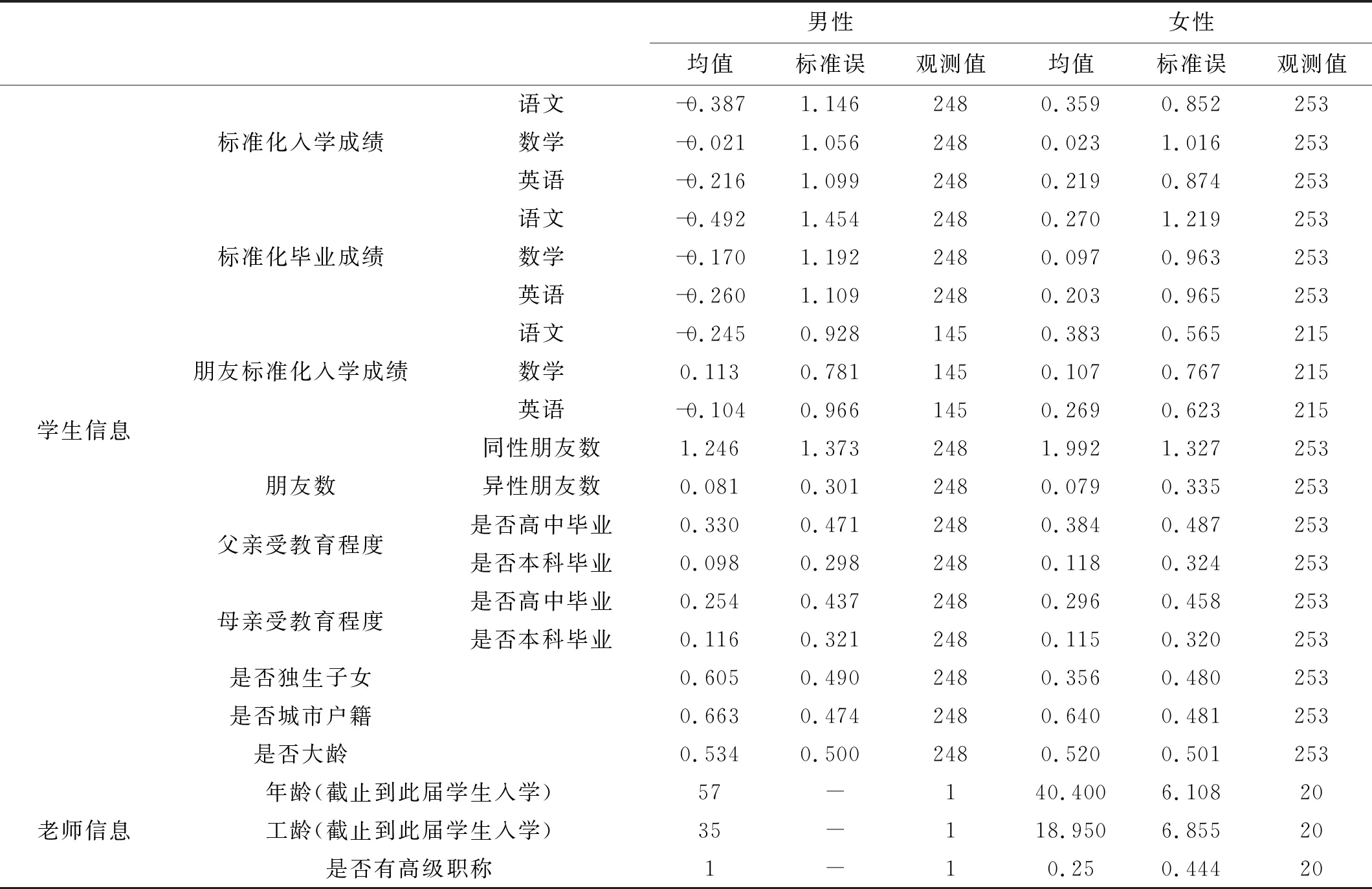
表1变量描述性统计
三、实证结果
(一) 基本结果
表2是研究的基本回归结果。为了消除潜在的异方差问题,此处报告的是在班级*性别层面上聚类的稳健标准误(7)回归中仅有12个班级,因而无法仅在班级层面上聚类。。
相比以往研究,表2回归中班级同学平均成绩变量在各个回归中至多只有微弱的显著性,这可能是因为样本所有班级均来自同一个学校,学生间差异较小,再加上入学时的蛇形分班安排和相对较大的班级规模(每个班均有40多人)(8)这个规模在国内不算大,不过相比很多针对发达国家样本所做的研究偏大。比如Burke和Sass(2013)[32]的样本中,平均每个班级仅有不到30人。,这样在控制班级固定效应的情况下,班级同学平均成绩变量的离差不大,在回归中也就很难表现出显著性。
而研究最关心的朋友平均成绩变量,则有着与班级同学平均成绩完全不同的表现,这也佐证了此前的论断:朋友之间的相互影响,和班级普通同学之间的相互影响,有着不同的作用机理。在表2当中,虽然用语文成绩所做的回归并不显著,但无论是OLS还是工具变量回归的结果,都表明有英语或数学成绩更好的朋友,会给学生相应课程的成绩带来正面的影响。
表2的结果还表明,朋友影响不仅是显著的,还在不同科目之间存在显著差异。朋友对数学成绩的影响要大于英语成绩,而后者又要大于语文成绩。类似的现象在此前研究中也有发现,比如,Zhao(2015)基于中国19个城市数据的研究发现,参加课外辅导班会显著提高学生的数学成绩,但对语文成绩却影响甚微[28]。具体到同伴效应上,Carman & Zhang(2012)和Wang等(2018)基于中国数据的研究,也都发现,数学成绩上的同伴效应要显著强于语文和英语成绩上的[29,30]。
这种差异可能是源于不同科目对认知能力要求上的差异。Neidell&Waldfogel(2010)发现在对认知能力要求较强的课程中,同伴效应会更加明显[31]。而在语数英这三门课当中,显然对于中国学生而言,数学对认知能力的要求最高,而作为母语的语文则要求最低。

表2基本回归结果
此外,如前所述,本研究的工具变量为二阶朋友平均成绩和是否有二阶朋友,并且所有没有二阶朋友的学生,其二阶朋友平均成绩均被设定为0。这样所有没有二阶朋友的学生,其工具变量值都没有变化,即使这些学生本身有朋友,且朋友的平均成绩不为零,一阶段回归估计的平均成绩拟合值也不会有变化。因而这部分样本无法对工具变量回归结果产生任何影响,这使得工具变量估计的系数,主要来源于有二阶朋友,因而朋友平均成绩拟合值存在变化的那部分样本。
与此相对应的是,OLS回归中,即使没有二阶朋友,只有直接朋友的个体,其一阶朋友平均成绩也存在变化,因而也会影响到回归的系数。而如此前所述,360名至少有一个朋友的学生里,只有311名至少有一个二阶朋友。这导致工具变量回归和OLS回归所针对的局部有所差异。表2中同一门课两组回归结果之间在拟合优度上的差异,也可以帮助说明这一点。
而本文数据中,有二阶朋友的个体,无论在自身成绩还是朋友的平均成绩的均值上,均显著高于有直接朋友的样本,更显著高于全样本平均(9)以英语成绩为例,标准化后全样本英语平均成绩接近0,而有朋友和有二阶朋友样本的英语平均成绩则分别为0.113和0.145。。与此同时,如同此后异质性检验中所给出的那样,无论是自身成绩的提高还是朋友平均成绩的提高,都意味着来自朋友同伴效用的增强。这可能可以解释为何表2中工具变量回归系数要大于OLS回归系数。
在数值上,本文朋友成绩的系数,大于此前研究估计的班级同学之间的相互影响,而与袁舟航等(2018)估计的一起学习的同伴间的相互影响不相上下(10)袁舟航等(2018)的估计主要关注数学成绩,而本文基于数学成绩所估计的结果中,OLS的系数比他们的小,而IV的系数则比他们的大[6]。。
在每门课的OLS和工具变量回归的基础上,为了检验OLS的内生性,表2中还报告了Durbin-Wu-Hausman Test的结果。在基于数学和英语成绩的回归中,这一检验的结果均保持显著为正,这说明OLS的结果的确存在内生性,因而在此后的回归中,若无特殊说明,本文都将报告工具变量估计的结果。
(二) 工具变量有效性检验
为了评估了本文所用工具变量的有效性,表3首先给出了表2报告的每个工具变量回归的一阶段回归和过度识别检验结果。在每个回归当中,工具变量二阶朋友平均成绩均在1%程度上显著,Cragg-Donald Wald F统计量同样显著,说明工具变量对内生变量有较强的解释能力,不存在弱工具变量问题。相反,过度识别检验的结果则不显著。

表3工具变量有效性检验
除此之外,本文还在三门课的回归中均同时加入四个工具变量,即二阶朋友平均的入学语文、数学和英语成绩,以及是否有二阶朋友虚拟变量,从而更好地利用过度识别检验来检验工具变量的有效性。这些结果报告在表3多IV结果列当中。它们表明,同时引入多个工具变量导致的多重共线性轻微降低了它们整体的有效性,三个回归的Cragg-Donald Wald F统计量均有不同程度下降,不过依然显著。而在过度识别检验中,三个回归的检验结果均保持不显著。
综上,本文的工具变量是有效的,相应的工具变量估计结果也是可靠的。
(三) 稳健性检验
即使工具变量有效,本文的结果也可能是出于某种偶然因素,而并不真正反映因果关系,为缓解这种担心,本文做了如下稳健性检验。
首先,在表4所报告的回归中,本文分别用入学摸底考成绩和初三第一个学期期末考成绩代替小升初考试成绩与中考成绩来构建回归的核心解释变量和被解释变量。其中摸底考是在这些学生初一刚入学时进行,因而应该与小升初考试类似地,不太可能存在学生间的相互影响,更不太可能受其他同学、朋友此后考试成绩的影响;而初三第一学期期末考则与中考成绩类似,是同伴效应影响的结果。当然,这两次考试在受重视程度上不如小升初考试和中考,这可能导致其结果受偶然因素影响较大,因而只被用作稳健性检验。
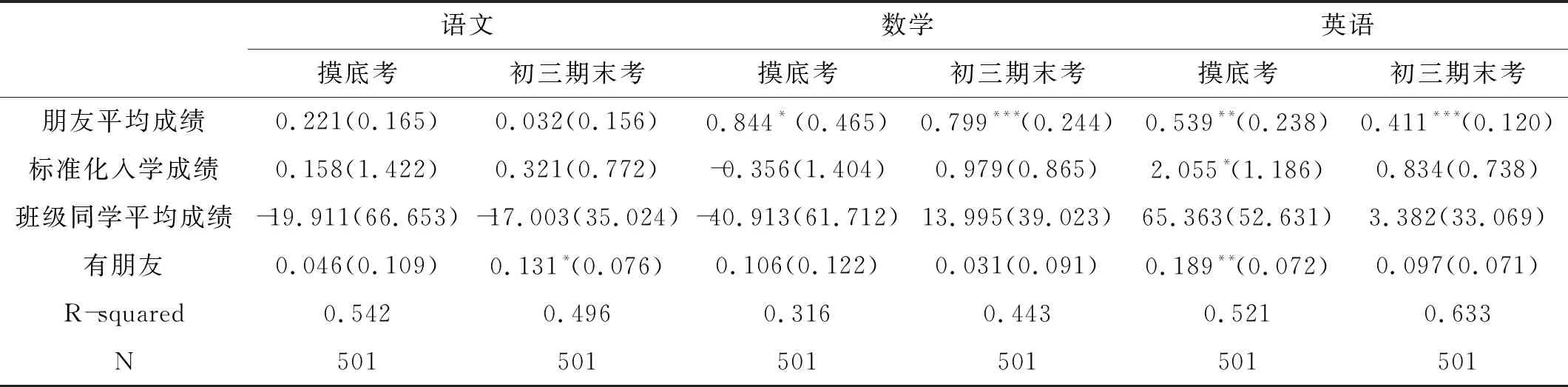
表4稳健性检验结果
表4的结果显示,无论是用入学摸底考代替小升初考试,还是用初三第一学期期末考代替中考,结果都没有发生显著变化:依然是在语文成绩上不存在显著的朋友间同伴效应,而在数学和英语上存在。这说明此前的结果,不太可能是源于一两次考试的偶然。
除了考试结果的偶然,表2的结果也可能出于朋友关系上的偶然,为缓解这一担心,本文尝试了先随机生成朋友关系,再看这些虚拟的朋友关系是否可以解释此前的结果。
为了让随机的朋友关系更能反映真实情况,提高这一检验的效力,本文按照学生的同班和同性别信息,分层进行了随机模拟。具体地,在本文样本中,同班且同性的潜在朋友组合共有4997种可能,其中真实的朋友关系有408对;同班不同性有5222种可能,真实朋友关系21对;同性不同班有57509种可能,真实朋友关系19对;样本中没有任何异性且不同班的朋友。类似地,本文也随机地生成408对同班同性朋友,21对同班不同性朋友,19对同性不同班朋友,然后再根据这一虚拟的朋友关系,分别生成各个解释变量,用以解释学生的中考成绩。逻辑上说,这些虚拟的朋友之间应该不存在真实影响,因而这些模拟回归的结果,应该是不显著的。相应地,如果这些结果与此前表2的结果差异不大,那就说明这个结果不需要用朋友间的相互影响来解释,相反,如果表2的结果显著异于随机模拟的结果,那这就可以被视为此前结果并非偶然的证据。考虑到这些朋友关系源于随机生成,应该不存在内生性,这些估计没使用工具变量法。

图3 随机朋友关系模拟结果注:图中所画的是基于1万次随机朋友关系模拟分别估计获得的朋友平均成绩变量系数t统计量的分布图。竖线代表表2中利用真实朋友关系所估计获得的朋友平均成绩变量系数t统计量。
这样的随机模拟一共进行了1万次,在每次模拟当中,本文都分别在语文、数学、英语这三门课上计算了朋友平均成绩变量的t统计量,一共获取1万个估计值。这些估计值的分布被分别画在了图3当中,作为对比,表2中基于真实朋友关系所计算获得的朋友平均成绩变量系数的t统计量估计值同样被用一条竖线表示在图3当中。显然,基于真实朋友关系所计算的数学和英语上的朋友平均成绩t统计量,都远大于利用虚拟朋友关系计算的t统计量。事实上,在数学和英语上,1万次模拟所获得的所有t统计量,都比真实统计量小。在语文上,真实值则落在了模拟值分布的期望值附近。这与表2的结论类似:朋友间在数学和英语成绩上存在显著影响,而在语文成绩上则不存在。
总而言之,稳健性检验,都说明表2的结果是稳健的,并非出于偶然。
(四)朋友影响的动态变化
逻辑上说,朋友之间的相互影响源于朝夕相处,需要以时间为前提。因而这一影响也可能会随时间发生变化。对这一变化的观测,既可以帮助理解同伴效应的产生过程,也可以作为一个反事实检验:学生在刚入学时的考试成绩,比如摸底考成绩,应该不会受朋友成绩影响,如果发现朋友成绩会显著影响摸底考成绩,那就很有可能存在其他被遗漏因素导致了朋友间成绩的相关性,从而使得表2的结果也需要被质疑。而反过来如果在朋友间在摸底考成绩上不存在相关性,则此前基于表2结果得到的结论:朋友间存在成绩上的同伴效应,其可靠性也会进一步增强(11)感谢匿名审稿人指出这一点。。
因而本文分别以中考为止的历次考试成绩作为被解释变量,估计了以入学成绩衡量的朋友平均成绩对学生历次考试成绩的影响,并将每个回归中朋友平均成绩的系数和95%置信区间报告在图4当中(12)笔者因故未能获得初一第一学期期末考试成绩,因而只估计了摸底考、4次期末考加上中考成绩6次考试的结果。。
图4的结果中,基于以历次语文成绩估计的朋友影响大小起伏不定,没有表现出清晰规律,且大多不显著。而以数学和英语成绩估计的朋友影响大小则表现出了共同的规律:开始时不显著,随后逐步变大,并在第四到第五个学期达到最高峰,随后趋于稳定。这一规律,反映了朝夕相处之下,朋友间影响的逐步增大,与理论预期一致,也从另一个角度佐证了本文的核心结论:朋友间在成绩上存在显著的相互影响。
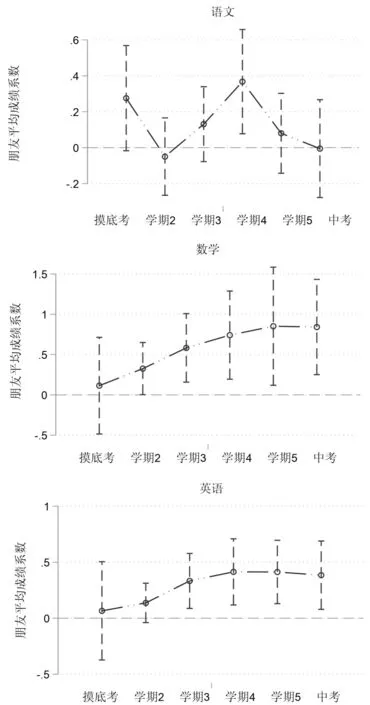
图4 基于历次考试成绩估计的朋友影响变化
(五) 异质性
本文到此为止的结果已足以说明朋友间同伴效应的存在性和重要性,不过,研究者可能还关心另一个问题:对不同群体而言,同伴效应有什么区别吗?或者说,同伴效应存在什么异质性吗?对此,本文主要从两个方面讨论了可能的异质性。
首先,在表5所报告的结果当中,所有学生被按照性别分成了两个子样本来分别进行回归。其结果显示,男生和女生间在同伴效应上的确存在一些区别。基于语文成绩所做的回归中依然不显著。在基于数学成绩所做的回归显示,男生受同伴效应的影响要轻微大于女生。在英语成绩回归中,女生回归的结果不显著,男生的结果则是显著大于零。

表5分性别回归结果
此前已有不少研究发现了不同性别学生在同伴效应上的差异[13, 20, 21],尤其是在数学内容较多的课程当中[33]。具体到本文结果在性别上的差异,它可能是因为不同性别学生在社交上的差异。比如有研究认为,女性更容易受朋友影响,这可能会带来女性间更大的同伴效应[34]。但它同样可能来自不同性别学生在不同课程学习能力上的差异。如表1所示,本文样本中不同性别间在各门课的成绩上均存在不小差异。它也可能来自于老师的影响。如前所述,样本班级21位相关任课老师里有20位是女性,且所有班主任都是女性。这或许同样会导致不同性别间学生在同伴效应大小上的差异。但限于数据,本文无法区分这些渠道。
表6所报告的回归则从另一方面进行了探索:所有学生被按照其入学成绩分成了较好的前1/2和较差的后1/2,并根据这一分类,分别进行了回归,从而讨论初始成绩不同是否会对同伴效应产生影响。
与表5相类似,表6的结果同样显示同伴效应在不同初始成绩的学生间存在显著差异。虽然语文成绩回归依然不显著,但无论是数学还是英语成绩回归均显示,初始成绩较好的学生,受同伴的正面影响都要大于初始成绩较差的学生。这个结果与Burke和Sass(2013)类似。在他们的研究中,最优秀的中学学生受同伴效应的正面影响也要远大于其他学生[32]。这或许是因为自身能力较强的学生,更有能力从优秀的朋友学到好的方面,从而提高自身的成绩。
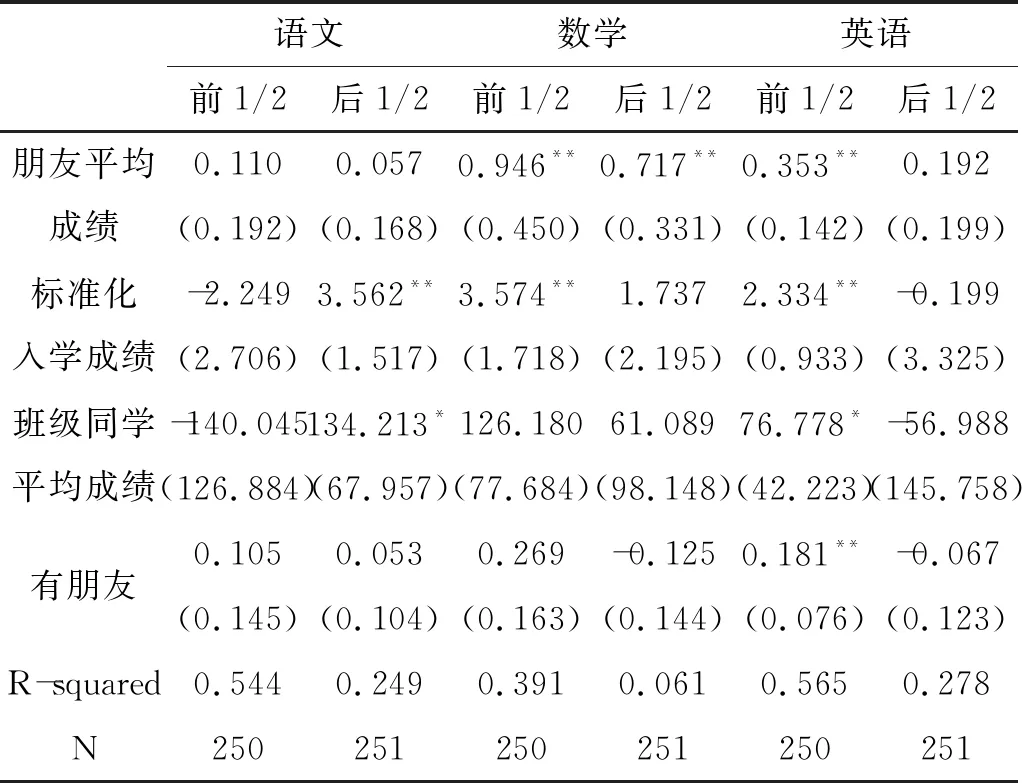
表6分入学成绩回归结果
考虑到优秀的学生其朋友的成绩本来就更好,这意味着同伴效应会扩大不同学生间在学习成绩上的差异,如果想实现“有教无类”的公平教育目标,那在同伴效应方面,或许也需要为较差的学生做点什么。
当然,本文在同伴效应异质性上的探索只是个初步的结果。由于数据上的缺陷,本文难以对此做更深入的分析。不过,本文的这些结果,至少可以为未来研究提供一个方向上的指引。
四、结论与启示
基于作者在浙江省一所非重点普通初中收集的数据,本文估计了初中生之间在语文、数学、外语三门课上的同伴效应。相比以往研究,本文特别关注了常为以往研究所忽视的真实朋友,而非普通同学之间的同伴效应。借助数据上的优势,本文实现了对同学间朋友关系网络的完整观测,并基于此实现了对朋友间同伴效应的识别与估计。
本文的估计结果表明,朋友之间在成绩上存在着显著的近朱者赤的相互影响:保持其他条件不变,朋友平均初始成绩更高的学生,其毕业时的成绩也会越高。此外,本文的估计还发现,朋友之间在成绩上的相互影响要远大于以往研究所关注的同班同学之间,而且这一影响在不同科目间、不同性别间、不同初始成绩的学生间都存在显著差异。
本文的结论意味着,当讨论同伴效应时,不能仅关注同班同学一类的表面上的同伴,而更要讨论学生真实朋友的质量。简单将一个差生分配到较好的班级,未必就能改善他真实的同伴质量,因而也未必就能改善他此后的成绩。
此外,本文的结论还意味着对一线的教学工作者和政策制订者来说,如果想利用同伴效应来影响学生的成绩,那不就能仅仅关注学生在不同群组间的分配,更要关注学生彼此之间的关系网络。

