基于深度多级残差网络的低信噪比下空频分组码识别方法

张聿远，张立民，闫文君

（海军航空大学信息融合研究所，山东烟台 264001）

1 引言

在非协作通信情况下，从接收信号中对发射机通信信号类型进行识别，是通信侦查和软件无线电领域的一个重要研究课题.随着频谱资源的短缺，多输入多输出系统（Multiple Input Multiple Output，MIMO）与正交频分复用（Orthogonal Frequency Division Multiplexing，OFDM）技术的结合因其频带利用率高和抗多径干扰能力强的优势，得到了越来越广泛的应用［1］.在实际通信过程中，信号往往需要在低信噪比的复杂电磁环境中传输，信号受噪声和信道衰减的影响较大，因此，如何从强干扰环境中正确识别发射机信号类型亟待解决.

现有的空频分组码（Space-Frequency Block Coding，SFBC）识别方法较少，且以人工提取特征的传统算法为主，通常采用在分析信号统计特性后，建立决策树并逐项进行假设检验以完成识别［2～6］.基于中心极限定理，文献［2］提出了一种基于二维空间-频域冗余（Two-Dimensional Space-Frequency Redundancy，TDSFR）的SFBC 识别算法，利用空域冗余构造估计量的互相关函数，在假设检验统计量中加入频域冗余以实现识别；文献［3］提出了一种基于子空间分解（Subspace Decomposition，SD）和随机矩阵理论（Random Matrix Theory，RMT）的SFBC 盲识别方法，根据噪声子空间的最大特征值确定决策边界，然后利用一个特殊距离度量的决策树进行决策；文献［4］通过计算互相关函数峰值以识别AL-OFDM 码，对SM 码有较强的识别能力；文献［5］利用主成分序列（Principal Component Sequence，PCS）作为识别特征，通过在频域内滑动窗口检测该特征以实现空频分组码识别；文献［6］基于中心极限定理（Central Limit Theorem，CLT），利用空间域冗余计算估计量的互相关函数，构造卡方统计量作为识别决策量.以上这些方法［2～6］均为人工提取特征的传统算法，其性能依赖于专业知识和经验，而且提取的都是浅层特征.因此，如何自动提取SFBC的深层特征，提升算法在低信噪比下的识别性能成为了本领域具有挑战性的问题.

为解决上述问题，本文提出了一种基于时频分析与深度多级残差网络［7］（Deep Multilevel Residual Network，DMRN）的SFBC 自动分类识别系统，可自动获取SFBC的深层特征，提升识别精度.该系统由3 部分组成：SFBC 互相关序列时频分析与降噪、非时钟同步预处理和基于多级残差的深度SFBC识别网络.首先对接收端互相关幅值序列进行时频分析得到二维时频图像，并采用叠加均值的方法进行时频域降噪以稳定AL-OFDM码峰值；然后，通过非时钟同步拼接的方法，确保在任何时延情况下总有一组特征靠近图片中心，解决了不同时延下识别性能不稳定的问题；最后针对时频图像特征细微的问题，设计了一种适用于SFBC识别的DMRN模型，使得浅层网络的细节信息和深层网络映射的高维特征能够充分融合，显著提升了低信噪比下的识别性能.

2 空频分组码模型及其特性分析

空频分组码将空间编码（Space Block Coding，SBC）与OFDM 技术相结合，使得信号在充分利用空间资源的同时，进一步挖掘可传输的频谱资源，有效地扩大了信道的信息容量，其实现过程主要包括SBC 编码与IFFT两步，MIMO-OFDM发射机模型如图1所示［1］.

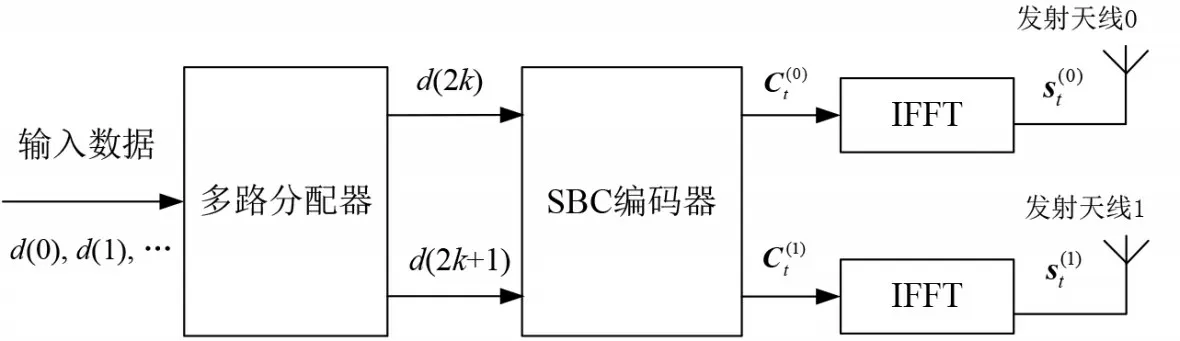
图1 MIMO-OFDM发射机框图

考虑利用两根发射天线（nt=2）的MIMO 系统，待编码的数据流首先通过多路分配器分解成两路子数据流，然后输入SBC 编码器实现SM（Special Multiplexing）或AL（Alamouti）编码.SM码和AL码的编码矩阵为

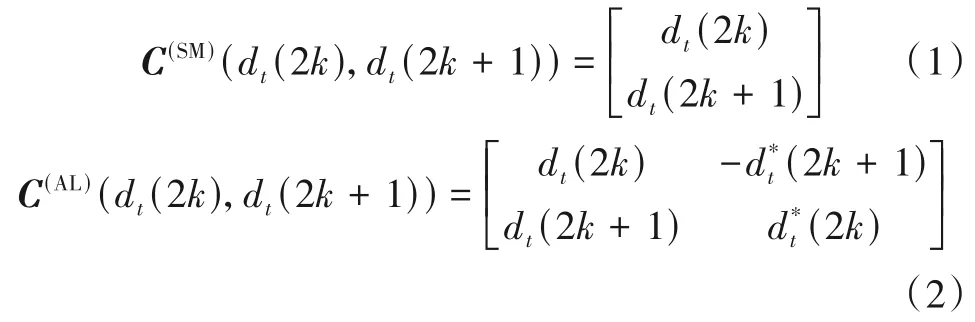
其中，dt(2k)和dt(2k+1)分别表示数据集dt中的第2k列和第2k+1 列数据.经过编码后数据集dt由1×2N维变为Nt×UN，其中对于SM 码U=，对于AL 码U=1.将编码后两路数据分别表示，即然后进行IFFT 以生成OFDM符号.

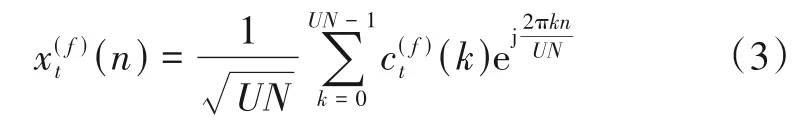
其中，n=0，1，…，UN-1，f=0，1代表发射OFDM 符号的天线编号.最终经由两根发射天线传输的信号为

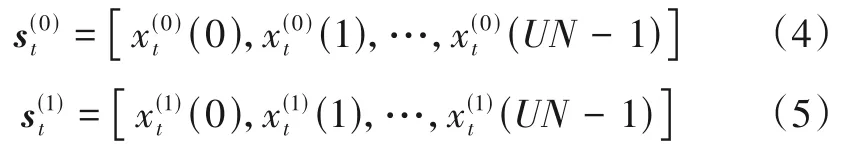
考虑利用nt根发射天线和nr根接收天线的MIMOOFDM 系统，则接收端第v根天线的第m个接收信号可表示为

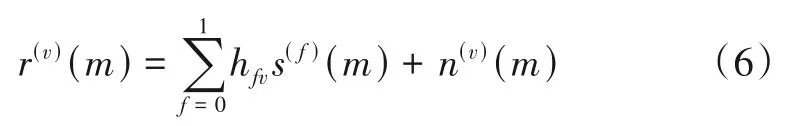
其中，hfv为发射天线f与接收天线v之间的信道系数，n(v)(m)代表加性高斯白噪声，s(f)(m)为天线发射f的发出的第m个信号，v=0，1，…，nr-1.本文考虑在SFBC中最常用的SM与AL两种编码方式［4］.

计算两根接收天线信号之间的二阶互相关函数，可得到空频分组码的互相关特性.不失一般性，考虑nr=2的MIMO-OFDM系统.定义如下的二阶互相关函数：

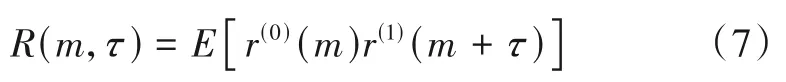
其中，E[·]为数学期望，τ为互相关函数的时延.考虑互相关序列y=[y(0)，y(1)，…，y(m)，…，y(K-1)]，其中y(m)=r(0)(m)r(1)(m+)，对该序列进行DFT 可得到频域互相关序列：

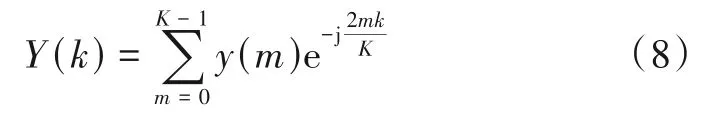
其中，k=0，1，…，K-1.对于SM 码，根据式（1）和式（3）～（7），由于传输的数据符号是独立同分布的，容易得到

对于AL 码，在同一个编码矩阵内，由于(k0)和(k1)相互交叉的两项具有相关性，其余各项均不相关，易知AL码频域互相关序列Y(AL)存在峰值.

3 时频域特征降噪及预处理

3.1 SFBC互相关特征与时频域降噪

现有的空频分组码识别均采用传统的假设检验方法［2～6］，未见深度学习算法在该领域的应用，为探索一种适用于SFBC 的特征预处理方法，本文借鉴了雷达辐射源识别领域中常用的CWD 时频变换［8～11］，对SFBC 互相关序列进行时频分析，解决了一维序列峰值稀疏，直接输入神经网络识别性能差的问题.

考虑到在计算机视觉领域（Computer Version，CV），输入层的图片维度常采用边长相同的方形结构，且边长往往取2的幂次方，故将已转换到频域的互相关序列Y按照OFDM 块的长度N进行划分，每N块OFDM符号按行排列成一张图片，则图像的第k+1 行可表示为

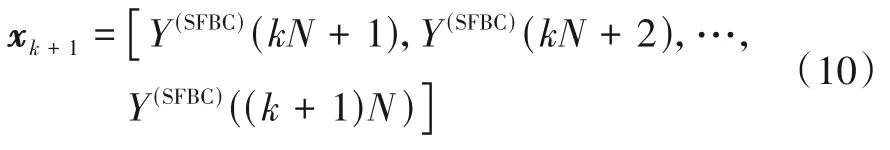
其中，SFBC ∈{SM，AL}表示SFBC 类型，k=0，1，…，N-1.则时频图像可由N行序列xk+1拼接而成.

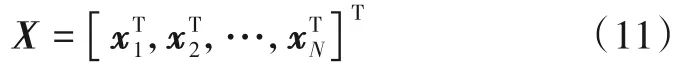
以OFDM 块长度N=64 为例，得到10 dB 下N×N维的时频图像如图2所示.由该图可知，AL-OFDM码的互相关时频图像存在周期性的峰值，且峰值恰好排列在第一个子载波的位置，而SM-OFDM 码则不存在此类峰值.该方法使得信号的特征更加集中，有效提高了峰值特征的密集程度.

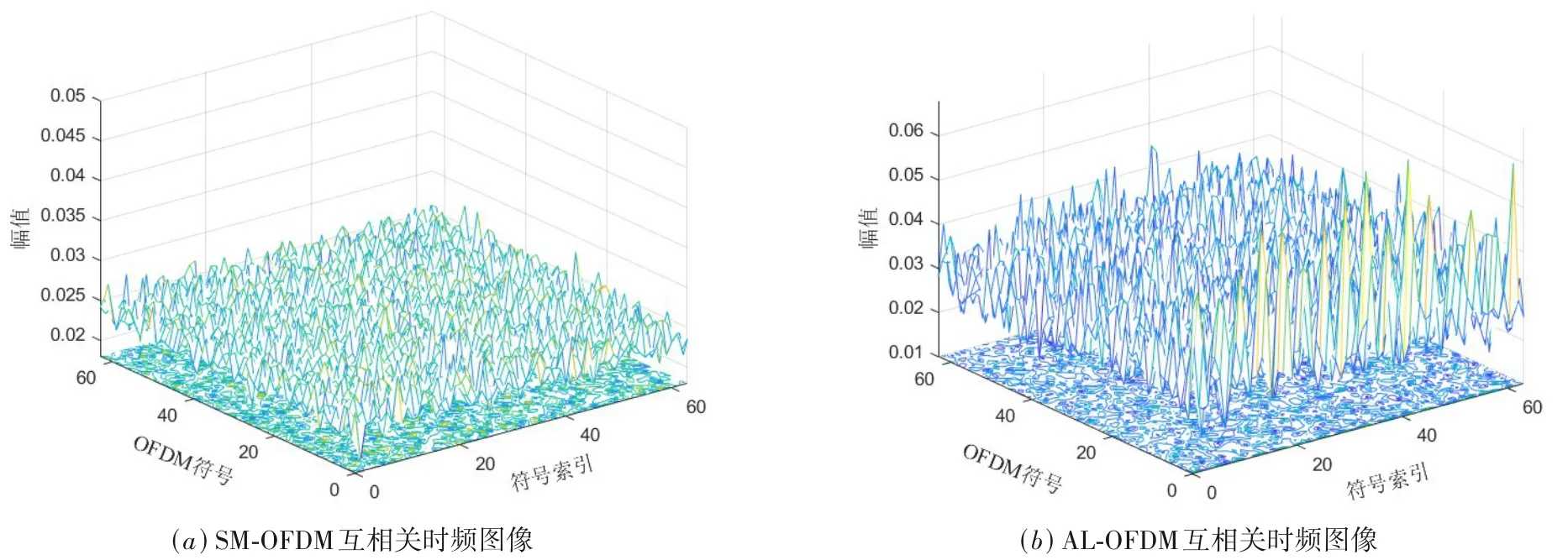
图2 SFBC信号互相关时频图像

由图2（b）可知，AL-OFDM 码的峰值存在较大波动，在低信噪比下该特征更加难以显现，导致识别性能较差.考虑到该峰值呈周期性排列，且顺序提取的互相关序列经时频分析后特征位置不变，本文利用该性质特点，将多张时频图像叠加以提升抗噪性能.此外，将64 块OFDM 块作为一个样本时，采集的信号数仍较文献［4］更少，因此本文对SFBC 互相关时频图像进行均值叠加处理.

其中，Ns为叠加的时频图像数.由于峰值的波动具有随机性，将多张时频图像叠加可以稳定AL-OFDM 互相关峰值，达到削弱噪声干扰，提升特征可辨识程度的目的.

3.2 非时钟同步拼接

在实际的通信系统中，接收端的第一个信号可能不是发射端OFDM 块的第一个子载波，在这种非时钟同步（Non-Clock Synchronization，NCS）的情况下，时频图像的峰值会发生明显的偏移，导致神经网络模型对SFBC 的识别性能不稳定.此外，根据卷积神经网络（Convolutional Nerual Network，CNN）的工作原理，接近图像中心的特征在卷积核移动时能够被其多次利用，而边缘化的特征则利用率较低.针对以上问题，本文提出了一种在各种时延下均适用的预处理方法——拼接，将两张时频图像进行非时钟同步拼接（Non-Clock Synchronous Splicing，NCSP）处理.

其中，和分别表示去噪后第2i个和第2i+1 个时频图像.采用按列拼接的方式，则预处理后时钟同步（时延t=0）与不同步（以时延t=16，32，48 为例）下的时频图像如图3所示.

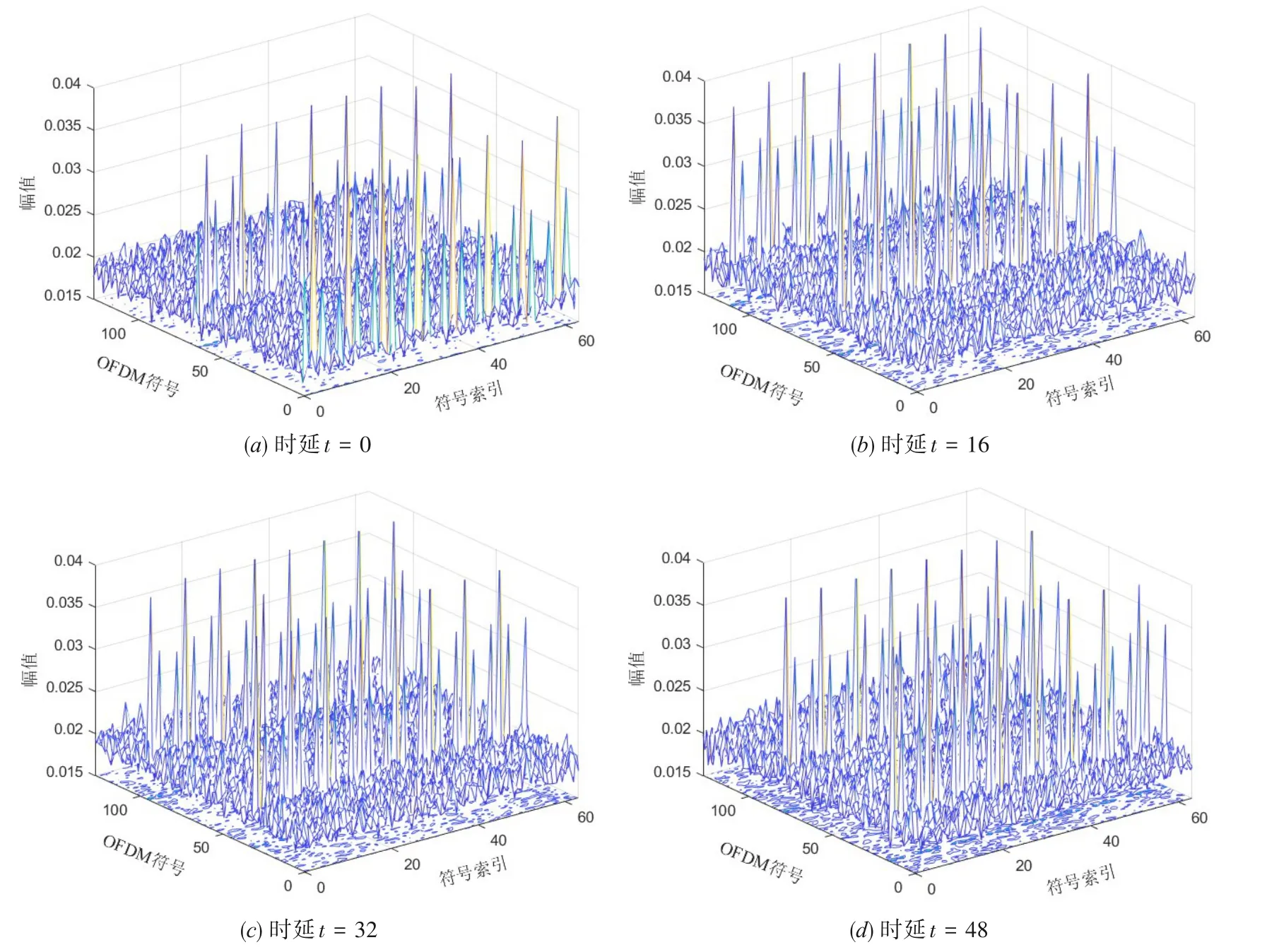
图3 预处理后的AL-OFDM码互相关时频图像

如图3（a）所示，在时钟同步（时延t=0）的情况下，时频图像的一组峰值在OFDM 符号的第一个子载波的位置（第1 列），另一组峰值则恰好在图像的中心（第65列）.同理，如图3（b）～（d）所示，在时钟不同步（时延t=16，32，48）的情况下，因两组峰值的列数之差恰好等于OFDM 块长度N，当其中一组子载波的峰值在图片边缘时，另一组峰值则必然在接近图片中心的位置.该拼接方法使得时频图像总有一组峰值靠近中心，更利于卷积核提取互相关特征.

4 基于多级残差网络的空频分组码识别系统

4.1 多级残差单元

CNN在图像识别领域取得了突破性进展.理论上，更多的卷积层可以拟合任意复杂的非线性函数，但实际上，随着网络层数的增加，其识别性能会达到饱和甚至发生退化.文献［12］提出了一种解决网络退化问题的残差网络（Residual Network，ResNet），每个残差单元（Residual Unit，RU）的输出可表示为

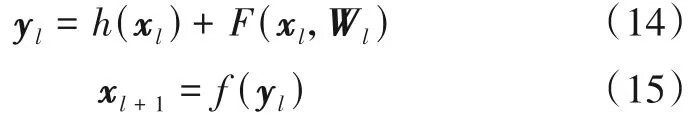
其中，xl和xl+1分别为第l个残差块的输入和输出，F为残差映射函数，h为跨越连接的映射函数，在恒等映射下h(xl)=xl，f为线性整流（Rectified Linear Unit，ReLU）激活函数.

跨越连接使得ResNet 能够利用多层的映射特征，但本文的SFBC 互相关时频图像的峰值特征较为细微，仅使用一层跨越连接仍会因浅层特征丢失，导致细微特征被忽略.尤其是在低信噪比下，信号受噪声的干扰较大，AL-OFDM 信号时频图像特征不明显，使得互相关峰值“湮没”在噪声中.因此，本文在在单一跨越连接的基础上分层增加跨越连接，构成多级残差单元（Multilevel Residual Unit，MRU），在不增加模型空间复杂度的条件下，改善ResNet 网络的深层优化能力，其结构如图4所示.

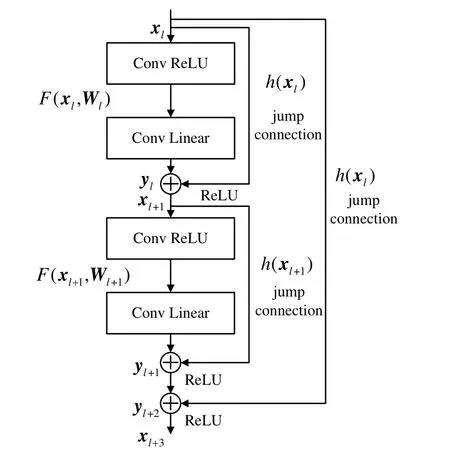
图4 多级残差单元结构示意图

在图4中，前两层和后两层卷积在增加跨越连接后分别构成两个一级残差单元，2个一级残差单元和跨越连接h(xl)构成二级残差单元.设第l个二级残差单元的输入为xl，则各残差单元的输出为

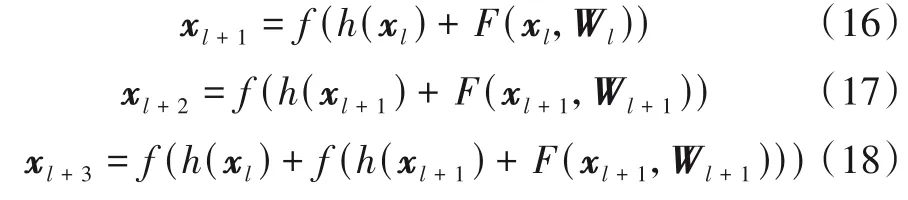
从输出xl+3可分析出，多级残差单元的输出不仅包含映射函数F(xl+1，Wl+1)，而且融合了本级和上一级残差块的输入xl+1和xl.因此，多级残差能够充分利用跨越多层的特征信息，融合浅层网络的细节信息和深层网络映射的高维特征，使网络的结构更加紧凑.

4.2 基于深度多级残差的SFBC识别网络

一般残差网络输入图像的维度较大，且图像特征分布较广，不利于提取SFBC 时频图像的细微特性.为适应输入图像维度较小和特征细微的特点，本文在文献［12］基础上进行了如下改进：网络的主干部分如图5所示，原网络仅有一个池化层，本文在每两个二级残差单元之间增加池化层，实现对图片快速降维的同时保留峰值特征信息，设Gi(x)为第i个网络层的输出，则残差-池化网络部分的输出为

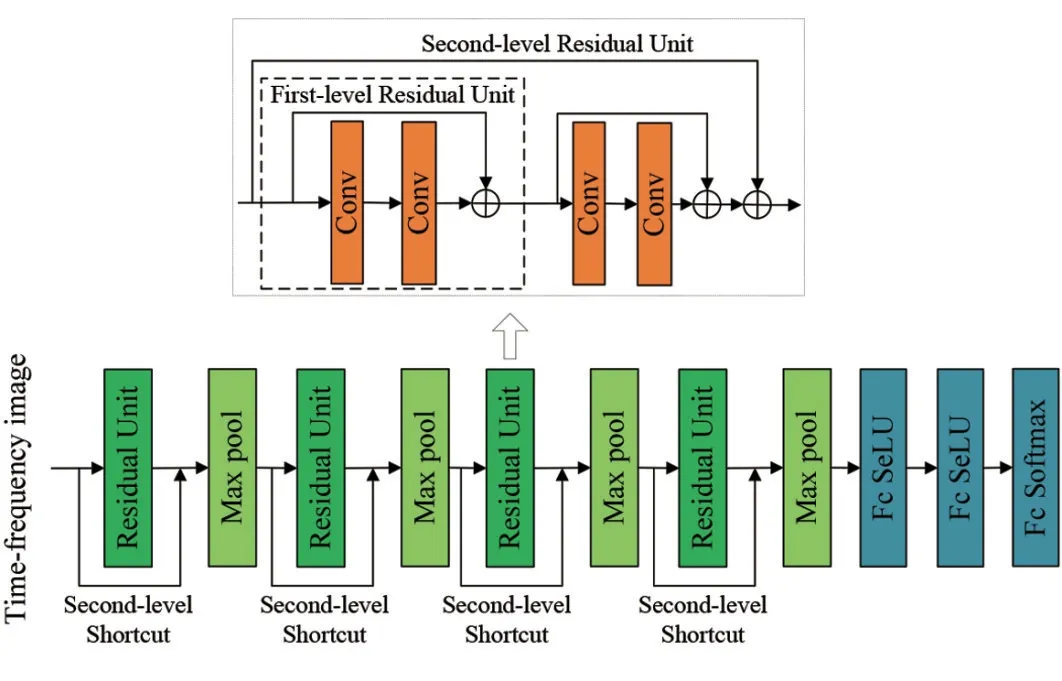
图5 DMRN网络结构示意图

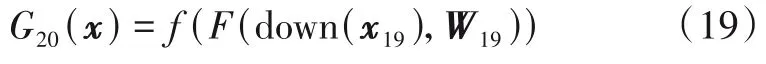
其中，down(·)为池化函数.此外，本文采用最大池化代替原网络的平均池化，以最大限度保留初始的互相关峰值特征.考虑到输出层的分类类别较少，故将原有的1层全连接改为3 层，防止因权值参数减少过快而导致信息丢失.

由于文献［12］中图片的输入维度为224×224，与本文互相关时频图像的输入维度不同，因此将输入层的维度设计为64×128，以适应SFBC 信号预处理图像的输入维度.此外，为将SFBC 时频图像压缩成适合神经网络处理的方形结构，除第一个池化层的步长设置为（1，2）以外，其余各层均为（1，1）.

考虑到该互相关时频图像不同于一般的视觉图片，其特征为两条平行排列的峰值，且分布较为稀疏，为了充分利用该峰值按列平行分布的特点，提高识别性能，本文将基本残差单元中的卷积核大小设置为4×8，通过增加横向维度提高峰值的利用率，使得卷积核在更多步内能提取到图像特征，网络各层的具体参数设置如表1所示.

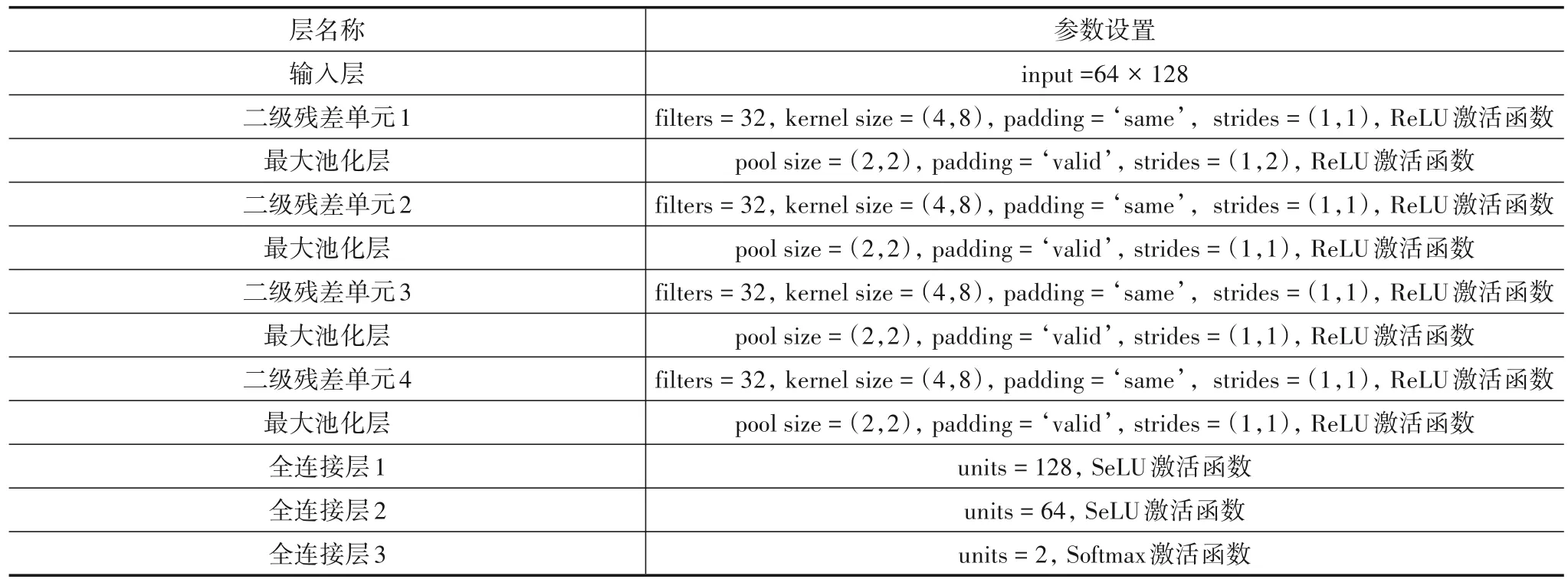
表1 DMRN网络参数设置

4.3 基于DMRN的空频分组码识别

基于DMRN的空频分组码识别系统如图6所示，算法的实现步骤为：（1）在已在SFBC类型下，对互相关幅值序列进行时频域降噪及预处理，获取互相关时频图像；（2）将时频图像x与类型标签y对应连接作为训练样本；（3）将带标签的样本输入网络，通过监督训练得到DMRN模型参数；（4）测试样本经过相同预处理后送至训练好的DMRN模型进行识别验证，采用无监督方式完成测试过程.

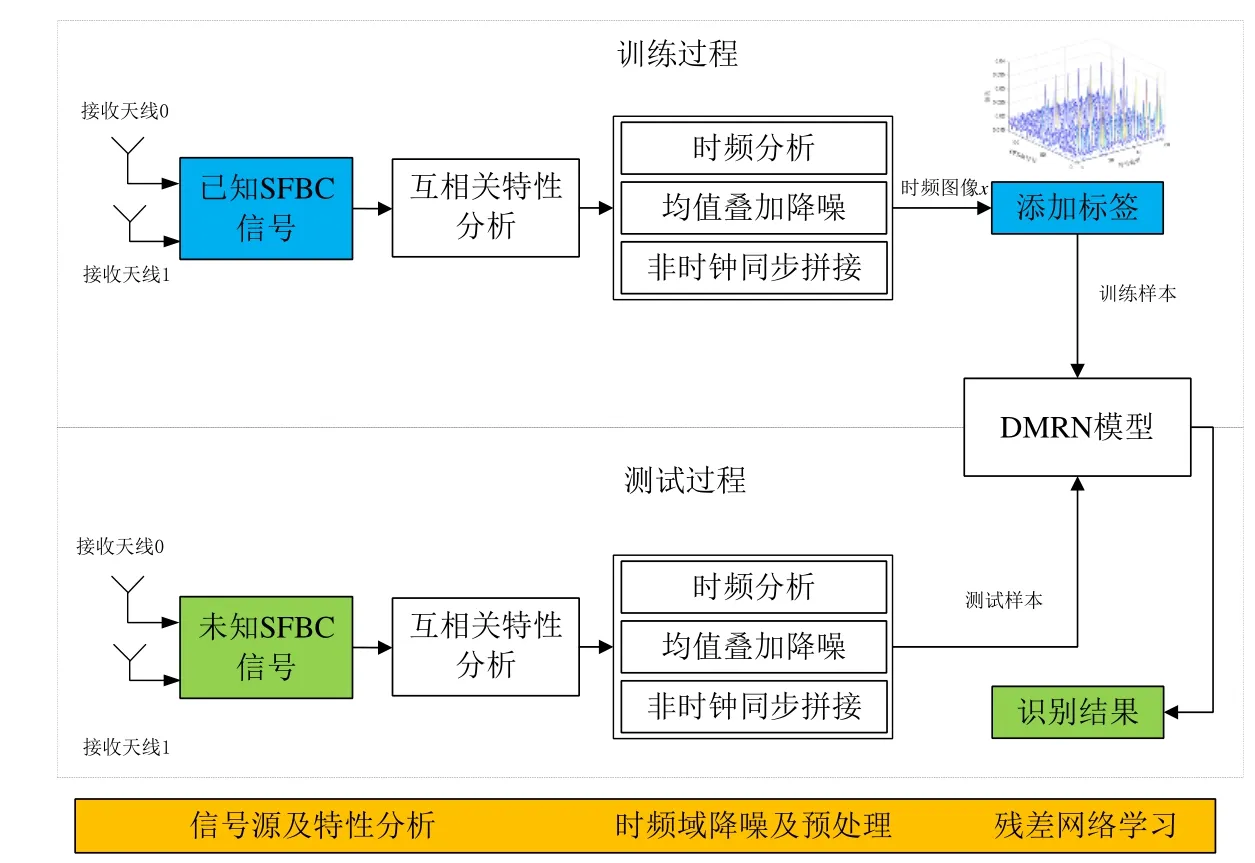
图6 基于DMRN的空频分组码识别系统

5 实验结果与分析

5.1 样本生成及实验环境

仿真信号选取OFDM 块的子载波数N=64，每个样本所需的OFDM 块数为Nb=128，调制方式为QPSK.仿真信道采用频率选择信道，包含Lh=3 条独立路径，将每一个信道抽头建模为独立复高斯随机变量，其功率服从指数PDF，接收天线数nr=2.信噪比范围为-15～10 dB（步长1 dB），在每个信噪比下单类SFBC产生100 个样本，总样本容量为4200，训练集占总样本的50%，其余50%为测试集.

模型的训练和测试在Intel（R）Core（TM）i7-9700 CPU 和16GB 内存的环境下进行，并使用支持CUDA 环境的NVIDIA GeForce RTX 2080 Ti GPU 对训练过程进行加速，数据集采用Matlab 软件仿真产生并进行预处理.在网络优化过程中，本文采用Adam 优化器进行最优值求解，并选取交叉熵作为损失函数.

5.2 算法识别性能分析

5.2.1 预处理效果分析

图7为叠加时频图像数Ns∈[10，40]及未降噪条件下识别性能随信噪比的变化图像.对比不同叠加图像数曲线可以得出：识别性能随信噪比呈递增趋势，高信噪比时趋于稳定.叠加的时频图像数越多，均值叠加处理获取的信噪比改善增益越高，性能改善明显.叠加图像数Ns增加到20 后性能提升有限，且带来额外的数据集开销，因此本文选取Ns=20进行时频域降噪处理.

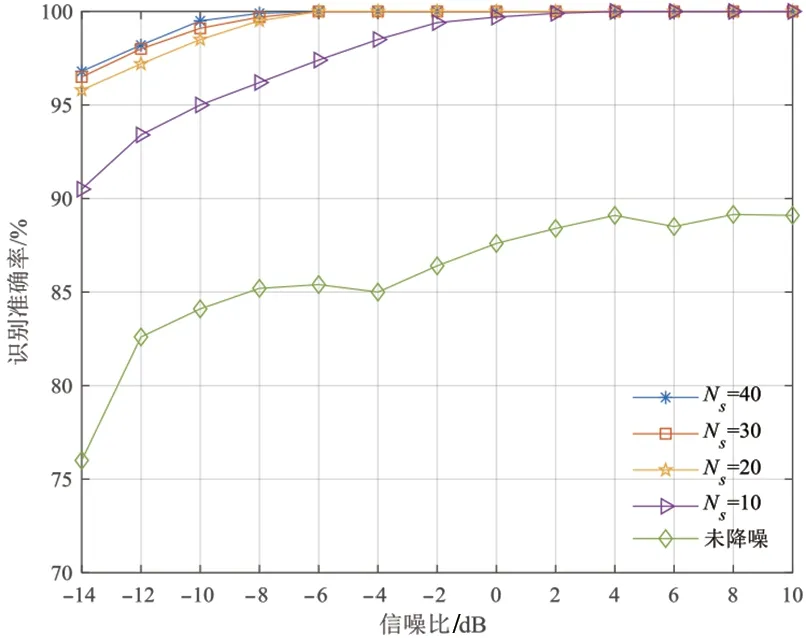
图7 不同叠加图像数对的识别性能的影响

为验证非时钟同步拼接的有效性，在时钟同步（时延t=0）和不同步（以接收端时延等于OFDM 子载波长度的1/4、1/2为例）的情况下，对拼接前后的识别性能进行实验，结果如图8 所示.经分析可知：（1）拼接处理后算法在3种时延条件下识别性能提升较大，低信噪比下明显优于未处理的情况，在-10dB 时准确率均达到了98%以上；（2）时延t=32 在拼接前后的性能均略优于其余2种情况，这是由于该时延下的时频图像峰值处于靠中心位置，可提取到峰值特征的有效区域更大；（3）时钟同步条件下，未拼接处理的识别性能较差，原因在于其峰值特征边缘化严重，NCSP 处理后性能明显改善.NCSP 处理可确保不同时延下总有中心化的峰值特征，因而有效解决了非时钟同步下的识别问题.

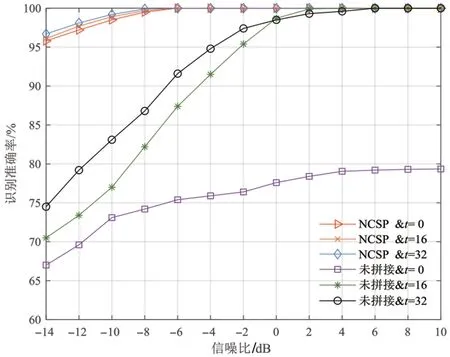
图8 不同预处理与接收端时延下的识别准确率

5.2.2 不同样本下的识别性能分析

为进一步分析非时钟同步拼接带来的额外样本开销，在总信号数相同的条件下进行实验，NCSP 训练样本数S设置为未拼接处理的1/2，识别结果如图9 所示.从图中可以得出：（1）在NCSP 和未拼接情况下，识别性能均随样本数增加而逐渐上升，且提升幅度随样本数增加逐渐趋于饱和；（2）在相同信号数下，除S=40 外，NCSP 较未拼接的性能均更优，说明拼接操作虽使单个样本的信号数增加了一倍，但在相同信号数下的性能仍取得了有效提升，在相同开销下改善了低信噪比下的特征辨识能力；（3）在样本数适中时，NCSP 较信号数相同的未拼接处理性能提升最明显，在NCSP 样本数为80，未拼接处理样本数为160 时，-14dB 下的识别增益达到了10.6%.原因在于样本数较少时网络无法充分收敛，而过多样本数使得增益趋于饱和.在总信号数开销相同的情况下，NCSP 仍获得了更优的识别性能，从而验证了非时钟同步拼接的有效性.

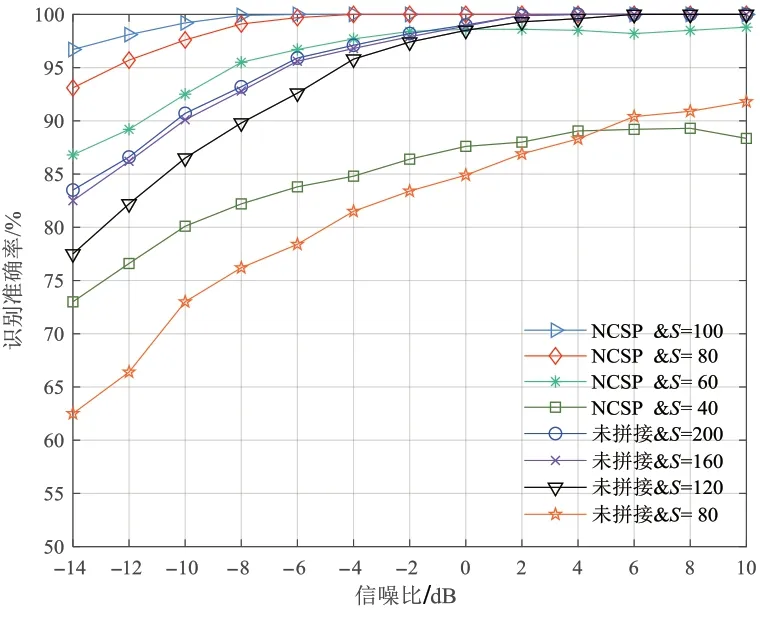
图9 不同样本数下的识别准确率

5.3 基于DMRN的空频分组码识别

由于现有的空频分组码识别算法较少，且均为人工提取特征的传统算法，为验证DMRN 模型在低信噪比下的性能优势，本节选择如下4种方法进行对比：（1）TDSFR［2］；（2）SD+RMT［3］；（3）PCS［5］；（4）CLT［6］.以上文献［2，3，5，6］均为基于假设检验和统计特征量，利用决策树和人工阈值判断空频分组码类型的典型传统算法，本文方法与以上4种方法的识别准确率如图10所示.

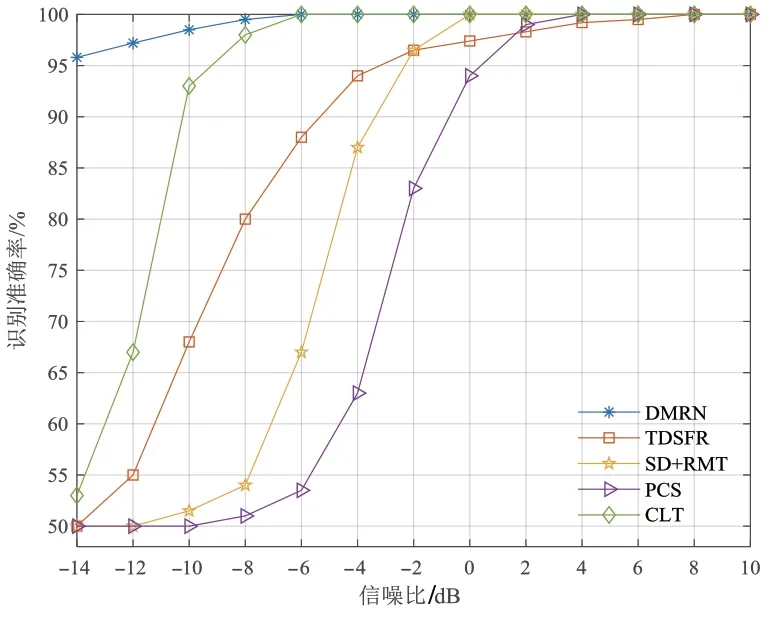
图10 不同算法的识别准确率对比

从图中可以看出，得益于深度学习模型对标签数据的自学习能力，本文方法在-10 dB下的识别准确率达到了98.5%，低信噪比下较基于假设检验的传统算法性能提升明显，具有更强的深层特征映射能力.传统算法的识别性能很大程度上取决于人为设定的阈值，在进行假设检验的过程中，人工设定参数对复杂环境的适应性较差，提取的累积特征量可能存在较大波动.而本文设计的基于多级残差网络的深度学习模型，通过对预处理的时频图像进行深层解析，规避了传统算法中人工设计阈值，在低信噪比下识别性能较差的问题.

5.4 不同网络识别性能对比

为验证本文设计的DMRN 能够获得更优的识别性能，本节将DMRN 模型与当前在图像识别领域表现优异的深度学习模型CNN［13～15］和ResNet［16］进行对比.测试的三种网络模型具有相同的输入层、卷积层、池化层和全连接层，各层的参数设置均一致，区别在于ResNet 在CNN 基础上增加了跨越连接，DMRN 利用ResNet 的2 个子残差块构成二级残差单元，三种模型在-8 dB、-10 dB、-12 dB和-14 dB下的混淆矩阵如图11所示.

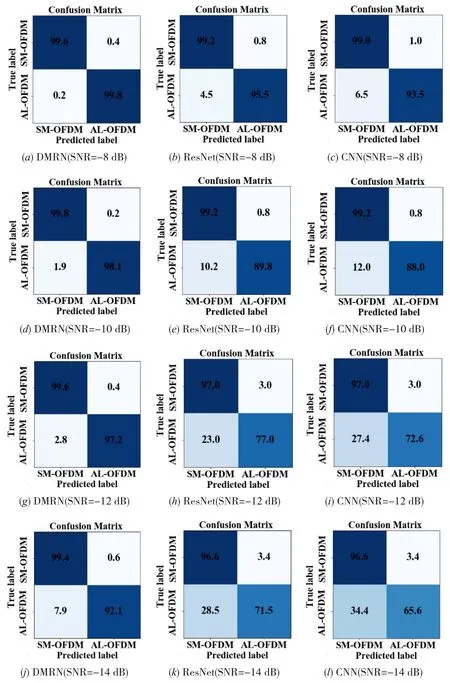
图11 不同网络在低信噪比下的混淆矩阵

由图11 可知，SM-OFDM 码的识别准确率更高，其时频图像不存在互相关峰值，不易被判别成AL-OFDM码；低信噪比下AL-OFDM 码的特征较为微弱，使得其细微差异被噪声进一步削弱.此外，DMRN 模型在-14 dB 下的整体识别准确率达到95.8%，较ResNet和CNN 分别高出14.4 个百分点和17.4 个百分点.由此验证了DMRN 模型在SFBC 识别中的优势：添加多级跳线连接以利用跨越多层的映射特征，使得浅层细节信息和深层高维特征能够充分融合，更利于网络对时频图像特征信息的提取，从而获得更优的识别性能.

表2 为不同模型的复杂度比较，由于三种模型的参数设置一致，故网络模型的待训练参数量均为599，874，空间复杂度相同.时间复杂度由训练迭代耗时和识别耗时两方面分析，训练迭代耗时为迭代100轮的统计平均，识别耗时为单个样本完成识别的时间.对比表中数据可以得出：ResNet 和CNN 的训练耗时比DMRN 较少，但基本上相差不大；得益于GPU 并行运算能力的提升，三种网络对单个样本的识别时间均处于ms 数量级，具有较强的实时性.综合对比识别性能与计算复杂度，本文的DMRN 模型在识别准确率和效率上的综合性能更优.

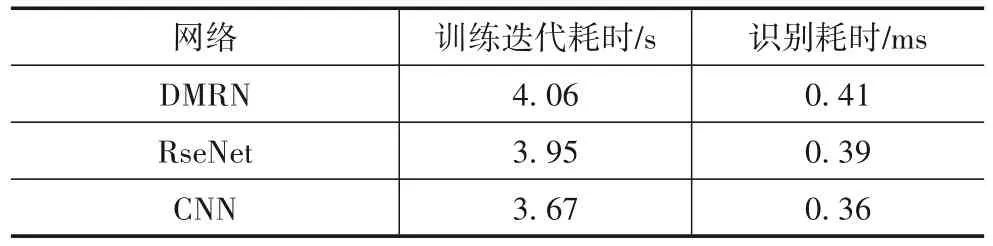
表2 网络复杂度分析

6 结论

本文结合深度学习技术优势，提出了一种基于时频分析与深度多级残差网络的空频分组码自动识别系统，有效地解决了低信噪比下识别困难的问题.该系统利用时频分析进行特征聚合与维度变换，解决了一维互相关特征稀疏，直接输入网络识别性能较差的问题；非时钟同步拼接克服了峰值波动较大和非时钟同步敏感带来的不稳定性，在相同样本开销下获得了更优的识别性能.相对于其他文献所提及的神经网络，深度多级残差网络具有更强的学习表征能力，能够融合跨越多层的高维和低维映射特征，具有更优的综合识别性能.由于本文提出的方法自动提取特征，不仅解决了传统算法人工提取特征困难的问题，并且在低信噪比下显著提升了算法的识别性能，为低信噪比下空频分组码识别提供了一种新的可行方案.