基于四维混沌理论和多方向扩散的彩色图像加密

贾晓霞，杨玉丽

(1.太原学院 计算机科学与技术系，山西 太原 030000;2.太原理工大学 信息与计算机学院，山西 太原 030024)

近些年，随着科技的迅猛发展，在表达和分享敏感信息时，数字视频图像得到越来越多的使用[1]。如何高效地进行图像数据交流和分享一直是信息安全领域的研究热点，保证图像安全性的常用手段是图像加密[2]，在实际使用中，图像加密技术必须保证安全、高效、快速等机制。

与其他形式的信息不同，图像邻近像素的信息相关性非常高，传统加密方案，例如:数据加密标准(Data Encryption Standard，DES)、国际数据加密算法(Internationale Data Encrypt Algorithm，IDEA)、高级加密标准(Advanced Encryption Standard，AES)，难以保持较高标准的安全性[3，4]。基于混沌映射和混沌系统的加密方案[5]的优点有:对初始值和其他系统参数的高敏感性、明文敏感性、密钥空间大、混沌性和遍历性等，但很多加密方案不能抵御经典攻击。

因此，很多研究者对图像加密进行了改进和完善，如Mao等[6]提出基于动态密钥选择与多方向扩散的图像加密算法。利用128位外部密钥来生成4个Logistic映射的初值，并设计了4方向连续扩散方法对置乱图像进行加密，该方案对抗明文攻击能力显著。ELAMIR等[7]提出的图像加密密钥由混沌映射和DNA计算编码规则组合而成，实验表明该方法可以抵御多种常见攻击，但总体计算成本较高。Chen等[8]基于rand函数生成随机转换规则，但问题在于其与明文图像无关。不同的明文图像有着相同的转换规则，因此该方案不能抵御明文攻击、选择明文攻击和统计攻击。Askar等[9]提出了一种新的离散分数阶食物链模型，在此基础上，提出了一种基于模型混沌行为和椭圆曲线密钥交换的混合加密方案。Niu等[10]改进了约瑟夫遍历问题，并将其与DNA编码技术结合应用到图像加密中，该方法具有强密钥敏感性，可抵御多种常见的攻击，但密文图像不能很好关联到明文图像和密钥流，因此该方案不能抵御明文攻击。Cheng等[11]提出了基于混沌Gyrator变换与矩阵分解的非对称彩色图像加密算法。该方法可有效抗击明文攻击，但未明确对密文攻击的有效性。

为此，需要开发高效稳健的安全加密方案，以克服上述问题。为克服低维混沌映射的缺点，本文采用四维混沌动力系统。为降低混沌数据的大小和计算成本，利用混沌动力状态变量选择程序，从混沌动力系统的迭代生成的相同混沌数据上生成多个密钥流;本文根据密钥流，设计了四个不同的扩散方向，像素的RGB值通过不同方向的扩散机制来增加密文随机性，从而增强密文抗攻击的能力。

1 混沌逻辑理论

1.1 四维混沌系统

在混沌系统[12]的应用中，生成随机数据的常用方法包括Baker映射、Lorenz映射和logistic映射等。本文选择使用混沌tent映射[13]，其定义如下

(1)

式中:a∈(0，ρ)为整数，「·⎤表示向上取整，⎣·」表示向下取整。

为了生成带期望属性的混沌数据，一般利用混动动力系统。在众多混沌动力系统中，四维混沌动力系统(Chaotic dynamical system，CDS)更佳，且更为完善。采用四维混沌动力系统，可以克服低维混沌映射系统的缺点。其定义如下

(2)

该新系统具有对称性和耗散性，且包含非常丰富的动力结构。a、b、c、d、b1、b2、b3和b4为CDS参数值。x1、x2、x3和x4表示4个不同维度的数值。

1.2 混沌动力状态变量选择程序

为降低计算成本，降低了混沌数据的大小，利用混沌动力状态变量选择程序[14](Chaotic dynamic state variable selection program，CDSVSP)，从混沌动力系统迭代生成的相同混沌数据上生成多个密钥流，下面简单介绍CDSVSP。

取8位像素值的一维数组(大小为M×N):P={P(0)，P(1)，P(2)，…，P(MN-1)}，其中，M和N为明文图像维数。对于初始值x0、y0、z0和w0，将式(2)迭代(M×N)/4+n0次，n0≥0，这些初始值将作为密钥的一部分。本文借助以下定义解释CDSVSP。

(1)首先利用CDS(式2)的每次迭代，得到4个状态变量X、Y、Z和W的数值。设S={Xi，Yj，Zk，Wl}，其中，Xi、Yj、Zk、Wl分别为X、Y、Z、W在第i、j、k、l次迭代中的状态，且i、j、k、l的数值彼此间不相等。

(2)将新变量slt(L)定义为在{Xi，Yj，Zk，Wl}中选择的变量

(3)

利用该变量，生成P(L)的密钥流元素。基于指标index(L)作出决策，定义为

index(L)=mod(f(a，ρ，P(L-1))，4)

(4)

式中:f(a，ρ，x)为tent映射。a和ρ参与到密钥构建。对于第一个像素值，P(-1)设为种子值。

CDSVSP的工作原理如下。

选择足够大且彼此不同的i0、j0、k0、l0作为密钥。为第一个像素P(0)创建初始状态S={Xi0，Yj0，Zk0，Wl0}。然后，通过计算index(0)得出P(0)的选定变量slt(0)。系统状态更新如下:

(5)

同理，通过计算index(1)，从P(1)的更新状态S中得到选定变量slt(1)，并更新系统状态。依次得到P(n)的更新状态变量集S，并通过计算index(n)从S中选择状态变量slt(n)。假定P(n)的状态为Xi、Yj、Zk、Wl。为了不失一般性，假定index(n)=0。这种情况下，选择状态值Xi对P(n)进行加密，状态变量组合为{Xi+1，Yj，Zk，Wl}。类似地，计算index(n+1)，并设index(n+1)=1。则状态值Yj将被选择以加密P(n+1)，而状态变量组合则变为{Xi+1，Yj+1，Zk，Wl}。同理，假定index(n+2)=2，则状态值Zk将被选择以加密P(n+2)，那么状态变量组合变为{Xi+1，Yj+1，Zk+1，Wl}。假定index(n+3)=3，则状态值Wl将被选择以加密P(n+3)。

2 本文彩色图像加密方案

2.1 密钥流生成程序

密钥流生成程序(Key stream generator programming，KSGP)用于加密程序的不同步骤，其简要过程如图1所示。即使仅有一个像素发生变化，CDSVSP也能够从选定变量中有效生成完全不同的序列。因此，KSGP可以得出随机密钥流，并支持以最少资源实现高安全标准。

图1 密钥流生成程序

本文基于通过式(2)迭代得出的相同混沌数据，生成完全不同的随机密钥流。设I=(RO，GO，BO)为给定的3个8位像素值的一维数组，大小为MN。为确保任意一个通道中单个像素值的变化会导向完全不同的密文图像，利用以下公式得到RO、GO和BO的线性组合[15]:

S=mod(αRO+βGO+γBO，256)

(6)

式中:α、β、γ是密钥的一部分，且均为整数;S是8位像素值的一维数组，大小为MN。将CDSVSP应用到S，可以得到选定状态变量slt，并用其生成密钥流K

K(i)=mod{round[abs(slt(i))-

floor[abs(slt(i))]]×1015，256}

(7)

式中:floor(x)表示x向下取整;abs(x)为x的绝对值;mod(x，y)表示x除以y的余数;round(x)为x值的舍入函数;i的数值范围为从0到MN-1。

2.2 加密过程

2.2.1 四方向扩散机制

利用不同密钥流，将KSGP应用到明文图像I上3次，以生成3个密钥流K1、K2和K3。然后，利用这些密钥流对I进行扩散，以得到I1=(RO1，GO1，BO1)，可以根据式(6)获得。

本文根据密钥流K1、K2和K3，设计了不同的扩散方法(10进制)，这些扩散方向如图2所示。第1种是从下到上扩散，第2种是从左下到右上的扩散，第3种是从左上到右下的扩散，第4种是从顶左到底右的扩散。随着加密方向的增多，获得的密文是完全不一样的，因此，图像加密的安全性明显增加。以标准Lena图像为例，其密文的熵值明显增加。第一个方向扩散的密文图像熵值为7.825 4，当两个方向扩散时，其密文的熵值为7.891 6，三个方向的密文熵值为7.940 1，四个方向的密文熵值为7.998 1。这说明在安全性方面，四个不同方向的扩散机制比某一方向扩散的表现更佳。这样，从四个不同的方向来替换RGB图像的像素值，可以明显扩散密文的随机性，并增加其抗攻击的能力。

图2 提出的四方向扩散机制

此外，将KSGP使用若干次，基于CDSVSP和所有红、绿、蓝三个通道的线性组合，生成密钥流。由此，任何一个通道中一个像素的变化，将引发CDSVSP中选定变量的不同序列，从而导出完全不同的密钥流。在所有通道上进行了像素值重新排列，因此在生成不可预测的密钥流的过程中，通道的任何位置上的像素变化都会造成相同程度的影响。总之，密钥流与明文图像的像素值直接相关。

2.2.2 置换

2.2.3 生成密文图像

按照上一节，对密钥流Ki(i=1，2，3)与I=(RO，GO，BO)进行扩散，以改变像素值，从式(6)可知两者是相互混合的。使用伪随机数序列将8位十进制像素值转换为长度4的序列。然后，将8位像素值的三个大小为MN的一维数组RO、GO和BO分别转换为大小为M×N的红色通道R′、绿色通道G′和蓝色通道B′。最后，通过红、蓝、绿色通道，生成密文图像(R′，G′，B′)作为本文图像加密方案的输出。

2.3 解密过程

解密过程通过在接收器处逆向进行加密过程，以获得明文图像。图3给出了本文解密过程的流程图。首先，CDSVSP生成四维混沌值，KSGP利用已有密钥流，合并得到解密器;然后进行去混淆操作，输入的密文图像进行去串联，密文图像进入解密器，得到解密图像。

图3 本文RGB彩色图像的解密

3 仿真和安全性分析

图像加密领域需要应对各种不同的攻击，常见的攻击包括选择明文/密文攻击，统计攻击，蛮力攻击，熵攻击等。设计加密技术时必须重点关注对这些攻击的抵御能力。在对所提方案进行性能分析时，使用了8个不同的彩色图像，尺寸均为256像素×256像素。使用USC-SIPI图像数据库中的图像“Lena”、“Baboon”、“Peppers”、“Tree”、“House”、“Beans”、“F16”和“Girl”。方法实施的平台为Intel(R)Core(TM)i7双核、8 GB内存、Windows 7操作系统，采用64位双精度MATLAB R2016编程。

为实施本文方案，四维混沌动力系统的初始值和系统参数如下:x0=17，y0=25，z0=118，w0=5，a=-10，b=3，c=-1，d=-2，b1=1，b2=-1，b3=1，b4=1。此外，在求解CDS时取足够小的步长，以避免任何不良行为和衰退效应。

3.1 密钥空间及密钥敏感性

密钥空间是图像加密的重要指标。理论上，密钥空间越大越好，即使算法稳健度很高，但如果密钥空间过小，则可能会被蛮力攻击破解[17]。本文加密方法中包含12个不同的系统状态和参数，即x0、y0、z0、w0、a、b、c、d、b1、b2、b3、b4。给定计算精度10-15，则本文加密方法的密钥空间为10212。

表1给出了本文加密方法与其他先进方法的密钥空间，其中，本文加密方法的密钥空间组成是:CDS、KSGP、十进制转换、四方向扩散。一般标准的密钥空间大小应该不低于2100，因此，本文图像加密算法的密钥空间远大于标准空间，同时比文献[6，7，8]方法的密钥空间更大。

表1 各方法的密钥空间比较

密钥敏感性是评估图像加密安全性的重要指标，如果密钥的任何极小改动都会导致巨大改变，则加密非常安全，因为只有使用完全正确的密钥才能复原原始图像。本文为了评估密钥敏感性，使用非常微小差异的密钥流对图像进行加密。初始状态x0作细小改动:x0=x0+10-15;x0=x0-10-15。使用该密钥流对相同的图像进行加密和解密，得出该参数的敏感性测试结果如图4所示。由图可知，对应的MSE都在3500以上，出现了雪崩现象，这说明所提方法的密钥敏感性非常强。

图4 密钥敏感性测试

3.2 差分攻击(明文敏感性)

攻击者会尝试各种可能方式以得到原始图像，其中一种方式是在输入明文图像中作细微更改，然后对更改前后的明文图像分别进行加密，以寻找明文图像和加密图像之间有价值的联系。

像素改变率[18](Nnumber of pixels change rate，NPCR)和统一平均变化强度[19](Uniform average change intensity，UACI)是测试明文图像中单个像素更改对加密图像的影响的两个度量。这两个指标分别定义为

(8)

式中:M和N为图像尺寸，D(a，b)可表示为

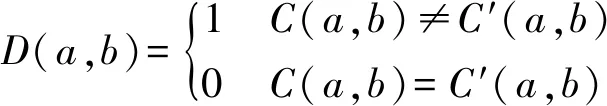
(9)

100%

(10)

式中:C和C′分别为明文图像中单个像素更改前后的密文图像。

各方法的差分攻击度量NPCR和UACI数值如表2所示。

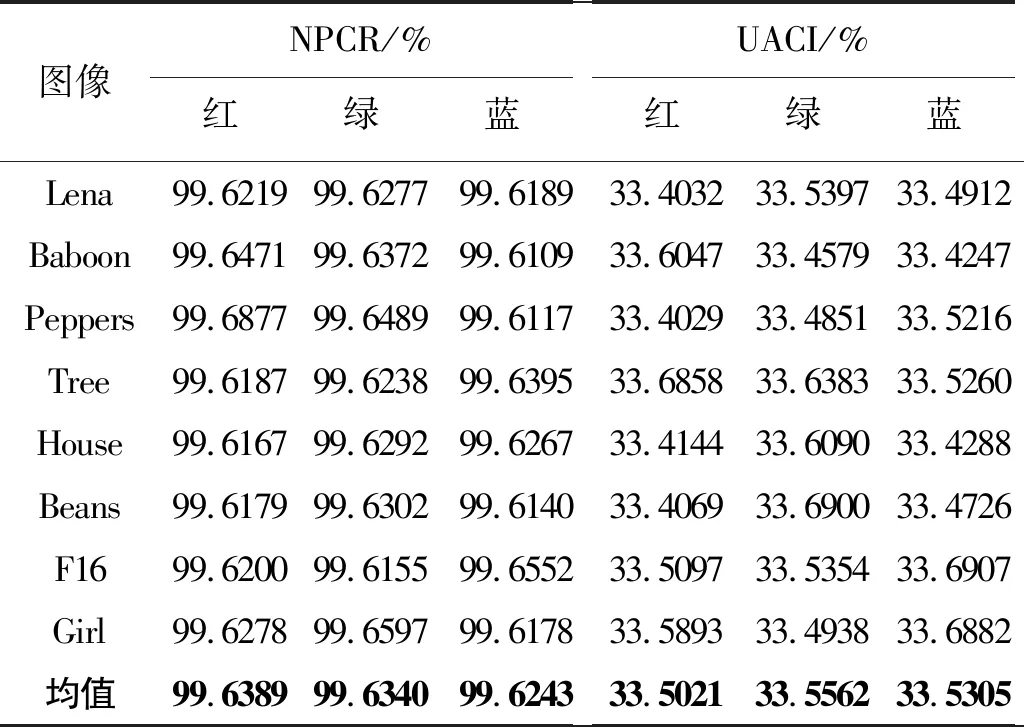
表2 本文方案不同图像的NPCR和UACI值

从表2中可观察到，NPCR和UACI的平均值分别为99.6300%和33.5296%，这证明了所提方案能够抵御差分攻击。由表3可知，对于Lena图像，本文算法在NPCR和UACI方面的性能优于文献[6，7，8]的算法。

表3 不同方案的NPCR和UACI均值法

3.3 生成密钥流的随机性

本文方法使用了较少的混沌数据，从而实现较高效率。为了分析生成的密钥流是否完全随机且彼此互不相关，本文计算了两者之间的NPCR和UACI，实验部分生成密钥流6次。如表4和表5所示，NPCR>99.6，UACI>33.4。由此证明，本文方案最大限度减少了资源使用，且并没有降低安全性。

表4 密钥流之间的NPCR

表5 密钥流之间的UACI

3.4 直方图统计分析

图像的直方图描述了像素强度分布，攻击者可利用图像的直方图获得一些有价值信息。因此，在加密过程后，密文图像的直方图应该尽可能均衡。图5和图6分别展示了Lena图像明文和密文的直方图。明文图像中，柱形并不均衡，存在较大波动，包含很多攻击可用的信息。而密文图像中，柱形非常均衡，攻击者无法从中得到有用信息。

图5 Lena明文图像直方图

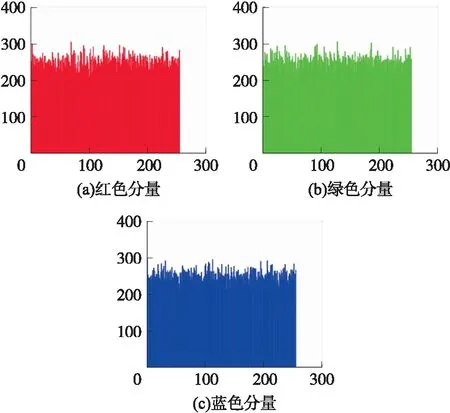
图6 Lena密文图像直方图

方差是衡量数据/信息在平均值附近平均分布的度量。低方差意味着分布中数据点之间的差异较小。所以较小方差值有利于保持直方图的均衡性。加密测试图像(Lena、Baboon、Peppers、Tree、House、Beans、F16和Girl)的直方图的方差值如表6所示，给出了Key0、Key1、Key2和Key3。利用初始密钥Key0计算出表6第一列中的方差值，剩余列的方差值则通过更改Key0中的单个密钥而得到。从表6可发现，使用本文方案时，密文图像的方差值约为800，输入明文图像的方差值约为86 488。结果表明，本文方法能够有效降低方差值，实现了较好加密效果。

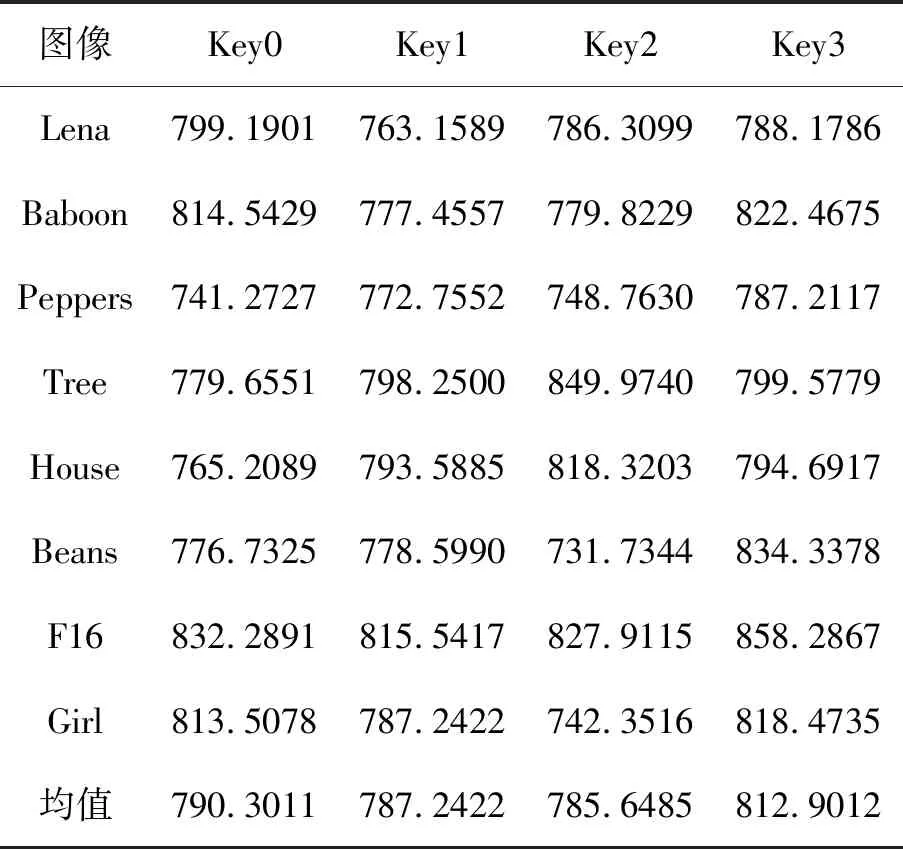
表6 不同密钥下的加密图像直方图的方差值

3.5 信息熵分析

信息熵是一个信息随机性的度量。以概率pi(i=1，…，r)取r个不同数值的随机消息U，其不确定性(熵)的定义为

(11)

在安全的密文图像标准中，其熵(H)理论上应为“8”，实践中应该接近8。熵值越接近8表示效果越佳。图7是本文方法的初始明文和加密密文。表7给出了不同密文图像的熵。从表7的结果中可发现，相比于其他方法，本文密文图像的熵接近8，因此，本文方案能够抵御熵攻击。

图7 初始明文与加密密文

表7 不同加密方案的加密图像信息熵比较

3.6 峰值信噪比分析

图像加密算法应在输入明文图像和相应密文图像之间建立最大差异。峰值信噪比(PSNR)是测量输入图像及其密文图像之间差异的度量，其定义如下

(12)

(13)

式中:M表示图像宽度，N表示图像高度。P0(i，j)和P1(i，j)分别为原始图像和加密图像的像素强度值。MSE为原始图像和加密图像之间的均方误差。较大的MSE值将生成较小的PSNR值，从而提供更好的加密安全性。

本文加密方法与其他加密方法的PSNR值如表8所示。其中，“O”、“C”、“D”分别表示原始、加密和解密图像。使用本文算法时，明文图像和解密图像之间的PSNR值为(∞)。这说明明文输入图像和解密图像之间没有差异(MSE=0)，即加密和解密算法没有丢失任何像素强度值。因此，所提方案的PSNR值低于其他方案[6，7，8]，具有更好的安全性。

表8 明文图像与解密图像间的PSNR结果比较

3.7 时间复杂度分析

在安全性之外，图像加密算法应具有较快的运行速度以满足实际应用需求。为了分析时间复杂度，本文考虑了混沌数据生成和加密算法两个方面。通过将CDSVSP应用到数组S，生成混沌数据K。其复杂度为O(4MN)，其中(M，N)为给定输入图像大小。四个方向扩散操作的复杂度为O(6MN)。置换和进制转换的复杂度为O(2MN)。因此，本文方案的总复杂度为O(12MN)，优于文献[6]的O(24MN)和文献[7]的O(64N2)，以及文献[8]的O(128N2)。

4 结束语

所提方案通过CDS得出的混沌数据质量很高，且CDSVSP能够以极高效率从中生成完全随机选择的序列。同时，明文图像的像素直接参与到所有加密步骤。此外，所提方案为每个像素使用不同的转换规则，并采用了四个不同的扩散方向机制，增加了密文图像的随机性，从而实现更好的加密性能。仿真和实验测试结果表明，所提加密方案能够保持高标准安全性，且使用的资源比其他加密方案小得多，具有低时间复杂度、高效率和高安全性，对图像安全领域具有借鉴意义。本文方法的一个局限是对较大尺寸的彩色图像加密时，会使得像素的10进制转换计算和多方向扩散的计算量明显增加，如果优化大尺寸图像的加密将是本文未来研究重点。