不确定规划中循环可达状态信息的维护*

张潇妮 文中华，2 彭擎宇

（1.湘潭大学信息工程学院 湘潭 411105）（2.湖南工程学院计算机与通信学院 湘潭 411104）

1 引言

智能规划的基础模型通过图来建立［1］，近年来，对智能规划的建模从确定图模型扩展到不确定图模型［2］。不确定规划放宽以往经典规划的一些基本假设，使之更接近实际情况的解答，现已应用到不少领域中。

在不确定规划［3］中，有许多求解不确定规划解［4～6］与一些复杂查询的问题研究（如：蛋白质分子之间是否有交互作用，找寻网络安全中的不确定攻击图的攻击路径［7～8］等）。在求解与查询过程中，由于状态之间的可达信息缺乏，会有大量重复的搜索，因此，有不少学者在可达性查询［9］研究取得重要成果，如：基于树形结构的可达性查询［10～12］，利用矩阵的性质求解状态之间的可达性［13～15］等，基于区间树的求解算法只能尽大可能地获取节点之间的可达关系，不能良好地求解整个系统中的各个节点之间的可达关系。在动态环境中，对状态可达性的研究更多的是基于状态之间的确定可达的操作，若是可达即为确定可达，否则为不可达，忽略了状态之间的不确定可达，此外，对有向图的要求大多是无环的。

在不确定规划中，它考虑了每一个动作效果的存在性，也就考虑了状态之间的可达性的不确定性。本文通过矩阵来建立问题模型，充分考虑状态之间的动作执行的不确定性，准确表达状态间的可达性（确定可达、不确定可达与不可达），提出了一种新的状态可达关系的维护算法，对动态环境下的不确定性动作的存在变动性所影响的状态之间的可达关系进行局部更新维护，适用于循环不确定系统中。该方法根据已有的信息可达矩阵和变更之后的不确定系统的邻接矩阵的信息，重新进行转发，对可达矩阵进行局部更新，取得新的状态可达矩阵，避免重新求解。

2 相关定义

定义1：一个三元组可表示为规划领域中的不确定的状态转换系统，即∑=＜S,A,γ＞其中：S是一个有限状态集；A是一个有限动作集；γ:S×A→2s是状态转移函数。

定义2：设∑=＜S,A,γ＞是一个不确定状态转移系统，从状态si开始，执行γ=(si,ax)之后，可能到达的状态集合SL={s|s∈(sx,ax),s∉{s1,s2,…,sn},1 ≤x≤n} 中的一个状态，若si∈γ(sj,aj)(∃i,i＜j)，则称∑=＜S,A,γ＞为循环不确定状态转移系统s∈γ(sj,aj)(∃i,i＜j)，否则为非循环不确定状态转移系统。

定义3：在一个不确定状态转移系统中，用函数d(s1,s2) 来表示s1和s2两个状态间的可达关系。可达关系定义如下：

当状态s1存在一条非循环路径确定可达状态s2时，则称s1到s2确定可达，d(s1,s2)=1；

当状态s1存在一条路径L并且s2∈SL时，则称s1到s2不确定可达，d(s1,s2)=T；

当状态s1的任意一条路径L都有s2∉SL时，则称s1到s2不可达，d(s1,s2)=0；

其中状态自己到状态自己为确定可达d(si,si)=1(1 ≤i≤n)，此类关系构成的矩阵即是可达矩阵。

定义4：通过一个唯一标识关联区分不确定状态转移系统中任意不确定动作，记为Tx。状态si执行Tx后可能到达的状态集合Tx.mark={sm,sn,s0,…,sz}称为不确定动作Tx的信念状态。Tx.num是不确定动作Tx的信念状态个数。

定义5：在一个不确定状态转移系统，用s-i→s-j表示将状态si的可达信息s-i传递给状态sj，d'(si,sj)表示经信息传递后获取的状态si到状态sj的可达关系。其信息传递原则如下：

若d(si,sk)=1，d(si,sj)=1||T||0 ，则s-i→s-j：d'(si,sj)=1；

若d(si,sk)=0 ，d(si,sj)=1||T||0 ，则s-i→s-j：d'(si,sj)=d(si,sj)；

若d(si,sk)=Tn，d(si,sj)=Tm，则s-i→s-j：d'(si,sj)=Tn+Tm；

若d(si,sk)=Tn，d(si,sj)=Tn，si-j[Tn].value=si-j[Tn].value+card(si-k[Tn].mark-(si-j[Tn].mark∩sk-j[Tn].mark))，当si-j[Tn].value=Tn.value，则s-i→s-j：d'(si,sj)=1，否则为d′(si,sj)=Tn。

3 算法思想

3.1 状态标记

状态标记记录着该状态的最新状态信息的更新是经哪个状态传递的，更新原则如下。

1）不确定系统的邻接矩阵中所有状态的初始标签tag均为0，若经由传递后可达信息不变，tag 仍记为0。

2）状态间的可达关系经传递后形成确定可达关系或是由不可达成为不确定可达时，则更新为最新传递可达信息的状态；

3）判断可达关系是否不确定时，若根据原状态si与sv的可达关系，状态sv与状态sx的可达关系，可得知状态si到状态sx的可达关系，此时记录six.tag为最后一状态编号加1。

当系统中状态si与sv的执行动作因其它因素发生变动（包括边的添加与删除操作），则需重新判断状态si与状态sv的可达关系，与原系统的可达矩阵中的对应信息对比，若是不一致，则说明该状态的可达信息变更了，因此经该状态sv作为中间状态传递的可达信息也就会受到影响，需进行更新；否则，无需更新。在此过程中，也会有状态不受该执行动作变动的影响，但仍需对其进行转发，直至受其影响的状态均进行比较、转发操作或可达信息不再变更时，则该系统的状态确定可达信息已求解出。

3.2 状态可达关系更新

状态之间可达关系更新步骤如下。

1）若状态si与sv(i＜v)的可达关系变动，则将可达矩阵R中满足s-v.tag＞=i的状态sv的可达信息恢复到变更后的邻接矩阵B的状态sv对应可达信息，同时将状态si（s-v.tag＜v）的可达信息再次传递到状态sv。

2）若可达信息里原状态可达矩阵D的状态sv与当前状态sv不一致，则将sv中s-v.tag＜v的信息重新进行传递，将需要更新的状态（sx.tag＜v）的可达信息（需满足s-x.tag＞=v）恢复为变更后的邻接矩阵B的该状态对应的可达信息，再进行传递，更新记录可达信息变更的最后一状态Colcmax，与其状态可达标记。

3）状态sv的可达信息传递之后，再将下一状态sv+1且sv+1.tag＜v+1的可达信息进行传递，判断哪些状态的可达信息需要进行更新，重复2）操作。

4）依次进行转发，直到最后更新的状态的可达信息与原可达矩阵一致或者最后一个状态的信息进行转发，则结束与原状态可达矩阵的比较。

5）最后，再对可达矩阵进行遍历，找出所有元素值为0的点即为不确定可达矩阵。

证明：

可达状态相关可达信息恢复到变更后的邻接矩阵对应信息，经信息的传递，不会因为缺失其它状态传递的信息而影响其最终的确定可达信息。因此，在信息传递之后，只需对找出所有不确定可达状态对即可。

1）若状态si与状态sv之间是一型确定可达，可直接通过邻接矩阵或经信息传递可得。

2）若状态si与状态sv之间是二型确定可达，有此两种情形：当si-j[Tx].value=Tx.num，且状态sv并非Tx的信念状态时，根据中间状态的可达信息，向确定可达状态的传递信息原则，则必存在状态sj(i≤j≤Colcmax) ，使得si-j[Tx].value=Tx.num，且si-j.tag＜=i，此si-j可达信息不会恢复变更后的邻接矩阵对应可达信息；当sij的可达信息由原可达矩阵的确定可达恢复到不确定可达时，即状态sv是Tx的信念状态时，根据状态向其确定可达的状态进行传递信息原则，则必存在状态sj(i≤j≤Colcmax)，且si-j.tag＜=i，si-j[Tx].value=Tx.num-1，sv=si-v[Tx].mark-si-j[Tx].mark，经信息的发送，使得si-v[Tx].value=Tx.num。

4 算法实现

设∑=(S,A,γ)为不确定状态转移系统，S为状态集合，D为∑=(S,A,γ)的原状态可达矩阵，B表示∑′=(S,A,γ′)状态之间可达关系发生变更后的邻接矩阵，R是∑′=(S,A,γ′)状态可达信息更新后的状态可达矩阵。算法如下：

根据原系统中的可达矩阵信息进行更新，第2行是对状态之间的执行动作发生变更的不确定系统∑'的邻接矩阵的更新；第3～5 行是对受其影响的状态所拥有的可达信息与原系统中的可达矩阵进行对比并根据原则更新可达信息，否则直接进行下一状态的传递，且当j=Colcmax时，结束更新；第6 行FINDCERTAIN（∑，R）函数是根据确定可达的状态标签快速找出变动后不确定系统∑',γ')其影响的状态，并需将其状态可达信息进行传递，取得受其影响的其它状态对之间的可达信息；第7 行是对不确定系统∑',γ')中状态之间的不确定可达关系进行修正。

函数FINDCERTAIN（∑，R）的具体实现过程如下：

第4行收集状态si所拥有的可达信息。第5～7行寻找状态si确定到达的状态并将其可达信息传递给状态sk，第8 行更新状态变更的最大编号，确保受其影响的状态都进行了判断。其中函数DELIVER（sk，s-i）的实现过程如下：

5 算法实例及仿真实验分析

如图1，设∑=(S,A,γ) 为不确定状态转移系统。将通过文中描述的信息传递优化算法对此转移系统进行维护。

图1 原不确定状态转移系统

参考文献［15］的算法可得该不确定系统的状态可达矩阵如下：

若因为一些原因使其不确定系统的状态s1与s2由确定可达变成不确定可达T3，与其它不确定动作进行区分，此时的不确定状态转移系统如图2所示。

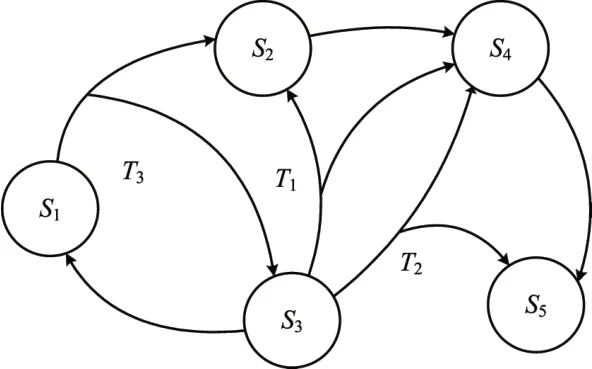
图2 可达关系改变后的不确定系统

其邻接矩阵变更为

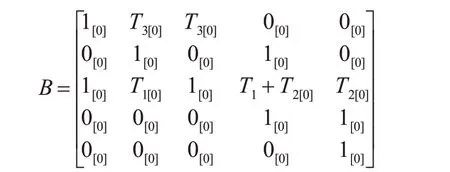
因状态s1到状态s2与s3的可达信息都发生了变动，所以需将原可达矩阵D中可达状态s2与s3中分别满足s-2.tag＞=1 与s-3.tag＞=1 的可达信息恢复到变更后的邻接矩阵B的状态s2与s3的对应可达信息，此时Colcmax=3，可得：

重新将状态s1的可达信息进行信息传递，根据R[1][j].tag＜1 且R[1][j]=1 的条件，可知状态s1无法进行转发。

但R[i][2]≠D[i][2]且Colcmax=3，则状态s2需重新进行信息传递，根据R[2][j]=1 且R[2][j].tag＜2 条件，可知R[2][3]=1，将可达矩阵R中状态s2的可达信息传递给状态s4，先将可达状态s4的满足S-4.tag＞=2 的可达信息恢复到变更后的邻接矩阵B的状态s4的对应可达信息，再将R[i][2].tag＜2 的状态可达信息进行转发，根据传递规则，得：

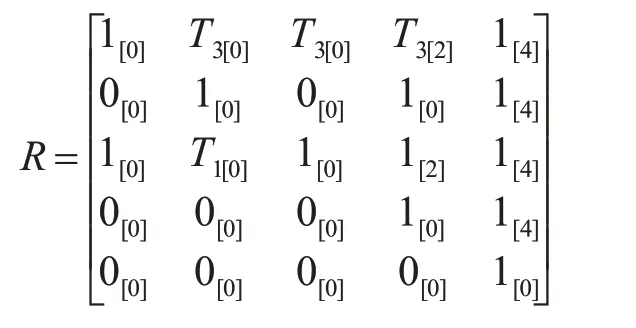
R[2][j]=1 再由状态s3进行信息传递，根据R[3][j]=1 且R[i][3].tag＜3 条件，可知R[3][1]=1 和R[3][4]=1，因此可达矩阵R中状态s3将自己的可达信息传递给确定可达的状态s1和状态s4，此时Colcmax=4 根据信息传递规则可得：

R[i][4]的可达信息D[i][4]的可达信息相等，且Colcmax=4，因此不需再更新。

这样已找出了变更后的不确定系统中所有确定可达关系，最后对更新后的可达矩阵R中元素值为0 的状态可达关系进行判断，最终得到的可达矩阵为

仿真实验对比如下。

以下为采用本文改进的信息传递方法维护状态可达关系与采用信息传递法、矩阵相乘法重新进行更新系统的状态可达关系的实验结果比较，三个算法的输入数据均相同，运算时间如表1所示。

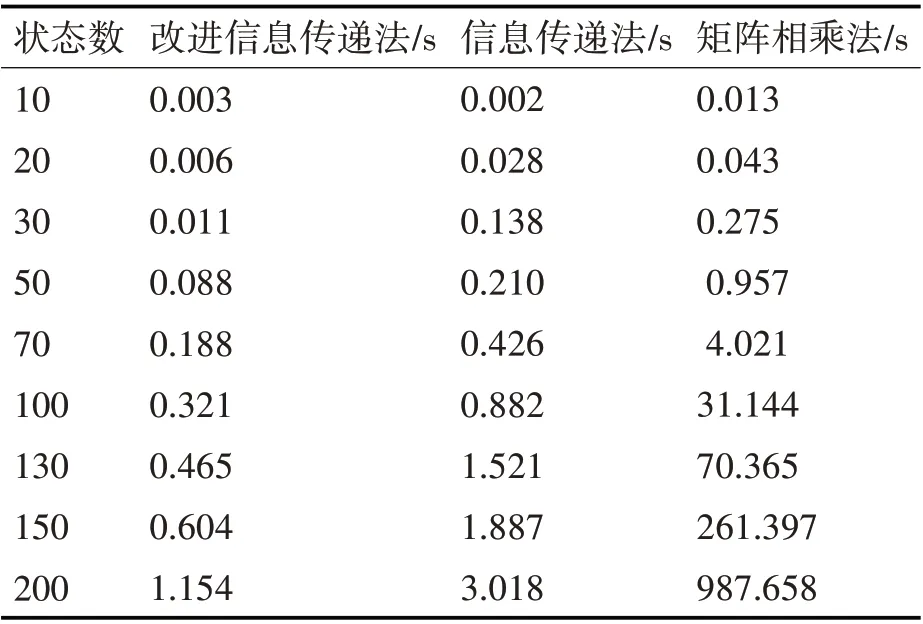
表1 运行时间对比

当状态数较少时，系统中的动作也会比较少，状态之间的可达路径会屈指可数。当系统中的单个动作执行发生变动时，可能会牵引到整个系统的状态之间的可达关系的变动。因此，此时系统中可达关系的局部维护与重新求解系统中可达关系的运行的时间相差不大。

当系统中状态数逐渐增加时，其系统之中的动作也随之增加。由于状态之间的可达关系可以通过其它动作的执行与其它状态间接取得联系，从而一个执行动作的变动一般也不会影响整个系统中的状态可达关系。因此，该动作的变动影响的大多数是系统中的局部状态之间的可达关系，从而它的求解运算量会比重新求解系统中的可达关系小很多，从而提高效率，且比文献［15］所运行的时间要少。

6 结语

本文从不确定系统中的信息传递方法切入，为加强算法的适用性，深入挖掘各个状态维度的可达信息，快速求解系统的可达关系，维护不确定系统的相对稳定性。今后的进一步工作有：

1）完善系统传递方法，进一步提高求解效率。

2）将传递法的思想应用到多Agent 系统，或求解不确定规划的规划解中。