基于加权K-means聚类算法的机动通信网络自动划分方法

王均春 冀云刚

摘要：针对机动通信网络规划中的网络划分需求，提出了一种基于加权K-means聚类算法的网络自动划分方法。算法通过采用Elbow方法确定聚类数量，并在初始聚类中心选择中考虑了节点连通度，克服了传统K-means算法初始聚类中心的不确定性，通过对不同特征分配相应权重，进一步提升了聚类效果。实验结果说明该算法在机动通信网络自动划分中具有良好的准确率，为后续网络规划提供了基础支撑。

关键词：网络划分;加权K-means;网络规划;节点联通度

中图分类号：TP393文献标志码：A文章编号：1008-1739（2022）02-56-4

0引言

机动通信网络是为保障特殊任务而临时开设的综合性通信网络，具有快速开设、组织结构复杂、动态变化等特点。机动通信网络规划负责在网络开设前，根据通信保障需求统筹安排各类通信资源，进行网络拓扑规划、频率规划、IP规划等，生成网络开通所需的规划参数文件，确保网络快速开通。其中，网络拓扑规划是基础。在开展其他规划工作前，需先根据网络拓扑结构和网络组成，将整个网络划分成若干相对独立的子网，然后再基于子网划分结果进行各子网的频率分配、IP地址规划、路由协议规划、聚合路由规划等。目前在进行子网划分时，一般多采用人工划分或按所属单位固定划分方式，缺少自动化手段，无法适应机动通信网络组织结构灵活多变的特点。尤其是当网络规模较大时，对规划人员要求高，影响网络规划效率。

K-means算法[1]作为一种经典的聚类算法，能够将样本中的对象划分成不同的类簇，从而使同一类簇中对象具备相似性，不同类簇间对象具有差异性。K-means算法由于简单、高效、良好的局部搜索能力、数据集类型多样等特点在多种学科领域广泛使用，尤其是对球状分布的数据进行聚类时能达到理想的效果[2]。但同时存在需事先确定聚类数，且对初始聚类中心敏感，初始聚類中心的随机选取导致聚类结果不稳定，容易陷入局部最优解，并易受孤立点的影响等缺点。本文主要针对机动通信网络子网划分任务，提出一种根据通信节点连通度和物理位置确定K值和初始聚类中心的方法，并设计一种加权K-means聚类算法，能够提升机动通信网络划分效果。

1相关背景

1.1 K-means算法

K-means算法属于聚类算法，是一种无监督的机器学习方法，与有监督的机器学习方法不同，K-means算法不需要具有数据的先验知识，根据数据对象的相似度对集合中数据对象进行划分[3]。从理论上说，聚类算法是将数据集中的样本划分为若干个通常不相交的子集，每个子集称为一个簇。聚类分析的最终目标是使属于同一簇的数据对象具有最大的相似度，属于不同簇的数据对象具有最大的差异度。

1.2网络结构

从网络组成方面来看，机动通信网络一般由骨干网络和用户网络组成，如图1所示，用户网络之间通过骨干网络实现互连互通。从网络规模方面，机动通信网络规模灵活可变，根据任务保障需求从几十个通信节点到几千个通信节点不等。在网络传输手段方面，根据部署位置和使用需求不同，采用光纤、有线远传、微波、卫通、自组网等多种通信手段。其中，光纤、有线远传、自组网等传输手段一般多用于用户网络，卫通、微波等多用于骨干网络。

根据机动通信网络组织结构，在进行网络划分时一般要考虑通信手段、地理位置、所属网络、业务关系等因素。

（1）通信节点类型根据在网络中位置、功能定位等不同，可将通信节点分为骨干网节点和用户网节点两类。骨干节点主要用于搭建连通各用户网的骨干网络，因此其通信手段主要满足大带宽、远距离传输需求，如卫通、微波等。用户网节点用于在小地域范围内构建用户网络，主要采用光纤、有线远传、自组网等。通信节点类型在很大程度上决定该节点在网络中的位置。因此，通信节点类型是判断该节点所属网络类型的关键因素。

（2）地理位置

通信节点间距离或覆盖地域也是反映网络特点的重要因素。一般来说，骨干网各通信节点间距离较远，多采用大跨距远距离传输的卫通、微波等;用户网通信节点间距离相对较近，一般采用有线、自组网等传输距离相对较近的通信手段。在地理位置上，一般同一网络内的通信节点位置相对集中。比如各用户子网一般限定在数公里范围之内，骨干网覆盖地域相对较远。

（3）网络连通度

从节点间互连关系来看，属于同一网络内的节点间互连关系更为紧密。比如在用户网络内一般构建全连通的自组网，在骨干网络中构建全连通的卫星网络等。因此，网络内部相比网络之间的连通度高。

2改进的K-means算法

2.1自动确定K值

Elbow法核心思想[5]是：随着聚类数的不断增大，样本划分结果也将更加精细，所划分的每个簇的聚合程度会逐步提高，使逐渐变小。在计算过程中，当的取值小于实际的聚类数目时，随着取值的不断增大，每个簇的聚合程度将大幅度提高，计算结果也会大幅下降;当值等于实际的聚类数目时，随着取值的增加，计算所得的聚合程度会大幅变小，计算结果的下降幅度也会锐减，最终会随着取值的不断增大趋于平缓。从图形上来看，和值的关系图呈现为一个手肘的形状，图中肘部对应的的取值就是数据的实际聚类数目。

2.2初始聚类中心选择

在选择初始聚类中心时，采用K-means+聚类算法中初始聚类中心的选择方法，并结合机动通信网络特点，将网络中各节点的连通度作为选择初始聚类中心的关键因素之一。初始聚类中心选择步骤如下：

①采用随机选取方式从数据集中选取一个样本点作为初始聚类中心;

在本文中，机动通信网络数据的主要特征包括节点位置、节点类型、节点连通度、节点对外连接关系等。其中，节点位置信息一般采用经纬度表示，在本文中为方便计算，采用对应的屏幕坐标。节点类型包括骨干节点、接入节点和用户节点3类。节点连通度是该节点对外的链路数量。以上3类特征分别赋予不同权值直接参与欧氏距离计算。节点对外连接关系不直接参与计算，作为独立判断因子，在进行聚类时，根据节点对外连接关系判断孤立点的所属聚类。

3实验及结果分析

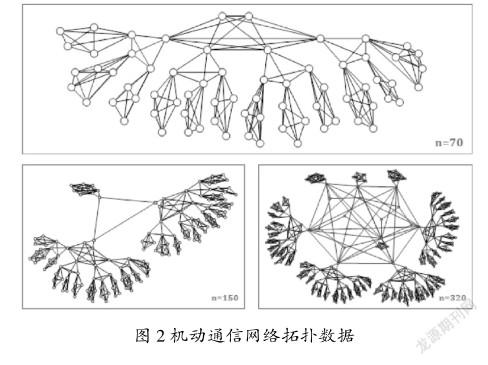
为验证本文中改进后K-means算法的实际聚类效果，分别选取了70，150，320个节点的3个不同规模的机动通信网络拓扑数据进行了测试，机动通信网络拓扑数据如图2所示。

（1）选取值

针对3个不同规模的网络拓扑数据，采用Elbow方法进行K值的选取。值与之间关系如图3～图5所示。

从图3可以看出，针对节点数为70的机动通信网络拓扑数据，当值从5开始继续增大时，SSE取值变化趋向平缓，因此选择=5作为聚类数。

从图4可以看出，针对节点数为150的机动通信网络拓扑数据，当值从3开始继续增大时，取值变化趋向平缓，因此选择=3作为聚类数。

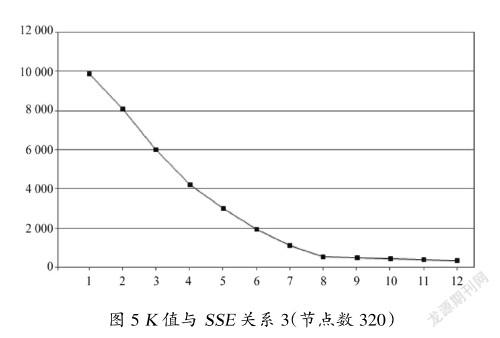
从图5可以看出，针对节点数为320的机动通信网络拓扑数据，当值从8开始继续增大时，取值变化趋向平缓，因此选择=8作为聚类数。

（2）聚类结果

3种不同规模机动通信网络拓扑数据聚类结果如图6所示。其中，在考虑节点连通度的因素下，初始聚类中心选择符合预期。

4结束语

本文针对机动通信网络规划实际需求，通过采用基于加权的K-means聚类算法，实现机动通信网络自动划分，为后续的频率规划、IP规划、路由规划等奠定了基础。通过3种不同规模网络拓扑数据的实验验证，采用的基于加权的K-means算法基本能够按照預期实现网络自动划分。

参考文献

[1]杨志，罗可.一种改进的基于粒子群的聚类算法[J].计算机应用研究，2014，31（9）：2597-2599，2605.

[2]李梅莲.基于密度分布的K-Means初始聚类中心选择算法[J].许昌学院学报，2017，36（2）：20-24.

[3] EVERITT B， HOTHORN T. Cluster Analysis[J].Quality & Quantity，2011，14（1）：75-100.

[4]黄伟明，杨建宇，陈彦清，等.基于扇形筛选法的矢量数据压缩方法[J].武汉大学学报（信息科学版），2016，41（4）：487-491.

[5] HRUSCHKA E R， CAMPELLO A， FREITAS.A. A Survey of Evolutionary Algorithms for Clustering [J].IEEE Transactions on Systems， Man and Cybernetics-Part C，2009（39）：133-155.

[6]周志华.机器学习[M].北京：清华大学出版社，2016.

[7]郭靖.对K-means聚类算法欧氏距离加权系数的研究[J].网络安全技术与应用，2016（10）：74-75

3805501908279