“等腰三角形的轴对称性(3)”教学设计
陆丽萍


“双减”背景下如何发展初中生数学高阶思维,提升课堂教学质量,达到减负、提质、增效的目的呢?本文以苏科版数学八年级上册“等腰三角形的轴对称性(3)”的教学设计为例,与大家分享交流。
一、具体分析
1.教材内容分析。
本节课是苏科版数学八年级上册“等腰三角形的轴对称性”第三课时的内容。学生在掌握了平行线性质、命题、全等三角形的性质和判定以及等腰三角形的性质等基础上,进一步探索和研究等腰三角形的判定定理和性质定理。等腰三角形的判定定理揭示了同一个三角形的边角关系,与等腰三角形的性质定理互为逆定理。等腰三角形的判定为我们提供了证明两条线段相等的新方法。因此,本节课内容起着承上启下的作用。
2.学情分析。
学生在学习了全等三角形的证明、轴对称及等腰三角形的性质后,对等腰三角形有了一定的认识,会利用全等三角形来证明边、角相等。虽然学生已经有了一定的观察、操作以及归纳推理的能力,但自主探究与合作学习仍需要进一步加强和引导。
3.学习目标分析。
探索并掌握等腰三角形的判定定理,发展合情推理和演绎推理的能力,综合运用等腰三角形的性质定理和判定定理解决问题。
二、整体建构
教师创设情境,推进单元整体教学,让学生完成自我建构或共同建构,在课堂学习中优先达到高阶思维目标。
师:在上课前,同学们先回顾有关轴对称的知识,和之前学的知识作类比,并与全班同学讨论,我们将学习哪些新知识?
生1做了一个本章知识的知识脉络图并展示。
生2:前面我们学习了线段、角的轴对称性,知道了图形的定义,研究了性质及判定方法。上节课我们学习了等腰三角形的性质,接下来,我们还要研究等腰三角形的判定方法。
学生活动:学生自主回顾之前学习的命题相关知识以及等腰三角形的性质,整体建构,用类比学习的方法独立思考并解决问题。
师:对于“等腰三角形的两个底角度数相等”这个命题而言,它的逆命题是什么?
生3:有两个角相等的三角形是等腰三角形。
师:这个逆命题是真命题还是假命题?
生4:真命题。
学生活动:先独立思考,提出猜想,再在组内发表自己的看法。
设计意图:引导学生逆向思考,体会构造逆命题也是探索、研究和认识图形的重要途径。
三、以“问”为先
活动1:问题教学,合作探究。
数学高阶思维能力一般包括:问题解决、推理、表达、构思等。而问题解决能力是高阶思维的核心能力。以“问”为先的学程重构就是教学中以问题为主线,贯穿课堂的始终,激活课堂,让学生在自主、独立地寻求并运用已有的知识经验完成探索数学知识的过程中,发展数学抽象、推理、模型的思想,促进高阶思维的发展。
例1 在一张长方形的纸条上任意画出一条截线AB(如图1),所得的∠1与∠2相等吗?为什么?沿AB折叠后,得到△ABC(如图2),其中∠1=∠2,度量边AC、BC的长度,你有什么发现?你能证明吗?
学生活动:学生通过实践操作、小组交流,进行总结。笔者随机选取了2个小组进行展示。
设计意图:让学生动手折叠测量,从感性上感受等角对等边,为下一环节的证明做铺垫。
笔者结合学生的发现,提出问题:你能证明你的发现吗?
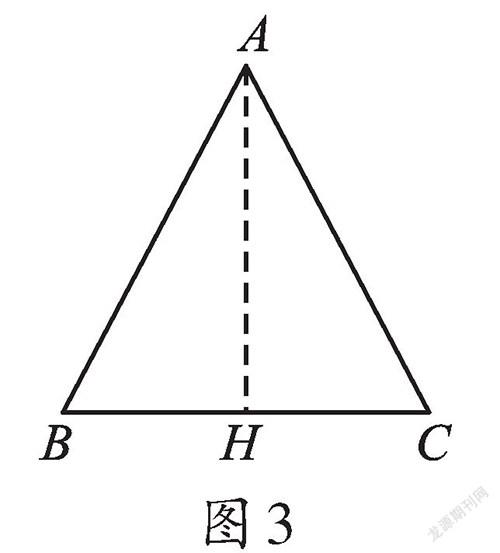
例2 已知:如图3,在△ABC中,∠B=∠C。求证:AB=AC。
学生活动:小组讨论并发表看法,归纳总结出不同的证明方法。
设计意图:学生由前面“等边对等角”的证明得到启发,通过添加辅助线,构造两个三角形全等,来证明上述结论;通过生生互动、师生互动,归纳总结作辅助线证明等腰三角形的判定定理的方法。
活动2:知识巩固。
例3 已知:如图4,在△ABC中 ,∠ABC=72°,∠C=72°。
(1)图中相等的线段有 ;
(2)若BD平分∠ABC,则∠1= ,∠2= ;
(3)图中等腰三角形有 个。
学生活动:学生独立完成;学生之间互评。
设计意图:直接利用“等角对等边”解决问题。
例4 已知:如图5,在△ABC中,BD平分∠ABC,DE//BC,求证:BE=DE。
例5 已知:如图6,在△ABC 中,OB平分∠ABC,OC平分∠ACB,过点O作BC的平行线交AB、AC于点D、E,
(1)证明:DE=BD+CE;
(2)若AB=18,AC=12,求△ADE的周长。
学生活动:先独立思考,尝试解决问题;再小组讨论,交流分享自己的思路;最后,小组代表上讲台交流分享。
四、以“学”为本
学生在学习的过程中,通过“独学”“对学”和“群学”等学习方式,实现自我建构和共同建构,进而形成高阶思维。可以说,“学程”实践研究是为了让学生像学科专家一样思考,不仅实现自我建构,还要促进共同建构,指向高阶思维发展。
师:结合角平分线、平行线、等腰三角形的知识,你能提出什么问题?
设计意图:在此环节中,学生对于有关等腰三角形的一个很常用的基本图形有了一定的认识。这个基本图形中的“角平分线、平行线、等腰三角形”,三者中满足任意两个条件,则剩下的条件也成立。熟练运用这个结论,对解决含有这个基本图形的较复杂的题目很有帮助。
生5:如图7,在△ABC中,BO平分∠ABC,CO平分∠ACF,過点O作BC的平行线交AB、AC于点D、E,则线段DE、BD、CE有什么关系?说明理由。
学生活动:学生根据题意提出问题,分析问题,在小组内进行讨论,交流解题思路,最后,派小组代表上讲台分享解题过程。
设计意图:面向全体学生,同时注重个体差异,加强练习的针对性。全体学生积极参与小组交流,提出自己的看法与意见,激发解题兴趣。
五、以“思”为要
伴随着教育改革的大力推进,初中数学教学重点正在发生根本性变化。在课堂教学中,教师应引导学生进行思维训练,让学生深度思考,变式训练,达到举一反三的效果,努力培养学生分析、综合、评价等数学高阶思维能力,从而提升课堂教学的质量和效果。
六、教学反思
对学生而言,实际应用是个难点。教师在利用等腰三角形的性质解决问题的教学中,应注意以下几点:
1.在教学设计中要体现以下目的——训练学生的建模能力,提高学生提出问题、分析问题和解决问题的能力。
2.在教学中要根据学生实际水平,对于难度较大、综合性较强的问题,要通过分步引导,将复杂问题分解为若干个简单问题,步步深入,由易到难地寻求答案。
能使学生自主学习、主动发展的课堂才是好课堂。自主学习是最重要的学习方法和手段。教师在课堂上的主要任务是引导学生独立思考,自主探究,让学生自己去发现问题、分析问题、提出问题、解决问题,这样,学生的自主学习意识就会逐步增强,自主学习能力就会大幅提高,高阶思维的发展有了保障,在一定程度上提升课堂教学质量,达到减负、提质、增效的效果。

