基于平滑变结构-卡尔曼滤波的目标定位方法
许剑锟,金国栋,谭力宁,许剑锋,薛远亮
(火箭军工程大学,西安 710000)
0 引言
无人机高精度目标定位在军事侦察、精准打击、抢险救灾等方面具有迫切的应用需求[1-2]。目前常用的目标定位方法是基于空间几何关系,利用无人机姿态、位置信息,以及光电平台获取的无人机与目标相对位置关系,通过齐次坐标转换进行目标位置解算[3-4]。受设备制造水平、应用环境等影响,该方法引入了大量测量误差,需要使用优化或滤波的方法来抑制噪声影响,提高目标定位精度[2-4]。卡尔曼滤波(KF)及其衍生算法是便于计算机实现的递推最优估计方法[5]。穆绍硕等[6]提出了一种基于扩展卡尔曼滤波(EKF)的算法进行迭代优化,比采用地球椭球模型的算法精度有了明显提高;郑艺等[7]提出滑动后向递推的EKF算法,与传统滤波向前递推结合,增加数据的反复利用,降低滤波误差;徐诚等[8]采用无迹卡尔曼滤波(UKF)处理视轴角和目标位置之间的非线性关系,减少了因泰勒展开截断造成的误差;唐大全等[9]提出了一种由极大似然估计法确定迭代条件的自适应迭代无迹卡尔曼滤波(Adaptive Iterative Unscented Kalman Filter,AIUKF)算法,提高了滤波收敛效率。以上方法对传统卡尔曼滤波算法都做出了一定改进,提高了滤波性能,但都是在高斯噪声模型的前提下,在非高斯噪声情况下,滤波估计误差会增大,甚至会滤波发散。
平滑变结构滤波(Smooth Variable Structure Filter,SVSF)是一种次优估计算法,它运用变结构和滑模控制概念,将估计值限制在存在子空间内,使得预估值逐步逼近真实值,对系统受到大扰动、噪声不符合高斯分布等情况具有较好鲁棒性[10-11]。
为了克服卡尔曼滤波对噪声高斯特性的限制,本文设计了平滑变结构和卡尔曼组合滤波算法,有效提高了大扰动、噪声不确定情况下目标定位的精度和算法鲁棒性。
1 测向交叉定位原理及数学模型
微小型无人机在对目标定位过程中,一般采用测向交叉的目标定位方法,即无人机在多点对目标进行观测,观测直线交点为目标位置点,如图1所示。

图1 测向交叉目标定位Fig.1 Target location by direction cross
无人机在发现目标后,通过跟踪算法和伺服系统,可以将目标锁定在摄像机视场中心,再利用摄像机的方位角、高低角和无人机的姿态角、位置坐标等数据,机载计算机或地面站即可解算出目标的位置。
1.1 视轴方位角计算
合理的辅助坐标系能够方便计算。定义辅助坐标系如下:无人机站心坐标系,又称地理坐标系,简记为N系,坐标原点为全球定位系统(GPS)接收机中心,采用北东地表达方式;载机惯性坐标系,简记为I系,坐标原点为惯性测量单元(IMU)中心,载机航向角φ、俯仰角θ、横滚角γ,代表该坐标系相对站心坐标系的3个姿态角;摄像机坐标系,简记为C系,坐标原点为摄像机光心,Z轴与摄像机光轴重合,指向目标,光轴指向角以方位角η和高低角ϑ表示。
以站心坐标为基准定义视轴角(α,β),α为视轴矢量与站心坐标系Z轴夹角,称为视轴高低角;β为视轴矢量在水平面投影与X轴的夹角,称为视轴方向角。
假定目标被锁定在视场中心,则其在C系坐标可表示为tC=(00f),其中,f为摄像机焦距。根据坐标齐次转换理论,目标在站心坐标系下的坐标可表示为
(1)
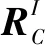
根据式(1)和图2,视轴角可表示为

图2 视轴角计算示意图Fig.2 The calculation of LOS angle
(2)
1.2 滤波方程建立
无人机发现目标后,在目标上空进行盘旋飞行,进行多次拍摄测量。假设无人机对目标共进行K次测量,第k次测量时,无人机的位置为(xUAV,yUAV,zUAV),目标位置为(xT,yT,zT)。采用状态空间模型法构建状态方程,选取离散状态变量xk=(xTyTzT)k,则系统状态方程为
xk+1=f(xk)+wk
(3)
式中:f(·)为状态转移函数;wk为过程噪声,wk~N(0,Q),Q为噪声协方差矩阵。对于固定目标,f(xk)=xk,Q=0n×n,0n×n代表n×n的零矩阵,n为状态向量的维数。
根据图2,由目标点和无人机之间的位置关系得系统量测方程为
zk=h(xk)+vk
(4)
(5)
其中,vk为观测噪声,vk~N(0,R),且与系统噪声相互独立,R为量测噪声协方差矩阵。
2 平滑变结构-卡尔曼滤波算法
卡尔曼滤波是一种实时性高的最优估计算法,在目标定位方面有着广泛的应用,但在系统受到大扰动或者噪声非高斯分布时,易出现精度下降甚至发散的问题。平滑变结构滤波是一种次优估计算法,其优势是在应对模型不准确和未知噪声时有较好的鲁棒性和稳定性。本文将卡尔曼滤波和平滑变结构滤波进行融合,设计了平滑变结构-卡尔曼组合滤波算法,保持了卡尔曼滤波的精度优势,改善了滤波的鲁棒性。
2.1 平滑变结构滤波
SVSF算法基本思想是,通过使用SVSF增益,将估计状态限制在存在子空间内,沿着真值轨迹来回切换,如图3所示。

图3 平滑变结构滤波示意图Fig.3 Schematic diagram of smooth variable structure filter
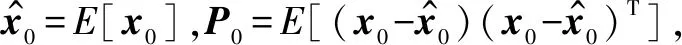
首先,进行一步预测,即
(6)
(7)
(8)
第二步,求解SVSF增益并进行更新,即

(9)
(10)
(11)

平滑有界层宽度矩阵ψk的定义为
(12)
饱和函数的定义为
(13)
式中,vki表示vk中第i个元素,ψkii为ψk中第i个主对角线元素,二者相除构成饱和运算列向量的第i个元素,i=1,…,s,s为vk的维数。
2.2 平滑变结构-卡尔曼组合滤波
由于1.2节构建的量测方程具有较强的非线性,采用泰勒展开的方式存在截断误差会影响滤波精度,因此,本文采用UKF与SVSF的组合滤波。UKF算法已很成熟,不再介绍。
由式(12)ψk的定义可以看出,其大小直接与系统误差和系统模型有关。因此,可以利用ψk来评判系统当前模型不确定性和噪声大小。为了兼顾卡尔曼滤波的精度,本文设计以切换增益的策略,构建SVSF和卡尔曼组合滤波。当ψk小于预设值ψmin,则当前系统模型较准确、噪声较小,此时采用卡尔曼增益,获取最优估计保证滤波精度;当ψk大于预设值ψmin,当前系统模型不够准确、噪声较大,则采用SVSF增益,获取次优估计保证滤波稳定性。组合滤波流程如图4所示。其中,ψmin为经验数据,可利用统计学方法从历史数据中获取。
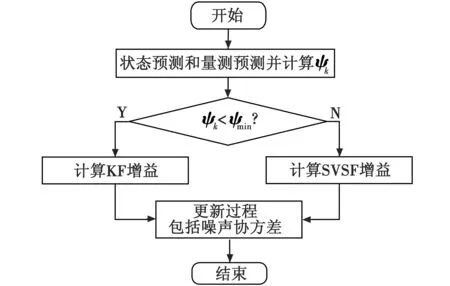
图4 平滑变结构-卡尔曼组合滤波流程图Fig.4 Flow chart of SVSF-KF
在计算量相当的情况下,UKF的无迹变换(UT)的结果比泰勒展开的近似更为准确。因此,对组合滤波预测阶段统一使用UKF的方法,式(6)~(8)可变为
(14)
(15)
(16)
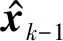
同时,为了提高平滑有界层宽度计算精度,将UKF量测协方差代入式(12)得
停药反跳:服用氢化可的松、强的松等治疗风湿、类风湿性关节炎时,吃维生素E既可助激素一臂之力,增强疗效,又可防止和减少激素撤停时疾病“反跳现象”的发生。
(17)

(18)
SVSF增益及量测更新仍按照式(9)~(11)计算。当采用UKF增益时,则按照标准UKF算法计算。
2.3 基于残差自适应的组合滤波方法
在组合滤波算法中,无论是采用SVSF增益还是UKF增益,Rk都将影响增益大小,在先验估计不准确的情况下,会造成滤波精度下降甚至发散。因此,需对噪声协方差矩阵进行实时在线调整,使噪声协方差矩阵可以根据系统状态进行自适应调节。
根据已有文献可知,在Qk和Rk非同时变化时,可以利用新息或者残差序列对Rk进行实时估计[12-13]。文献[12]利用新息序列实现了对量测噪声的实时跟踪。然而,此方法存在两项相减,可能会使Rk失去正定性。参考文献[13],本文使用残差序列对Rk进行在线估计。
由残差定义,根据开窗估计法和误差传播理论,可得卡尔曼滤波Rk的在线估计为
(19)
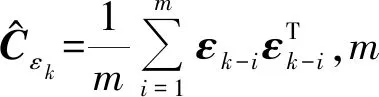
Pk=Pk|k-1-KPzzKT
(20)
式中,K为UKF增益。
将式(18)和式(20)代入式(19),得组合滤波算法Rk的实时估计为
(21)
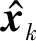
3 实验验证
3.1 第一组实验:大扰动情况
第一组实验主要验证算法在系统受到大扰动情况下的性能。实验基本条件设置为:静止目标真实位置为(350 m,450 m,8 m),无人机在发现目标后,盘旋上升飞行,飞行半径r=100 m,圆心坐标为(500 m,600 m,400 m),初始航高为400 m,盘旋飞行角速度为0.02 rad/s、上升速度为1 m/s,无人机自身定位误差服从均值为0°、标准差为5°的正态分布,无人机绕飞一周,均匀选取180个采样点。系统方程如式(3)和式(4),Q矩阵为零矩阵,R=diag(1,1)。目标初始状态估计为(330 m,480 m,0 m),初始状态协方差设置为P0=diag(100,100,100)。
实验1参数设置:视轴角噪声与估计模型一致,未受到扰动,整个测量过程中,视轴角误差服从均值为0°、1倍标准差的正态分布。
实验2参数设置:视轴角噪声与估计模型一致,但受到了大扰动,在120~150采样点时间段内,视轴角标准差由1倍变为3倍,其他设置与实验1相同。
实验3和实验4参数设置与实验2参数设置基本相同,将大扰动时间段内测量标准差由3倍分别变为4倍和5倍,以检验不同扰动强度下算法性能。
实验采用均方根误差(RMSE)衡量目标定位的精度。为了验证算法的性能,每个实验进行1000次蒙特卡罗实验,每次实验参数相同。RMSE定义如下
(22)
式中:(x′k,y′k,z′k)为第k次目标位置估计值;(xT,yT,zT) 为目标真实位置。
仿真结果如图5和表1所示。通过图5和表1可以看出,在噪声模型估计准确、未受到大扰动的情况下,在180个采样点时间内基本稳定收敛,3种算法的滤波效果相近,都有较高的精度。在增加了大扰动的情况下,各算法都有一定的精度下降。3倍噪声扰动时UKF和AIUKF的鲁棒性也可以使滤波保持较高精度,但随着扰动增大,卡尔曼滤波鲁棒性下降;本文算法在5倍正常噪声下,精度下降仅11.89%,其他2种算法都超过了50%,这是因为UKF和AIUKF在受到大扰动的情况下,仍然是假定噪声统计特性没有变化,所以精度下降较多;AIUKF由于迭代时仍然将大扰动影响的测量作为正常噪声的测量值,使得偏差更大,所以精度下降最快;本文算法能够对噪声进行在线识别,同时,SVSF增益直接与模型的不确定性、量测噪声水平有关,在受到大扰动时,能够将估计值限定在真实值存在子空间内,所以,依然有较高精度。
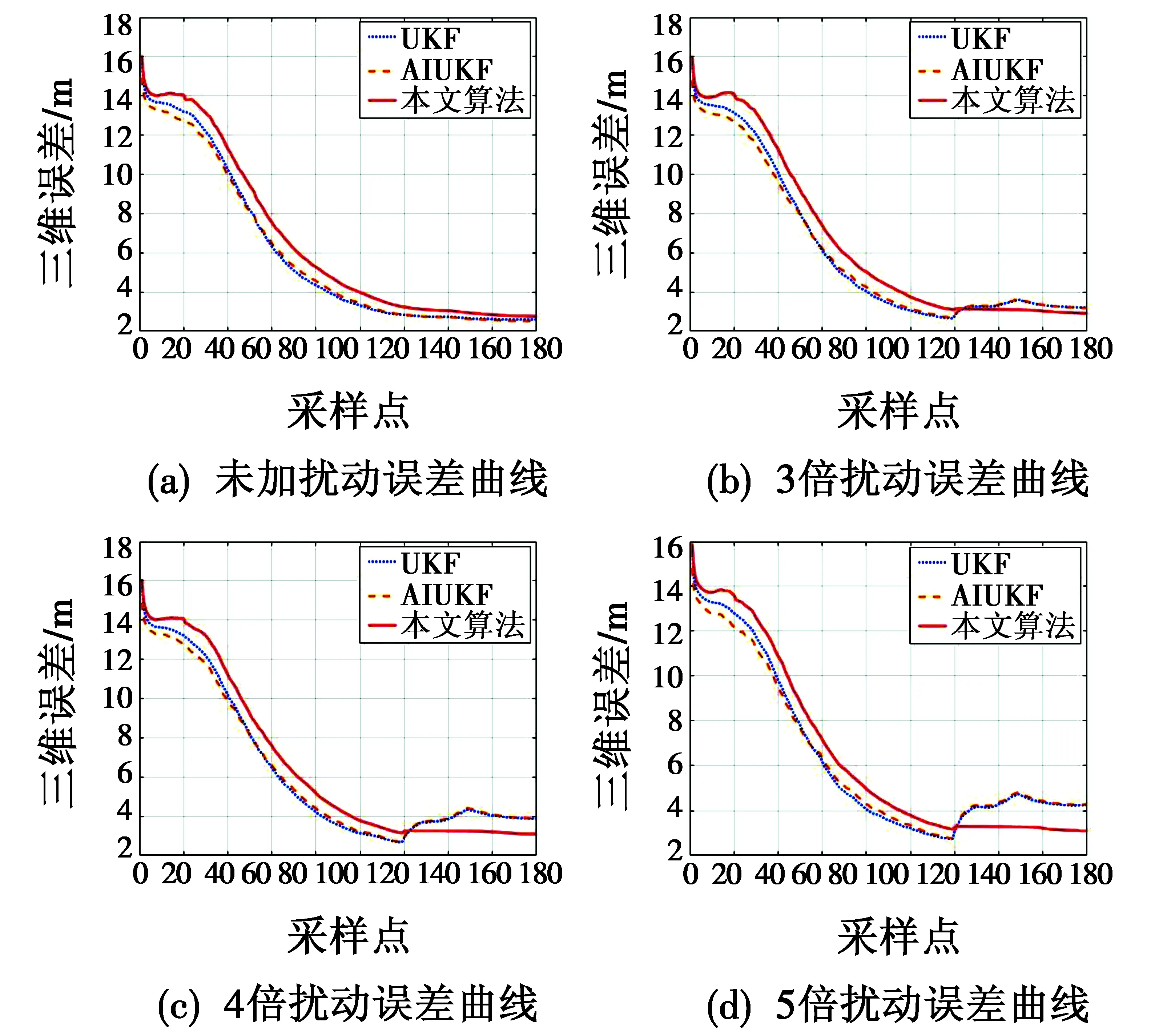
图5 不同扰动下误差曲线Fig.5 Error curves under different disturbances
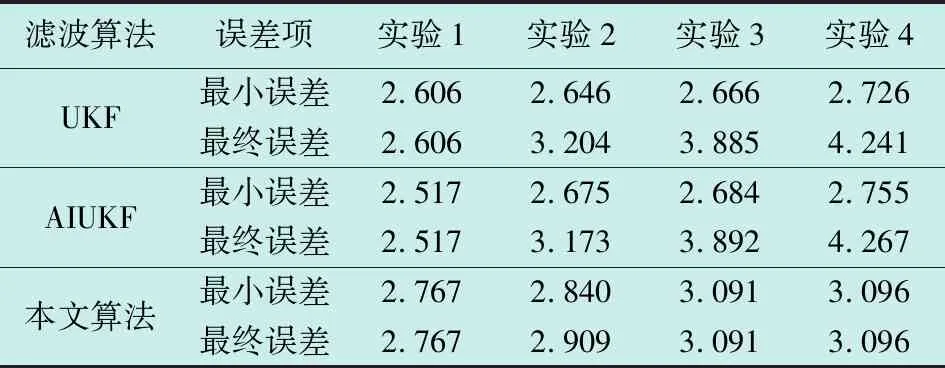
表1 不同扰动下定位精度Table 1 Accuracy under different disturbances
3.2 第二组实验:噪声模型估计不准确情况
第二组实验验证算法在噪声模型估计不准确情况下的性能,以第一组实验1收敛结果为对比基准。实验基本设置同第一组实验,采样间隔不变,飞行时间增长,采样点增加到400个,量测噪声服从以下非高斯分布
vk~(1-μ)N(0,R)+μU(0,1)
(23)
式中:μ为因子系数;N(0,R) 表示均值为0、协方差矩阵为R的正态分布;U(0,1) 表示0~1之间的均匀分布。
实验中μ设置为0.35,同样进行1000次的蒙特卡罗实验,每次实验参数相同,实验结果如图6所示。

图6 非高斯分布噪声滤波效果Fig.6 Non-Gaussian noise filtering
通过1000次蒙特卡罗实验,本文算法定位误差为稳定在2.95 m左右,而另外2种算法则呈现了发散的趋势。
在噪声满足高斯分布的情况下,卡尔曼滤波器随着观测数据的增多,会得到越来越精确的结果。但是在噪声不满足高斯分布时,卡尔曼滤波器仍然以处理高斯噪声方式进行滤波,必然会产生估计误差,其影响程度由系统误差决定,并且会累积,最终导致滤波发散[14]。而本文算法使用平滑有界宽度ψk度量系统误差状态,它不仅包含状态向量预协方差、量测先验误差,还包含量测转移矩阵、量测后验误差和收敛率等。本文算法使用两种增益:一方面使得估计状态始终在真实状态轨迹周围,保持了鲁棒性;另一方面利用了卡尔曼最优估计的特点取得较高精度。
4 结束语
本文介绍了小型无人机测向交叉目标定位原理和滤波模型建立,分析了基于卡尔曼滤波算法的优势和不足,针对卡尔曼滤波对噪声分布要求高、鲁棒性差的问题,本文提出了一种卡尔曼和平滑变结构组合滤波算法。利用仿真实验,在不同噪声情况下,进行了对比验证。实验表明,本文算法具有良好的精度和鲁棒性,具有一定的工程参考价值。下一步,将利用无人机进行实际飞行验证算法性能,并将其扩展到移动目标定位中。

