基于Kalman滤波和APNN的卫星网络节点故障定位方法
邵烨荣
(广州工商学院 计算机科学与工程系, 广州 510850)
1 引言
随着通信技术的发展,人造卫星在现代生活中发挥着越来越重要的作用。与地面网络相比,卫星通信具有技术要求高、成本高、维护难度大、维护难度大等特点,一旦卫星发生故障,所造成的损失就异常巨大,因此,卫星通信是国家基础服务、抢险救灾、军事应用等最方便可靠的通信手段。卫星故障的定位及时准确,预测故障发生,对保障卫星功能及服务质量具有关键作用。
卫星网络是借助卫星转发器中继信号的能力完成其各个节点之间数据传输的网络,为世界各地的用户提供了覆盖全球范围的网络访问服务。对卫星网络来说,通信是它最重要的特征和最核心的功能,通信能力可以表现出各种故障引起的症状,因此对于卫星网络的故障定位,主要是针对卫星网络节点的故障定位。
目前许多相关领域已经充分认识到卫星网络节点故障定位的重要性,如江文建等研究基于ILLE和SVM的卫星执行机构系统故障检测与定位方法,以某高指向精度卫星平台为研究对象,采用增量式局部线性嵌入(ILLE)和支持向量机(SVM)相结合的方法,研究了多组磁力伺服卫星执行机构的故障检测和故障定位技术。在分析执行机构故障模式和故障影响的基础上,利用支持向量机(SVM)方法,实时提取和更新卫星姿态控制系统的高维故障信息,进行降维和特征提取,实现了执行机构系统故障检测,有效地实现了卫星姿态控制系统执行机构故障定位,但是该种方法计算较为复杂,且定位误差较大;邵梦晗等研究INS/GNSS紧组合导航系统故障探测与隔离的改进方法,对于 INS/GNSS紧凑组合,GNSS伪距和伪距率信息的可靠性检验是系统容错设计的关键。现有思想都是以整个系统为基础,对组合卡尔曼滤波器的信息进行χ~2验证。在利用GNSS观测信息前,加入一个故障检测和隔离模块,并采用了结合w-检测法和χ~2检验法识别故障。该方法与单纯的χ~2检测法相比,实现了故障星的定位和选择可靠的伪距组合,有效地保证了后续滤波结果的可靠性。对于 INS/GNSS紧凑组合,GNSS伪距和伪距率信息的可靠性检验是系统容错设计的关键。该种方法容错性强,但产生的通信负载较大效率低。
为解决目前研究方法存在的问题,本文提出基于Kalman滤波和APNN的卫星网络节点故障定位方法,创新点主要是使用Kalman滤波和自适应概率神经网络(adaptive probabilistic neural network,APNN)相结合的方法对卫星网络节点故障进行定位,以便科学、快速地发现和处理各种故障问题。
2 基于Kalman滤波和APNN的卫星网络节点故障定位方法
2.1 基于Kalman滤波的故障状态估计
可以通过Kalman滤波算法完成信号追踪功能,该算法可估计真实的故障状态,若想获得和原状态近似度较大的故障状态估计结果,应让估计均方误差达到最小。
∈表示定义离散时间过程的原始状态变量,其时间过程描述为:
=x-1+
(1)
∈表示定义的观测变量,其量测方程描述为:
=x+
(2)
式(1)~(2)中:表示时刻的卫星网络节点故障状态;上一时刻故障状态变量-1对这一时刻故障状态变量的增益,假如是常数(实际或许随时间变化),用×阶的系统矩阵表示;表示时刻的测量值;故障状态变量对测量变量的增益,假如是常数(实际或许随时间变化),用×阶的观测矩阵表示;表示过程噪声,表示观测噪声。、两者都是随机信号,将它们设置成互相独立,且正态分布的高斯白噪声,定义分别描述为:
()~(0,)
(3)
()~(0,)
(4)
式(3)~(4)中,和分别表示过程噪声协方差矩阵和观测噪声协方差矩阵。为了让滤波器获取更好的性能,可改变和的值来实现。
在已知先前的测量变量时,的先验估计的概率分布决定了的更新,此过程基于贝叶斯规则完成。式(5)描述了得出离散时间过程的故障状态变量,即:
=+(-x)
(5)
式(5)中:表示已知第步之前状态时第步的先验状态估计;表示已知测量变量情况下第步的后验状态估计;是×阶矩阵,被叫作Kalman增益或混合因数。从式(5)可得,后验状态估计是由先验估计和加权的测量变量及其预测x之差的线性组合组成的。
矩阵中元素计算过程为:
=+(+)
(6)
式(6)中,表示通过卫星网络节点故障状态推导出的时刻误差协方差矩阵。
最终的Kalman滤波算法变成含有数值解的预估校正算法,所求最优的故障状态变量估计值为滤除卫星网络中的干扰后的数值解。
2.2 基于自适应概率神经网络的卫星网络节点故障定位
对2.1节获取的最优故障状态变量估计值实施归一化处理,蜂群算法把自适应概率神经网络的样本误差函数看作是一组寻找最佳平滑因子集的适应函数算法,通过多次迭代近似得到最优解集。自适应概率神经网络把最优解集作为一组光滑因子,应用于卫星故障诊断系统中,图1描述了该算法改进流程。

图1 自适应概率神经网络的流程框图
该算法的详细操作流程描述如下:
1该算法考虑了蜂群算法中蜂群的规模,算法迭代次数最大值,优化参数所包含的维数,光滑因子集以及蜜源的初域,分别初始化为n、Max、故障类型的总数、蜜源和[0,2]。
2目标函数被视为样本误差函数,具体如式(7)所示,表示概率神经网络(probabilistic neural network,PNN)的分类结果,表示训练数据原始的对应结果,表示输入样本。
=(-)
(7)
3变化目标函数可以得到适应度函数,原因是将目标函数视为样本误差函数,是求解最小值的问题,适应度函数的表达式为:
=11+
(8)
4在蜜源周围,引导蜂需要在蜜源附近寻找新的蜜源,如果新蜜源的适应度要好于原蜜源,则计算新蜜源的方位,以表示[-1,1]之间的随机值,以表示当前个体的蜜源位置,以表示任意一个领域个体的蜜源位置,如果不满足上述条件,那么未更新计数加1。
5训练自适应概率神经网络可采用步骤2处理后的数据实现,适应度函数的值就是获得训练数据的误差值。
6对新老蜜源进行适应度比较。当新的蜜源的适应度大于旧的时,用新的蜜源代替旧的蜜源;如果不满足上述条件,则旧蜜源维持不变。
7通过步骤6,跟随蜂可得到适应度函数值,根据适应度的值对概率进行计算,式(9)描述其计算过程,蜜源可跟随概率高的蜜蜂进行找寻。
=×
(9)
8在连续搜索过程中,蜜源对数值更新的次数有一定的限制,如果数值在限定的次数内未更新,则该蜜源将被引导蜂自动放弃而变成侦察蜂,并可以通过侦察蜂使用随机算法生成新的蜜源位置。
9运用优化好的APNN实现卫星网络节点故障定位。
2.3 Kalman滤波和自适应概率神经网络融合的卫星网络节点故障定位
为了保证卫星网络节点故障精准的定位,融合Kalman滤波和自适应概率神经网络采用阈值计算,对卫星网络节点阈值进行计算,获得阈值具有较高的可信度,计算公式为:
=×ln
(10)
式(10)中:表示卫星网络节点的强度;表示卫星网络节点的数量。为了对阈值进行分层获取,需要改进阈值,归一化处理后计算如下:
=×ln(-1)
(11)
式(11)中,表示分解层数。Kalman滤波和自适应概率神经网络融合的卫星网络节点故障定位中,定位公式为:
=××
(12)
式(12)中:表示卫星网络节点故障定位中相邻点之间距离的误差;表示相邻点之间的距离。归一化处理通过Kalman滤波算法获得的最优故障状态变量估计值,处理后的数据被用于自适应概率神经网络的训练集中,完成Kalman滤波和自适应概率神经网络融合的卫星网络节点故障定位。
3 实验分析
为验证本文所提方法的卫星网络节点故障定位性能,以采用MATLAB软件仿真的卫星网络为实验对象,其中包含2层卫星星座,分别为高轨道地球卫星(GEO)和低轨道地球卫星(LEO),并利用近似随机均匀分布的算法设置卫星节点的故障,卫星星座参数如表1所示。

表1 卫星星座参数
结合表1卫星星座参数,进行仿真实验,实验过程如下:
1仿真设计便携式卫星网络节点装置,设置天线,确定方向变化;
2开启便携式卫星网络移动台通讯网络模式;
3结合手机共享便携式卫星网络节点装置,建立语音通话平台,对卫星网络节点故障传输数据进行提取;
4将手机放置在一个地方,平均10 min改变一次天线方向;
5记录好不同方向下的卫星网络节点故障变化数据。
3.1 故障定位正确率对比
实验分析不同故障数量下卫星网络节点故障定位的正确率,并设计对比实验,选取文献[6]基于ILLE和SVM的卫星执行机构系统故障检测与定位方法和文献[7]INS/GNSS紧组合导航系统故障探测与隔离的改进方法,作为本文方法的对比方法,对比结果如图2所示。

图2 故障定位正确率直方图
由图2可得,故障定位的正确率随着故障数量的增加而降低,在故障数量较少时,3种方法之间的正确率差距较小,均保持在80%以上;在故障数量上升至50%时,3种方法之间的正确率差距开始变大,尤其是达到70%时,文献[6]方法的正确率呈大幅度下降,稳定性差。相对于其他2种方法,本文方法的正确率下降趋势平稳,且始终高于95%,基本不受影响。由此可见,本文方法对卫星网络节点故障定位具有较高的准确性和稳定性,可大大提高卫星网络节点故障定位的效果。
3.2 故障定位完全率对比
实验分析卫星网络节点故障定位的完全率和故障数量之间的关系,实验结果如图3所示。

图3 故障定位完全率曲线
由图3可得,故障数量为0时,3种方法的故障定位完全率相同,随着故障数量增加,完全率均有所降低。当故障数量较少时,3种方法的完全率较为接近,当故障数量达到40%时,文献[6]方法和文献[7]方法的完全率下降趋势明显,尤其是文献[7]方法,当故障数量达到70%时,完全率已低于40%。相对于其他2种方法,本文方法的完全率受故障数量影响程度较小,始终保持最高,且变化平稳。对比这些数据可以看出,本文方法在保证较高故障定位正确率的同时,还能获得较高的故障定位完全率,优势极其显著。
3.3 故障定位通信开销对比
实验分析3种方法在不同故障数量下卫星网络节点故障定位的通信开销,实验结果如图4所示。

图4 故障定位通信开销直方图
由图4可得,文献[6]方法的故障定位通信开销不会随故障数量的增加而增加,基本趋于平稳,而文献[7]方法的通信开销随故障数量的增加而减小。相对于其他2种方法,虽然本文方法的通信开销随着故障数量的增加有增加趋势,但其增长幅度很小,且通信开销始终保持最低。由此可以看出,本文方法的通信负载较小,可提升卫星网络节点故障定位的效率。
3.4 故障定位时延对比
实验分析不同故障数量下,卫星网络节点故障定位的时延,实验结果如图5所示。
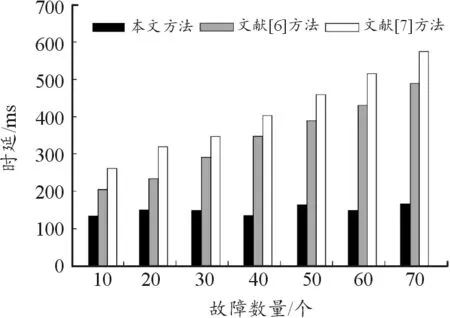
图5 故障定位时延直方图
由图5可得,文献[6]方法和文献[7]方法的故障定位时延都随着故障数量的增加而增大,且文献[7]方法的时延始终保持最高。和其他2种方法相比,本文方法在进行故障定位时带来的时延要小很多,并且故障数量的增加对其基本没有影响。对比这些数据可以看出,在不同故障数量下,本文方法具有较高的定位效率,可进一步提升卫星网络节点故障定位的效果。
3.5 故障定位均方根误差对比
均方根误差(root mean square error,RMSE)表示误差的统计学特性即离散特性。实验根据RMSE分析卫星网络节点故障定位精度,实验结果如图6所示。

图6 故障定位均方根误差曲线
由图6可得,3种方法起始时间的定位误差值相同,当进行到4 s时,定位误差值均处于较低状态,进行到6 s时,文献[6]方法的定位误差值上升最快。相对于其他2种方法,本文方法的定位误差值始终保持最低,且在5×10以下,波动较弱。由此可见,随着时间增加,本文方法定位卫星网络节点故障具备较高的精度。
综上所述,本文方法的故障定位正确率、完全率较高,故障定位通信开销、时延较短,其原因是本文方法使用Kalman滤波和自适应概率神经网络相结合的方法对卫星网络节点故障进行定位,一定程度上能够科学地、快速地发现和处理各种故障问题,有利于卫星网络节点故障精准定位。
4 结论
为了及时发现并定位卫星网络节点故障,提出基于Kalman滤波和APNN的卫星网络节点故障定位方法,该方法主要使用Kalman滤波和自适应概率神经网络相结合的方法,实现卫星网络节点故障定位,提高定位的准确性和完全性,减少卫星网络运行成本,降低由于卫星网络节点故障所导致的损失和影响。以后,需要进一步完善该研究方法,使其更好地应用于卫星故障诊断系统,为通信行业的发展贡献力量。

