低复杂度FIR 滤波器NR-SCSE 优化设计
李 成,郭 涛,石 帅,畅彦祥
(1.中北大学仪器科学与动态测试教育部重点实验室,山西太原 030051;2.中国航天科技集团有限公司中国运载火箭技术研究院,北京 100000)
在工程领域发展趋势中,如数字医学中心电信号处理[1]、实时应用的嵌入式系统[2]、软件无线电和通信中数据大规模输入、输出等[3],对数字信号处理系统的要求越来越高。数字滤波器作为数字信号处理系统的主要处理部件,其性能直接决定了系统的信号处理能力。与无限冲激响应滤波器相比,有限冲激响应(Finite Impulse Response,FIR)滤波器具有很强的稳定性和严格的线性相位特性,得到了更广泛的应用。但是FIR 滤波器的乘法器增加了系统的功耗和硬件复杂度,限制了FIR 滤波器的发展。因此,FIR 滤波器的低功耗设计成为提高整个系统信号处理效率的重点。目前主要的方法是降低硬件复杂度和优化滤波器系数。对于滤波器系数优化,文献[4]中采用规范有符号数字(Canonical Signed Digit,CSD)编码来最小化滤波器系数中非零元素的个数,从而实现滤波器的结构优化。文献[5]在CSD 码的基础上设计了一种转换器,提高了二进制数转换为CSD 码的速度。文献[6-7]采用基于CSD 编码的遗传算法优化滤波器的设计,文献[8]采用花粉授粉算法结合公共子表达式消除(Common Subexpression Elimination,CSE)进一步提高了加法器的效率,实现了无乘法器设计。
在乘法器优化方面,针对快速傅里叶变换中乘法运算多、内存占用率高,通过设计CSD 乘法器对其进行优化[9-11]。在图像处理系统中,使用CSD 编码优化离散余弦系统中的乘法运算[12-13]。文中基于CSE算法和CSD 编码,提出了一种低复杂度FIR 滤波器的设计方法。
1 基本原理和模型
1.1 滤波器原理
FIR 滤波器输出Y(n)为输入序列X(n)与单位取样响应h(n)的线性卷积,输出表达式与系统函数分别为:
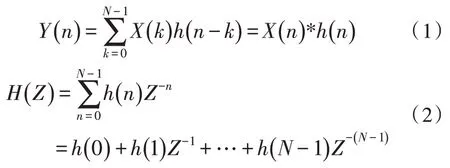
式中,N为FIR 滤波器的阶数,根据上式可以得出FIR 滤波器的直接型结构[14],如1 图所示。
根据图1 的结构,对于N阶FIR 滤波器,总共需要N个乘法运算、N-1 个延时单元和一个N输入的加法运算。在通常情况下,相较于加法和移位运算,乘法运算会耗费更多的硬件资源,故需要把设计中的乘法器转换为移位加法器。

图1 FIR滤波器直接型结构
1.2 规范有符号数编码
CSD 编码作为一种三元编码方式,不同于二进制编码,它具有{1,0,-1}三元值(文中用代替-1),其基本原理是尽量减少乘法器中的非零元素,减少移位和加法次数,从而降低了乘法器的硬件复杂度。将二进制编码转化为CSD 码的具体实现方法:二进制数码从最低的有效位开始,将大于2 的1 序列全部替换为10,…,0,并将1011 替换为1 10;最后从最高有效位开始,用011 代替10[15]。最佳的CSD 编码方式可以减少非零元素的数量,降低资源消耗,缩短计算时间。其特点有:
1)在一个CSD 数据里,没有两个连续的非零位;
2)CSD 数据是所有数字表示法里所含非零位数最少的一种;
3)二进制数码与CSD 码一一对应。
1.3 CSE算法
滤波器初始系数组可表示为向量组h=[h(0)h(1)…h(N)]T,将向量组h中的每个系数按照1.2 里的步骤转化为CSD 码,得到新的系数向量组hC,其中第i个系数向量
在系数hC(i)中,若存在与为非零量,且中间量全都为0(中间有w个0),则称这个多项子式为w阶2 项子式。如果与同号,则称该子式为2 项偶子式,例如1001,00;反之,与异号,则称该子式为2 项奇子式,例如100,001。若系数向量hC(i)中只含有一个非零元素,无法构成任何2 项子式时,如0010,则称hC(i)为孤子。
CSE 算法的基本原理是在系数向量组(即公共表达式)中找到两个相同阶次的项,并计算出输入信号与公共表达式相乘的结果,使不同的位置和系数共享结果,减少运算单元数。例如,假设13 位量化系数hC(1)=10010010000,可以看出有2 阶2 项偶子式1001,如果使用通常的移位加法,则需要4 个加法器,如图2(a)所示;采用CSE 算法,则需3 个加法器,如图2(b)所示。

图2 系数hC(1)实现方法
针对CSE 算法的原理,其难点在于如何从系数向量组中高效快速地找出公共子式,文献[16]提出了一种非递归的带符号共同子式消除(Non Recursive Signed Common Subexpression Elimination,NR-SCSE),具体实现方法如下:
子表达式表示为S1 和S2,其中S1 表示2 项偶子式,S2 表示2 项奇子式。每一个系数向量组hC对应一个子式矩阵Pn,元素Pn(i,j)的值为j阶2 项子式出现的次数,i值表示该2 项子式类别(S1 或S2)。例如Pn(1,3)=3 表示3 阶2 项偶子式0 001(或10 00)出现的次数为3。将系数向量组hC写作系数集YCSD,假设系数向量集YCSD如下:

其对应的子式矩阵Pn{1}为:
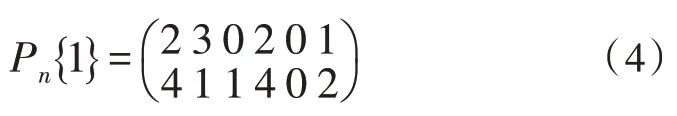
因Pn(2,1)=Pn(2,4)=4 为最大值,此处取01(或10)为第一个公共子式,然后将公共子式对应在YCSD中的数字置零,得到新系数集如式(5)所示:

该滤波器系数集YCSD通过NR-SCSE 算法实现的结构如图3 所示,最终需要的加法器数量为10,相较于直接法,数量减少了4 个。
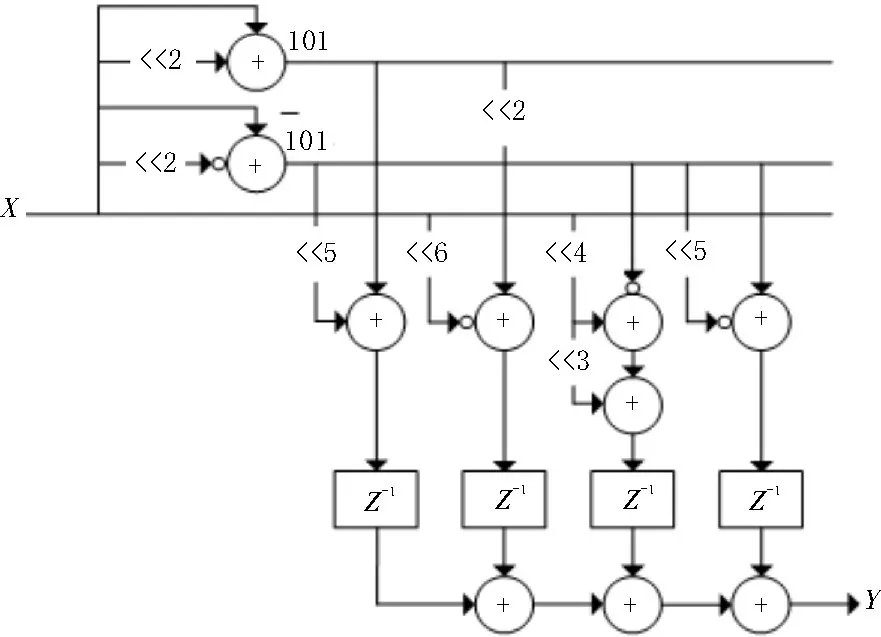
图3 系数集YCSD的CSE实现
2 FIR滤波器设计
2.1 FIR滤波器结构设计
首先,利用Matlab 设计了一个15 阶(长度16 位)低通线性相位FIR 滤波器。窗口函数是Blackman 窗口函数。根据要求设计了滤波器系数,并在FPGA中搭建了FIR 滤波器结构。然后在Matlab 中生成两个不同频率的合成输入信号,在Modelsim 中用滤波器对输入信号进行仿真,对高频分量进行滤波,将低频部分输出,并用Matlab 对输出信号进行分析。
FPGA 在实现FIR 滤波器结构时,主要采用串行结构。首先,将输入数据的每个延迟单元串行相加并乘以相应的系数,将乘积结果累加后输出。因此,整个设计只使用了一个乘法器单元。串行结构有两种形式:全串行结构和半串行结构。由于全串行结构结合了加法器中的对称量化系数运算,与半串行结构相比,加法器的数目可以减少一半,因此采用全串行结构。同时根据第一节中的内容,使用移位加法运算取代乘法运算,将乘法器移出设计。全串行FIR 滤波器结构如图4 所示。

图4 全串行FIR滤波器结构
从图中可以看出,系统时钟通过1/8 分频器获得分频时钟,控制数据输入,使输入数据以1/8系统时钟频率存储在移位寄存器中,使一个加法器在一个系统时钟周期内完成8 次加法运算。经过量化、CSD 编码和NR-SCSE 优化后,滤波器的原始系数转化为新系数表,然后与加法结果进行移位相加,得到滤波输出。
2.2 滤波器系数量化
FIR滤波器主要参数:截止频率为500 Hz,采样频率为2 000 Hz 的16 阶FIR 低通滤波器。利用Matlab工具箱设计出满足指标的FIR 滤波器,系数的量化位数为12 位,输入数据位宽为12 位,输出数据位宽为29 位,系统时钟为16 kHz。将滤波器系数进行量化取整,并转换为CSD 码如表1 所示。
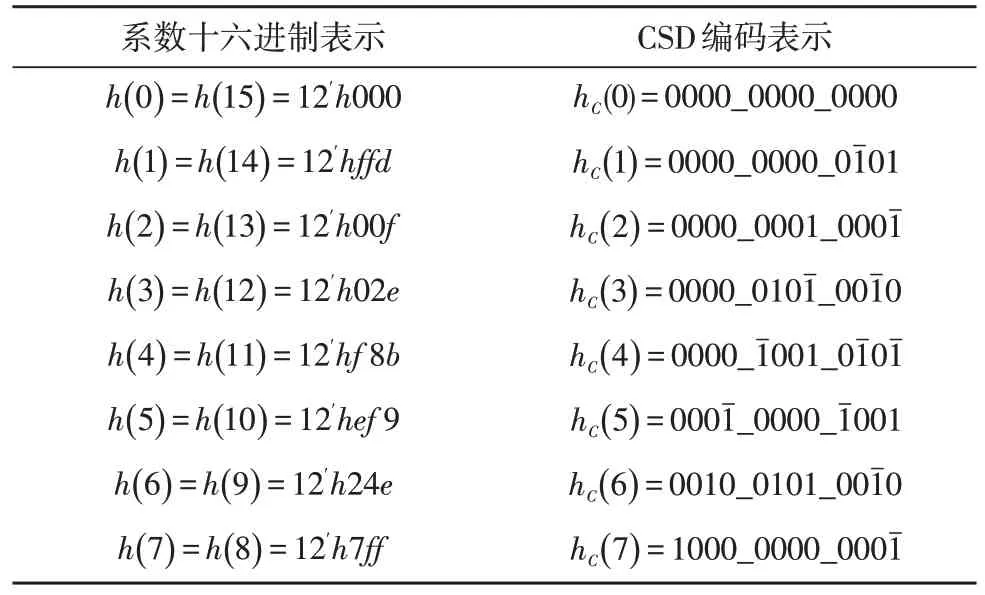
表1 FIR滤波器系数表示
由表1 可得FIR 滤波器量化系数向量组,根据前文提出的NR-SCSE 算法,取001(或100)、1001(或00)为两个3 阶2 项公共子式进行优化,加法器数量从14 个减少至10 个,效果明显。
3 仿真分析
采用Matlab 生成200 Hz 和800 Hz 的合成输入信号源,在Modelsim 中使用优化后的FIR 低通滤波器处理该信号,对800 Hz 的高频部分进行滤波,得到200 Hz 的低频正弦波。利用Matlab 对输出结果进行了分析。最后对输入、输出数据进行了频域和时域分析,最终结果如图5 所示。结果表明,FIR 低通滤波器具有良好的性能。

图5 输入输出信号对比
为了更好地体现出CSD 编码结合NR-SCSE 技术在优化乘法运算中的优势,分别以两种方法设计32、64、128 阶的低通FIR 滤波器,进行对照比较,其结果如表2 所示。相较于乘法直接实现,优化NRSCSE 资源减少率约为30%,并随着阶数的增大,优化效果也越好,有效降低了加法器的数量,改善了滤波器性能。

表2 FIR滤波器两种算法性能对照
4 结论
文中提出了一种无乘法器的低复杂度FIR 低通滤波器。其将公共子表达式消除与CSD 编码相结合,用移位加法代替滤波器中的乘法单元,有效降低了设计的硬件资源。仿真结果表明,与传统的FIR滤波器设计方法相比,加法器的数量可以减少约30%,滤波器的复杂度降低。

