基于多目标和MPEC 的发电市场化电量确定方法
陆昭杨,丁剑鹰,荆朝霞,朱继松
(1.华南理工大学电力学院,广东广州 510640;2.广东省能源集团有限公司经营管理部,广东广州 510630)
自2015 年我国发布《关于进一步深化电力体制改革的若干意见(中发〔2015〕9 号)》[1]以来,中国第二轮电力市场化改革已逐步深化,并已采取了许多改革措施。电力市场改革改变了电网公司的收入模式,这将对其收入产生巨大影响。由于计划电价相对价格较高的特性,可以在一定程度上保护发电机组或发电的利益。考虑到中国电力市场建设的市场机制不完善,计划的电力不能直接完全地市场化交易[2]。电力市场化改革不是一夜之间完成的,而是需要经历一个安全的过渡过程。
在电力市场建设的过程中,有必要不断增加市场交易量,最终实现竞争环节的全面开放[3]。当前,增加电力市场交易量的途径主要是提高发电计划的自由化程度。对于电网公司来说,改进发电计划意味着更多的计划发电成为电力市场的交易目标。当总消耗量固定时,将导致电网通过统一购销电力获得的利润越来越少。电网公司根据政府具体的发电计划,制定了当年的详细发电计划,并明确了每个机组的市场用电量和计划用电量。在制定计划的过程中,电网公司需要考虑高成本单位的市场生存能力。在上述背景下,同时又要考虑自身利益和高成本单位利益的最大化,电网公司很难实现发电计划市场化的目标。当前,根据中国电力市场的实际建设,对电力市场化计划的战略研究非常缺乏。
基于加权和方法,可以将多目标问题转化为单目标函数[4],这个方法易于理解并且较为实用。双层优化是将一个优化问题当做另一个优化问题约束的一种优化方法[5]。
具有等式约束的数学程序[6](MPEC)在能源市场研究中具有广泛的应用,并且是已被证明可以简化复杂问题的解决方法。参考文献[7]中表示了用于每个虚拟电厂(VPP)最佳投标策略的双层模型,其中上层优化目标是最大化单位利润,下层优化目标是社会福利最大化,文中用Karush-Kahn-Tucker(KKT)优化条件替换了作为约束的下层优化。在参考文献[8]中,作者采用基于粒子群优化(PSO)和数学编程的迭代方法,获得了解决复杂双级问题的方案。在参考文献[9]中,作者将决策者的决策方案作为上层优化问题,将电力市场清算模型作为下层优化问题,并通过求解双层模型来获得最优决策。值得关注的是,使用MPEC 方法将下层的市场清算模型转换为一系列约束,然后将这些约束与上层模型结合起来,从而可以用标准形式解决双层优化问题。在参考文献[10]中,热电系统之间的协调通过对日前热市场中热电系统之间的相互作用进行建模来实现,并用奔德斯分解法进行求解。
在上述研究的基础上,该文提供了一种基于多目标和MPEC 的发电计划市场化方法。
1 研究框架和模型
1.1 框架结构
研究框架基于图1 所示的情况。政府机构作为市场化目标的制定者,制定了全面市场化的计划。电网公司实施政府的要求并制定详细可行的市场化计划,这些计划由政府委托给电网公司进行监督并执行。然后,将发电市场化方案作为市场出清的边界,由市场运营机构根据市场成员的报价进行市场出清。作为反馈,市场出清的结果被传回到电网公司,这进一步影响了电网公司的决策。

图1 研究框架示意图
1.2 MPEC数学模型
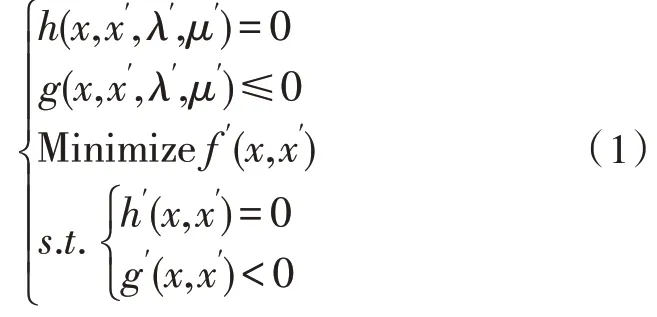
显然,该模型提供了一个嵌套结构,其中一个优化问题(例如上层优化)受到另一个问题(例如下层优化)的约束。优化变量包括两个子集,即上层优化变量x和下层优化变量x′、λ′和μ′。特别地,上层问题取决于所有原始优化变量x和x′,以及下层问题λ′和μ′的对偶变量。
一旦下层的优化问题是凸优化问题,就可以使用KKT 条件替换它们,以简化解决方案,如式(2)~(4)所示:
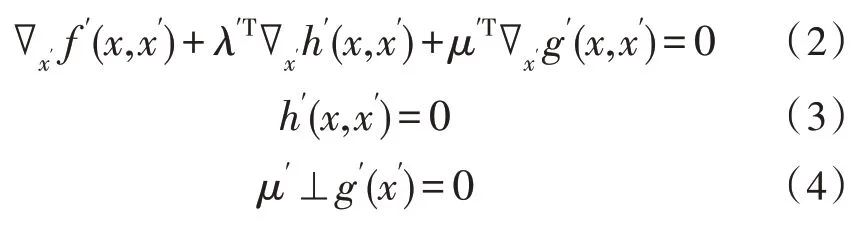
其中,h()和g()分别是等式和不等式的约束表达。
1.3 上层优化
根据以上描述,建立了作为决策者的发电公司的上层优化模型。如式(5)所示,电网公司的优化目标是使高成本单位的收入和出清量的加权和最大化。式(6)、(7)表示优化变量约束。通俗地讲,式(6)表示总的市场化电量应符合政府的要求。同时,每个单位的市场化电量受到式(7)的限制。
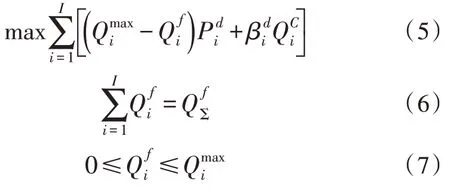
1.4 下层优化
下层优化模型如式(8)所示,市场出清目标是使总发电成本最小化。约束条件包括功率平衡约束如式(9),出清约束如式(10),线路潮流约束如式(11)所示:

考虑到下层优化是凸优化,文中将下层模型转换为一系列KKT 条件[11]。
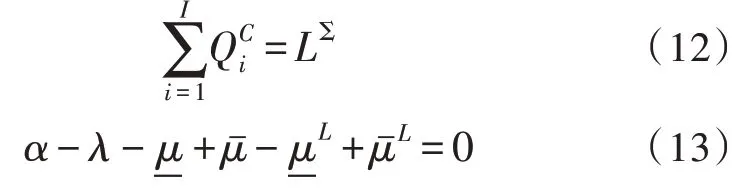
约束条件(10)~(11)被称为互补条件,可以改写为公式(14)~(16),如下:
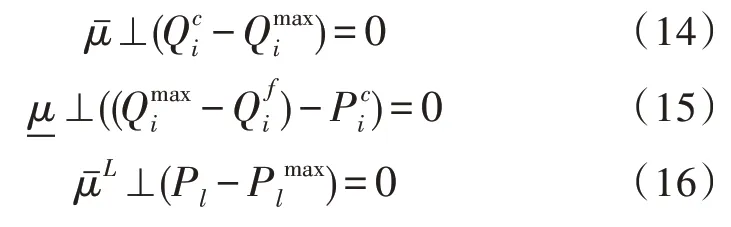
其中,⊥表示互补性。类型一的特殊有序集(Special Ordered Set 1,SOS1)被定义为一组变量,在可行的解决方案中该变量集中不超过一个成员可能为非零。可以使用基于SOS1 的方法来放松互补条件(14)~(16)[12-13]。
2 算例研究
2.1 计算平台
该节基于两个发电机组和3 个节点的简单模型验证了所提出的方法。实验是使用中型家用笔记本电脑(英特尔i5 酷睿双核8 GB 内存)运行代码的。并且该模型由Gurobi求解器(版本9.0.0)[10]求解。
2.2 方案描述和假设
在图2中,两个发电机分别位于节点1(N1)和2(N2)。两个负载位于节点2(N2)和3(N3)。详细地,L2=60 MW,L3=100 MW。图2 中标出了其他一些参数。发电机组G1的最大容量为160 MW,发电机组G2的最大容量为100 MW,发电机组G1的发电成本为α1=0.2 元/kW·h,发电机组G2的发电成本为α2=0.5 元/kW·h,G2被视为高成本单位。用户基准电价为0.7 元/kW·h。线路1的最高容量为65 MW,线路2的最高容量为100 MW,线路3 的最高容量为55 MW。
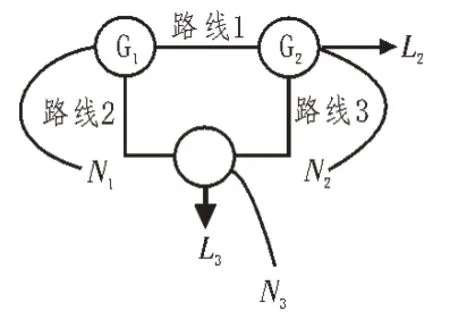
图2 场景示意图
为了便于分析潮流,该文假设3 个分支具有相同的阻抗。以此方式,可以容易地获得用于对传输约束进行建模的功率传输分配因子。
假设政府机构设定的市场化总电量为100 MW·h,则电网公司将采用该文提出的方法进行决策。为了研究参数设置对优化方案的影响,基于和线路传输容量设置了不同的参数组合。这些参数组合如表1所示。

表1 参数组合列表
在方案1 中,两个发电机组受到相同的处理,3 个分支的传输容量受到限制。在方案2 中,通过设置β2>β1,考虑到单元G2的高成本,对单元G2进行特殊处理。3 个分支的传输容量足够大,因此不会发生阻塞。
2.3 结果和分析
优化结果如表2 所示。其中,P1,2,P1,3和P2,3分别表示3 个分支中的潮流。从表中可以看出,在3 种不同的参数配置下,发电的总市场化电量分布在不同的发电机之间,形成了不同的计划电量开放方案。

表2 优化结果
具体而言,在方案1 中,β1=β2,这意味着电网公司对两个机组的市场出清量同样重视。线路1 的潮流处于传输极限,这使得G2的出清电量高于计划的电量,从而使高成本的机组获得一定的市场份额。一般来说,这种情况对于电网公司来说是理想的。在方案2 中,当将β2设置为较高的值时,高成本单元的市场结算价格将比设置为β1时更高。优化结果表明,为较高成本的机组分配了更多的计划容量,但电网公司的收入却大大减少了。在方案3 中,电网中不会存在潮流阻塞的可能性,并且市场更具竞争性。电网公司并未对高成本机组的市场生存给予足够的重视,导致高成本机组的市场份额损失,但电网收入却增加到了8 万元。
以上分析验证了模型的有效性,优化结果合理,可为决策提供参考。
值得一提,对于该文需要增强和完善的方面,使用的示例为简单的人工数据,基于真实数据的仿真分析会更有价值[14]。同时,在现货市场环境下,电网公司不得不应对功率分解曲线问题,这就需要提出解决方案模型来扩展多周期优化模型。
3 结论
为了协调市场改革过程中的多目标问题,对发电计划的市场化问题进行了研究,尝试在MPEC 和加权的基础上,将双层优化模型转化为单层优化模型,将多目标问题转化为单目标问题。总而言之,总结出该文模型具有如下优势:
1)如果没有输电阻塞,则电网公司将优先考虑市场化所有高价电源,以获得最大收益(请参阅方案3)。
2)当电网被阻塞时,根据机组中标量的不同考虑程度采用不同的市场化策略。
3)稍微考虑一下高成本机组生存能力[15],就有一个可执行的方案满足电网约束。同时,它在一定程度上保证了电网的收入(参见方案1)。且认真考虑高成本机组生存能力(请参阅方案2)。
4)根据不等式约束乘数,该方法可以确定在网络潮流中起重要作用的关键机组[16]。

