数据驱动的车载空调设定温度预测研究
胡杰,杨博闻,宋洪干
(1. 武汉理工大学 现代汽车零部件技术湖北省重点实验室,武汉 430070;2. 武汉理工大学 汽车零部件技术湖北省协同创新中心,武汉 430070;3. 新能源与智能网联车湖北工程技术研究中心,武汉 430070)
目前,提高汽车的安全性、舒适性以及优化人车交互已成为智能网联汽车的主要研究方向之一[1]。
在智能网联汽车中,车载空调作为调节车内环境舒适性的不可或缺的汽车总成,其性能的优良和功能的多样已成为汽车品质重要评价指标之一[2],尽管车载空调已经具备一定的智能化,但仍然需要人们对设备的操作做出决策,因此,使用T-Box来通过收集用户的使用习惯和偏好大数据,然后帮用户做出决策的研究就显得非常有意义。
车载空调智能温度调节是改善车内舒适度重要途径,如何确定最佳车内温度是一个问题;张载龙与茹亮[3]提出了一种基于BP神经网络的冷藏车温度预测方法,用一种自适应的学习速率解决了BP神经网络在训练过程收敛速度慢的问题,并实现了车内温度非线性时间序列的预测;翁建华等[4]采用热网络法对车内温度进行预测。太阳辐射是影响车内温度的主要因素,此外车内外表面对流换热和天气状况也有一定影响;刘荣等[5]为实现模型在高纬度大样本下的快速训练,采用移除上边界约束条件的快速支持向量机算法,并基于粒子群优化算法,构建动力电池温度预测模型,实现了温度预测模型的全局最优和群体泛化;殷青等[6]采集某高校建筑实测环境数据,考虑室内外温度时序性和滞后性的关系,建立了基于LSTM神经网络的室内温度预测模型,拟合优度为98.7%。综上,目前的研究主要集中在模型算法的改进和考虑更多环境因素来提高模型性能。
本文对车载空调数据进行分析和处理,提出了一种习惯温度预测模型和时间序列温度预测模型双模型耦合的方法来为特定用户建立热舒适模型,该模型用于预测用户预期的空调设定温度。
1 空调设定温度预测问题
本文研究的空调设定温度预测方法是一种基于数据驱动的预测方法,首先车辆产生的数据通过车载终端(T-BOX)采集并上传到车联网云平台,云平台中的数据库负责存储这大量的用户数据;然后,通过平台管理系统将数据导出并在电脑端对数据进行下载,运用数据挖掘与机器学习方法研究用户使用空调的习惯,建立机器学习预测模型。而对于本文讨论的则是在已知每台车使用空调的历史记录的情况下,结合实时的环境状态,预测用户所需的温度,这属于典型的回归问题[7]。为保证模型的鲁棒性,选用平均绝对百分比误差(MAPE)作为评价指标,其公式为
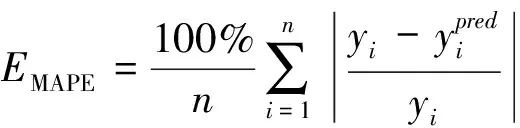
(1)
对于本文用户期望的空调设定温度的预测可以看成是用户习惯温度预测和时间序列温度预测的耦合。对于前者,本文采用机器学习回归预测的方法;而对于后者,本文构造了时间序列特征从而将时间序列预测问题转化为机器学习中的监督学习问题。针对实际应用场景来说就是对于驾驶员上车后开启空调第一时刻的空调设定温度使用习惯温度预测模型进行预测;而对于后面连续性实时空调设定温度则采用时间序列温度预测模型,因此总体用户期望的空调设定温度预测系统如图1所示。
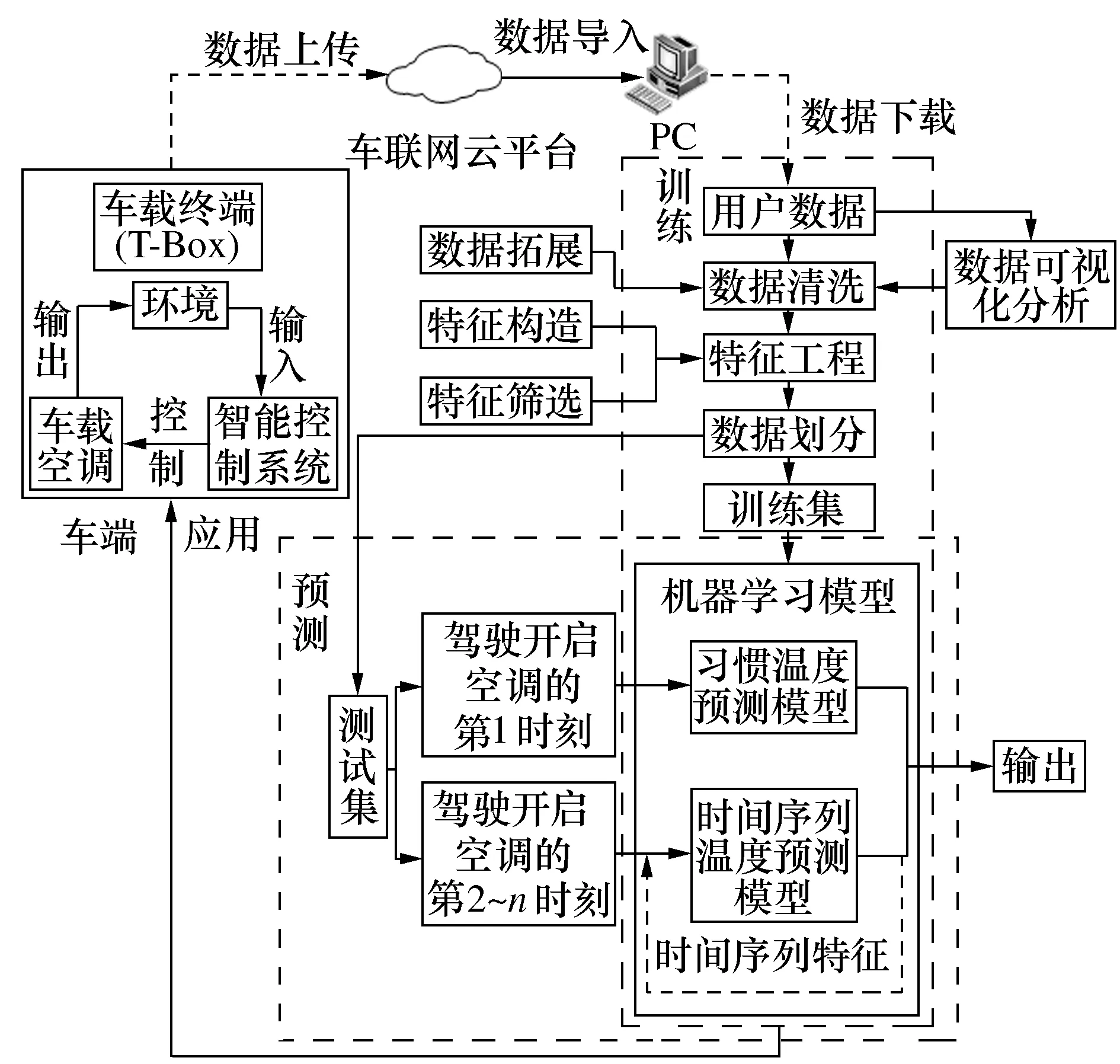
图1 用户期望的空调设定温度预测系统
选取随机森林模型RF作为本文的习惯温度预测模型。而对于时间序列温度预测问题则选择多元线性回归模型Lasso作为的时间序列温度预测模型。根据提出的空调设定温度预测方法,将优化后的RF模型和Lasso模型进行集成,得到RF-Lasso集成模型,从而实现对用户期望的空调设定温度预测。
2 空调设定温度的数据可视化分析及处理
2.1 数据介绍
本文的所有数据均来自于某企业的真实车辆数据,数据格式为Json格式,共七千多万条T-BOX原始数据。包含在2019-01-14到2019-02-28期间1336辆车的T-BOX的记录,T-BOX的采样频率为1条/s。对于空调设定温度预测可能有用的数据进行了提取,共包含13项,分为5大类具体如表1所示。
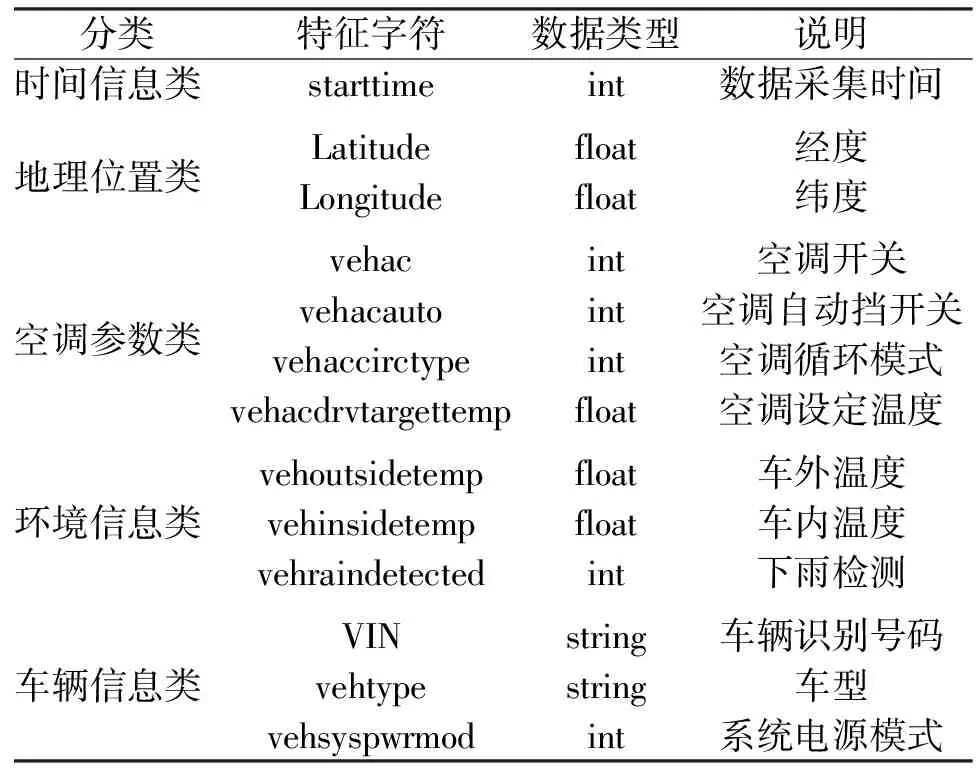
表1 数据名称说明
2.2 数据分析与可视化
1) 地理分布
我国的车辆主要分布在我国中部与东部地区,所以车辆位置分布的热力也集中在这两个地区,由于不同地区的天气差异大,因此可以添加地理特征来提升预测精度。
2) 车外温度分布
通过绘制车外温度分布图如图2所示。图2中可以看出,温度的平均值为7.92℃,标准差为7.57,偏度为0.33,峰度为0.63,呈现近似正态分布其中嵌入的小图为Q-Q图, 纵坐标为特征值,即车外温度的大小,横坐标为正态分布分位数,深蓝色曲线为数据样本,红色直线代表估测结果;如果直线与曲线能够很好拟合,则说明数据样本大体满足正态分布。

图2 车外温度分布图
3) 用户设定的目标温度分布
从用户设定温度分布如图3中可以看出,空调设定温度范围大约是17 ℃~33 ℃。通过对数据进行K-S检验,发现数据近似呈现正态分布并显示渐进显著性。
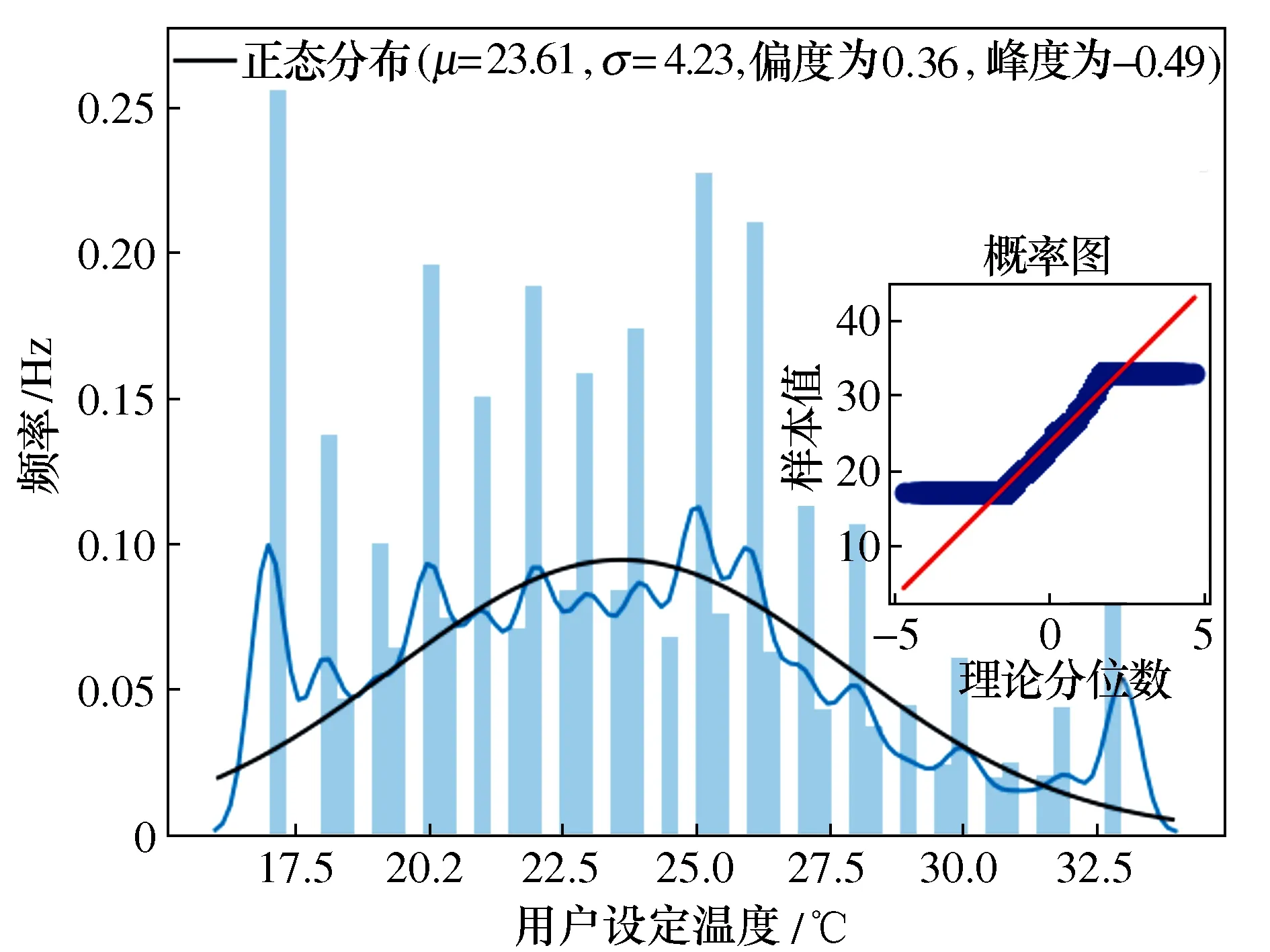
图3 用户设定温度分布图
4) 用户设定温度的变化次数分布
用户设定温度的变化次数分布如图4所示。一般情况下,个人车主一天内调整温度的次数不会过多,而从图中可以明显看出数据存在异常。

图4 空调温度调整次数分布图
5) 用户车辆使用时间天数分布
用户车辆使用时间的天数分布如图5所示。由于原始数据的时间跨度为1月14日到2月28日,共计时间天数46 d,考虑数据量较少的车辆对模型可能会造成干扰,尤其是考虑到个性化推荐的影响,所以对数据少于7 d的车辆给予删除。

图5 车辆使用天数分布图
6) 车外温度传感器和天气温度差值的分布
计算车外温度和天气温度的差值如图6所示。为了剔除温度传感器异常数据的样本,通过图6数据分布的判断,以95%和5%的置信区间去筛选数据,分别得出上下5%的温差数值,差值大于10.5和小于-9.5的视为异常数据,应给予删除,以保证数据样本的可信度和分布合理性。

图6 车外温度与天气温度差值分布图
2.3 数据清洗
通过对数据进行分析发现有以下几种数据故障:
1) 缺失值处理
对于短时间内温度异常的数据采用插值法替换。而对于其他特征,由于采样频率较高且缺失样本数量仅占总样本的0.010 5%,采取直接删除整条数据的方法。
2) 异常值的处理
对于温度类特征异常同样采用插值法进行替换。但是对于周期性跳变式的异常数据,难以保证其他特征是否可信,所以给予整行删除。
3) 样本重采样处理
因为温度变化是一个渐进的过程,短时间内不会骤变,所以数据采样频率为1条/s对于温度预测而言频率过高。为了节省计算时间,重采样的时间间隔取为100 s。
4) 干扰数据样本的处理
通过对调整次数异常的数据车辆进行观察,发现有绝大部分车辆还存在其他数据异常,因此对于这部分车辆的数据全部删除。
3 特征工程
特征工程是在原有数据的基础上提取能体现数据属性的特征,从而提高预测精度。特征工程提取的特征主要包括原始的数据属性特征和在原始数据中提取的新特征,从而更好的对数据进行理解和分析。
3.1 构造新特征
本文根据对数据的理解对原有特征类别做了拓展,并构造了相关的新特征类别,主要分为以下几个部分:
1) 时间信息特征
在原有时间信息特征的基础上提取是否是周末,是否是白天等类别特征。除此之外,一般正常使用空调都有一个调节过程,这样就会有空调的累积运行时间,这对于用户期望的设定温度也有一定的影响。
2) 地理信息特征
本文从原始经纬度地理特征解析出省份、市区、县区3个地理位置特征,并根据我国四大地理分区,将用户车辆的地理位置特征划分成四类,从而提高模型的准确性。
3) 环境信息特征
为了获取更多的环境信息特征,本文通过网络爬虫获取了相关天气特征并根据天气特征可以构造出昼夜温差(diff-temp-daynight)、平均日温(aver-temp)、平均日风速(aver-wind)、天气状况(outside-weather)等特征。由于天气情况种类过多,同理将天气情况根据晴、阴、雨、雪分成4类。
4) 车辆信息特征
在本文中,车辆信息特征有VIN码和车型,假设一名用户仅使用一辆车。由于VIN码和车型都是字符串类型,所以对其进行独热编码,这样对于一个模型来说,一个用户代表一个特征。
5) 人体感受特征
本文采用体感温度作为人体感受特征,体感温度实际上是人通过皮肤与外界接触时在身体上或精神上所获得的一种感受。1984年,罗伯特·史特德(Robert G. Steadman)发表《体感温度的通用公式》(A universal scale of apparent temperature)为:
AT=1.07T+0.2e-0.65V-2.7
(2)
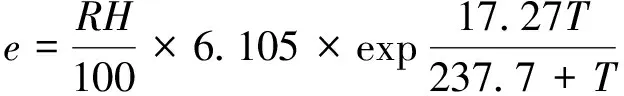
(3)
式中:AT为体感温度,℃;T为气温,℃;e为水汽压,hpa;V为风速,m/s;RH为相对湿度,%。此公式则由中央气象局预报各地体感温度所引用,本文同样引用该公式构造 “体感温度”特征。
6) 用户喜好特征
通过数据分析可看出,人们在相同外界环境的条件下对温度的喜好程度不同,因此本文将用户喜好大致分为3类:偏好热、偏好冷、中性。
ASHRAE55-92标准通过对人对周围环境的主观感觉的研究,确定了人体舒适环境参数的最佳范围及允许范围[8]。国内外学者在热舒适性方面做了大量现场及实验室研究,从而得到了人体关于空气温度或有效温度的热感觉方程,并给出了热舒适性的评价指标[9]。
本文采用的热舒适评价为PMV-PPD指标,PMV指标是引入反映人体热平衡偏离程度的人体热负荷TL而得出的。PMV指标采用了7级分度分别为热(+3)、暖(+2)、微暖(+1)、适中(0)、微凉(-1)、凉(-2)、冷(-3),具体PMV模型见图7[10]。

图7 PMV模型
Fanger认为[11-12],人在一定劳动强度条件下的冷热感觉只与人体热负荷有关。
具体PMV计算公式为
VPMV=(0.303e-0.036M+0.028)×L
L={(M-W)-3.15×10-3[5 733-6.99(M-W)-Pa]-
0.42[(M-W)-58.5]-
1.7×10-5M(5 857-Pa)-1.4×10-3M(34-ta)-
DPDD=100-95e-(0.033 58PMV4+0.217 9PMV2)
(4)
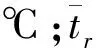
服装表面平均温度计算公式为
tcl=35.7-0.028(M-W)-
Rcl{39.6×10-9fcl[(tcl+273)4-(tr+273)4]+
fclhc(tcl-ta)}
(5)
对流换热系数与服装面积系数分别为:

(6)

(7)
为了求解PMV,需要对七项参数进行设定。求解过程和参数设置参考美国加州大学伯克利分校建筑环境中心CBE热舒适计算方法[8]。4项环境参数如下:
(1) 空气温度
它是影响热舒适的主要因素。本文计算中采用车内温度作为计算指标。
(2) 空气相对湿度
直接影响皮肤表面蒸发散热量,进而影响人体的舒适感。本文数据中缺少车内湿度数据,故以天气情况的相对湿度作为计算指标。
(3) 室内空气流动速度
影响人体的对流换热和蒸发换热。由于本文数据中缺少空调设定风速,故以默认风速0.1 m/s作为计算指标。
(4) 平均辐射温度
平均辐射温度大约等于车内当前的空气温度。因此在本文中平均辐射温度取为车内温度。
两项人体参数如下:
(1) 人体新陈代谢率
人体新陈代谢率在不同状态下有着较大差异,这取决于人的活动水平和环境条件。在CBE热舒适计算方法中规定了开轿车时的新陈代谢为1.5 met,等价于87.225 W/m2。
(2) 服装热阻
本文在计算服装热阻时借鉴韩滔[13]总结出的一个具体室外温度与对应衣服热阻的关系表,使得计算结果更准确。
7) 时间序列特征
时间序列预测方法有很多,本文通过构造时间序列特征将时间序列问题转换为机器学习的监督学习问题,并最终选择Lasso多元线性回归模型。
3.2 特征转换与数据划分
考虑到需要对比多种模型和集成处理的效果,对经过清洗的数据,离散型特征进行独热编码,连续型变量进行归一化处理。
为了保持每段行程完整和时间维度分配均匀,自定义了一种以日期为标准4∶1的比例划分方法来切分训练集和测试集。这样在划分数据时就可以保证一天内所有行程的数据保持完整。
3.3 特征筛选
特征筛选可以减少特征数量,使模型泛化能力更强,减少过拟合,增强对特征和特征值之间的理解,特征筛选的方法主要包括Filter方法、Wrapper方法和Embedded方法。本文通过数据清洗和特征工程,得到了20个维度的特征如表2所示。
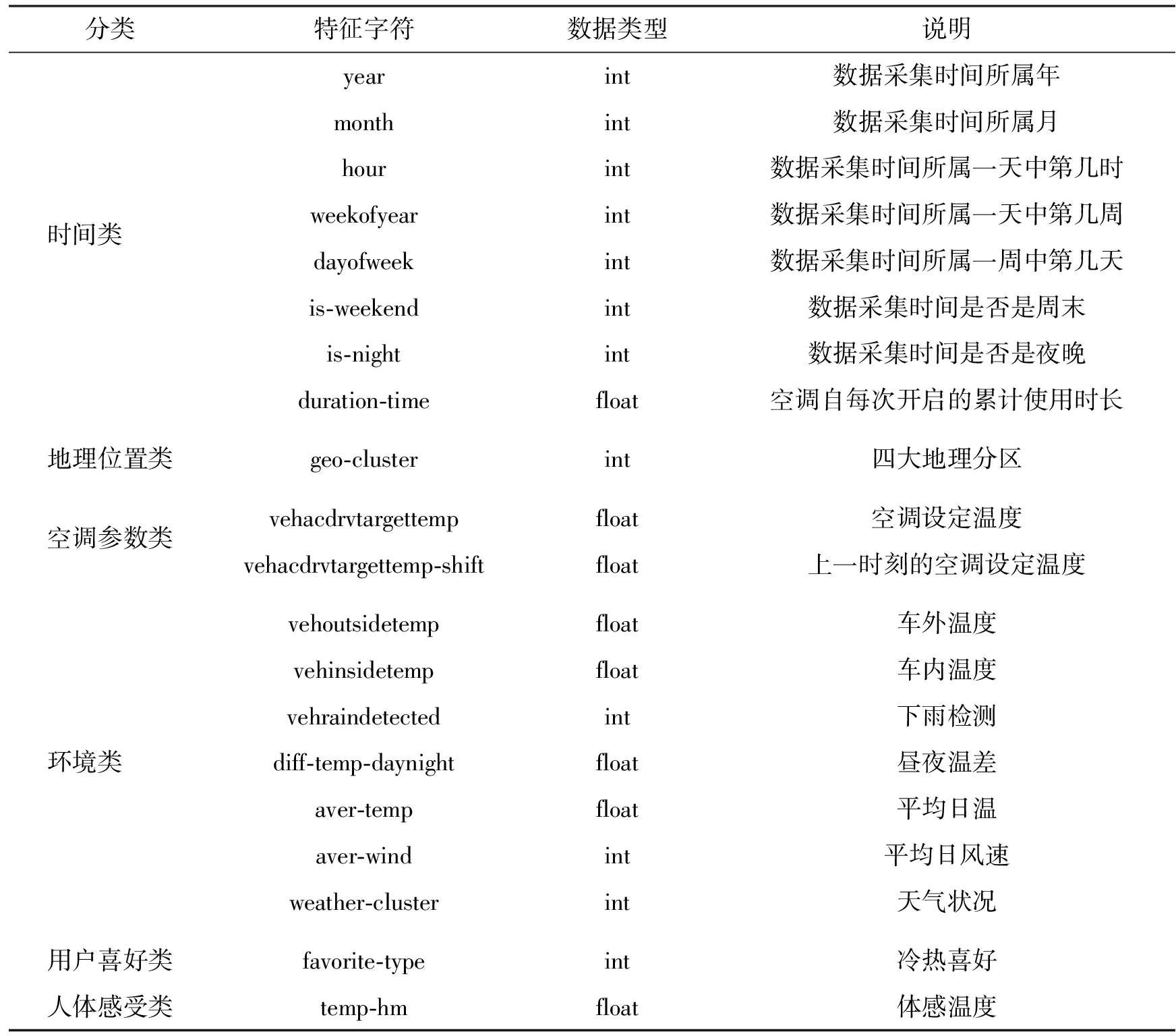
表2 数据预处理后的数据特征说明
本文中特征筛选是基于Filter方法中的皮尔逊相关系数法和基于随机森林的特征筛选方法来判断特征重要性从而删除无关冗余特征,方法流程图如图8所示。

图8 特征筛选方法流程图
其中皮尔逊相关系数计算公式为
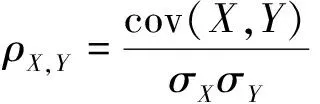
(8)
式中:cov(X,Y)为变量X,Y的协方差;σX和σY分别为X,Y的标准差;相关性系数ρX,Y的取值区间为[-1,1],-1表示完全的负相关,+1表示完全的正相关。
对表2中全部特征使用皮尔逊相关系数分析,得到相关系数热力图如图9所示。
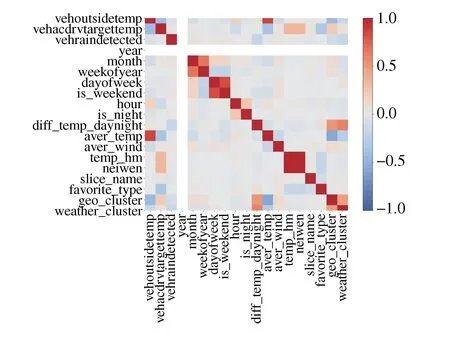
图9 皮尔逊相关系数热力图
Filter方法中的皮尔森相关系数法是一种分析变量特征和目标特征之间关系的方法,该方法主要用于分析特征之间的线性相关度,但不易于发现特征与特征之间的非线性相关关系,对于该问题可以引入基于树模型的方法。因为树模型的方法对非线性关系的特征处理简单快速,并且不需要太多的调试,但考虑到单颗决策树模型容易过拟合,所以本文利用基于随机森林的特征排序法来评价每个特征的重要性,删除无关冗余特征,进而优化模型结构。其中时间序列特征中的duration-time和vehacdrvtargettemp-shift用于训练时间序列温度预测模型,不用于训练习惯温度预测模型,因此共有17个特征进行筛选,最终得到结果如图10所示。

图10 随机森林特征筛选重要性结果
根据特征筛选结果,保留前10个最重要的特征,其中时间类特征包括6(hour)、8(dayofweek),地理位置类是10(geo-cluster),环境类包括3(vehoutsidetemp)、1(vehinsidetemp)、7(diff-temp-daynight)、5(aver-temp)和9(weather-cluster),用户喜好类是4(favorite-type),而人体感受特征是2(temp-hm),前10个特征的重要性占比之和高达97.4%,最后加上时间序列特征duration-time、vehacdrvtargettemp-shift和目标特征vehacdrvtargettemp从而构成最终的特征。其中人体感受特征中的体感温度与环境温度不同,其更能直接反映人体的热感受情况,当相对湿度越小、风速越大时,能得出较低的体感温度,而用户喜好类特征中的冷热喜好则是用户对于空调设定温度高低的喜好。
4 模型筛选与数据实验
4.1 模型筛选
在本文中,采用数据切分后的训练集来对习惯温度预测模型和时间序列温度预测模型进行筛选并使用交叉验证来对比模型的准确度和运算时间,其中需要交叉验证的模型为Ridge、ElasticNet、Lasso、AdaBoostRegressor、CART、Bagging、Random Forest Regressor、XGBRegressor、Gradient Boosting和LGBMRegressor。K折交叉验证(K Fold Cross Validation)[14]是将所有数据集分成K份,每次不重复地取其中一份做测试集,用其他K-1份做训练集训练模型,每次训练和预测都计算该模型在测试集上的MAPE,最后将K次的MAPE取平均得到最终的MAPE,即
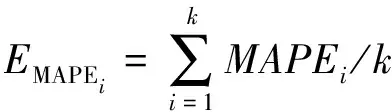
(9)
本文对训练样本的切分依旧采用以日期为标准4:1的比例进行切分。数据切分好之后开始迭代训练和验证,将每次验证的结果记做EMAPEi,最终模型的评价结果取5次MAPE的均值。
1) 习惯温度预测模型
习惯温度预测模型输出用户上车开启空调后一段时间内的空调设定温度,训练模型特征不包括时间记忆特征,其交叉验证结果如图11所示。

图11 习惯温度预测模型交叉验证结果
根据交叉验证结果,综合考虑模型精度与计算时间,本文习惯温度预测模型选择RF。RF算法是Bagging算法的代表,由于其良好的性能表现,被广泛应用到诸如领域。单棵决策树通常具有高方差,容易过拟合,而RF构建过程的Bagging思想能够降低方差,此外,RF在Bagging随机采样的思想上还增加了随机特征选择,使得其在训练过程中增加更多的随机性。
2) 时间序列温度预测模型
时间序列温度预测输出的是上车开启空调一段时间后实时的空调设定温度,时间序列模型是在基础特征的基础上加上了时间序列特征,其交叉验证结果如图12所示。
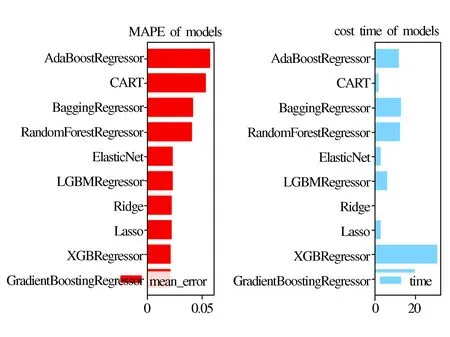
图12 时间序列温度预测模型交叉验证结果
根据交叉验证结果,综合考虑模型精度与计算时间,并且Lasso较为简单,可以减少计算资源,适合连续性的实时工作,因此本文时间序列温度预测模型选择Lasso。
4.2 调参优化与模型集成
在确定模型后,我们需要确定模型的超参数来提高模型的精度,常见的超参数寻优方法有网格搜索法和贝叶斯优化方法。考虑到Lasso回归模型简单、超参数少,所以对Lasso模型使用网格搜索法。而贝叶斯优化方法则充分利用了被测试点忽略的前一个点的信息,在该问题中贝叶斯优化方法是一种非常有效的优化算法[15-16],因此本文RF模型采用贝叶斯优化算法。
在模型筛选阶段,Lasso使用的Sklearn中的LassoCV,其中已加入网格搜索法自动寻优,最终得到惩罚系数alpha=0.007 512 482 411 700 719,优化后MAPE评分为0.0228。而RF模型通过贝叶斯优化后的MAPE评分从0.057 0降为了0.046 4。
最后根据本文提出的空调设定温度预测方法,将优化后的RF模型和Lasso模型进行集成,得到RF-Lasso集成模型,实现对用户期望的空调设定温度预测。RF-Lasso集成模型原理图如图13所示,X为时间序列输入,Y为模型输出,从集成方式上可以解释为RF与Lasso求解过程的集成。
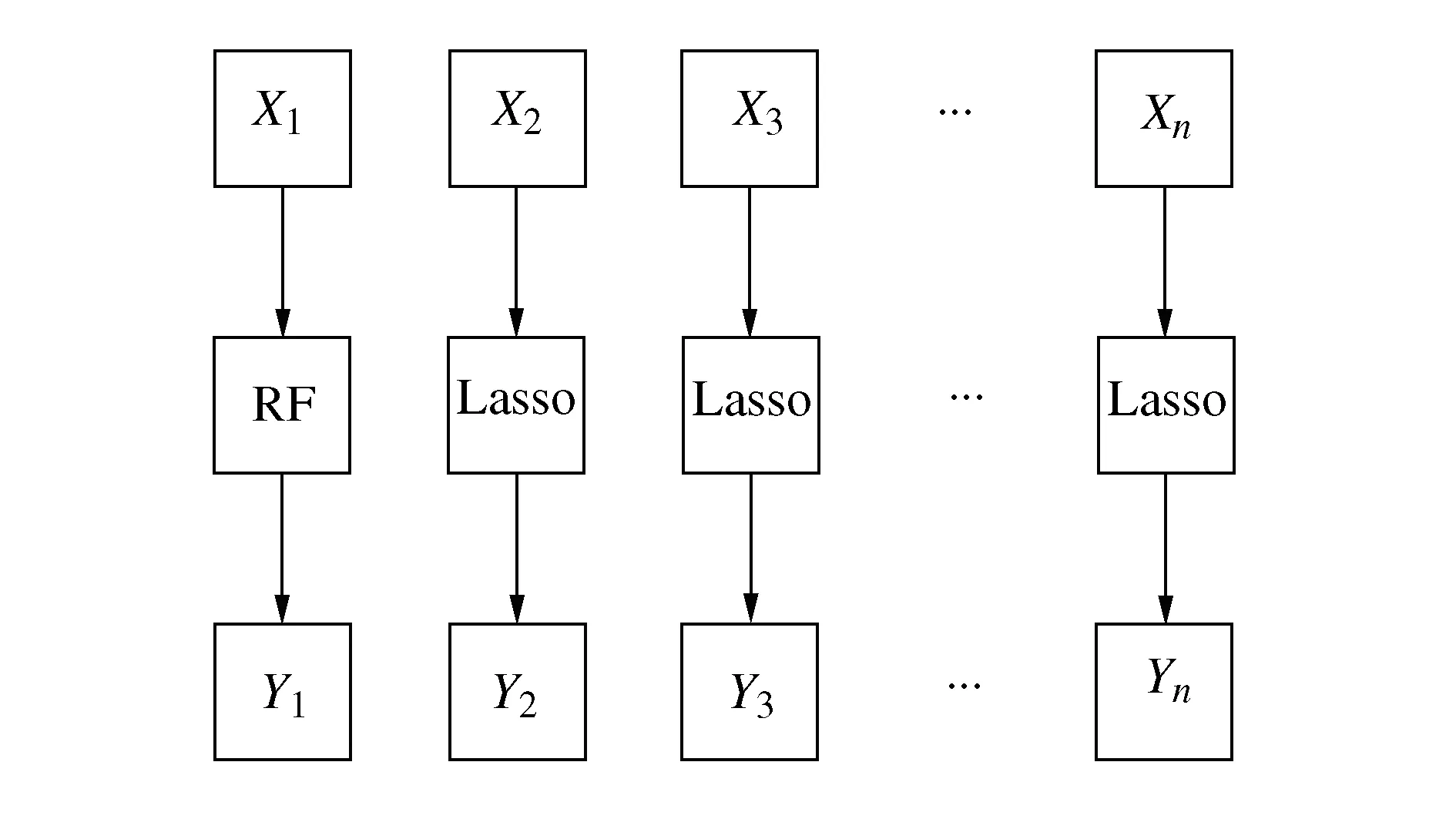
图13 RF-Lasso集成模型原理图
Xi作为RF-Lasso集成模型的输入,随着时间和模型的变化,其包含的特征也在变化,即
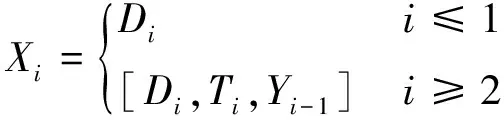
(10)
式中:Di为RF模型的输入特征;Ti为空调开启后的累计时间特征;Yi-1是上一时刻集成模型的输出结果,又作为Lasso模型i时刻的输入特征之一。
最终得到RF-Lasso集成模型为
(11)
4.3 数据试验
为了验证本次预测模型的准确性和可靠性,采用图14方法来完成数据试验。
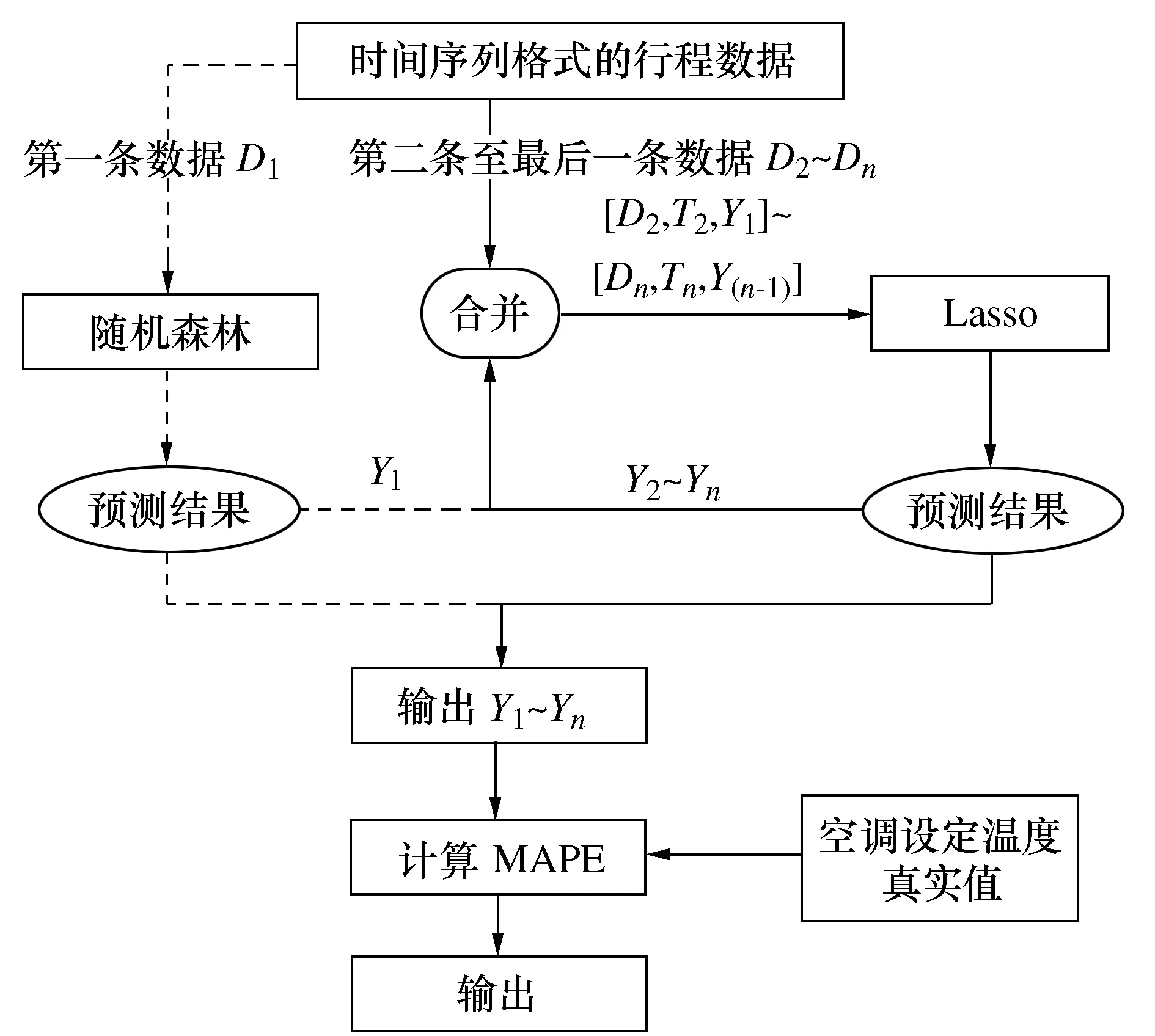
图14 RF-Lasso集成模型试验流程图
如图15所示,首先根据前文中找到的超参数对训练集S进行重新训练,以获得最佳模型。最后使用测试集T以验证模型的有效性,试验同样采用MAPE作为评价指标。
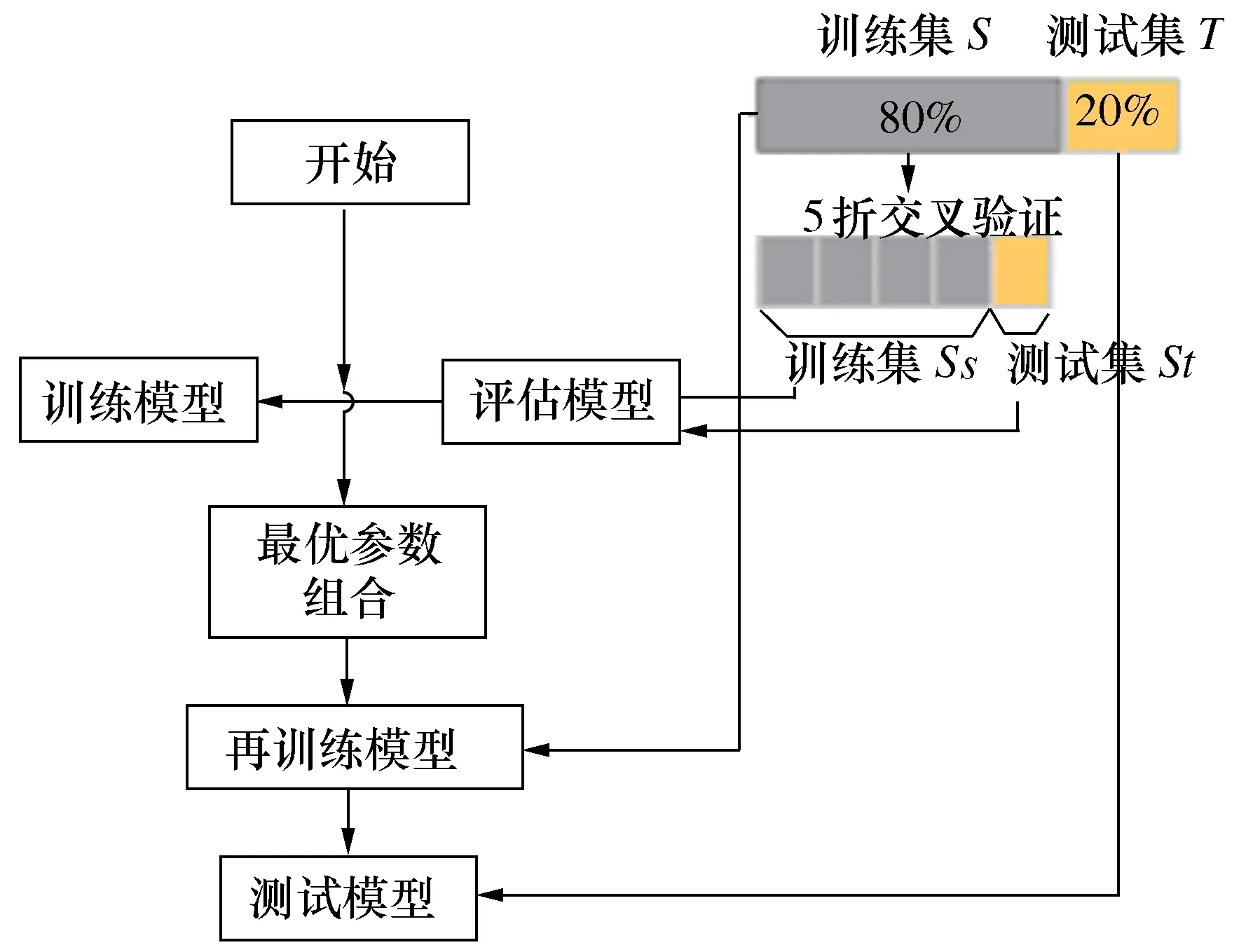
图15 数据试验流程图
首先对习惯温度预测模型RF和时间序列温度预测模型Lasso进行单模型测试,但是时间序列模型在固定步长下的表现不能代表模型实际情况下的效果,所以需要通过RF-Lasso集成模型来说明实际情况下的模型准确性。
在对集成模型进行数据试验时,按行程分段读入数据,每段行程第一条数据处理之后分配给RF模型,剩余数据处理之后分配给Lasso模型,集成模型具体数据试验如图14所示。
通过数据试验得到性能评价指标如表3所示。

表3 性能评价指标
从表3中可以看出习惯温度预测模型RF和时间序列温度预测模型Lasso在测试集上的MAPE得分与验证集上表现相似,证明模型都没有出现过拟合。而RF-Lasso集成模型的实验结果则与习惯温度预测模型效果相似,因此可以说明习惯温度预测模型的效果决定着集成模型的最终结果。
5 结论
本文以用户期望的空调设定温度预测为目标,基于车联网平台采集和存储的用户历史数据,利用数据挖掘和机器学习算法,构建了RF-Lasso集成预测模型。其中,通过数据清洗、有关特征构建和特征筛选,分析了与空调设定温度相关的影响因素,随后对比了10种机器学习回归算法,综合算法的精度和运算时间筛选出最适合本文的机器学习模型并利用网格寻优和贝叶斯优化算法优化模型参数,从而得到优化RF和Lasso模型,最后根据本文提出的空调设定温度预测方法,集成得到RF-Lasso模型。结果表明,本文提出的空调设定温度预测模型对用户空调设定温度预测结果的平均绝对百分比误差(MAPE)为0.049,预测结果较为理想,说明模型具有良好的准确性和鲁棒性。

