考虑齿厚偏差的圆柱齿轮副振动特性分析
李孟飞,胡玉梅,沈龙江,戴兴梦,余媛媛
(重庆大学 汽车工程学院,重庆 400044)
齿轮传动作为各类机械中最常用的传动之一,具有工作可靠、传动比准确和动力损失少等优点[1-3]。但由于制造、安装误差的存在,齿轮将存在各种偏差。偏差的存在会改变齿轮的啮合位置,使得实际啮合位置与理论啮合位置不重合,从而产生附加位移激励,是引起齿轮传动装置振动的重要原因[4]。常乐浩等[5]通过建立齿轮动力学模型,分析了多种齿廓偏差对直齿轮啮合副振动响应的影响规律。王奇斌与张义民[6]运用数值仿真方法研究了齿距偏差对齿轮转子系统振动特性的影响。周洋与李积鹏[7]采用理论公式计算和有限元仿真相结合的方法,研究了中心距偏差对具有梯度结构圆弧齿轮齿面接触应力的影响规律。肖鹏程[8]综合数值仿真和有限元仿真方法,研究了轴线偏差对斜齿轮工作齿面磨损的影响。
齿厚偏差作为齿轮偏差的一种,对齿轮的实际啮合状态有着重要影响。一方面,齿厚偏差直接影响到齿轮的啮合齿廓,从而影响齿轮时变啮合刚度,而齿轮时变啮合刚度是齿轮传动系统最重要的内部激励之一[9-10];另一方面,齿轮副侧隙通常是通过控制齿轮的齿厚偏差实现的[11],那么齿厚偏差的变化必然会影响到齿轮的侧隙大小,而侧隙大小直接决定了齿轮是否会产生齿间冲击,从而加剧齿轮传动系统的振动和噪声[12]。因此,研究齿厚偏差对齿轮啮合副振动特性的影响规律,对齿轮传动系统减振降噪设计有着重要的意义。而通过总结已有的研究工作可知,较少见到对仅含齿厚偏差这一单项偏差的齿轮进行动力学分析的研究工作,而对仅含齿厚偏差的圆柱齿轮进行动力学分析的研究工作几乎没有。
本文基于齿轮设计分析软件KISSsoft,建立了含不同齿厚偏差的圆柱齿轮副啮合刚度和传递误差计算模型,计算了含齿厚偏差圆柱齿轮副的啮合刚度和传递误差,并结合有限元仿真方法研究了齿厚偏差对圆柱齿轮副振动特性的影响规律,最后分析了不同齿厚偏差量、不同螺旋角和不同作用扭矩下圆柱齿轮副的振动特性,为进一步提出齿轮偏差控制原则奠定了理论基础。
1 模型建立
由于齿轮副侧隙通常是通过控制齿厚偏差实现的,所以实际运行中的齿轮必然存在一定的齿厚偏差,而制造和安装误差以及温度变化又会进一步影响齿厚偏差[13]。本节首先建立了考虑齿厚偏差的圆柱齿轮副啮合刚度和传递误差激励计算模型,然后建立了考虑齿厚偏差的圆柱齿轮啮合副有限元模型,为后续分析做铺垫。
1.1 啮合刚度和传递误差计算模型建立
圆柱齿轮齿厚是指任意圆周上一个轮齿两侧齿廓间的弧线长度,以si表示,对于斜齿轮,指法向齿厚,分度圆齿厚通常用s表示。而齿厚偏差是指齿轮分度圆柱面上齿厚的实际值与公称值的差值[14],以ΔEs表示。ΔEss表示上偏差, ΔEsi表示下偏差,T表示齿厚公差,如图1所示。
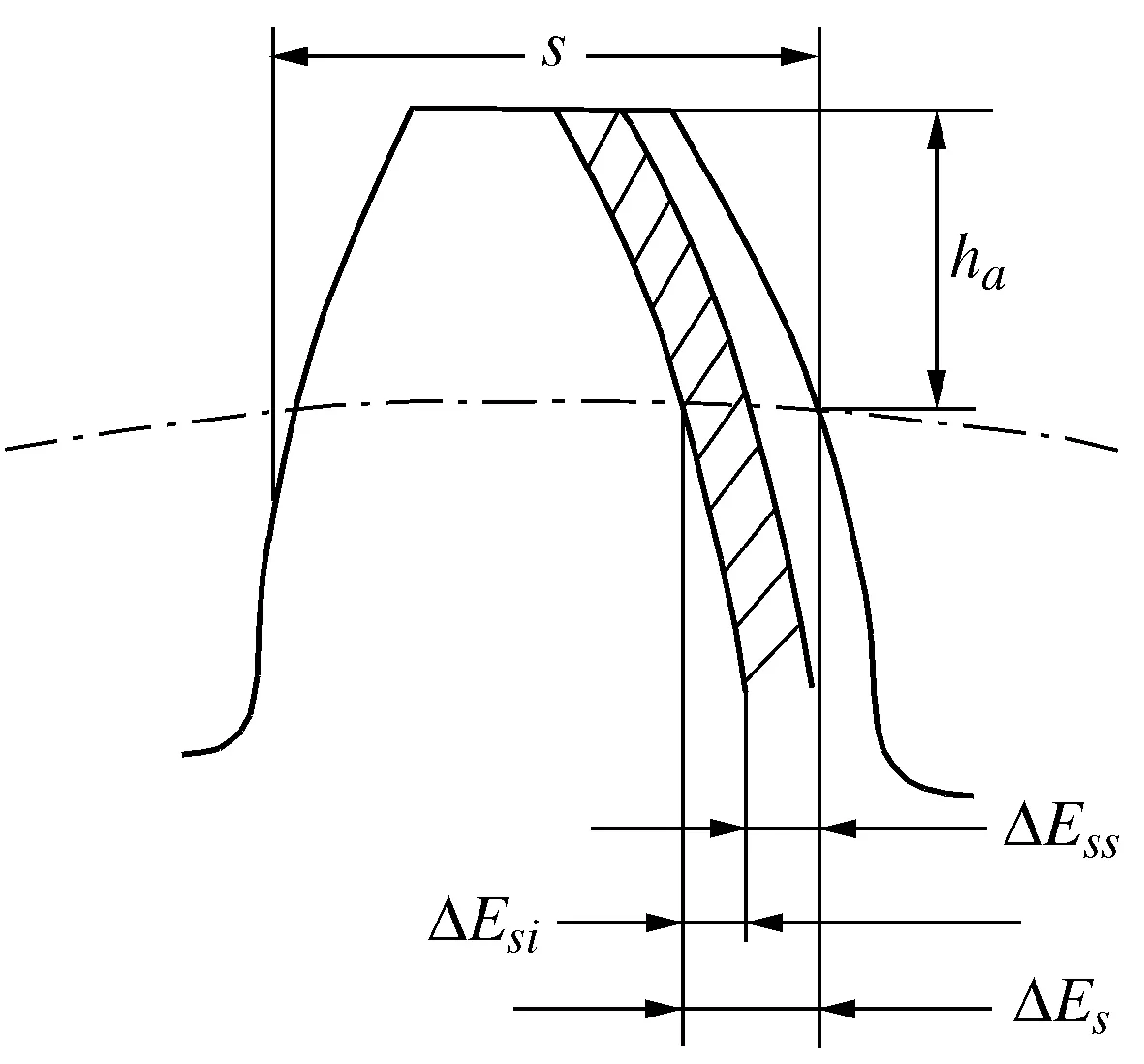
图1 齿厚偏差
由图1可以看到,渐开线圆柱齿轮的齿厚偏差是有大小、方向(周向、法向和弦向)和位置(固定弦、分度圆和中圆)的矢量。因此要确定齿厚偏差的大小,还要明确它的方位,且要区别它的定义方位和测量方位。如果测量方位失误,那末它的测量值也就失真。本文所指的齿厚偏差均为分度圆上的法向齿厚偏差。
为确保齿轮能够正常运转,不出现脱离啮合、卡死以及润滑不良等现象,在每一对啮合齿间必须留有合适的侧隙。为满足不同的侧隙要求,主要有基中心距制和基齿厚制两种方法。由于切齿中削薄齿厚较方便,因此标准大多采用基中心距制。在基中心距制中,齿厚就相当于基孔制中间隙配合的轴,所以齿厚上下偏差均为负值[15]。齿轮设计者通常会给出齿厚极限偏差代号,根据齿厚极限偏差代号查阅标准便可得到对应的齿厚偏差。
本文所用齿轮基本参数如表1所示。

表1 齿轮基本参数
根据齿厚极限偏差代号查得大小齿轮齿厚及上下偏差如表2所示。
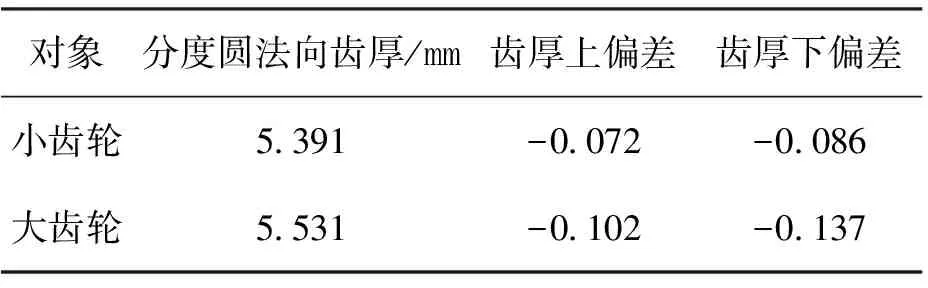
表2 齿厚及偏差
齿轮设计分析软件KISSsoft是根据输入的齿厚上下偏差所确定的范围来控制齿轮的实际齿厚偏差,很明显当齿厚上下偏差都取相同值时便可得到具有任一确定齿厚偏差的齿轮副。为研究不同齿厚偏差对齿轮副振动特性的影响规律,分别建立具有如表3所示齿厚偏差的齿轮副啮合模型,其中ΔEs0表示无齿厚偏差。
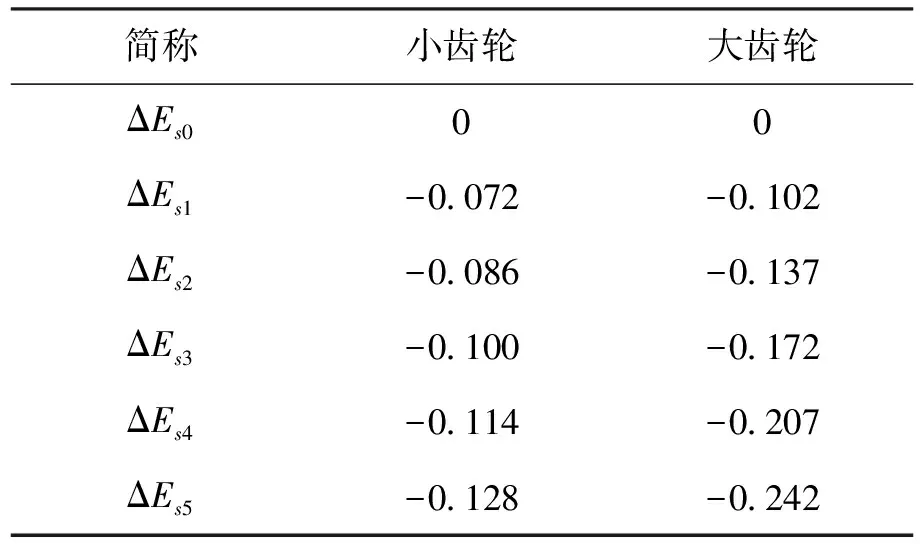
表3 本文所取齿厚偏差
使用KISSsoft按上述基本参数和齿厚偏差分别建立齿轮副啮合刚度激励和传递误差激励计算模型,同时建立含不同齿厚偏差的齿轮副三维模型,如图2所示。

图2 含齿厚偏差的齿轮啮合副三维模型
1.2 有限元模型建立
将在KISSsoft里建立的含不同齿厚偏差的齿轮副三维模型以IGES格式输出,在有限元前处理软件ANSA中进行有限元建模,得到含齿厚偏差的齿轮啮合副有限元模型如图3所示。

图3 含齿厚偏差的齿轮啮合副有限元模型
这里建立的有限元模型共有380 720个单元,589 128个节点。施加边界条件时,将齿轮的内孔表面视作刚性体,约束其5个自由度,仅保留绕轴向转动的自由度,小齿轮施加转速2 010 r/min,从动轮大齿轮施加扭矩1 812.5 Nm,采用面-面接触定义齿轮副接触,摩擦因数取0.1。最后将模型以K文件格式导入到LS-DYNA进行求解。
2 齿轮副振动特性分析
利用建立的含不同齿厚偏差的圆柱齿轮副激励计算模型和有限元模型,分别分析齿厚偏差对圆柱齿轮啮合刚度激励、传递误差激励和振动响应的影响。
2.1 齿厚偏差对齿轮副啮合刚度和传递误差影响分析
时变啮合刚度激励和传递误差激励是齿轮实际运转过程中非常重要的两个激励,会直接对齿轮啮合副的振动响应产生很大影响[16-18]。而齿厚偏差的存在又会直接对齿轮副的啮合刚度和传递误差产生影响,这是由于齿厚偏差改变了齿轮的工作齿廓,使得齿轮在啮合过程中的某些时刻参与啮合的轮齿对数发生了变化。因此,这里首先分析了齿厚偏差对齿轮副啮合刚度和传递误差的影响规律。
利用齿轮啮合刚度和传递误差激励计算模型,分别计算无齿厚偏差和齿厚偏差为ΔEs2时齿轮副的啮合刚度和传递误差。
两种偏差下齿轮副单齿啮合刚度曲线见图4。
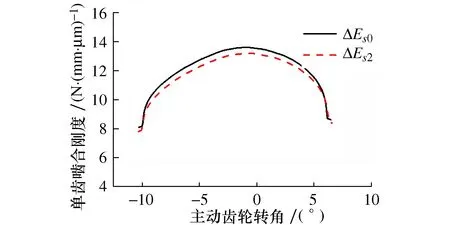
图4 单齿啮合刚度对比图
由图4可得,一个啮合周期中的单齿啮合刚度曲线大致呈现为两段抛物线,这是由于斜齿轮在进入和退出啮合的瞬时位置,啮合线位于齿面的上部,离约束位置更远,齿轮啮合副相对变形更大,啮合刚度更小。啮合线长度相同的位置,远离进入啮合和退出啮合的位置啮合刚度更大,因此一个啮合周期中的啮合刚度曲线大致呈现为两段抛物线,这与文献[19]所给出的结论一致。同时,齿厚偏差的存在,使得齿轮副单齿啮合刚度降低,这是由于齿厚偏差的存在导致齿轮轮齿厚度降低。
两种偏差下齿轮副传递误差如图5所示。
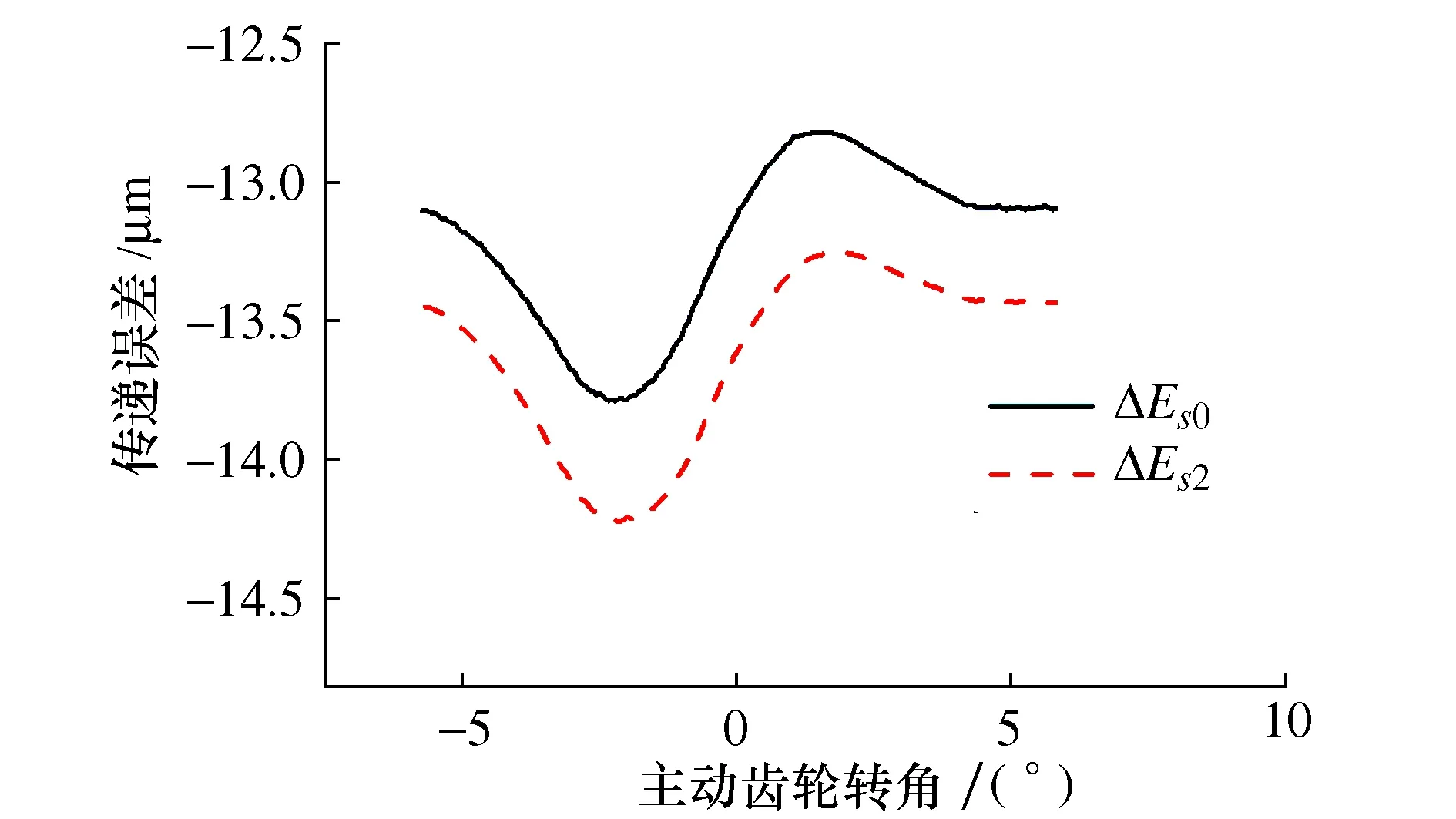
图5 传递误差对比
可以看到,一个啮合周期中,齿轮副传递误差随齿轮转角而改变,并且由于齿厚偏差的存在,齿轮副传递误差明显增大。作为齿轮传动系统最重要的内部激励之一,传递误差激励的增大将直接影响到齿轮副的振动特性。
2.2 齿厚偏差对齿轮副振动响应影响分析
借助ANSYS/LS-DYNA对齿轮啮合副有限元模型进行求解,得到齿轮应力云图如图6所示。
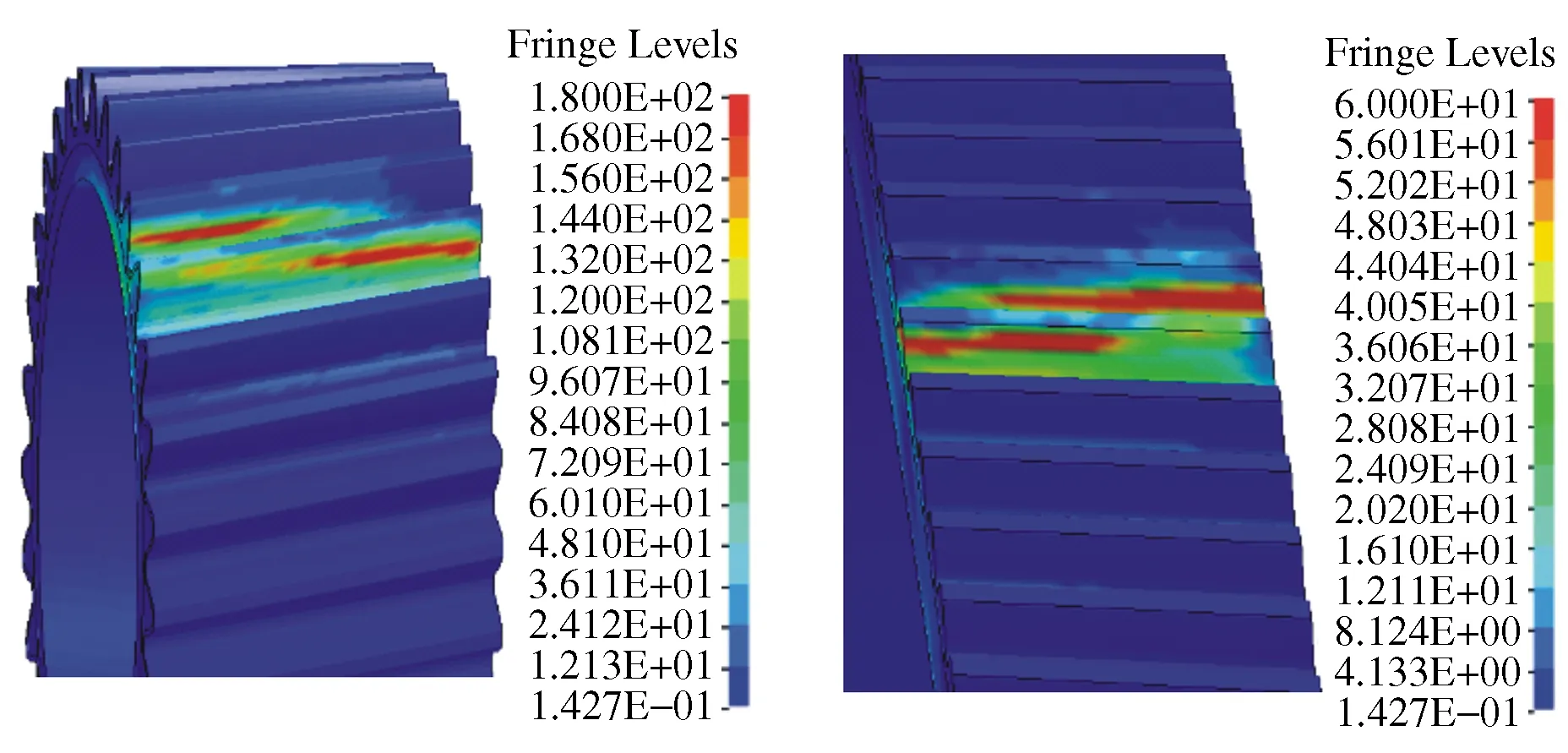
图6 齿轮应力云图
通过大小齿轮应力云图可以看出,齿面应力分布均匀,未出现偏载,齿轮啮合正常。提取两种偏差对应的大齿轮转速曲线如图7所示。
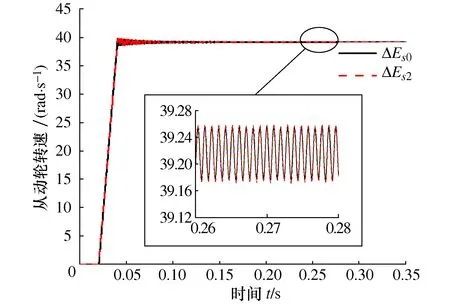
图7 大齿轮转速曲线
从大齿轮转速曲线可以用看出,加载稳定后大齿轮转速平稳,为39.22 rad/s,理论计算值为39.29 rad/s,误差仅为0.18%,说明仿真结果可靠。同时,无齿厚偏差和齿厚偏差为ΔEs2时转速曲线无太大差异,但齿厚偏差为ΔEs2时转速波动略大一些。
齿轮副动态啮合力是齿轮啮合系统的主要激励,其波动曲线能够直观地表明齿轮副啮合振动情况[20-21]。提取无齿厚偏差和偏差齿厚偏差为ΔEs2时齿轮副动态啮合力如图8所示。
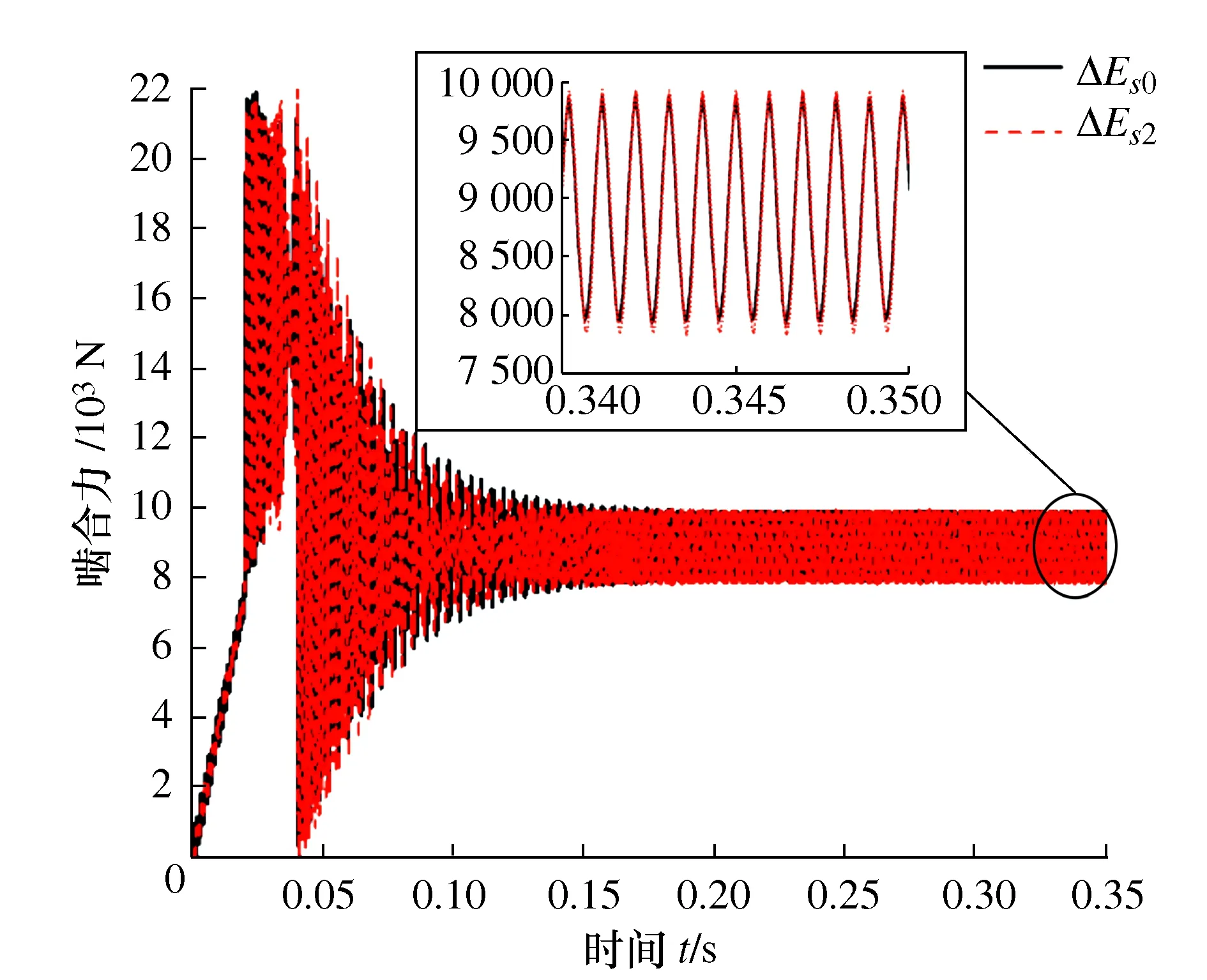
图8 啮合力对比图
从啮合力波动曲线可以看出,由于齿厚偏差的存在,齿轮副动态啮合力波动增大,齿轮啮合副振动增大。这并不难理解,齿厚偏差的存在已经使得传递误差激励明显增大,这必然导致齿轮副啮合振动增大。总之,由于齿厚偏差的存在,齿轮副单齿啮合刚度降低,传递误差增大,齿轮副振动更加剧烈。
3 参数影响
3.1 齿厚偏差量的影响
为了研究齿厚偏差量对齿轮副振动特性的影响,保持其他参数不变,分别采用ΔEs0~ΔEs5对应的齿厚偏差来分析齿轮副的两个激励和振动响应。
不同齿厚偏差量下齿轮副啮合刚度见图9。
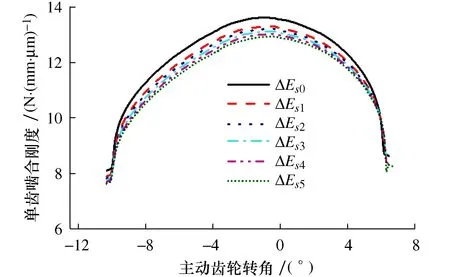
图9 不同齿厚偏差量单齿啮合刚度
由图9可得,随着齿厚偏差量增大,齿轮副单齿啮合刚度逐渐降低,这是由于齿厚偏差量的增大导致齿轮轮齿厚度不断减小。
不同齿厚偏差量下齿轮副传递误差如图10所示。
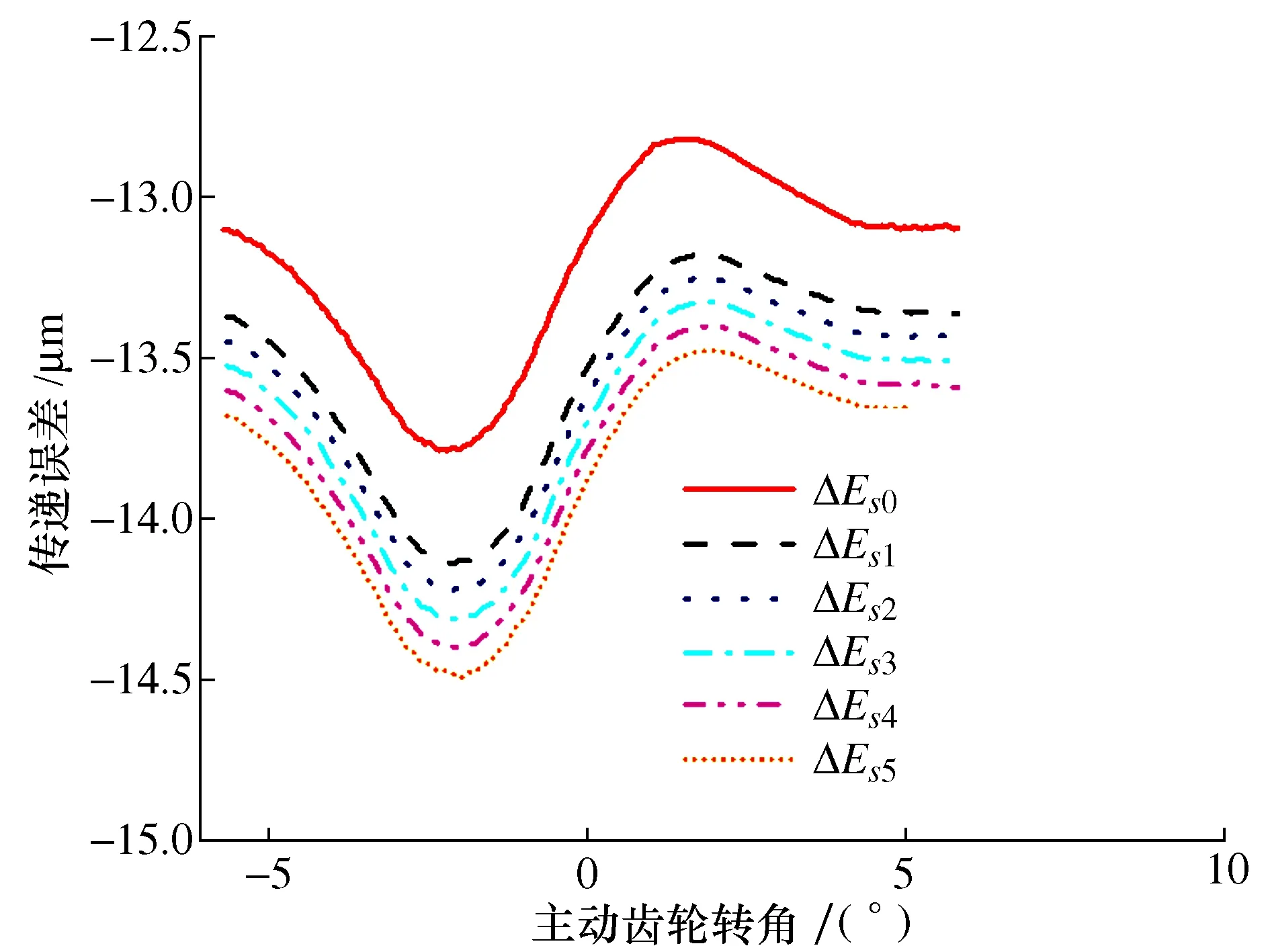
图10 不同齿厚偏差量传递误差
由图10可得,随着齿厚偏差量增大,齿轮副传递误差逐渐增大,传递误差激励的增大将会直接影响齿轮副振动特性。
不同齿厚偏差量下齿轮副动态啮合力波动大小如表4所示,其中齿厚偏差为ΔEs0和ΔEs5时动态啮合力分别如图11和图12所示。
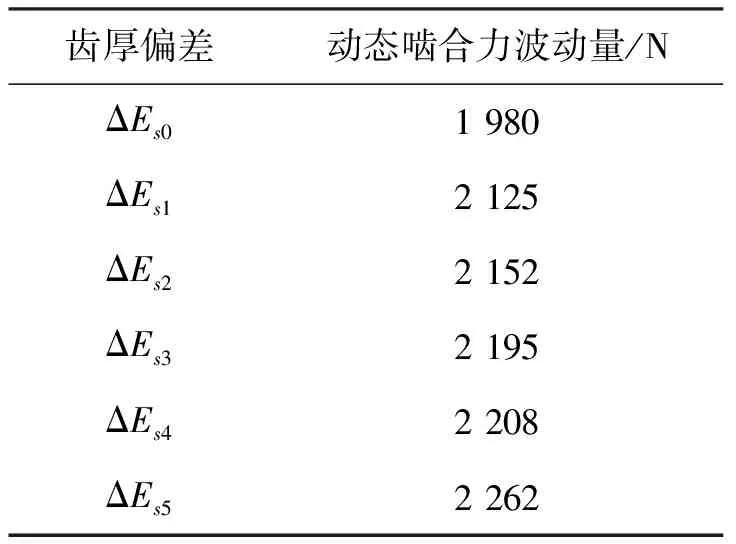
表4 不同齿厚偏差动态啮合力波动量
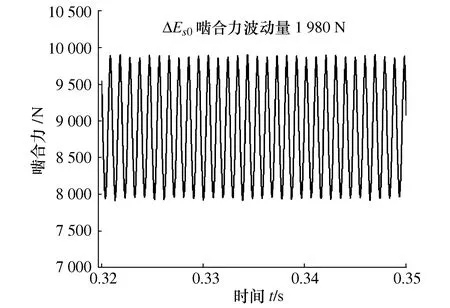
图11 齿厚偏差ΔEs0动态啮合力
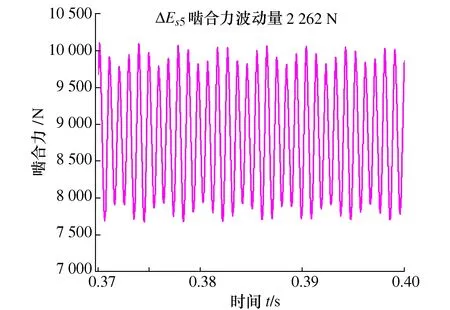
图12 齿厚偏差ΔEs5动态啮合力
可以发现,随着齿厚偏差增加,齿轮动态啮合力波动不断增大,这说明齿轮副振动增大。这是因为齿厚偏差增大导致齿轮副侧隙和传递误差激励增大,在二者共同作用下系统振动更加明显。
3.2 螺旋角的影响
为了研究不同螺旋角对齿轮副振动特性的影响,保持其他参数不变,分别分析螺旋角为0、10°和25°时齿轮副的激励和振动响应。不同螺旋角下齿轮副啮合刚度分别如图13~图15所示。
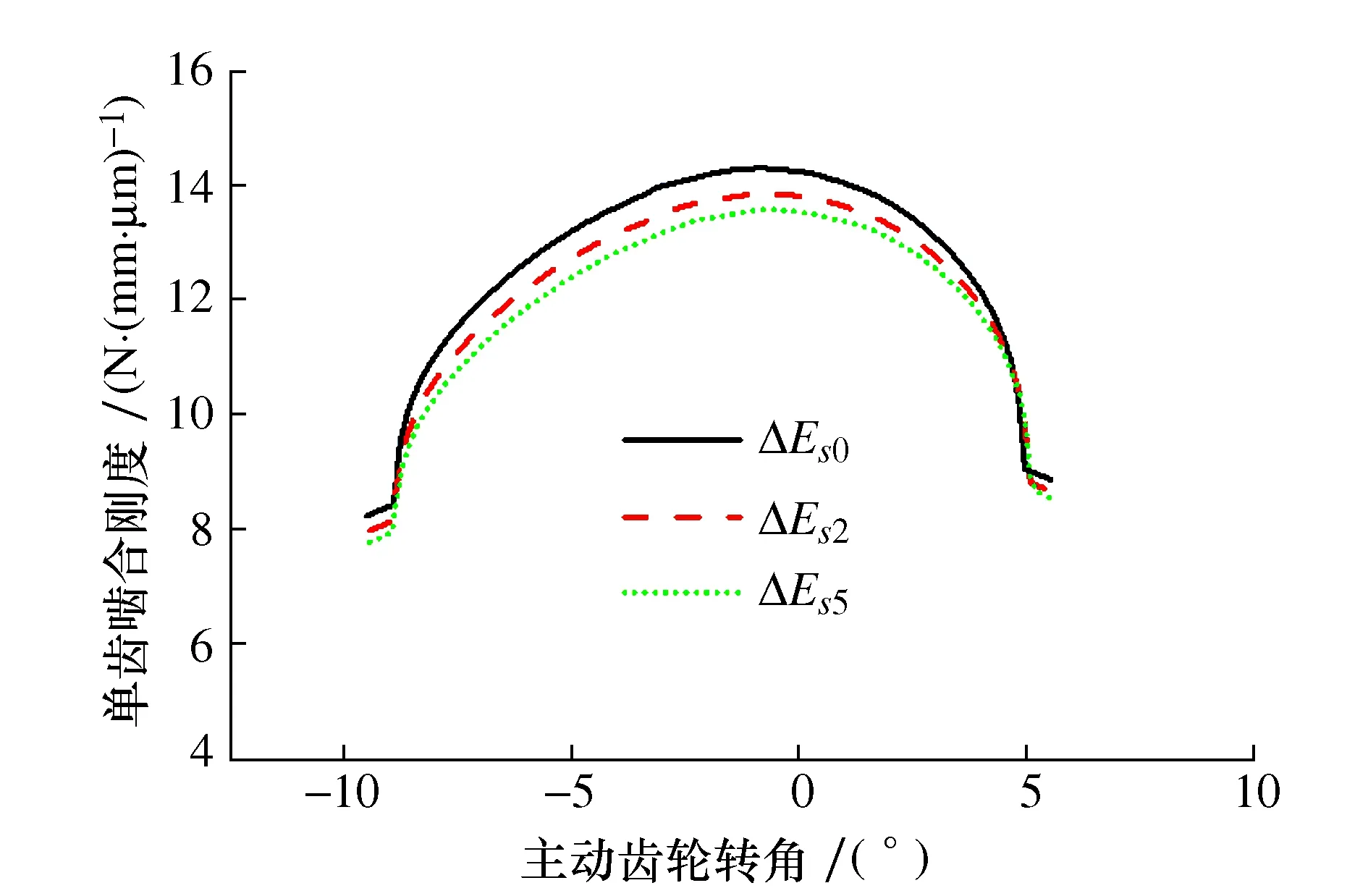
图13 β=25°啮合刚度
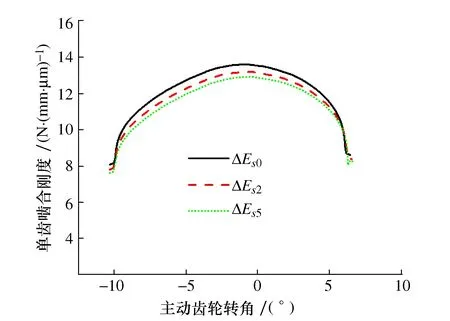
图14 β=10°啮合刚度
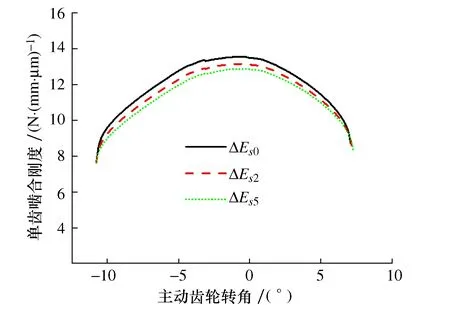
图15 β=0啮合刚度
由图13~图15可得,相同螺旋角下,随着齿厚偏差增大,齿轮副单齿啮合刚度降低,这与前面的结论是一致的;相同齿厚偏差下,随着螺旋角减小,齿轮副单齿啮合刚度降低。这是由于螺旋角减小导致齿轮副重合度降低,同时参与啮合的轮齿对数减少。
不同螺旋角下齿轮副传递误差分别如图16~图18所示。
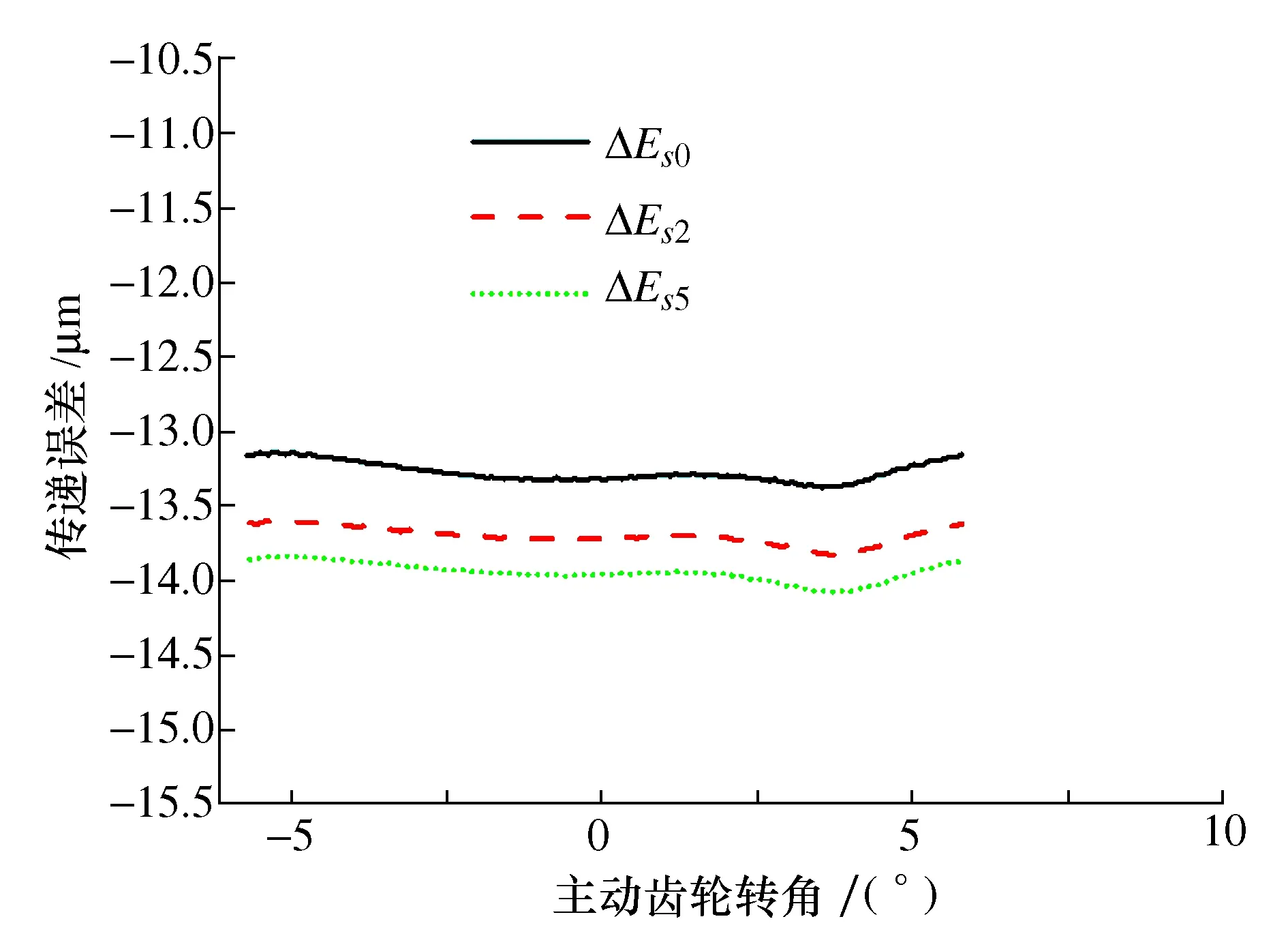
图16 β=25°传递误差
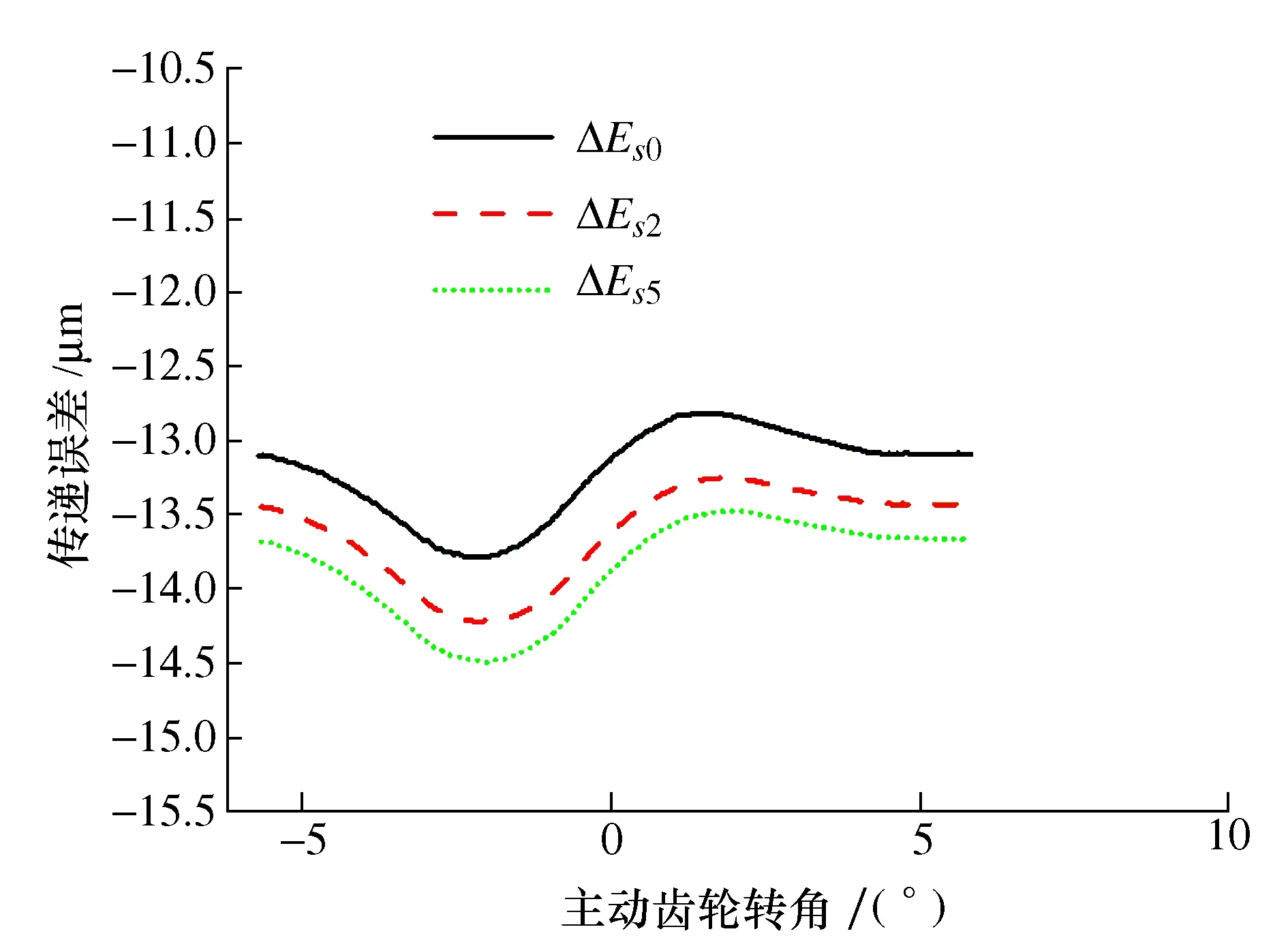
图17 β=10°传递误差
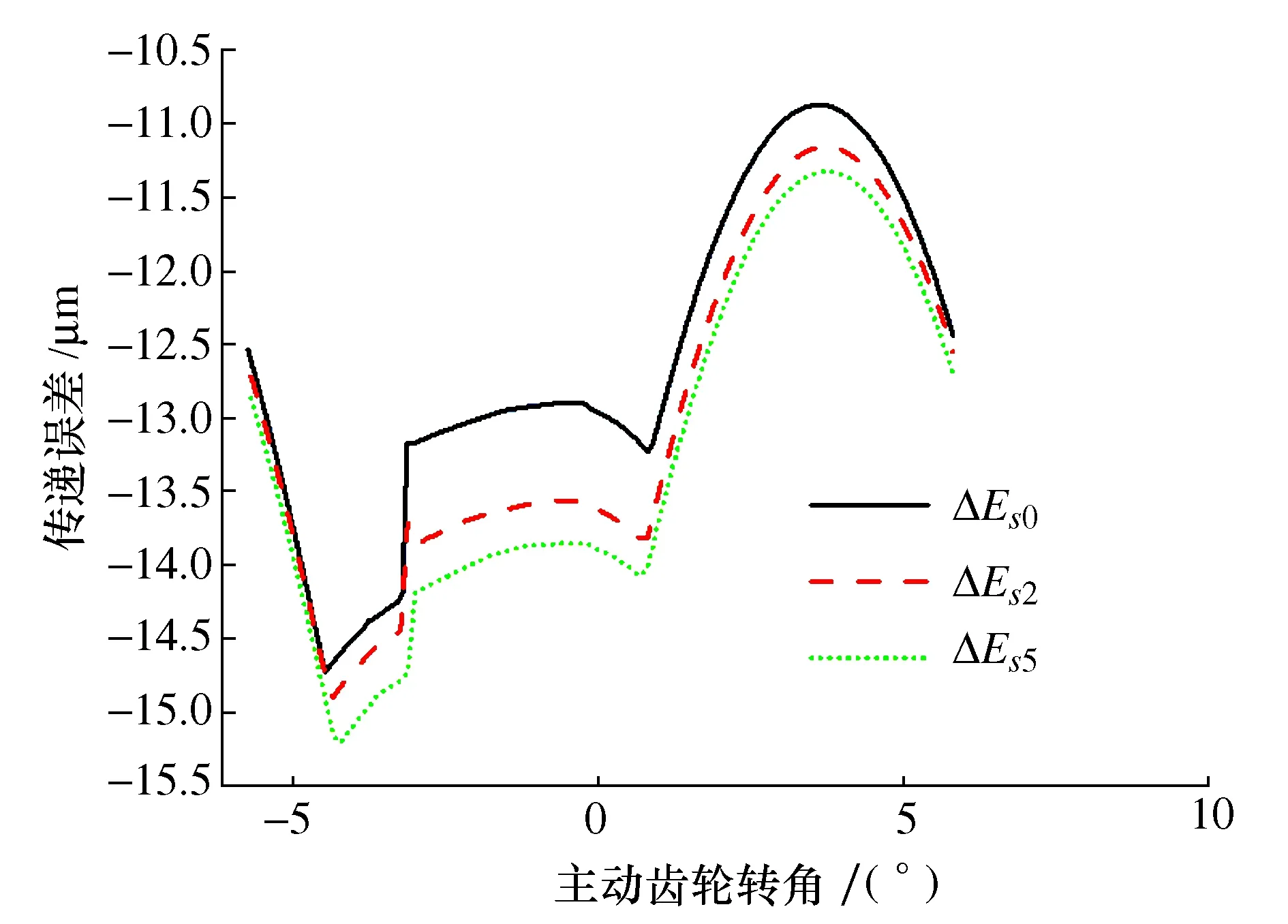
图18 β=0传递误差
由图16~图18可得,相同螺旋角下,随着齿厚偏差增大,齿轮副传递误差增大,这与前面的结论是一致的;螺旋角对齿轮副啮合状况影响显著,相同齿厚偏差下,随着螺旋角减小,传递误差激励波动量明显增大。
不同螺旋角下齿轮副动态啮合力分别如图19~图22所示。
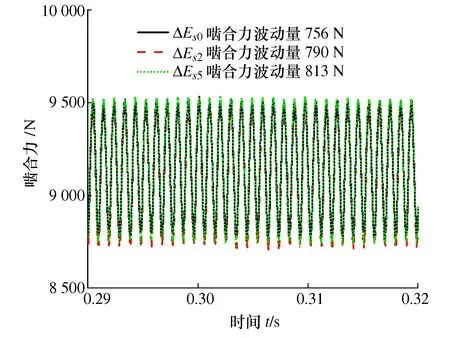
图19 β=25°动态啮合力
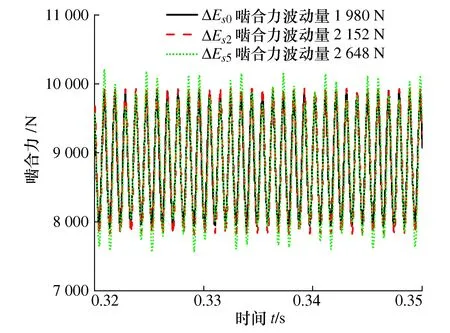
图20 β=10°动态啮合力
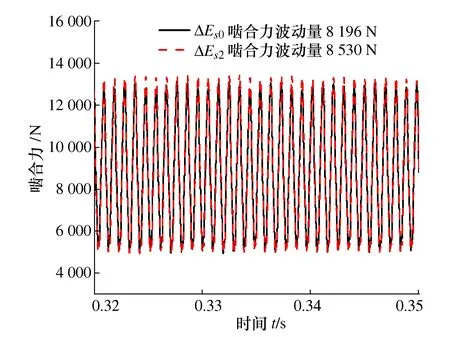
图21 β=0动态啮合力
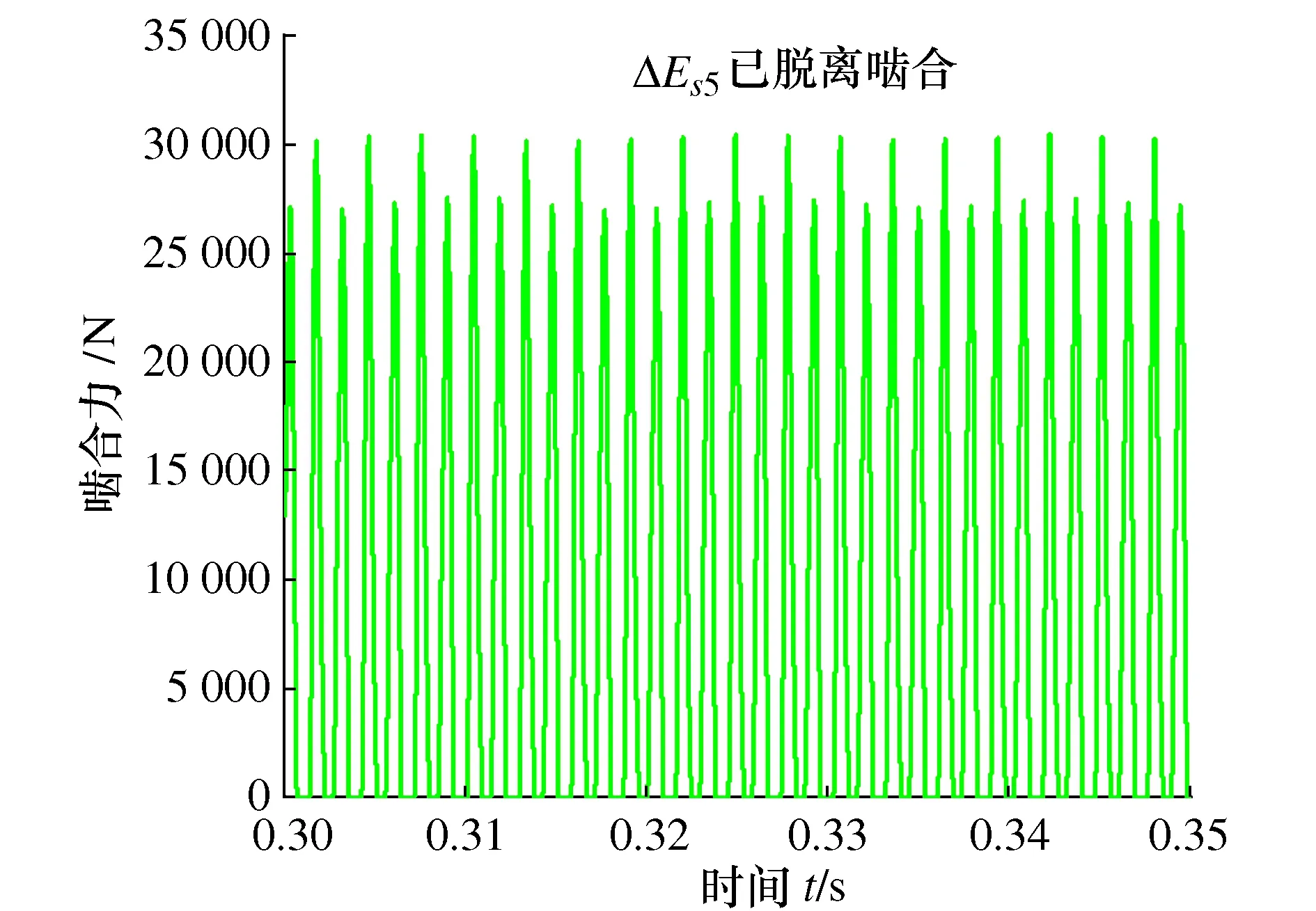
图22 β=0齿厚偏差ΔEs5时动态啮合力
由图19~图22可得,相同螺旋角下,随着齿厚偏差增大,动态啮合力波动增大,齿轮副振动增大,这与前面的结论是一致的;螺旋角对齿轮副啮合状况影响显著,相同齿厚偏差下,随着螺旋角减小,动态啮合力波动明显增大,齿轮副振动增大。同时可以看到,随着螺旋角减小,齿轮副振动特性对齿厚偏差更加敏感,当螺旋角为0时,齿厚偏差ΔEs5对应的齿轮副已经脱啮,无法正常啮合。
3.3 作用扭矩的影响
为了研究不同作用扭矩对齿轮副振动特性的影响,保持其他参数不变,分别分析作用扭矩为1 T、0.5 T和 0.25 T 时齿轮副的两个激励和振动响应。不同作用扭矩下齿轮副啮合刚度曲线如图23所示。
由图23可得,相同作用扭矩下,随着齿厚偏差增大,齿轮副单齿啮合刚度降低,这与前面的结论是一致的;相同齿厚偏差下,随着作用扭矩减小,齿轮副单齿啮合刚度降低。这种现象主要是由接触变形随载荷非线性变化所引起的,当作用扭矩较小时,齿轮副总啮合力也较小,两齿轮刚产生接触,此时更容易产生局部的接触变形,由接触变形引起的接触刚度较小,进而导致啮合刚度减小,这与文献[22]结论一致。
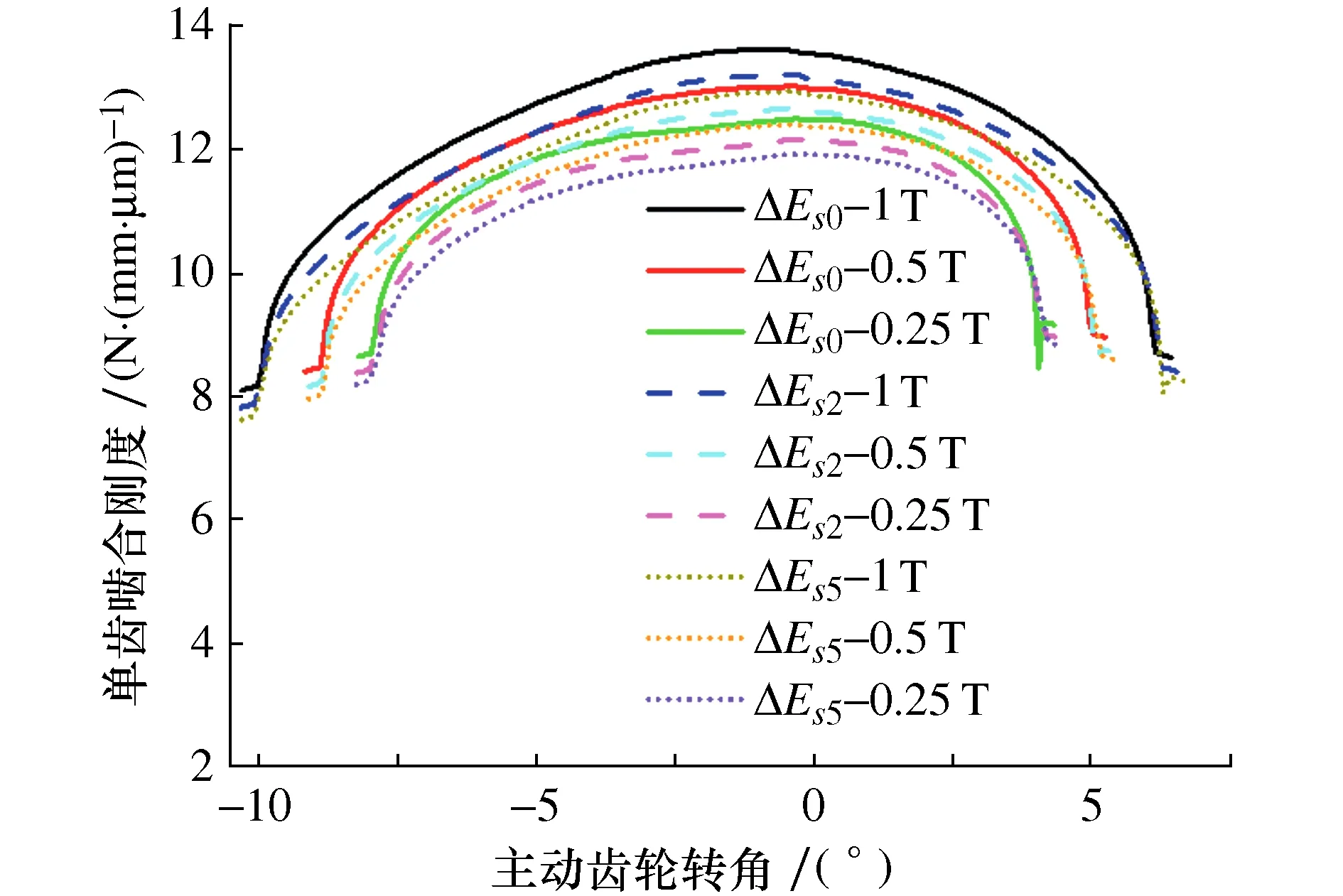
图23 不同作用扭矩下啮合刚度
不同作用扭矩下齿轮副传递误差如图24所示。
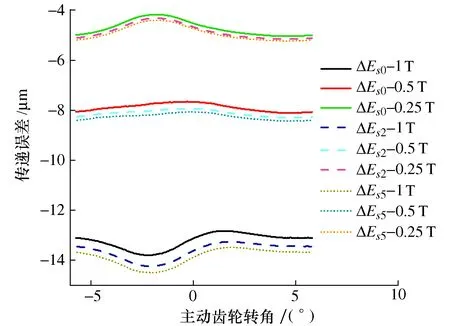
图24 不同作用扭矩下传递误差
由图24可得,相同作用扭矩下,随着齿厚偏差增大,齿轮副传递误差增大,这与前面的结论是一致的;相同齿厚偏差下,随着作用扭矩减小,传递误差明显减小。
不同作用扭矩下齿轮副动态啮合力分别如图25~图27所示。
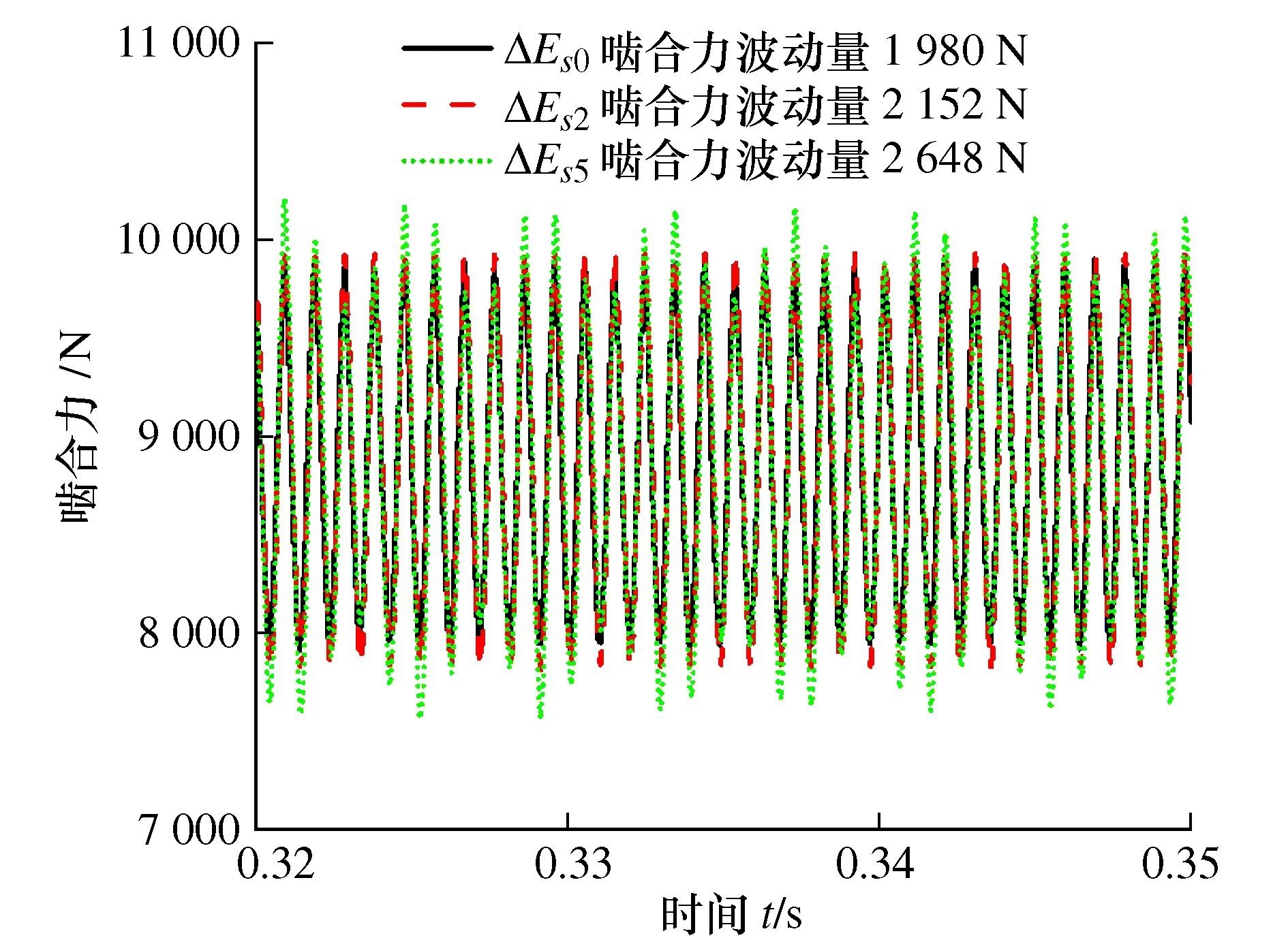
图25 作用扭矩1 T动态啮合力
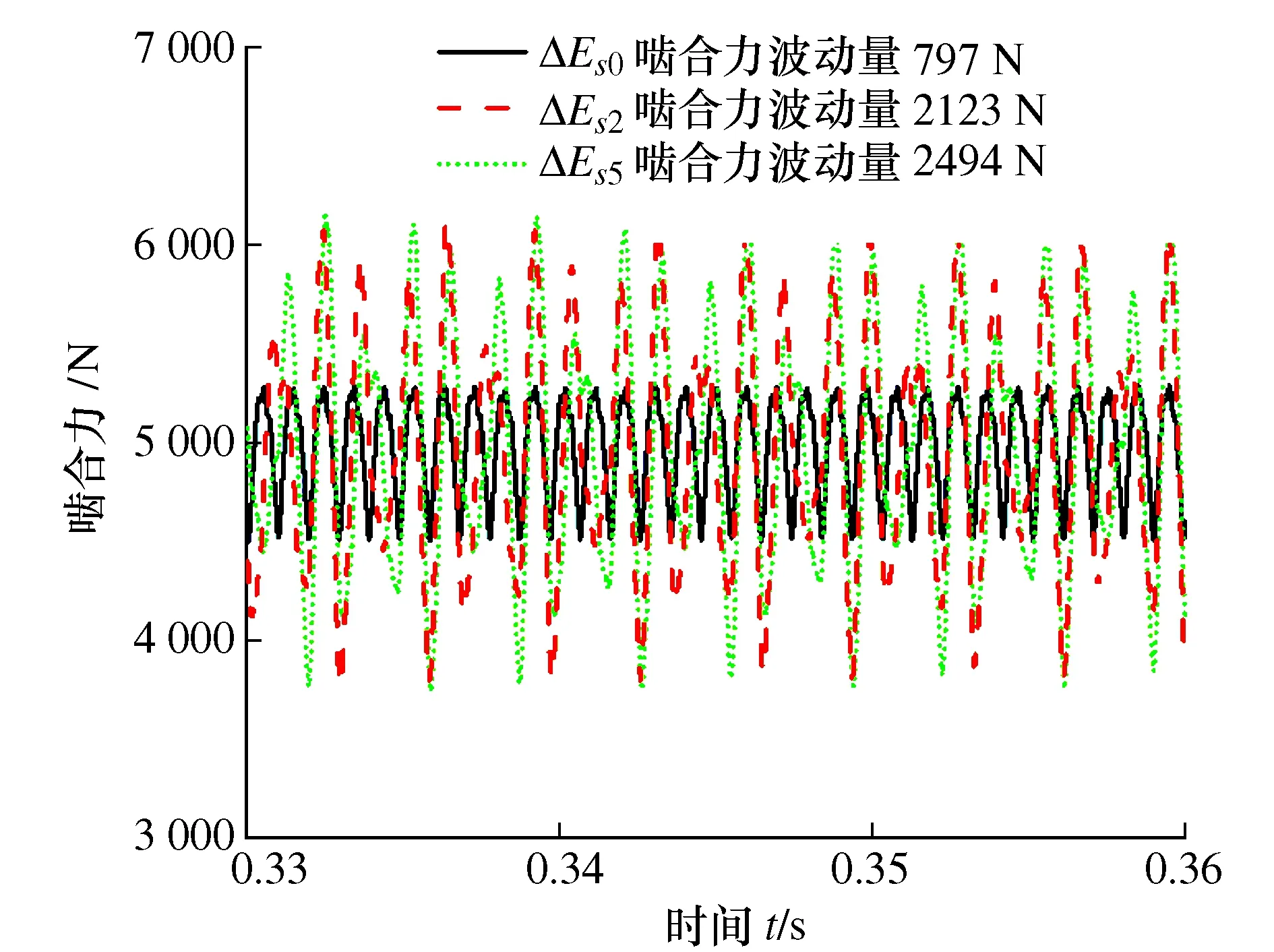
图26 作用扭矩0.5 T动态啮合力
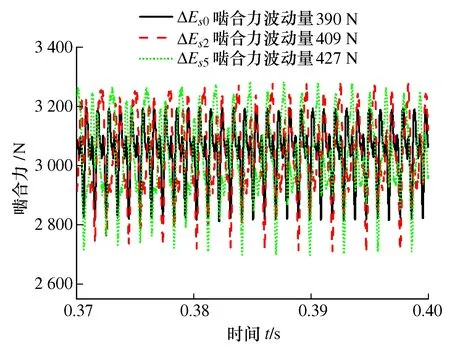
图27 作用扭矩0.25 T动态啮合力
由图25~图27可得,相同作用扭矩下,随着齿厚偏差增加,齿轮副动态啮合力波动增大,系统振动增大,这与前面的结论是一致的;相同齿厚偏差下,随着作用扭矩减小,动态啮合力波动明显减小,齿轮啮合副振动减小,同时齿轮副振动特性对齿厚偏差敏感性降低。
4 结论
1) 由于齿厚偏差的存在,圆柱齿轮副单齿啮合刚度降低,传递误差和啮合振动增大。
2) 其他参数不变时,随着齿厚偏差量增加,圆柱齿轮副单齿啮合刚度逐渐降低,传递误差和啮合振动增大。
3) 螺旋角对圆柱齿轮副啮合状况影响显著,随着螺旋角减小,齿轮副单齿啮合刚度降低,传递误差波动量明显增大,齿轮啮合副振动增大。同时,随着螺旋角减小,齿轮副振动特性对齿厚偏差更加敏感。
4) 随着作用扭矩减小,圆柱齿轮副单齿啮合刚度降低,传递误差减小,齿轮啮合副振动减小。同时,随着作用扭矩减小,齿轮副振动特性对齿厚偏差敏感性降低。

