基于风险偏好的混合多准则群决策方法研究
武群丽, 赵 萌
(华北电力大学 经济管理系, 河北 保定 071000)
1986年,ZADEH[1]提出了模糊集理论。ATANASSOV[2]对此进行了扩展,提出了直觉模糊集的概念,受到人们的广泛关注。直觉模糊集同时考虑肯定度、反对度和不确定程度3个方面的信息,比模糊集理论考虑更加全面。直觉模糊理论已广泛应用到决策方面[3-8]。
由于单个决策者决策能力的有限性以及多准则评价值形式的多样性,混合多属性群决策方法应用而生,如直觉模糊VIOKR评价方法[4]、E-VIKOR方法[9]、MULTIMOORA决策方法[10]以及基于支持度和熵值的决策方法[11]等。目前,已有的对混合多属性群决策的研究往往基于决策者完全理性。实际上,决策者对不同方案有不同的风险偏好心理。有些学者已在决策阶段考虑风险偏好这一因素,如文杏梓等[12]以及张晓等[13]运用前景理论考虑风险偏好,赵萌等[14]建立了考虑风险态度的愿景满意度函数。通过大量的文献研究发现,绝大多数混合多属性群决策方法没有在混合数据处理和群决策两个阶段同时考虑专家的风险偏好。
基于以上问题,本文提出基于风险偏好的混合多准则群决策方法。该方法在混合数据处理和群决策两个阶段同时考虑风险偏好这一因素。在混合数据处理阶段,定义了考虑风险偏好的新记分函数,将直觉模糊数(Intuitionistic fuzzy numbers,IFNS)转化为实数。新记分函数解决了已有记分函数出现的部分问题,在比较直觉模糊数大小方面更有效。在群决策阶段,基于决策信息犹豫度和前景值偏离度两视角确定专家权重,一方面,基于专家决策信息的犹豫度来确定专家权重,考虑到各专家对不同准则决策的犹豫度存在差别,把直觉模糊数的犹豫度更加细化为3个等级,这是鲜有文献能考虑到的;另一方面,利用专家个体与群体对方案决策的前景值的偏离程度来确定权重。综合运用准则权重、专家权重、改进前景理论进行最后的决策。
1 直觉模糊集的基本概念和改进前景理论
1.1 直觉模糊集的基本概念

定义2[1]设A=〈μA(x),σA(x)〉,B=〈μB(x),σB(x)〉为两直觉模糊数,若μA(x)≥μB(x),σA(x)≤σB(x),则A≥B;当且仅当μA(x)=μB(x),σA(x)=σB(x)时,A=B。
1.2 改进前景理论
1979年,Kahneman等[15]提出前景理论,前景理论将决策者的风险偏好态度这一因素引入到决策过程中。这一理论由价值函数和概率权重函数共同组成,即
(1)
(2)
(3)
其中V表示前景价值,v(Δx)为价值函数,θ为决策方案对益损的敏感程度值,w(p)为概率权重函数,Δx表示决策方案相对于参考点的变化值。Δx≥0时,v(Δx)为收益值;Δx<0时,v(Δx)为损失值。
马健等[16]对价值函数进行了改进。改进的前景价值函数引入一个新的参数ξ,形式如下:
(4)
其中ξ、θ反映决策者对益损敏感程度。若决策者对收益更敏感,则θ=1,ξ>1;若对损失更敏感,θ>1,ξ=1。α、β反映决策者对于风险的态度,若是保守者,α、β>1;若是中间者,α、β=1;若是冒险者,0<α、β<1。
2 基于风险偏好的新记分函数
2.1 现有记分函数
1994年,Chen等[17]定义了得分函数。设任意直觉模糊数A=〈μA(x),σA(x)〉,则A的得分函数为
S(A)=μA(x)-σA(x),
(5)
其中μA(x)、σA(x)、S(A)分别表示隶属度、非隶属度、净隶属度。S(A)越高,则A越大。所以,通过比较S(A)来确定A的大小。但是,当净隶属度相同,而犹豫度不同时,则直觉模糊数的大小无法判断,式(5)忽略了犹豫度对直觉模糊数大小的影响。
牛利利等[5]把从众心理引入到函数中,提出新的得分函数
(6)
对于Chen等[17]提出的得分函数出现的无法直接比较直觉模糊数大小的情形,该函数在没有其他函数的辅助下,能够直接得出排序结果。然而,不同风险偏好类型的决策者的直觉判断是不同的,具体表现为:保守型决策者认为犹豫度越小,不确定程度越小,得到否定的机会就越小,相对风险也越小;冒险型决策者认为犹豫度越大,不确定程度越大,得到肯定的机会就越大。该记分函数考虑了风险偏好导致决策结果与人的直觉判断不符的情况。
高建伟等[6]提出了一个考虑肯定信息、否定信息以及不确定信息的新记分函数为
(7)
其中πA(x)=1-μA(x)-σA(x)。该函数表示μA(x)-σA(x)越大,πA(x)越小时,S(A)值越大,A越大。高建伟等提出的记分函数考虑了犹豫度的影响。但是,当净隶属度为零,且犹豫度不为零时,该记分函数无法比较两直觉模糊数的大小。该记分函数也没有考虑风险偏好这一因素。
罗雪鹏等[7]结合得分函数和精确函数,引入一个风险态度参数λ,定义了一种综合得分函数:
(8)
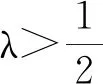
李梅[8]在考虑风险偏好及犹豫度的基础上重新定义了基于风险偏好的直觉模糊得分函数,如:
(9)
新引入的风险偏好因子η∈[-1,1]。当η>0时,决策者属于冒险型;当η<0时,决策者属于保守型;当η=0时,决策者属于中间型。此时Sη(A)退化为文献[17]的S(A)。当直觉模糊数有以下特征时,两直觉模糊数需进行二次比较:①隶属度与非隶属度其中一个为零;②净隶属度为零且犹豫度不为零。
2.2 基于风险偏好的新记分函数
基于上述分析,本文引入风险偏好这一因素,并在隶属度、非隶属度以及犹豫度的基础上重新提出一个基于风险偏好的新记分函数。新的记分函数可以解决文献[5-6]没有考虑风险偏好对决策结果影响的问题,同时可以克服文献[7-8]中的部分缺陷。
定义3 设A=〈μA(x),σA(x)〉为一个直觉模糊数,πA(x)=1-μA(x)-σA(x)为其犹豫度,则称
(10)
为A的记分函数。其中μA(x)、σA(x)、πA(x)分别表示A的隶属度(肯定信息)、非隶属度(否定信息)、犹豫度(不确定信息),μA(x)∈[0,1],σA(x)∈[0,1],πA(x)∈[0,1]。引入的风险偏好因子τ∈[-1,1],当τ>0时,决策者属于冒险型;当τ<0时,决策者属于保守型;当τ=0时,决策者属于中间型,此时Sλ(A)退化为文献[17]的S(A)。
式(10)所示的记分函数与原有记分函数有以下异同点:
相同点①在比较直觉模糊数之间的大小时,新记分函数和现有记分函数,都考虑了肯定信息、否定信息和不确定信息对决策的影响;②新记分函数与部分记分函数同时考虑了风险偏好的作用。
不同点该记分函数解决了现有记分函数3个问题:①未考虑风险偏好导致决策结果与人的直觉判断不符的情况;②有些情况下,会出现风险偏好对结果没有影响的问题;③当直觉模糊数有以下特征时,两直觉模糊数需进行二次比较,隶属度与非隶属度其中一个为零;净隶属度为零且犹豫度不为零。
下面通过两个例子进一步说明本文提出的新记分函数与现有记分函数的区别。
例1 设两个直觉模糊数分别为A1=(0.8,0.2),A2=(0.7,0),比较两数大小。用文献[5-6]及本文的记分函数计算所得结果见表1。

表1 例1的S(A)结果对比
从表1可知,文献[5-6]提出的记分函数所计算的结果没有区分风险偏好对决策结果的影响,而运用本文记分函数计算的结果可根据风险偏好类型细分为3种情况:若决策者为冒险者,A1 例2 设两个直觉模糊数分别为A1=(0,0.4),A2=(0,0.2),比较两数大小。文献[7-8]及本文的记分函数计算结果见表2。 表2 例1的S(A)结果对比 从表2可知:文献[7]的记分函数结果显示,无论决策者属于哪种类型,A1 定理1(单调性) 设A=〈μA(x),σA(x)〉为直觉模糊数,其中μA(x)∈[0,1],σA(x)∈[0,1],则记分函数Sτ(A)关于μA(x)单调递增,关于σA(x)单调递减。 证明为简述方便,以下证明将μA(x)用μ替换,将σA(x)用σ替换,将πA(x)用π替换,将Sτ(A)用Sτ替换。 定理2(有界性) 设A=〈μA(x),σA(x)〉为直觉模糊数。记分函数是有界性的,当τ∈[-1,1],记分函数满足:-1≤Sτ(A)≤1。 3.2.1 语言变量转化为直觉模糊数 在语言变量转换为直觉模糊数的过程中,很多文献没有考虑各专家对不同准则决策的犹豫度存在差别的情况,影响了决策结果的可信度。专家对同一准则给出相同的语言评价值,由于专家对各准则的了解程度并不相同,虽然将其转化为同一直觉模糊数,它们的犹豫度相同,但是不能详细地反映出专家犹豫的程度,这显然与实际不符。所以本文结合林原等[18]的转化标准,将专家犹豫度分为“很小”、“小”、“一般”3个等级。令语义评价粒度r=5,π=0.1、0.2、0.3依次表示犹豫度的3个等级,得到评价语义信息和对应直觉模糊数形式见表3。 表3 语义信息与直觉模糊数转化 3.2.2 区间数转化为直觉模糊数 假如cij=(uij,σij,πij)为aij经上述规范化处理后转化成直觉模糊数,则 (11) 鉴于事物的复杂以及专家认知的局限性,在实际决策过程中会出现准则权重信息完全未知的情况,对于此种情况,本文用综合效用最大化法[20]求解准则权重,充分考虑决策者的风险态度和心理因素。具体如下: (12) 对于形如以上模型的非线性优化问题,利用Lagrange方法求解。得到准则权重的最优解: (13) 则综合各个决策专家的平均准则权重为 (14) 专家权重很大程度上影响着最终决策结果的合理性。本文基于专家决策信息犹豫度和专家决策前景值的可靠性两个视角共同决定专家的权重。 3.4.1 专家决策信息犹豫度的权重 (15) 已知式(15),则有 (16) 专家Dl评价结果的整体犹豫度πl满足 (17) πl越大,说明专家评价的不确定程度越大,评价结果的可信任度越小,由此得到Dl的犹豫权重为 (18) 3.4.2 专家决策前景值的可靠性的权重 前景表示对方案的不同状态的选择。专家个体决策与群体决策前景值越相近,说明专家与群体对方案决策的前景值的偏离程度越低,专家决策的可靠性越强,专家赋予的权重也越大。欧氏距离来衡量两者之间的偏离程度[18],如下: (19) 专家Dl的可靠性权重可通过如下公式计算: (20) 由以上分析可得专家综合平均权重: (21) 3.5.1 混合多准则数据处理阶段 3.5.2 专家群决策阶段 (22) 式中 Step5:计算专家平均权重。 (23) Step6:按照式(24)计算综合不同偏好专家的前景值: (24) 得到整体改进前景值矩阵V=(vij)m×n。 Step7:按照式(25)计算综合改进前景值: (25) 根据vi从大到小的顺序对备选方案进行排序,vi越大,说明该方案越优。 一家电子商务公司,需要选出一个物流中心,现从4个备选物流中心(A1、A2、A3、A4)中进行选择,电子商务公司组成一个由3个专家构成的决策小组,分别为中间型D1、冒险型D2、保守型D3。评价准则为经济效益B1、自然环境B2、经营环境B3、基础设施B4、社会效益B5。决策专家经协商认为,各个准则有高等、中等、低等这3种可能的风险状态:概率分别为p1=0.1、p2=0.6、p3=0.3。试确定最优物流中心。3个专家利用区间数,语言变量,直觉模糊数的形式对准则进行打分,见表4—表6。 表4 D1的打分值 表5 D2的打分值 表6 D3的打分值 Step1、2:将混合型评价值化为直觉模糊数,直觉模糊数再转化为实数。风险偏好因子τ∈[-1,1],专家D1属于中间型,τ=0;专家D2属于冒险型,τ=1;专家D3属于保守型,τ=-1。由于篇幅限制,这里只列出专家D1高、中、低等风险状态下的直觉模糊数型打分矩阵: Step3:将各个专家评价结果的实数风险矩阵转化为改进前景值矩阵。 1)决策专家D1属于中间型,则α=β=1。令α=β=1,χ=δ=0.58,ξ=1,θ=2.25[16],得到改进前景值矩阵为 2)决策专家D2属于冒险型,则0<α、β<1。令α=β=0.88,χ=0.61,δ=0.66,ξ=1,θ=2.25[16],得到改进前景值矩阵为 3)决策专家D3属于保守型,则α、β>1。令α=β=1.21,χ=0.55,δ=0.49,ξ=1,θ=2.25[16],得到改进前景值矩阵为 Step4:准则平均权重为wj=(0.212,0.183,0.125,0.237,0.243)。 Step5:专家综合平均权重。 Step6:计算综合不同风险态度的决策专家的改进前景值,得到整体的改进前景值矩阵为 Step7:计算综合改进前景值。 vi=(0.051,-0.051,-0.333,-0.231)。 根据vi的大小可知,A1>A2>A4>A3,所以A1最优,电子商务公司应选择物流中心A1。 为了说明本文方法的有效性,利用文献[20]提出的基于前景价值函数的直觉模糊多属性决策方法与本文方法进行比较,文献[20]的方法结果为vi=(-0.09,-0.06,-0.272,-0.249),根据vi的大小可知方案的排序结果为A2>A1>A4>A3。与本文方法的排序结果相似,方案A1、A2比方案A3、A4优,而且A3都是最劣方案,说明本文方法有一定的有效性。但是,从排序结果也可以看出,A1和A2的排序结果有差异,文献[20]的方法计算结果显示A2是最优方案,而本文方法计算结果显示A1是最优方案。存在差异的原因是文献[20]的方法只是在群决策阶段考虑专家风险偏好,本文方法在混合数据处理和群决策两个阶段都考虑了专家风险偏好的影响,这说明了在两阶段考虑风险偏好对解决实际问题更具全面性。 本文提出了一种在混合多准则数据处理和专家群决策两个阶段同时考虑风险偏好的混合多准则群决策方法,在数据处理阶段,提出了一个考虑专家风险偏好的新记分函数,该记分函数根据风险偏好系数来决定专家风险偏好类型,不仅解决了现有记分函数因没有考虑风险偏好而导致决策结果出现偏差的问题,也增强了记分函数的区分度。在群决策阶段,引入改进的前景理论为决策方法对方案进行排序,改进的前景理论能够明确区分专家风险偏好类型。基于决策信息犹豫度和前景值偏离度两视角确定的专家权重,既把专家决策时的犹豫程度更加细化,也考虑了专家决策的可靠性。通过验证说明了本文方法的有效性,且具有较大的优势性。



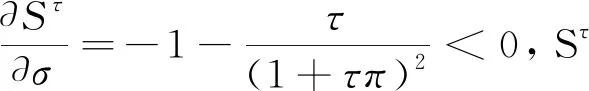

3 基于风险偏好的混合多准则群决策方法
3.1 问题描述

3.2 基于风险偏好的混合多准则数据处理



3.3 准则权重确定

3.4 决策专家权重确定



3.5 基于风险偏好的混合多准则群决策模型

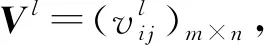



4 算例分析



4.1 混合多准则数据处理阶段
4.2 专家群决策阶段

5 结语

