不同形状类型乡村聚落道路平面形态量化研究
——以陕南地区乡村聚落为例
杨 涛
(陕西理工大学 土木工程与建筑学院, 陕西 汉中723000)
乡村聚落道路的形态特征与乡村聚落逐步占据周边适宜环境的过程密切相关,是聚落拓展过程对外部条件适应的结果与体现。准确分析乡村聚落道路形态的构成规律,既有助于对乡村聚落形态规律的深入理解,也有利于把握乡村风貌特征的来源和基础。尤其在今天乡村现代化背景下如何延续乡村特色有着更为迫切的现实意义。
乡村聚落道路形态的研究多从道路构成要素路段的形态特征和道路系统的组构特征两个方面开展。乡村聚落道路路段的研究多从空间视角对道路空间界面、比例尺度等有别于城市道路的特征进行解析。[1-8]将道路形态与聚落拓展关联起来的分析和研究鲜有涉及。
道路组构特征的研究主要是利用空间句法对道路的拓扑结构特征进行解析[9-12],偏重分析道路结构与使用者空间认知的关系,研究结果无法与道路的形态特征直接建立联系,需要进行相应的涵义诠释和转化而缺乏足够的直观性。
乡村聚落的拓展是二维层面的形态变化,为解析道路形态与聚落拓展的关系,本文所研究的道路的形态特征是二维层面的形态特征。
陕南地区以山地为主,盆地、平坝面积不足10%[13],地形地貌复杂。为适应复杂的地形条件,陕南乡村聚落在其演变拓展过程中呈现出丰富而典型的形态特征。以陕南地区的乡村聚落为对象解析道路形态,能更为准确地解析不同聚落拓展模式下道路形态的特征。因此本文以陕南地理单元内的乡村聚落为研究对象,从道路的构成要素入手,利用数理统计的方法对其平面形态特征进行量化分析,以期对乡村聚落道路平面形态的特征与聚落拓展关系进行更为精准和深入地研究。
1 研究对象与研究方法
1.1 研究对象
乡村聚落的平面形态特征是聚落在不同外部制约条件下拓展模式的体现[14]71,根据平面形状的不同可分为团状形态、带状形态和指状形态3种基本类型(见图1)。

(a)团状聚落 (b)带状聚落 (c)指状聚落
本文按照上述3种形状类型的聚落选择陕南地区安康市和汉中市部分有代表性的村落作为研究对象。以研究对象的地形图、卫星影像图为基础,结合现场调研,对相关数据进行整合与校准,绘制研究所需要的矢量图形。研究对象的基本情况见表1。

表1 研究对象一览表
1.2 研究方法
1.2.1 道路分级
对道路构成路段的形态特征进行解析,就涉及到基于何种原则对道路系统进行分解。乡村道路的修筑重视道路与建筑的联系,传统的城市规划中的道路分级方式并不适合于乡村聚落的道路研究。本文对于乡村道路的分级,不以干道道路为基准级,而是以直接连接聚落中住宅的道路为基准级(即第1级道路),同时借鉴河流分级中的Horton法[15],以仅接纳第1级道路的为第2级,接纳第1、2两级道路的为第3级。若道路接纳不同等级的上一级道路,以所接纳的等级最高的上一级道路来确定本级道路的级别。本文乡村道路的分级方式如图2所示。

图2 道路分级示意图
1.2.2 道路指标选择及计算
反映道路二维层面的形态指标有道路的长度、方向等。除此以外,乡村聚落道路平面形式的曲折多变,既是道路在聚落拓展过程中对外部条件适应的表现,也是乡村道路与城市街道差异的所在。因此本文还引入曲折度作为乡村聚落道路平面形态特征的描述指标。
(1)道路长度。道路长度是聚落拓展能力的体现,表明道路延伸、拓展到外部环境的深度。本文按道路等级分别统计其实际长度。
(2)道路角度。本文以道路的角度来表征道路拓展和延伸方向。以道路交点为基点,正东向为0度基准线,指向道路的自由端与基准线逆时针方向的夹角为道路角度(如图3所示)。

图3 道路角度测量示意图
(3)道路曲折度。道路曲折度用道路的直线率来表征,也就是用道路端点直线距离和道路实际长度的比值来表征,计算公式为[16]
(1)
式中T1为道路曲折度,l1为道路端点直线距离,L1为道路端点间的实际长度。
1.2.3 聚落平面形态指标选择与计算
本文选择聚落平面长宽比、形状指数、建筑密度表征聚落平面形态特征。聚落平面形状长宽比是指聚落平面形状长轴与短轴的比值[14]72,该比值按照文献[14]的研究方法,由聚落平面最小外接矩形求得(如图4所示)。聚落平面形状长宽比是从整体趋势对聚落拓展的反映。

图4 聚落平面形状长宽比计算示意图
形状指数是将所研究图形的周长与等面积的圆形的周长进行比较,来反映该图形相对于标准的紧凑图形的复杂变化程度,是表征聚落平面拓展的重要形态指标。其值越大表明聚落平面非均衡拓展程度越高。形状指数的计算公式为[14]76
(2)
其中S为聚落平面形状指数,P为聚落平面形状周长,A为聚落平面形状的面积。
建筑密度为聚落内的建筑基底面积与聚落面积的比值,表征的是聚落内建筑的密集程度,计算公式为
N=Ab/A,
(3)
其中N为聚落内建筑密度,Ab为聚落内所有建筑的基底面积之和。
1.2.4 数据分析
(1)基本数据统计采用Excel 2013计算。
(2)角度的多样性分析采用香农-威纳指数(Shannon-Weiner)描述,计算公式为
(4)
式中H′为多样性指数,Pi表示某形态指标第i级别内样本份数占总份数的百分比。本文将道路角度按每30°为一个区间分为12个区间,分别统计不同形状类型的聚落在每个区间道路的数量及占比,再根据式(4)计算不同形状类型聚落道路角度的多样性指数。
(3)通过单因素方差法(One-way ANOVA)分析形态的差异显著性,显著性水平设为0.05。通过Pearson相关性分析解析聚落平面形态指标与道路形态指标的相关关系。
2 结果分析
2.1 不同形状类型聚落的道路等级构成
从不同形状类型聚落道路的等级构成统计数据(见表2)可以发现:团状聚落的道路等级最多,有6级道路,指状聚落的道路等级最少,仅有4级,表明团状聚落相比其他两种形状类型聚落拥有更为复杂的道路系统。
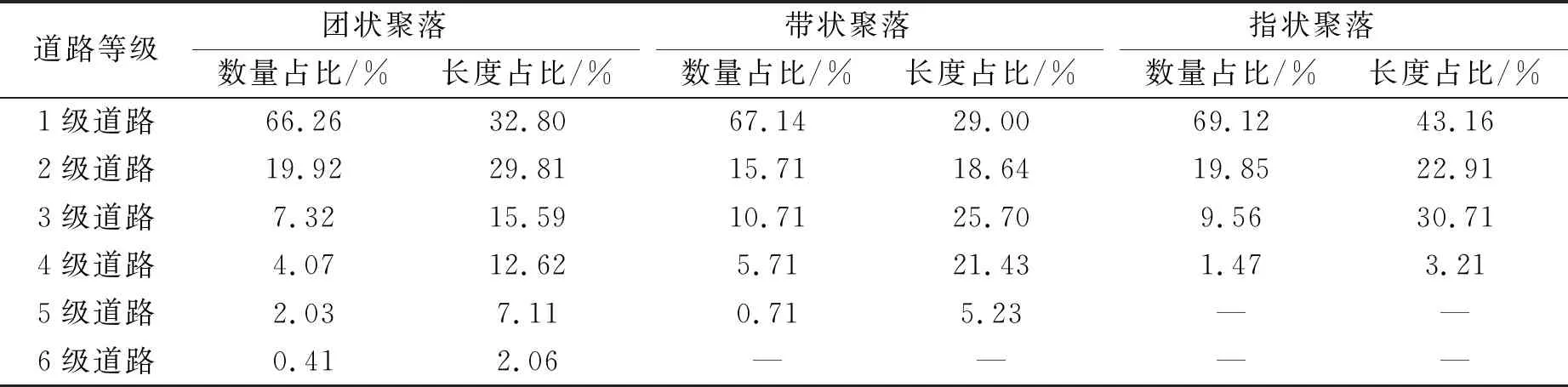
表2 不同形状类型聚落道路等级构成统计结果
在数量占比方面,3种形状聚落的1级道路数量最多,占比均超过60%,表明道路系统外部连接远多于内部连接,研究样本聚落的道路系统表现出较强的外向拓展性的特点。
由于6级道路、5级道路数量较少,本文未对上述等级道路进行两两对比分析。从表3可知,指状聚落1、3级道路的长度和团状聚落、带状聚落存在显著差异。3种形状类型聚落道路长度的变化表现出相似性,即道路的长度均随道路等级增高而增大。其中团状聚落、带状聚落4级道路最长,指状聚落3级道路最长。
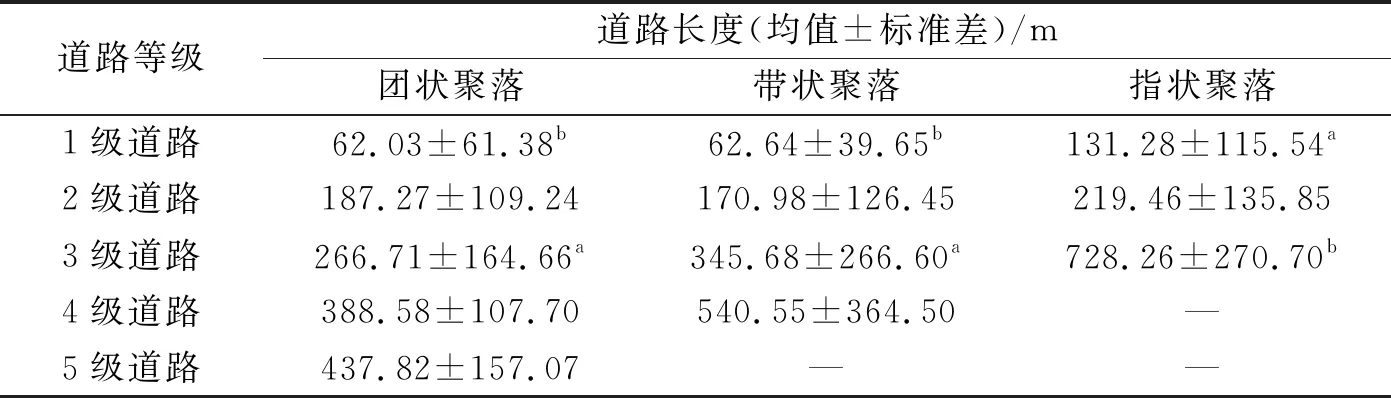
表3 不同形状聚落不同等级道路的长度
2.2 不同形状类型聚落的道路长度
不同形状类型聚落的道路长度统计结果(表4)表明,指状聚落的道路最长,平均长度为208.06 m;团状聚落的道路最短,平均长度为125.48 m;带状聚落的道路介于两者之间,道路平均长度为144.40 m。指状聚落的道路长度和其他两种形状聚落的道路长度存在显著差异(P<0.05)。

表4 不同形状类型聚落道路的长度
统计各形状类型聚落不同长度道路数量情况(图5):团状聚落和带状聚落以长度0~100 m的道路为主,该区间道路数量分别占所属类型聚落道路总数的63.82%(团状)和63.57%(带状);指状聚落则是以0~300 m的道路为主,该长度区间的道路数量占比为79.40%(指状)。

图5 不同形状聚落道路长度的数量统计图
2.3 不同形状类型聚落道路曲折度
研究样本的曲折度变化范围为0.25~1.00,其中0.9~1.0的样本占总数的73.4%,说明在条件允许的情况下,聚落道路力求接近直线,以缩短道路的长度。3种形状的聚落中,带状聚落和指状聚落道路曲折度存在显著差异(P<0.05),但与团状聚落道路的曲折度未表现出显著差异。其中指状聚落道路曲折度(0.899)<团状聚落道路曲折度(0.925)<带状聚落道路曲折度(0.944),表明带状和团状聚落的道路形态更接近直线。
随着道路等级的升高,3种形状的聚落道路的曲折度(表5)未表现出与道路等级一致的变化规律。带状聚落1级道路的曲折度和团状、指状聚落存在显著差异,其他等级的道路曲折度差异不显著。
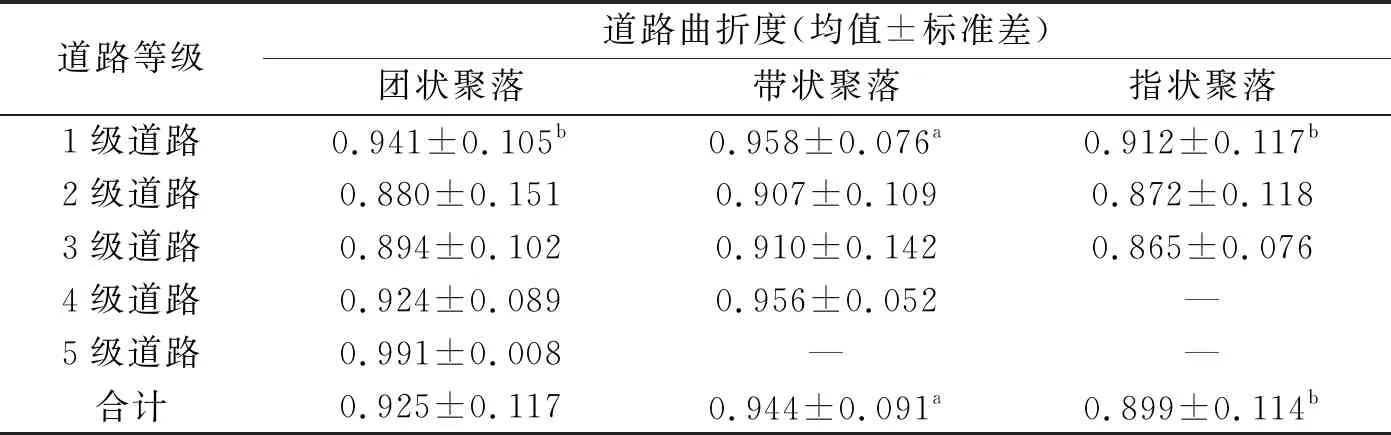
表5 不同形状类型聚落道路的曲折度
2.4 不同形状类型聚落道路角度
将道路角度按前文所说区间进行统计(表6),可以发现:区间(90°,120°]是3种形状类型聚落道路角度分布的主要区间,其他区间的道路也有相应的分布,未表现出显著差异。团状聚落道路角度的多样性最大(2.31),指状聚落道路角度的多样性最小(2.23),说明团状聚落道路角度分布更为均衡,指状聚落道路的角度在某些区间内更为集中。

表6 不同形状类型聚落道路角度分类占比及多样性指数
3种形状类型聚落道路角度(表7)的差异不显著,其中带状聚落道路角度(132.84°)<指状聚落道路角度(145.15°)<团状聚落道路角度(150.37°)。团状和指状聚落道路角度随道路等级增高逐渐减小,而带状聚落的角度则随道路等级增高呈现出“减小—增大—减小”的变化规律。
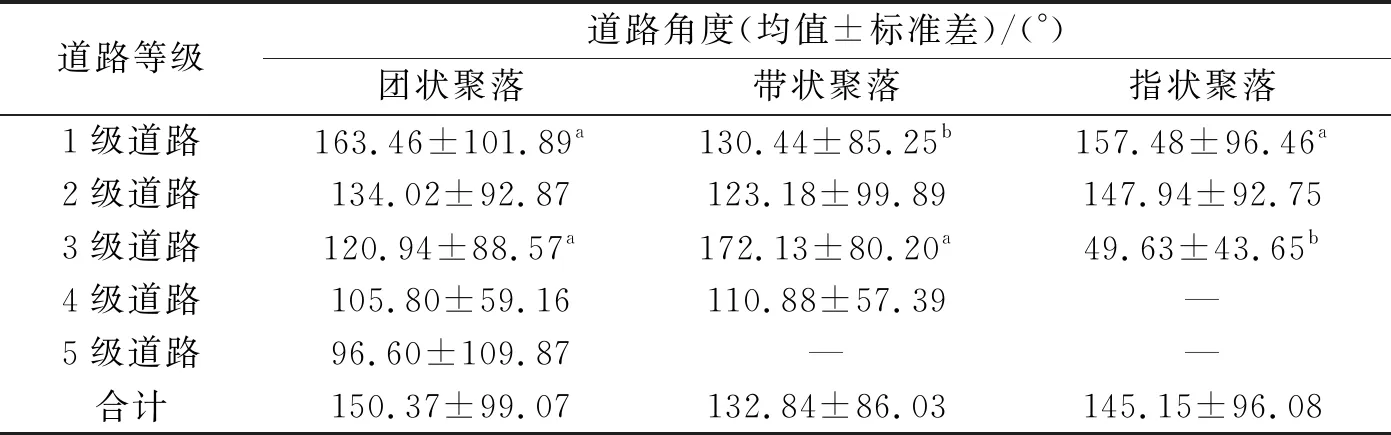
表7 不同形状类型聚落道路的角度
2.5 道路平面形态与聚落形态的相关性分析
在聚落形态与道路平面形态的相关性(表8)的分析中,仅聚落的形状指数与道路的长度存在极显著正相关(P<0.01),与道路的曲折度呈极显著负相关(P<0.01),表明聚落的非均衡拓展对道路平面形态存在显著影响。聚落平面形状的长宽比、聚落的密度均与道路平面形态指标相关性不显著,表明聚落整体的拓展趋势与内部的密集程度不会影响到道路的平面形态。

表8 聚落形态指标与道路形态指标的相关性分析
3 讨论与结论
聚落的平面形状是聚落在不同外部制约条件下拓展模式的体现。团状聚落由于缺少明显的外部制约使得内部各类资源在聚落的辐射半径相对均衡,导致外部连接的距离明显缩短,而内部连接的数量显著增加,造成路网等级构成明显多于其他两种类型的聚落。指状聚落外部条件更复杂,外部连接的距离更大,内部连接较少,使得其路网等级构成明显少于其他两种聚落形状。这一特点也反映在3种不同形状聚落的道路的长度方面:团状聚落道路长度明显小于带状和指状聚落,且长度50 m以下的道路占比最多;带状聚落道路则是50~100 m的道路占比最多;指状聚落道路长度是0~100 m的道路占比最多。表明不同形状聚落外部条件的差异使得道路长度有显著的不同。
聚落道路的曲折度是道路延伸过程中适应外部条件的体现,如避开建筑、顺应地形等。指状聚落作为3种类型中外部条件最复杂的聚落类型,其道路的曲折度要小于其他两种聚落类型,与道路要适应复杂的外部条件的情况相一致。各聚落类型中1级道路的曲折度明显大于其他级别,表明直接连接住宅的道路在条件许可的情况多选择处理成直线形态。
道路的角度反映的是道路延伸的方向和拓展范围。3种形状类型聚落中团状聚落道路的角度更大,道路的拓展范围更大,带状聚落道路的拓展范围最小,这与聚落拓展情况相一致。根据角度区间和多样性指数的分析结果,具有最大多样性指数的团状聚落道路向多个方向均匀延伸,而受到外部条件的制约,指状聚落道路只能向某些特定方向延伸。
聚落形态指标与道路形态指标相关性的分析表明,聚落整体的拓展趋势及聚落建筑的密集程度对道路的形态不会产生显著的影响,但聚落不均衡的拓展会影响到道路的长度与曲折度,或者说道路通过改变其长度,扩大占据空间的深度来聚落道路,以适应聚落的不同拓展情况,是道路形态特质差异的基础和来源。

