利用“等和线”解题

钟建新

(浙江省春晖中学 312300)

图1

当等和线恰为直线AB时，k=1；

当等和线在点O和直线AB之间时，k∈(0,1)；

当直线AB在点O和等和线之间时，k∈(1,+∞)；

当等和线过点O时，k=0；

当等和线与直线AB在点O的两侧时，则k<0.

利用等和线求解数值k(k>0)的基本步骤如下：

①连接AB，构造直线AB；

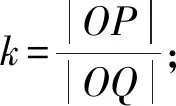
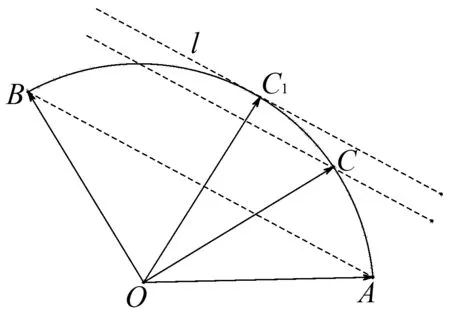
图2

所以由等和线结论得x+y的最大值是2.

例2 在ABCD中，E,F分别为CD和BC的中点，若则x+y=____.

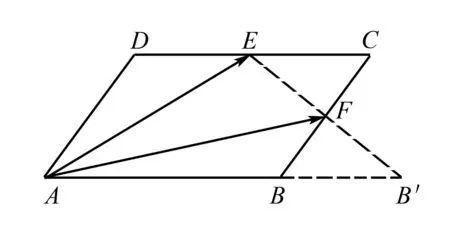
图3

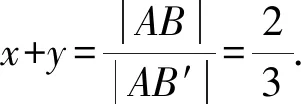
变式在ABCD中，E,F分别为CD和BC的中点，若则x+y=____.

评注若待求和的两个数不全为题设中基底的两系数，此时可构造一组新基底，使待求和的两个数分别为新基底的两系数.

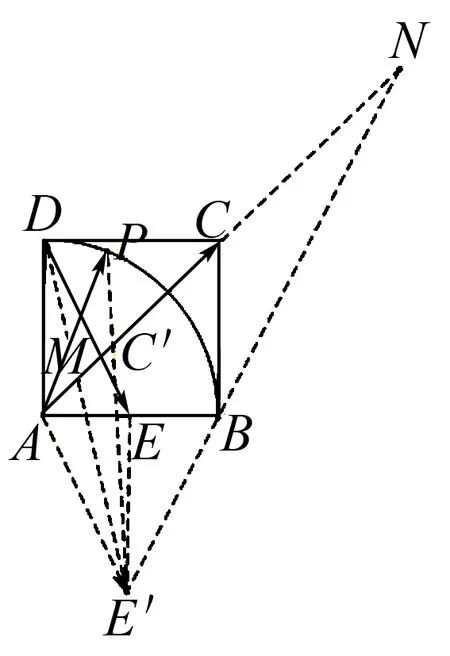
图4

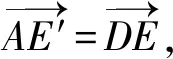
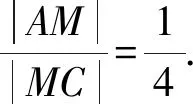
即此时x+y取到最大值5.

当点P运动到点B时，连接CE，易证得CE∥BE′.

因为E为边AB中点，

所以C为边AN中点.

评注等和线所描述的结论要求表达式中的三个向量共起点，若起点不一致，则可考虑利用向量的减法法则或者平移相关向量去统一它们的起点.

G·波利亚在《怎样解题》指出：“对于一个题目，首先要熟悉题目，我应该从哪里开始？我能做什么？这样做我能得到什么？然后深入了解题目”.只要我们对相关问题进行全面深入的研究，就会发现其解法还是有迹可循.