Quantum gravity effects on spectroscopy of Kerr-Newman black hole in gravity’s rainbow

Cheng-Zhou Liu and Jin-Jun Tao

Department of Physics, Shaoxing University, Shaoxing 312000, China

Abstract The effects of quantum gravity on spectroscopy for the charged rotating gravity’s rainbow are investigated in this paper.By utilizing an action invariant obtained from particles tunneling through the event horizon, the entropy and area spectrum for the modified Kerr-Newman black hole are derived.The equally spaced entropy spectrum characteristic of Bekenstein’s original derivation is recovered.And, the entropy spectrum is independent of the energy of the test particles, although the gravity’s rainbow itself is the energy dependent.Such that, the quantum gravity effects of gravity’s rainbow has no influence on the entropy spectrum.On the other hand,due to the spacetime quantum effects, the obtained area spectrum is different from the original Bekenstein spectrum.It is not equidistant and is dependent on the horizon area.And that, by analyzing the area spectrum from a specific rainbow function, a minimum area with a Planck scale is derived for the event horizon.At this point,the area quantum is zero and the black hole radiation stops.Thus,the black hole remnant for the gravity’s rainbow is obtained from the area quantization.In addition,the entropy for the modified Kerr-Newman black hole is calculated and the quantum correction to the area law is obtained and discussed.

Keywords: black hole, spectroscopy, gravity’s rainbow, quantum effects

1.Introduction

Black hole spectroscopy is an interesting aspect of black hole quantum properties.By studying emitted or absorbed particles of black holes,the quantization of the event horizon area with the minimum change of the horizon area asΔA=εħ was first proposed [1, 2].Hereεis a dimensionless constant,ħ is the Planck constant,and the natural unit thatc=G=1 is used.Furthermore, it was proved that, for the uniformly and slowly evolving black hole, the horizon area is an adiabatic invariant [3, 4].That is, the black hole area changes very slowly compared with the variation of external perturbations.According to the Ehrenfest principle, any classical adiabatic invariant corresponds to a quantum quantity with a discrete spectrum.Thus,black hole area can be quantized and the evenly spaced area quantum was presented as

Correspondingly, combining the area spectrum equation (1)with the Bekenstein-Hawking (B-H) entropy formula

the quantization of black hole entropy can be proved and the equidistant entropy spectrum was obtained as

In addition, using some basic properties of Euclidean black hole thermodynamics, a method of studying the black hole quantum properties was put forward [5-9].For this method, the mass and charge of black holes are treated as canonical conjugates and the time is Euclideanized.Then,by quantizing the action of black holes, the quantum spectra of different black holes are derived [5-9].

Recently, by considering the outgoing particles pass through the event horizon, an adiabatic invariant action variable for black holes was proposed as [10]

whereqiis the particles dynamic degree freedom in Euclidean coordinate,q0=τis the Euclidean time,piis the conjugate momentum.Then, applying the Bohr-Sommerfeld quantization rule

to the adiabatic invariant, the black hole spectroscopy was studied and the evenly spaced entropy spectrum equation (3)was presented [10].Hereafter, by considering the action variable to have the canonical invariance, the adiabatic invariant equation (5) was rewritten as [11, 12]

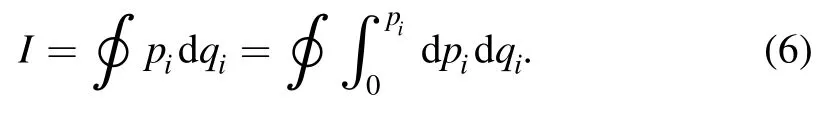
Here, the integral path closely encircles the event horizon.In previous research [10-20], by the action variable formula equations (4) and (6), the method of [10] on black hole spectroscopy has been applied to different black holes.In which,the same equally spaced entropy spectrum as Bekenstein’s spectrum equation (3) was obtained consistently.But, considering the quantum effects of black holes, the area spectrums should be different from the Bekenstein’s spectrum equation(1)and unequally spaced [10].

In this paper, using the adiabatic invariant equation (6), we study the entropy and area spectrum of the modified Kerr-Newman black hole in gravity’s rainbow.Gravity’s rainbow is a quantum corrected spacetime with a dependence on test particles energy [21, 22].The Kerr-Newman black hole is the general stationary spacetime.Our main purpose is to investigate the influence of the quantum effects of gravity’s rainbow on the spectroscopy of a charged, rotating black hole.The results show that, the spectroscopy of the rotating charged gravity’s rainbow has no energy dependence.And,the entropy spectrum is the same equidistant spectrum as the original Bekenstein spectrum equation (3).However, due to the quantum gravity effects, the obtained area spectrum is non-equidistant.And, the area spacing is dependent on the black hole area.Furthermore, by analyzing the area spectrum,the radiation remnant for the gravity’s rainbow is presented.In addition, the entropy of the modified Kerr-Newman black hole is calculated,and the quantum corrections to the B-H entropy are obtained.The relativistic units of G = Kb=c = 1 is used.

2.Gravity’s rainbow

It is generally accepted that, the existence of the minimum observable length with Planck scale should be a fundamental feature of the quantum gravity effects[23].The minimum length must remain invariant in order to preserve the equivalence principle of relativity [24, 25].This modifies the relativistic theory leading to so called Deformed Special Relativity(DSR).It is proposed that, the Lorentz algebra to incorporate the invariant length scale such that the algebra remains intact but the representation becomes nonlinear.This in turn gives a Modified Dispersion Relation (MDR) as [24-32]

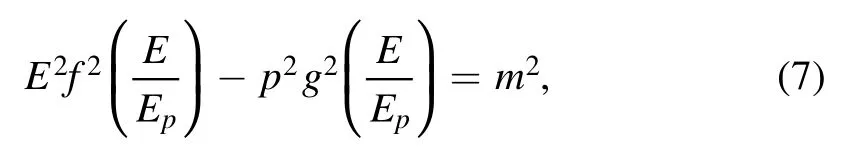
The MDR is defined in the momentum space.To give the coordinate space that is the dual to the momentum space in which the nonlinear momentum transformation exists, rainbow metrics and gravity’s rainbow takes the particle energy as parameter are proposed [21, 22].In which, the modified Schwarzschild black hole metric is given as

whereMis the mass of the black hole.It is seen that,gravity’s rainbow depends on the energy of particle moving in it.Here,the particle’s energy denotes the total energy measured at infinity from the black hole.By this,the present black hole is endowed with Plank scale effects shown as energy dependence.

As the most general stationary black hole in four-dimensional Einstein theory, the classical Kerr-Newman black hole is described by the total massM, the total angular momentumJand the total electrical chargeQas the three parameters.In gravity’s rainbow, the Kerr-Newman element can be obtained by applying transformationandfor the usual spacetime element.Thus, in Boyer-Lindquist coordinate, the modified Kerr-Newman metric in gravity’s rainbow can be expressed as [33, 34]

whereηis a positive dimensionless constant as the rainbow parameter,which is of order the unit and could be determined by experiment,nis a positive integer.The rainbow functions is motivated from a perspective of quantum spacetime phenomenology [25, 31], in which, the MDR with the effect of the minimum length is constructed as

And, the MDR is compatible with the results from Loop Quantum Gravity and non-commutative geometry [35, 36].Then, by comparing this MDR with equation (7), the rainbow functions equation(11)is proposed.In these rainbow functions,the effect off(E/Ep) which is coupled to time coordinates of the metric also vanish for the high energy particle.In the literatures, the rainbow functions equation (11) has been studied and used most widely(see[32]as a review),including the black hole quantum properties.In the present work,by using the MDR(11), we study the quantum gravity effects on black hole spectroscopy.

3.Entropy spectrum

In this part,we use the adiabatic invariant(6)to obtain the entropy spectrum of the gravity’s rainbow equation (10).To do this, we first calculate the action of the radiation particles in the black hole.It is noted that, black hole radiation is a tunneling effect with particle’s radial motion on the event horizon[37,38].But,due to the frame-dragging effects in Kerr-Newman spacetime,the matter field and the electromagnetic field in the ergosphere near the horizon must be dragged by the gravitational field[39,40].Thus,the reasonable physical picture should be depicted in the dragging coordinate system.This hints that,to write the adiabatic invariant equation (6) for the modified Kerr-Newman black hole, we should employ a dragging coordinate system.Carrying out the dragging coordinate transformation

the dragged Kerr-Newman metric in gravity’s rainbow can be obtained as

This is a three-dimensional hypersurface in the fourdimensional spacetime equation (10).Compared with the orthonormal frame equation (10) of a zero angular momentum observer, the dragged frame in equation (14) is exactly the depiction of the dragged spacetime.In fact,due to the dragging effect of the spacetime, there are no static observers near the horizon of a rotating black hole[39,40].That is to say, the particles will rotate with the rotating black hole.Then, in the commoving frame, the Kerr-Newman spacetime can be reduced from rotating to a static spacetime.That is, looking at a fixed time slices, the rotating spacetime can be considered to be the reduction from the four-dimensional to three-dimensional.The quantum tunneling is a radial transient process.Then, to calculate the tunneling action of equation (6), the reduced spacetime of equation (14) can be used.In addition, the infinite redshift surface and the event horizon of the spacetime in equation (10) is not coincident with each other, an energy layer exists between them.So the geometrical optics limit for the particles tunnel from the event horizon cannot be used.Now, by the dragging coordinate system equation (14), the infinite redshift surface is coincident with the horizons in the three dimensional hypersurface of equation (14) withgtt=0 and the geometrical limit for tunnel particles can be used.

Further, by the transformationt→iτ,withi the imaginary unit, the Euclidean metric for equation (14) can be written as

It is seen that,the coordinateφdoes not appear in the dragged coordinate system equations (14) and (15).That is, for the matter-gravity system in the rotating axisymmetric spacetime,φis an ignorable coordinate in the Lagrangian function [41, 42].

In addition, when we consider the radiation of charged particle and obtain the adiabatic invariant equation (6) in the Kerr-Newman spacetime,the effects of the electromagnetic field should be taken into account.That is,we must consider mattergravity system consisting of the black hole and the electromagnetic field.In the Kerr-Newman spacetime equation (10),the four-dimensional electromagnetic potential is

By the dragging coordinate transformation equation (13),the non-zero component of electromagnetic potential is

The Lagrangian function for the matter-gravity system is

Then, switching the order of the integral and finishing the integral on time by equations (24), (23) yields

Now,for the modified Kerr-Newman black hole,we apply the first law of black hole thermodynamics

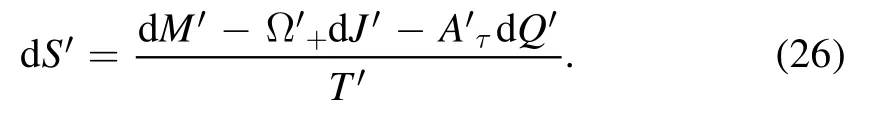
Here, the temperature of the black hole with parametersM′,J′ andQ′ isThen, equation (25) is produced as

Now, applying the Bohr-Sommerfeld quantization formula equation (5) to the action variable equation (27), the entropy spectrum for the Kerr-Newman black hole in gravity’s rainbow is obtained as

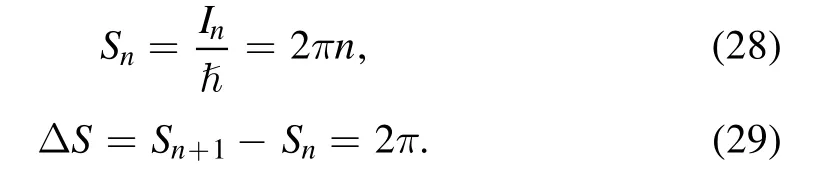
It is seen that, the entropy spectrum of the rotating gravity’s rainbow is independent of particle’s energy,despite the black hole itself has the energy dependence.And, the obtained entropy spectrum is equidistant and as the same as Bekenstein’s spectrum equation (3).Also, this is the same result as these cases from the other black holes by the action variable equations (4) and (6) [10-20].

4.Area spectrum

Now, by the present entropy spectrum equation (33), let us obtain the area spectrum.To this end, we first analyze the entropy area relation of the rotating gravity’s rainbow.For the modified Kerr-Newman black hole equation (10), keeping angular momentum parameteraas a constant [40, 41],equation (26) as the first law of black hole thermodynamics can be written as

In addition, by the null hypersurfaceΔ ≡0,the horizon radius of the modified black hole is obtained as

It is seen that, the Kerr-Newman black hole in gravity’s rainbow has the same horizons as the classical Kerr-Newman black hole.

In gravity’s rainbow, the black hole temperature can be obtained by the surface gravity in the event horizon [44-46].In this way, the temperature of the modified Kerr-Newman black hole equation (10) can be obtained as

It is seen that, the temperature has correction to the classical Kerr-Newman black hole temperature

And, the correction is related to rainbow functions and then the temperature of the gravity’s rainbow has the dependence on the energies of probe particles.

Moreover,applying the rainbow functions equation(11),the black hole temperature equation (32) can be expressed as

From the above equation, consideringηis positive, it is seen that

That is, the temperature of gravity’s rainbow is always lower than in classical general relativity.This should be an interesting MDR effect regarding the black hole thermodynamics.Of course,satisfying the redshift limit of the MDR,the usual Hawking temperature equation (33) can be recovered from the equation (34) with the limitE/Ep→ 0.However, in the high energy regime, equation (34) may have the effective distinction from equation (33).Especially, near the Planck scale, the distinction may embody the essential effects on black hole quantum properties.

In addition, in MDR, the energyEof the probe particle can be equated to the energy of particle near the event horizon, and derived from the limitation of the uncertainty principle [47, 48].Considering the momentum location uncertainty principle of particles expressed as Δp＞ ħ/Δx,there is particle energyE＞ ħ/Δx.The location uncertainty of the particles near the black hole horizon is given by the horizon radius and expressed asΔx≈r+.In this way,there is the energy of the radiation particles as [47, 48]

The particles near the event horizon constitute the Hawking radiation of black holes.Then, equation (36) means that, the characteristic energy of the test particle can be given from the black hole temperature.For Schwarzschild black hole, byand then have

Here,for the modified Kerr-Newman black hole,as a general analysis and discussion on the quantum gravity effects of black holes, we give the energy of probing particle in the same way as the Schwarzschild black hole, and use the area formula [34]

Thus, the temperature equation (34) can be expressed as

It should be pointed out that,for the Kerr-Newman black hole in gravity’s rainbow from the MDR equation (12), in order to obtain the temperature equation (39), some simplifications have been used.In equation (36), by using the Heisenberg uncertainty principle, the energy of the test particle is identified with the event radius in a heuristic way and it agrees with the temperatureT= ħ/8πM= ħ/4πr+of the Schwarzschild black hole up to a factor of 4π [47].And equation(36)can be strictly rewritten as equation(37)for the usual Schwarzschild black hole.But, for the Kerr-Newman black hole,equation(36)is not equivalence with the Hawking temperature and the equation (37) is not a strict result of equation(36).In fact,the Kerr-Newman black hole has more complicated structure, and the formula equations (36) and(37)is applied in an analogy way only by consulting the case of Schwarzschild black hole[34].This is order to simplify the calculation and the identification of particles energy with the radius or the square root of area should be treated as artificial in some sense.In addition, equation (38) is applied to the modified Kerr-Newman black hole and here also has some approximations.This means that, in gravity’s rainbow, the horizon area should be energy dependent, as the rainbow function appearing in the metric.Specifically, from equation (10) and considering equation (11), we have the horizon area

there,η=is the determinant of the induced metric on the event horizon.Obviously, the area has the dependence on the energy of the probe particle.Here, to simplify area formula (40) and the related calculations, the area (38) is used [34].That is, the zero-order approximation of rainbow functions is applied and the quantum corrections is neglected in equation (40).Thus, for convenience and heuristic considering the quantum gravity effects of complex black hole in gravity’s rainbow, from equations (36)-(39),some conjectures and simplifications have been used and these should be further clarified.

Similar to equation(38),take the angular velocity and the electricity potential on the event horizon as, respectively,

Then,substituting equations (40)-(42)into equation (30),we get

By means of the event horizon radius equation (31) and the identity

Equation (43) is written as

Substituting equation (38) into equation (45), there are

Now, combining equation (47) with the entropy spectrum equation (29), there is an area spectrum

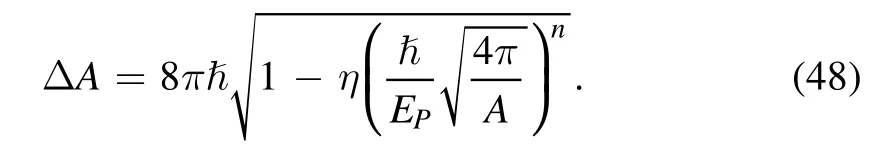
It was seen that, the obtained area spectrum for the modified Kerr-Newman black hole in gravity’s rainbow is non-equidistant and the area spacing depend on the black hole area.This is different from the original Bekenstein area spectrum equation (1), also the result equation (1) from the Kerr-Newman black hole in the classical case [13].And, the present spacing of area spectrum is smaller than the usual case of equation (1), that is

In fact, the area spectrum equation (48) can be expanded in Taylor series as

In equation (50),the first item is just the result of Bekenstein spectrum of equation (1).The subsequent items are the deviations and corrections of area spectrum to Beckenstein spectrum.But,if we ignore the quantum gravity effects of the MDR withη→0, the same result as the original Bekenstein area spectrum equation (1) can be obtained from the present area spectrum equation (48).Also, for the large black hole with scale being much larger than Planck scale, the area spectrum equation (1) in the classical case can be recovered from equation (48) byA→∞.This is consistent with the black hole area spectrum by using the action variable when considering the quantum corrections of black hole entropy [10].

5.Radiation remnant and entropy

Black hole area spectrum is related to black hole radiation[1-3].The area spectrum (48) with quantum gravity effects may reveal new phenomenon on black hole radiation.From the area spectrum (48), it is seen that, as the modified Kerr-Newman black hole radiates and area decreases, the area spacing will gradually reduce.And that, the quantum corrections on the area spectrum shown as the non-equidistance and the dependence on the area become obvious gradually.In particular, when the black hole reaches the scale with event horizon area as

there will be

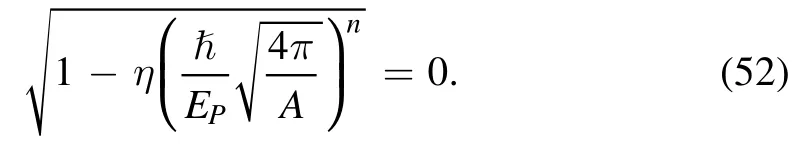
Then, from the area spectrum equation (48), we get

At this point, the area spacing disappears.And that, the zero area quanta does not mean that there is a continuous change in the area.Instead, it should show that the black hole area no longer decreases and the black hole reaches the minimum scale.Because, from equations (48), (52) and (53), it can be seen that, to require the area spectrum having the physical meaning, we need to haveA≥Amin.In other words, for the modified Kerr-Newman black hole in gravity’s rainbow,Aminis just the lower bound of event horizon area.Thus, in this way, when the event horizon area reaches the smallest valueAmin,black hole radiation should stop and the radiation remnant with areaAminappears.

Further, for the radiation remnant, from equations (51)and (37), the energy of the black hole is obtained as

That is,the mass for the remnant state iswhereMpis Planck mass.This could be interpreted as the‘zero point energy’of black hole due to the quantization of the black hole area also the Hawking radiation.

And that, from the temperature equation (39) and remnant area equation(51),the temperature for the remnant state can be obtained as

Thus, for the Kerr-Newman black hole in gravity’s rainbow,the radiation remnant with zero temperature is derived.In fact, the zero temperature also shows that, whenA=Amin,black hole radiation stops and radiation remnant appears.That is to say,while the black hole approaches the Planck scale as equation (51), the black hole temperature is zero and so the energy of the radiation particle and the change of event horizon area all are zero.So, from the quantum corrected area spectrum(48), the zero temperature as the end point of black hole evaporation is derived for the gravity’s rainbow.

The black hole remnant can give a possible resolution on the black hole information puzzle [49, 50].Also, it can be seen a serious candidate to explain the nature of dark matter[51, 52].By using the generalized uncertainty principle, the black hole remnant with a finite but maximum temperature with Planck scale can be obtained[47,48].The present black hole remnant with the zero temperature perhaps is a more reasonable and easier to understand result.And, the zero temperature as the end point of black hole evaporation is in agreement with the results on black hole remnant by the black hole heat capacity of gravity’s rainbow [34, 53, 54].

In addition, it is seen that by equation (45), the entropy area relation of the gravity’s rainbow will deviate from the B-H area law.Letting a series expansion, there is

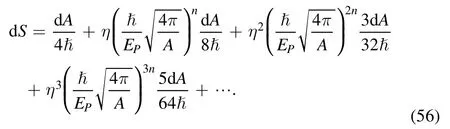
Taking the integration on the above formula,there is an entropy expression for the modified Kerr-Newman black hole as

It is seen that, considering the spacetime quantum effects,the first term of the entropy formula is just the B-H entropy,the other terms are the quantum corrections to the B-H entropy.And, the corrected terms are the power of the reciprocal of the area.As the black hole radiates and area decreases, the correction term increases.This is consistent with the quantum corrections of the black hole area spectrum equation (50).In fact,both the corrections come from the quantum effects of gravity’s rainbow, which are inherently consistent.

It should be noted that, the entropy expression equation (57) from the rainbow functions equation (12) has the dependence onn.Furthermore, it does not apply to the cases ofn=1 andn=2 due to the divergence of the expression.But, forn=1, equation (56) is

Then, using integral operation, the entropy forn=1 is derived as

Similarly, forn=2 we have

It is seen that,forn=1 orn=2, the area logarithm item of black hole entropy is presented, and the entropy equation(57)forn≥3 does not have not the logarithm item.Taking into account of the uncertainty of thenin MDR of equation (11), thus, from the constraint of requiring the logarithm entropy for gravity’s rainbow,n=1 orn=2 should be appropriated for the MDR.In addition,if the black hole area goes to zero, some divergence would appear in entropy expressions of (57), (60) and (61).This should be analyzed and may be understood that, the quantum corrected black hole entropy requires that the black hole area is not zero, thereby it supports the emergence of the black hole radiation remnant.

Besides, gravity’s rainbow has the dependence on the model of MDR and the model has some uncertainty [24-32].Then, the dependence should have some influences on the quantum effects of black hole.For instance, there is other famous rainbow function as [29, 30]

whereβis a rainbow parameter.This is compatible with the results from the hard spectrum of gamma-ray bursts at cosmological distance[29,30].Contrary to the rainbow function equation (11), for this model of MDR, the effects ofwhich is coupled to space coordinates of the metric vanish.If we employ this model, then from equation (32), the temperature of Kerr-Newman black hole in gravity’s rainbow is obtained as

It is seen that, consistent with equation (34), the temperature(63)also has the energy dependence.That is,using the quanta with different energy,an observer at infinity will probe different effective temperature for the gravity’s rainbow.And,satisfied with the correspondence principle of equation(8),at the low energy limitE/Ep→ 0,the usual temperature equation (33) can be recovered.But, the temperature of the gravity’s rainbow has the dependence on the model of MDR.And then, (63) is a different mathematical expression with equation (34) and may have some differences meaning.For instance, equation (63) does not comply with equation (35)and the temperature from equation (63) can higher than the case of usual black hole.

Black hole temperature is the basics of black hole thermodynamics.The differences of temperature (34) and (63)coming from the specific models of MDR should have some influence on the thermal properties of black holes.For the current work,it is noteworthy to consider the influence of the temperature on the quantum gravity effect of black hole spectroscopy.But,from equation (29)and its derivation, it is seen that, the entropy spectrum of the rotating gravity’s rainbow is independent of particle’s energy and the model of MDR, despite the black hole temperature have the energy dependence also the model dependence.So,in the context of rainbow functions equation (62), the entropy spectrum is the same as in the case of rainbow functions equation (11).However,from equation (30)to equation(62),it is seen that,the temperature will affect the relation of entropy and area,and then the area spectrum.So, the area spectrum has the dependence on the model of MDR.Then, the effects of the specific form of MDR on the entropy formula,area spectrum and radiation result of black hole in gravity’s rainbow, needs to be further studied.For this, the related calculations and theoretical analysis should be given in the further work.

6.Summary and discussions

Black hole spectroscopy is an important component of quantum properties of black holes.In this paper, based upon the method outlined in [10] on black hole quantization using the adiabatic invariant action variable, the influence of spacetime quantum effects on the spectroscopy of the Kerr-Newman black hole in gravity’s rainbow is investigated.The canonical invariant action variable equation (6) for the tunneling particle passing though the event horizon is calculated.Applying the Bohr-Sommerfield quantization rule to the action variable,the black hole entropy spectrum equation(29)is obtained.The present entropy spectrum is independent of the test particle energy, although the gravity’s rainbow is energy dependent.And, it is the equally spaced spectrum as the original Bekenstein spectrum equation (3).Also, this is the same result as the other entropy spectrums obtained in a different spacetime by the invariant action variable [10-20].In addition, the present entropy spectrum is independent of the test particle energy and the model of MDR, although the gravity’s rainbow is energy and MDR model dependent.This shows that, the quantum effects of gravity’s rainbow do not affect the entropy spectrum of the modified black hole.

Using the first law of black hole thermodynamics and the obtained entropy spectrum,the area spectrum for the charged rotating black hole in gravity’s rainbow is derived.Due to the spacetime quantum effects, the obtained area spectrum equation (48) is different from the original Bekenstein spectrum equation(1).Also,this is a different result from the area spectrums obtained from the invariant action variable without considering the spacetime quantum effects[10-20].And that,the present area spectrums is non-equally spaced and depended on the black hole area.This is consistent with the result of the area spectrum by the action variable considering the quantum corrections of black hole entropy [10].And,neglecting the effects of MDR, the corrected area spectrum equation (48) can return to the case of normal black holes.Then, the equidistant spectrum being same to Bekenstein spectrum equation (1) can be obtained.In addition, in accordance with the entropy spectrum, the area spectrum of the gravity’s rainbow has no the apparent dependence on the particle energy.However, different from the entropy spectrum, the present area spectrums are dependent of the model of MDR.

In addition, the obtained area spectrum equation (48)coming from the rainbow functions equation(11)shows that,as the black hole radiation, the black hole area spacing will become smaller.And,while the black hole reaches the Planck scale as equation (51), the area spacing will be zero.Moreover, the area equation (51) is the lower limit of the horizon area which has the physical signification.Thus,the minimum area and the radiation remnant with Planck scale are obtained for the gravity’s rainbow.And, the temperature of the black hole with the minimum area is zero.The zero temperature also indicates that, for the modified black hole with the minimum area,there is no radiation and the remnant appears.The present radiation remnant with zero temperature is consistent with other results on the black hole remnant by the heat capacity of gravity’s rainbow [34, 53, 54].Thus, for the modified Kerr-Newman black hole in gravity’s rainbow, the evaporation explosion and temperature divergence in the usual black hole thermodynamics is removed by the radiation remnant.In addition, the entropy for the gravity’s rainbow is calculated and the results have the quantum corrections to the B-H entropy.

The current research supports that, in different spacetimes including the charged rotating gravity’s rainbow, the black hole entropy spectrum has the universality and as the same as the original Bekenstein spectrum equation (3).In contrast, due to the spacetimes quantum effects, the area spectrum is dependent on the horizon area and has the quantum gravity corrections to the Bekenstein spectrum equation (1).Also, the area spectrum has the dependence on the model of DSR.In addition, it is implied that, the black hole spectroscopy may relate to the black hole remnant and hint at some relevance on the possible resolution on the black hole information puzzle and candidate of dark matter.

Acknowledgments

The work was supported by the Natural Science Foundation of Zhejiang Province of China (No.LY14A030001) and the National Natural Science Foundation of China(No.11373020).