Collapse arrest in a two-dimensional Airy Gaussian beam and Airy Gaussian vortex beam in nonlocal nonlinear media
Ye Chen, Lijuan Ge, Xinglin Wang and Ming Shen
1 Department of Physics, Shanghai University, Shanghai 200444, China
2 School of Physical Science and Technology, Suzhou University of Science and Technology, Suzhou 215009, China
3 Department of Applied Mathematics and Physics, Anhui Polytechnic University, Wuhu 241000, China
Abstract Propagation dynamics of a two-dimensional Airy Gaussian beam and Airy Gaussian vortex beam are investigated numerically in local and nonlocal nonlinear media.The self-healing and collapse of the beam crucially depend on the distribution factor b and the topological charge m.With the aid of nonlocality,a stable Airy Gaussian beam and an Airy Gaussian vortex beam with larger amplitude can be obtained, which always collapse in local nonlinear media.When the distribution factor b is large enough, the Airy Gaussian vortex beam will transfer into quasivortex solitons in nonlocal nonlinear media.
Keywords: Airy Gaussian beam, Airy Gaussian vortex beam, nonlocal nonlinear media,self-healing, collapse arrest
1.Introduction
Nondiffracting Airy beams [1, 2] have attracted considerable attention [3] both in linear media [4-9] and nonlinear media[10-23] during the last decade.In nonlinear media, an Airy beam with higher power (amplitude) undergoes catastrophic collapse when the strength of the strong self-trapping effect overcomes linear diffraction and self-acceleration of the beam[24].In particular, collapse occurs in both two-dimensional[24-26]and three-dimensional Airy beams[27].Physically,the collapse is induced by a strong mechanism for energy localization of the Airy beam [28, 29].The application of nonlocal nonlinearity is an effective way to prevent the catastrophic collapse of a high-dimensional Airy beam in nonlinear media[30].Nonlocality eliminates collapse in all physical dimensions for arbitrary shapes of the nonlocal response,as long as the response function is symmetric and has a positive definite Fourier spectrum [30].In previous work, with the aid of nonlocality, we obtained stable two-dimensional Airy beams, which always collapse in local nonlinear media [31].
In the area of optics, nonlocality means that the lightinduced refractive index change of a material at a particular location is determined by the light intensity in a certain neighborhood of this location [32].Nonlocal nonlinearity exists in nematic liquid crystals [33] and thermal media [34].Many works have shown that nonlocal nonlinearity greatly affects the propagation properties of self-accelerating Airy beams [35].The beam trajectory of the Airy beams is decided by the boundary conditions of a strongly nonlocal media[36].In a strongly nonlocal nonlinear media, the normalized intensity distribution of an Airy beam is always periodic [37-39].Propagation characteristics of a truncated Airy beam [40], an Airy-Laguerre-Gaussian light bullet[41],a chirped Airy beam[42],spatiotemporal Airy Ince-Gaussian wave packets[43],an inward-focusing ring Airy beam [44], and rotating elliptic vortex complex Airy solitons [45] have also been extensively demonstrated in nonlocal nonlinear media.Nonlocality[46,47]also has deep impacts on the coherent [38, 48-50] and incoherent [51] interactions of an Airy beam, leading to the formation of bound states.
The Airy Gaussian beam [52, 53] and Airy Gaussian vortex beam [54] describe, in a more realistic way, the propagation of the Airy beam, because the beam carries finite power, retains the nondiffracting propagation properties within a finite propagation distance, and can be realized experimentally to a very good approximation [52].The propagation properties of an Airy Gaussian beam [53] and an Airy Gaussian vortex beam [54] and their interactions [55]have been studied in local nonlinear media.In nonlocal media,nonlocality also affects the propagation dynamics[56]and the interactions [57, 58] of the Airy Gaussian beam.However, collapse of an Airy Gaussian beam and an Airy Gaussian vortex beam has not been studied in both local and nonlocal nonlinear media.
In this paper, we study numerically the propagation properties of a two-dimensional Airy Gaussian beam and an Airy Gaussian vortex beam in local and nonlocal nonlinear media using the split-step Fourier transform method.The numerical results show that the distribution factor b and the topological charge m of the Airy Gaussian vortex beam decide the dynamics of the self-healing and collapse of the beam.In local nonlinear media, the Airy Gaussian beam and Airy Gaussian vortex beam with larger amplitudes always collapse due to the strong self-trapping effect.Nonlocality can effectively induce a long-range attractive force, leading to the stable propagation of such beams.When the distribution factor b is large enough, the Airy Gaussian vortex beam will transfer into quasi-vortex solitons in nonlocal media.
2.Model and basic equations
Consider a two-dimensional Airy Gaussian vortex beam propagating in nonlocal nonlinear media.The slowly varying beam envelope of the Airy Gaussian vortex beam ψ(x, y, z)can be described by the normalized nonlocal nonlinear Schrödinger equation [38],
where the variables x, y, and z are the normalized transverse and longitudinal coordinates, respectively, scaled by the characteristic transverse width D and the corresponding Rayleigh range d=kD2/2 [23].Here, δn(I) is the nonlinear refractive index change of the nonlocal nonlinear media, which can be represented by the following convolutional form [59]:
Here,(x,y) is the vector spatial coordinate, and→is the normalized nonlocal response functions of the media, which satisfies the normalized condition[59].
We assume the Airy Gaussian vortex beam is in the following form [54]

where A is the amplitude of the Airy beam, w is the initial beam width of the Airy beam, b is the distribution factor[53,54]controlling the beam that tends toward an Airy vortex beam with a smaller value or a Gaussian vortex beam with a larger one, and a >0 is the decaying factor to ensure containment of the infinite Airy tail and the finite power of the Airy beam [1].Here, x0and y0decide the position (location)of the vortex center [31], and m is a topological charge that denotes the angular momentum of the vortex [54].For simplicity, we set w=1 and a=0.05 throughout this paper.
3.Dynamics of a two-dimensional fundamental Airy Gaussian beam in nonlinear media
When the topological charge m=0, equation (3) represents a two-dimensional fundamental Airy Gaussian beam.In figure 1,we plot the intensity distributions of the Airy Gaussian beam with different distribution factors b.The choice of appropriate b can make the initial beams tend toward an Airy beam with a smaller value, such as b=0.05 in figure 1(a), or a Gaussian beam with a larger value, such as b=0.3 in figure 1(d).The influences of the distribution factor b will be explored later.

Figure 1.The intensity distributions of a two-dimensional Airy Gaussian beam with different values of parameter b.The initial parameters are A=3, m=0, and b=0.05, 0.1, 0.2, 0.3 for (a)-(d),respectively.The zoom sizes of all the plots are scaled by 20d×20d,where d is the diffraction length (Rayleigh rangethe Airy Gaussian beam.
In this paper, we study the propagation properties of a two-dimensional Airy beam in nonlocal nonlinear media by direct numerical integration of equation(1)using the split-step Fourier transform method.Firstly, the dynamics of the twodimensional Airy Gaussian beam with the smaller distribution factor b=0.05 propagating in nonlinear media at different propagation distances z are displayed in figure 2.Here, the propagation distance z is also scaled by the diffraction length(Rayleigh range)[53,54].When the power (or amplitude) is small (A=3), we show in figure 2(a)that the Airy Gaussian beam self-accelerates and travels along the identical accelerating trajectory in a local nonlinear medium(σ=0) [24].In particular, the beam can propagate stably within 12d.After this, the intensity distribution of the Airy Gaussian beam will become irregular (distortion).

Figure 2.The intensity distributions of a fundamental Airy Gaussian beam (m=0, b=0.05) at different propagation distances in selffocusing nonlinear media.The amplitudes are A=3(a)and A=75(b),(c).The degrees of nonlocality are σ=0(a),(b)for local nonlinear media and σ=0.5 (c) for nonlocal nonlinear media, respectively.
By increasing the amplitude (power) of the Airy Gaussian beam (A=75) in local media, as shown in figure 2(b),we can see that the Airy Gaussian beam self-accelerates firstly, and then catastrophic collapse of the beam occurs at the propagation distance z=12d because of strong selftrapping.The collapse of the Airy Gaussian beam can be effectively prevented with the aid of nonlocality [30].For simplicity, in this paper, we consider the so-called Gaussian nonlocal response functions [59]

with a characteristic width σ, which represents the degree of nonlocality.The degree of nonlocality only depends on the physical mechanism of nonlocal media [30], such as molecule reorientation, heat or carrier transfer, etc.The Fourier transformofcan be obtained using the following calculation[30]
The Fourier transform of the Gaussian nonlocal response function indeed has a positive definite Fourier spectrum,which has been discussed in our previous work [31].Thus,the nonlocality induces an effective long-range attractive force,which can completely suppress the collapse of the Airy Gaussian beam, leading to the stable propagation of the Airy Gaussian beam even when its power is large enough.As shown in figure 2(c),we can see that the Airy Gaussian beam can propagate stably in nonlocal nonlinear media, in contrast to the collapse observed in local nonlinear media.

Figure 3.The intensity distributions of a fundamental Airy Gaussian beam(m=0,b=0.1)at different propagation distances in self-focusing nonlinear media.The amplitudes are A=3(a)and A=75(b),(c).The degrees of nonlocality are σ=0(a),(b)for local nonlinear media and σ=1.5 (c) for nonlocal nonlinear media, respectively.

Figure 4.The intensity distributions of a fundamental Airy Gaussian beam(m=0,b=0.2)at different propagation distances in self-focusing nonlinear media.The amplitudes are A=3(a)and A=75(b),(c).The degrees of nonlocality are σ=0(a),(b)for local nonlinear media and σ=3 (c) for nonlocal nonlinear media, respectively.

Figure 5.The intensity distributions of a two-dimensional Airy Gaussian vortex beam with the topological charge m=1 and the amplitude A=3.The values of parameter b are b=0.05, 0.1, and 0.2 for (a1)-(a4), (b1)-(b4), and (c1)-(c4), respectively.The corresponding vortex centers x0 and y0 are (0, 0), (-0.2, 0), (0, -0.2), (-0.2, -0.2), (0, 0), (-0.4, 0), (0, -0.4), (-0.4, -0.4), (0, 0), (-0.6, 0), (0, -0.6), and(-0.6, -0.6) for (a1)-(c4).The zoom sizes of all the plots are also scaled by 20d×20d.
It is interesting that the propagation properties of the Airy Gaussian beam in nonlinear media are related to the values of the distribution factor b.In figures 3(a)and 4(a),we show the dynamics of the Airy Gaussian beam propagating in local nonlinear media with b=0.1 and b=0.2,respectively.For a given value of the amplitude A=3, the stable propagation distances of the Airy Gaussian beam become shorter when the value of b increases.As discussed above, the stable propagation distance is z=12d with b=0.05 (figure 2(a)).However, for b=0.1, the stable propagation distance is z=6d (figure 3(a)), and it becomes only z=3d with b=0.2(figure 4(a)).
When we increase the value of the amplitude (A=75),the strong self-trapping effect overcomes linear diffraction and self-acceleration of the Airy Gaussian beam for both b=0.1(figure 3(b))and b=0.2(figure 4(b)),leading to the collapse of the beam.For the given amplitude A=75, we also find that the beam collapses within a smaller diffraction length when the distribution factor b is larger.For example,the propagation distances of collapse are 12d(Figure 2(b)),d(figure 3(b)), and 0.4d (figure 4(b)) for b=0.05, b=0.1,and b=0.2, respectively.When b is small, the Airy Gaussian beam has a long tail,and the intensity is located at both the main lobe and the tail of the beam.However, when b is big, the Airy Gaussian beam has a short tail; thus the intensity is almost entirely located at the main lobe of the beam.Thus, the self-trapping effect is stronger for a bigger b.It has also been shown that the critical power of the Airy Gaussian beam decreases as the distribution factor b increases [53].Hence, the Airy beam collapses within a smaller diffraction length when the parameter b is bigger for the same amplitude.With the aid of nonlocality, a stable Airy Gaussian beam can be obtained for both b=0.1(figure 3(c)) and b=0.2 (figure 4(c)).A larger distribution factor b always requires a larger degree of nonlocality σ.For example, the degree of nonlocality is σ=0.5 for a stable Airy Gaussian beam with b=0.05 (figure 2(c)).However,the degrees of nonlocality are σ=1.5 (Figure 3(c)) and σ=3(figure 4(c))for a stable Airy Gaussian beam when b=0.1 and b=0.2, respectively.
4.Dynamics of a two-dimensional Airy Gaussian vortex beam in nonlinear media
When the topological charge m ≠0, equation (3) represents a two-dimensional Airy Gaussian vortex beam carrying angular momentum.In figures 5 and 6,we plot the intensity distributions of the Airy Gaussian vortex beam when the topological charges are m=1 and m=2, respectively.By plotting the figures, we change both the distribution factor b and the position of the vortex x0and y0.The vortex center is located at the main lobe(x0=y0=0), the side lobe (x0=0 or y0=0), and the tail(x0≠0 and y0≠0) with different values of x0and y0.
When b=0.05, we show in figures 7(a)-(d) the propagation dynamics of an Airy Gaussian vortex beam in local nonlinear media with the topological charge m=1.We also assume that the vortex centers are located at different positions.Firstly,we numerically investigate the self-healing properties[60-62]of the Airy Gaussian vortex beam in local nonlinear media.

Figure 6.The intensity distributions of a two-dimensional Airy Gaussian vortex beam with the topological charge m=2 and the amplitude A=3.The values of parameter b are b=0.05, 0.1, and 0.2 for (a1)-(a4), (b1)-(b4), and (c1)-(c4), respectively.The corresponding vortex centers x0 and y0 are (0, 0), (-0.2, 0), (0, -0.2), (-0.2, -0.2), (0, 0), (-0.4, 0), (0, -0.4), (-0.4, -0.4), (0, 0), (-0.6, 0), (0, -0.6), and(-0.6, -0.6) for (a1)-(c4).The zoom sizes of all the plots are also scaled by 20d×20d.
Similar to the Airy vortex beam, we find that the selfhealing properties of the Airy Gaussian vortex beam also depend on the position of the optical vortex center[31,54].When x0=0 and y0=0,the vortex center is located at the main lobe of the Airy Gaussian beam.From figure 7(a), the self-healing of the Airy Gaussian vortex beam is apparent during the propagation.The main lobe is reborn at the corner again and persists undistorted.The Airy Gaussian vortex beam evolves into a new fundamental-like Airy Gaussian beam after the reconstruction.In figures 7(b)-(d),we show the self-healing properties of the Airy Gaussian vortex beam when the vortex center does not locate at the main lobe in local nonlinear media.After the self-healing process,the Airy Gaussian vortex beam turns into a fundamental Airy Gaussian beam; however, their intensity distributions are different with different x0and y0.When x0=-0.2 and y0=0,the vortex center is located at the minus x axis,and the intensity along the y axis is obviously stronger than that along the x axis.At the propagation distance z=6d, the beam realizes selfhealing, whereas the intensity along the y axis is weaker than that along the x axis after self-healing, as shown in figure 7(b).
This phenomena is induced by the internal transverse power flow of the vortex Gaussian beam [60].The power flows from the lobes along the y axis towards the lobes along the x axis to facilitate self-healing.A similar result with the parameters x0=0 and y0=-0.2 is shown in figure 7(c).When x0=y0=-0.2, as shown in figure 7(d), the intensity distribution is similar to the general Airy beam after selfhealing.However, the intensity at the main lobe deceases obviously.This indicates that when the vortex center is located at the internal lobes, the power of the main lobe will flow towards the vortex center along the 45° axis during the self-healing process [60].
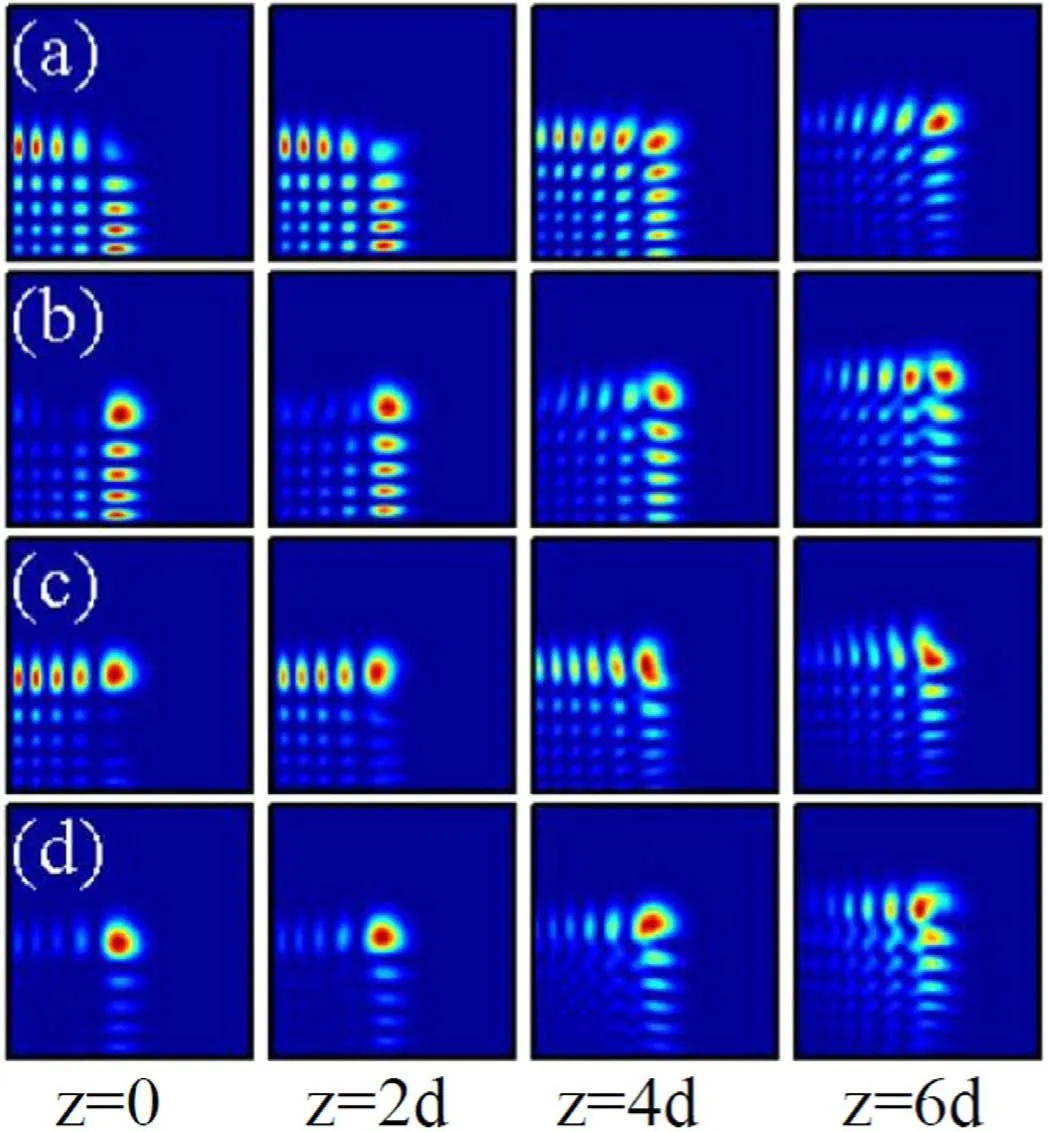
Figure 7.The intensity distributions of an Airy Gaussian vortex beam(m=1,b=0.05)at different propagation distances in local nonlinear media (σ=0).The amplitudes are A=3 for all the plots.The vortex center positions are (x0=0, y0=0), (x0=-0.2, y0=0), (x0=0,y0=-0.2), and (x0=-0.2, y0=-0.2) for (a)-(d), respectively.
Although the intensity distribution is different with different vortex center positions after self-healing, we also numerically demonstrated that the required propagation distance for self-healing does not sensitively depend on the vortex center position x0and y0when the parameters A, b,and m are given.This result can also be obtained from figure 7,which shows that the propagation distances of selfhealing are all 6d for A=3,b=0.05,and m=1,despite the fact that the vortex center positions are different.Thus, we restrict the vortex center position x0=y0=0 in the following discussions.
The self-healing properties, especially the required propagation distance of the Airy Gaussian vortex beam, are also related to the distribution factor b.When the topological charge m=1 is given, we display in figures 8(a) and (b) the self-healing of an Airy Gaussian vortex beam with b=0.1 and b=0.2, respectively.From figures 7 and 8, we find that,for an Airy Gaussian vortex beam with a larger distribution factor b, the beam very easily realizes self-healing after a smaller propagation distance.The propagation distances are 6d,3d,and 1.5d for b=0.05(figure 7),b=0.1(figure 8(a)),and b=0.2(figure 8(b)),respectively.When the value of the
distribution factor b increases, bw increases accordingly.The vortex can only destroy a little part of the main lobe of the Airy Gaussian beam.It is easy to realize self-healing within fewer diffraction lengths.
The self-healing properties of the Airy Gaussian vortex beam also have something to do with the topological charge m.For an Airy Gaussian vortex beam with smaller topological charge m=1, the beam finds it easier to realize selfhealing than that with a larger topological charge m=2 at the same propagation distance.When b=0.05,the Airy Gaussian vortex beam with m=1 has realized self-healing at z=6d(figure (7)).Although the main lobe of the Airy Gaussian vortex beam with m=2 is reborn at z=6d, the intensity of the main lobe is still weaker than the intensity of the side lobes(figure 9(a)).This phenomena also occurred for b=0.1.The Airy Gaussian vortex beam with m=1 has realized selfhealing at z=3d (Figure 8(a)), whereas the main lobe of the Airy Gaussian vortex beam with m=2 has not appeared at z=3d(figure 9(b)).An Airy Gaussian vortex beam carrying a larger topological charge always requires a longer distance(not shown) to realize self-healing due to the fact that the vortex with higher-order topological charge always destroys the beam better.
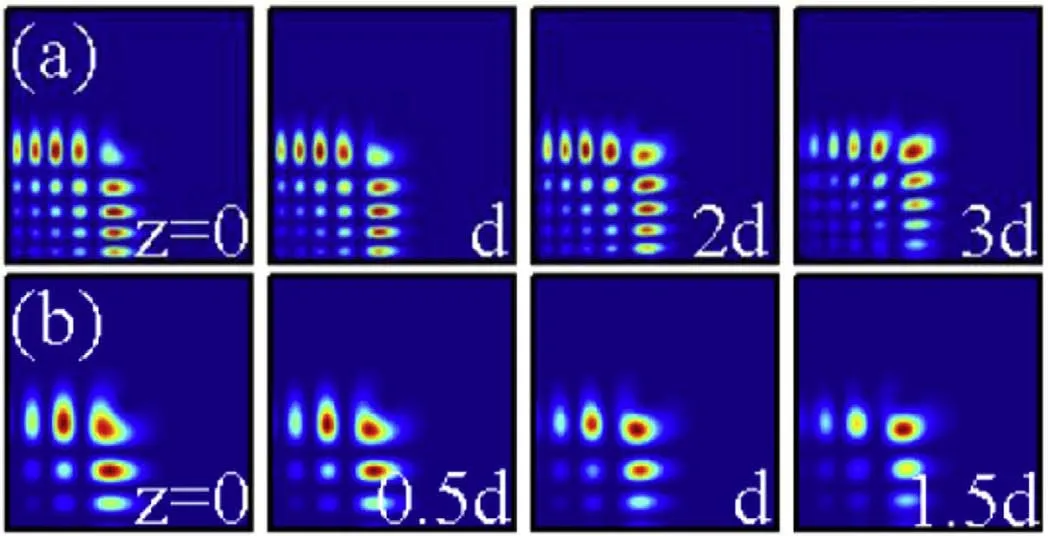
Figure 8.The intensity distributions of an Airy Gaussian vortex beam (m=1, x0=y0=0) at different propagation distances in local nonlinear media(σ=0).The amplitudes are A=3 for all the plots.The values of parameter b are b=0.1(a)and b=0.2(b),respectively.

Figure 9.The intensity distributions of an Airy Gaussian vortex beam (m=2, x0=y0=0) at different propagation distances in local nonlinear media(σ=0).The amplitudes are A=3 for all the plots.The values of parameter b are b=0.05(a)and b=0.1(b),respectively.
We increase the amplitude of the Airy Gaussian vortex beam with b=0.05 and m=1 to A=15,and the propagation of the beam is shown in figure 10(a).The Airy Gaussian vortex beam also self-heals firstly and, subsequently, selfaccelerates and travels along the identical accelerating trajectory with the propagation distance z=12d.The beam will also suffer from catastrophic collapse due to strong selffocusing effects when the amplitude is A=35,as displayed in figure 10(b).The beam realizes self-healing z=4d firstly,and then shows manifestations of a strong self-trapping process at z=8d, where its beam width decreases obviously and eventually undergoes collapse into a multi-filament pattern at z=12d.This is because the linear effects, including diffraction, self-acceleration, and self-healing, cannot balance the effects of strong self-focusing of the beam with larger amplitude (power).

Figure 10.The intensity distributions of an Airy Gaussian vortex beam(m=1,b=0.05)at different propagation distances in self-focusing nonlinear media.The amplitudes are A=15 (a) and A=35 (b), (c).The degrees of nonlocality are σ=0 (a), (b) for local nonlinear media and σ=1.5 (c) for nonlocal nonlinear media, respectively.
We also find that the dynamic is different from that of the Airy Gaussian beam (m=0) with b=0.05, which only collapses at z=12d (figure 2(b)) when the amplitude of the beam is large enough (A=75).The reason for this can be explained as follows:the stability of the vortex Airy Gaussian beam becomes worse than the Airy Gaussian beam due to the azimuthal instability of the vortex carrying angular momentum.In nonlocal nonlinear media, as shown in figure 10(c),we can obtain the self-healing and the stationary propagation of the Airy Gaussian vortex beam.
When the distribution factor b increases,the propagation properties of the Airy Gaussian vortex beam(b=0.1,m=1,and A=15) are shown in figure 11(a).The beam self-heals and self-accelerates stably with the propagation distance z=1.5d.When A=55, the Airy Gaussian vortex beam will also undergo collapse into a multi-filament pattern at z=1.5d,as displayed in figure 11(b).With the aid of nonlocal nonlinearity, we obtain, in figure 11(c), the self-healing and the collapse arrest of the Airy Gaussian vortex beam with a moderate degree of nonlocality σ=2.
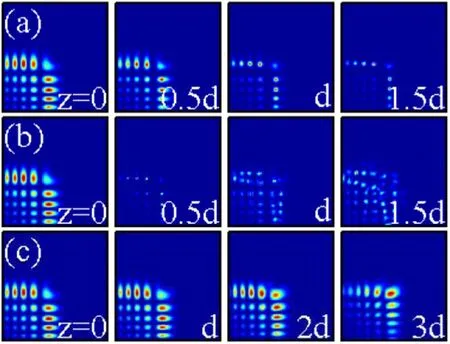
Figure 11.The intensity distributions of an Airy Gaussian vortex beam (m=1, b=0.1) at different propagation distances in self-focusing nonlinear media.The amplitudes are A=15 (a) and A=55 (b), (c).The degrees of nonlocality are σ=0 (a), (b) for local nonlinear media and σ=2 (c) for nonlocal nonlinear media, respectively.
When m=2, as shown in figure 12(a), we display the propagation dynamic of the beam in local nonlinear media with the parameters A=5 and b=0.05.It is obvious that the beam undergoes collapse into a multi-filament pattern at z=6d.The stability of the beam with higher-order topological charge becomes worse due to the azimuthal instability induced by the higher-order charged vortex.Fortunately, nonlocality can effectively induce a long-range attractive force to suppress the azimuthal instability, leading to the stable propagation of the Airy Gaussian vortex beam (figure 12(b)).

Figure 12.The intensity distributions of an Airy Gaussian vortex beam(m=2,b=0.05)at different propagation distances in self-focusing nonlinear media.The amplitudes are A=5.The degrees of nonlocality are σ=0(a)for local nonlinear media and σ=0.5(b)for nonlocal nonlinear media, respectively.
5.Dynamics of an Airy Gaussian vortex beam with larger values of distribution factor b
In this section,we focus on the propagation behavior of the Airy Gaussian vortex beam with larger values of the distribution factor b.When b=1 and m=0, as shown in figure 13(a), we can see that the Airy Gaussian beam trends to a fundamental Gaussian beam[53].The beam with smaller amplitude(A=3),is stable within a certain propagation distance (figure 13(b)) in local nonlinear media.When the amplitude increases (A=30),the beam again collapses,as shown in figure 13(c).Similarly,a stable Airy Gaussian beam can be obtained with a moderate degree of nonlocality σ=5 (figure 13(d)).

Figure 13.The intensity distributions of an Airy Gaussian beam(m=0,b=1)at different propagation distances in self-focusing nonlinear media.The amplitudes are A=3(a),(b)and A=30(c),(d).The propagation distances are z=0,0.4d,0.4d,3.2d for(a)-(d).The degrees of nonlocality are σ=0 (a), (b), (c) for local nonlinear media and σ=2 (d) for nonlocal nonlinear media, respectively.
When m ≠0, the Airy Gaussian vortex beam tends toward the conventional vortex beam when b=1.As shown in figure 14,we display the propagation dynamics of the Airy Gaussian vortex beam with the topological charges m=1 and m=2.In local nonlinear media,we can see that the beam can propagate stably within a short distance and then splits into several scalar filaments (solitons) due to the azimuthal instability of the vortex.For m=1, the beam always splits into three scalar solitons (figure 14(a)), whereas it will split into a random number of scalar solitons when m=2(figure 14(c)).This result is different from that of the conventional vortex beam, which always splits into two scalar solitons for m=1 and four scalar solitons for m=2[63,64].

Figure 14.The intensity distributions of an Airy Gaussian vortex beam (b=1)at different propagation distances in self-focusing nonlinear media.The topological charges are m=1(a),(b)and m=2(c),(d).The amplitudes are A=3(a),(b)and A=2(c),(d).The vortex centers are x0=y0=-0.25(a)-(d).The degrees of nonlocality are σ=0(a),(c)for local nonlinear media and σ=5(b),(d)for nonlocal nonlinear media, respectively.
This is because the intensity distribution of the Airy Gaussian vortex beam is not completely uniform along its ring.Thus, it is not symmetric when the azimuthal instability of the vortex breaks up the beam.With the aid of nonlocality,we can obtain a quasi-stable vortex beam,as shown in figures 14(b)and(d).Nonlocality can suppress the azimuthal instability of the vortex beam, leading to the formation of quasi-vortex solitons,where their intensity oscillates with the propagation distance.
6.Conclusion
In conclusion, we have demonstrated numerically the selfhealing and collapse arrest in a two-dimensional Airy Gaussian vortex beam in local and nonlocal nonlinear media using the split-step Fourier transform method.It has been shown that the distribution factor b and the topological charge m of the Airy Gaussian vortex beam have a deep impact on the propagation of such a beam.In the regime of strong self-trapping with a larger amplitude, a stable Airy Gaussian vortex beam can be obtained with the aid of nonlocality,which always collapses in local nonlinear media.The Airy Gaussian vortex beam will transfer into quasi-vortex solitons in nonlocal media when the distribution factor b is large enough.
Acknowledgments
This work was supported by the National Natural Science Foundation of China (No.61 975 109) and the Science and Technology Commission of Shanghai Municipal (No.19ZR1417900).
 Communications in Theoretical Physics2022年2期
Communications in Theoretical Physics2022年2期
- Communications in Theoretical Physics的其它文章
- The Sharma-Tasso-Olver-Burgers equation: its conservation laws and kink solitons
- Magnetically propelled Carreau fluid flow over penetrable sensor surface influenced by thermal radiation, Joule heating and heat generation
- Stable high-dimensional solitons in nonlocal competing cubic-quintic nonlinear media
- Few-photon routing via chiral light-matter couplings
- Effect of atmospheric turbulence on orbital angular momentum entangled state
- Persistent and enhanced spin-nematic squeezing in a spinor Bose-Einstein condensate
