一种基于大数据诊断模型的机械齿轮箱复合识别方法

吕文渊

（太原学院，太原 030012）

0 引言

现代工业快速发展，机械设备正朝向系统化、大型化发展，多种设备之间存在着紧密的联系，一旦其中个别设备出现故障将会引起相应的连锁反应，影响工业制造系统的使用效果[1]。齿轮箱作为机械制造系统的重要组成部分，已应用在工业、运输业以及农业等多个领域，其承载着机器转动中力量传递的重要作用。如此设备在运行过程中出现异常，将造成大量的经济损失，同时威胁工作人员的人身安全。因此，齿轮箱的状态识别成为机械设备维护过程中不可忽视的部分。

齿轮箱状态识别技术起源上世纪80年代的西方国家，伴随着我国经济的发展，我国也加速了齿轮箱状态识别技术的研究，尽一切可能避免事故的发生。进入21世纪以来，齿轮箱状态识别技术的有效性与准确性得到了很大的提升，但对于复合型异常识别能力相对较差，不足以支撑机械制造业的发展[2]。随着人工智能技术在各个领域中的普及，大数据技术逐渐成为机械制造业中的重点研究问题。针对当前机械齿轮箱复合识别方法对于齿轮运行数据分析能力较差的问题，构建大数据诊断模型对机械齿轮箱复合识别方法展开优化，为齿轮箱的精确识别提供有效的基础。

1 基于大数据诊断模型的机械齿轮箱复合识别方法设计

1.1 机械齿轮箱运行数据采集及处理

在大数据时代，采集到的齿轮箱运行数据是确定齿轮箱运行状态的重要依据。获取大量的齿轮运行数据，并对数据特征进行解释，成为机械齿轮箱运行状态诊断的重要组成部分。由于机械齿轮箱在日常工作环境中噪声相对较大，采集到的数据常伴有重复或缺失等问题，需要进行初次分析后，方可使用其完成后续的运算。

对部分文献进行分析后可以发现，机械齿轮箱运行异常状态大致可分为齿面胶合、轴体磨损断裂、轴体不平衡以及轴承故障等多种模式。大部分的异常运行状态会两种或是两种以上同时出现，部分异常运行状态可通过数据直接识别。但轴承故障相对较为复杂，识别精度极易受到影响。为了不对后续的识别诊断过程造成影响，使用采集到的数据计算齿轮箱轴承的振动频率，以此得到齿轮箱的运动参数。在计算前对齿轮箱的运动状态进行设定，提升计算结果可靠性：

1）齿轮大轮与齿轮小轮之间的运行模式为滚动模式；

2）齿轮箱中无形变器件

3）齿轮箱滚动轨道旋转为固定幅度

根据上述内容，对齿轮箱零件的运动特征频率进行计算。大轮在外圈的通过频率可表示为：

其中，a表示齿轮旋转角；d表示小轮直径；D表示大轮直径；ai表示大轮旋转频率；a0表示小轮旋转频率。由此公式可得到齿轮在内圈的通过频率：

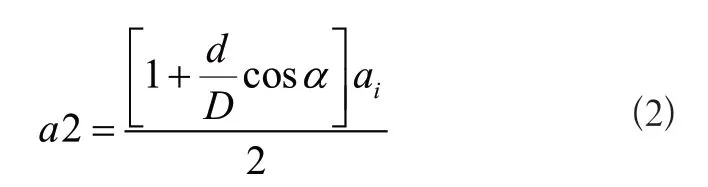
此时，保持架相对于内圈的旋转频率可表示为：

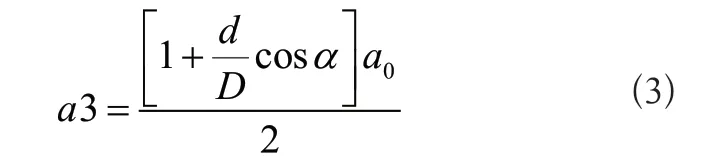
根据此公式，可得到保持架相对于外圈的旋转频率可表示为：

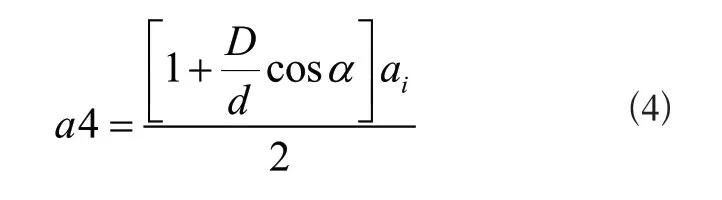
使用上述公式，对齿轮箱的运动参数进行推导，并将此部分数据结合工况环境，为后续的齿轮箱运行状态诊断提供数据基础。

1.2 机械齿轮箱运行状态特征提取

在齿轮箱运行数据初次处理结果的基础上，使用主成分分析法提取机械齿轮箱运行状态特征。将原始信号数据矢量映射为高维空间数据，实现信号类型的可划分性。在原有齿轮箱运行状态分析的过程中，多使用原始信号进行处理，导致大量的信号出现重复，影响运行状态分类效果。为避免此类问题出现在本次研究中，对数据进行预处理，剔除冗余数据，并对空位进行补位，组成新的运行数据集，并使用其完成后续的计算。在完成数据处理后，首先对处理后的信号进行归一化处理，则有：

完成归一化处理后，构建信号样本矩阵，则有：

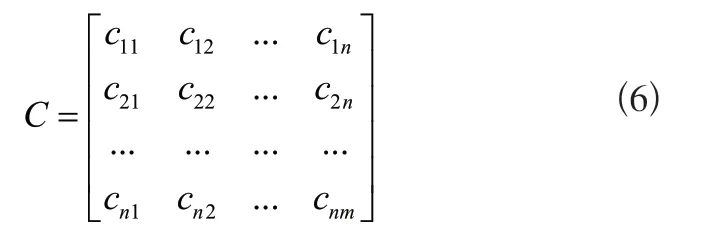
在信号矩阵中，构建变量E1，此变量约束条件设定如下：

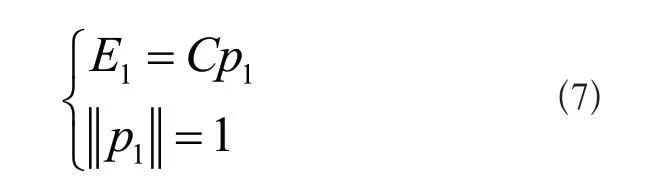
与此同时，使用变量E1对归一化处理后的信号矩阵进行处理。对式(7)进行求解时，需要将E1的方差取值结果设定为最大值。根据大数据分析相应的理论，此变量取值结果越大，则所包含的信息量越多。则E1的方差计算公式可设定为：

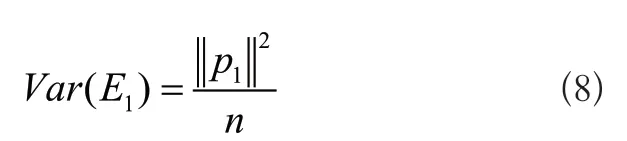
对式(6)～式(8)进行整合，构建信号信息分类拉格朗日函数[3]，则有：

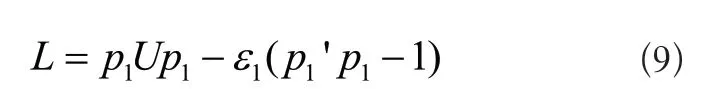
其中，U表示齿轮箱特征值；ε1表示固定计算系数。对式(9)中的偏导数进行求解，并将其设定为0，则有：

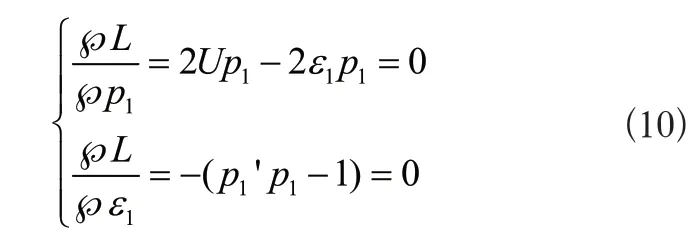
其中，p1表示U中的一个标准化特征向量，ε1表示对应的齿轮箱运行状态特征值，此时：

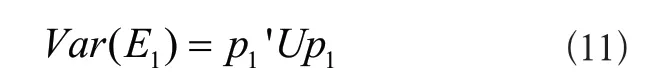
通过此公式可知，p1表示矩阵U的最大特征值，ε1表示对应的标准化齿轮箱运行状态特征向量。根据此公式，对采集到的数据进行循环计算，得到各数据的主要成分，对齿轮箱运行信息进行分类，计算过程如下所示：

根据上述公式，对齿轮箱信号进行分类。并提取每个运行状态的特征，将其作为机械齿轮箱大数据复合识别的主要判定条件。

1.3 构建机械齿轮箱大数据复合诊断模型

完成机械齿轮箱运行状态特征提取后，使用Softmax分类器[4，5]结合大数据分析技术，构建机械齿轮箱大数据复合诊断模型，实现机械齿轮箱的复合识别。

根据logistics回归模型相关原理，将Softmax分类器插入到诊断模型中。假设此模型中输入量为H=[h1，h2，…，hn]，经过Softmax分类器将H映射为H输出第i种运行状态的概率，则Softmax分类器输出结果可表示为：

其中，δ表示诊断模型计算参数；f(H，δ)表示模型最后一组输入向量第i个位置的数值；g`i表示信号数据属于第i种运行状态的置信度。

将部分异常机械齿轮箱运行状态的历史数据输入代入式(5)～式(12)中，提取此各类运行状态的特征值，将此特征值代入此模型中，给机械齿轮箱的识别过程提供参考依据。考虑到原有的机械齿轮箱识别方法仅能对单一的运行状态进行分析，在本次研究中适应交叉熵技术，提升文中诊断模型的运行类型分类能力与识别能力，则此部分计算过程可表示为：

将此公式导入诊断模型中，结合已获取到的机械齿轮箱运行状态特征对信号数据进行训练，对齿轮箱运行状态进行诊断，并输出相应的结果。对上文中的设计内容进行整理，保证运算过程的有序性与可控性。至此，一种基于大数据诊断模型的机械齿轮箱复合识别方法设计完成。

2 实验论证分析

在本次研究中提出了一种基于大数据诊断模型的机械齿轮箱复合识别方法，为证实此方法具有应用效果，构建仿真实验环节对其使用效果进行分析。

2.1 实验平台以及设备准备

本次实验中选择动力传动故障诊断综合实验台模拟动力传动系统。在此实验台中装有一个可调节转速的电机为整个实验台提供动力。与此同时，此实验台中设有一个齿轮箱，此齿轮箱中含有多个轴承与齿轮。实验台中设置了一个可编程制动装置，用以模拟实验中相关参数对实验过程的影响。综合以上内容，实验台基本结构如图1所示。

图1 齿轮箱故障诊断综合实验台

使用上述实验台，可对常见的齿面磨损、齿面胶合、轴体磨损断裂、轴体不平衡以及轴承故障进行模拟。在实验操作过程中，此实验台不仅可进行单一运行状态得到模拟，也可以同时对多个零件数据进行处理，模拟齿轮箱的复合运行异常状态，研究复合状态下的齿轮箱耦合效应。通过参数模拟的方式，为实验提供齿轮箱运行数据。针对实验数据采集工作，在本次研究中选用工业加速度传感器实现数据采集，传感器相应参数设定如下：

1）传感器灵敏度：120mV/g

2）传感器频率信号采集范围：50～300000cpm

3）测量范围：±500m/s

4）安装方式：螺栓连接

根据上述内容在实验台中安装传感器，并将此传感器的采样频率设定为50kHz，采用实验设定为0.5min。当实验台运行平稳后，通过敲打实验台的方式，模拟齿轮真实运行环境，人工噪声信号量占信号采集结果的5%。总结上述内容，并按照以上要求，完成实验台的搭建以及信号采集过程。

2.2 实验数据处理

为了对采集到的信号数据进行更加细致的分析，对齿轮箱运行状态划分，具体如表1所示。

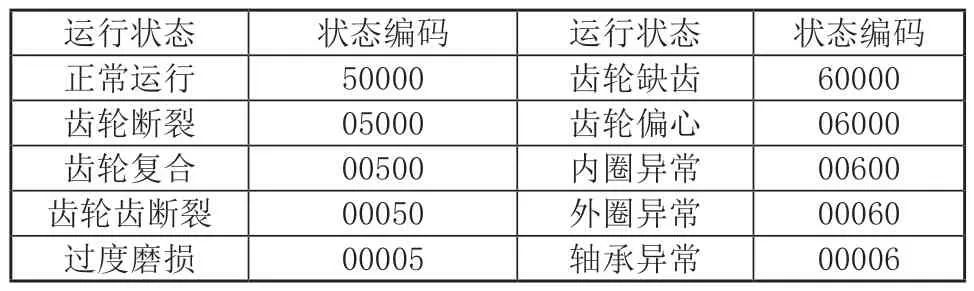
表1 齿轮箱运行状态数据统计

根据此表格，对采集到的6000条信号数据进行划分，在分类前剔除信号组中的冗余数据，得到5000条有效信号数据。在完成信号划分后，将两种或两种以上的信号数据组成一个数据组，并将此数据组作为实验中的实验样本，具体组别划分情况如表2所示。

表2 实验样本组成结构

上表中内容为本次实验中使用的样本数据，在本次实验中将其作为对本文方法进行评价的基础，设定实验操作过程，分析本文方法的使用效果。

2.3 实验操作过程及结果分析

考虑到真实齿轮箱识别环境的恶劣性，将实验信号的信噪比设定为－2db、-6db以及－10db三种环境，对本文方法的复合识别能力进行分析。为了获取更加全面的实验结果，选择LSTM识别方法以及深度学习识别方法与本文方法进行对比。在本次实验过程中，为避免计算精度对实验结果造成影响，对三种方法识别结果的平均准确率进行分析。根据以上设定，所得实验结果如图2所示。

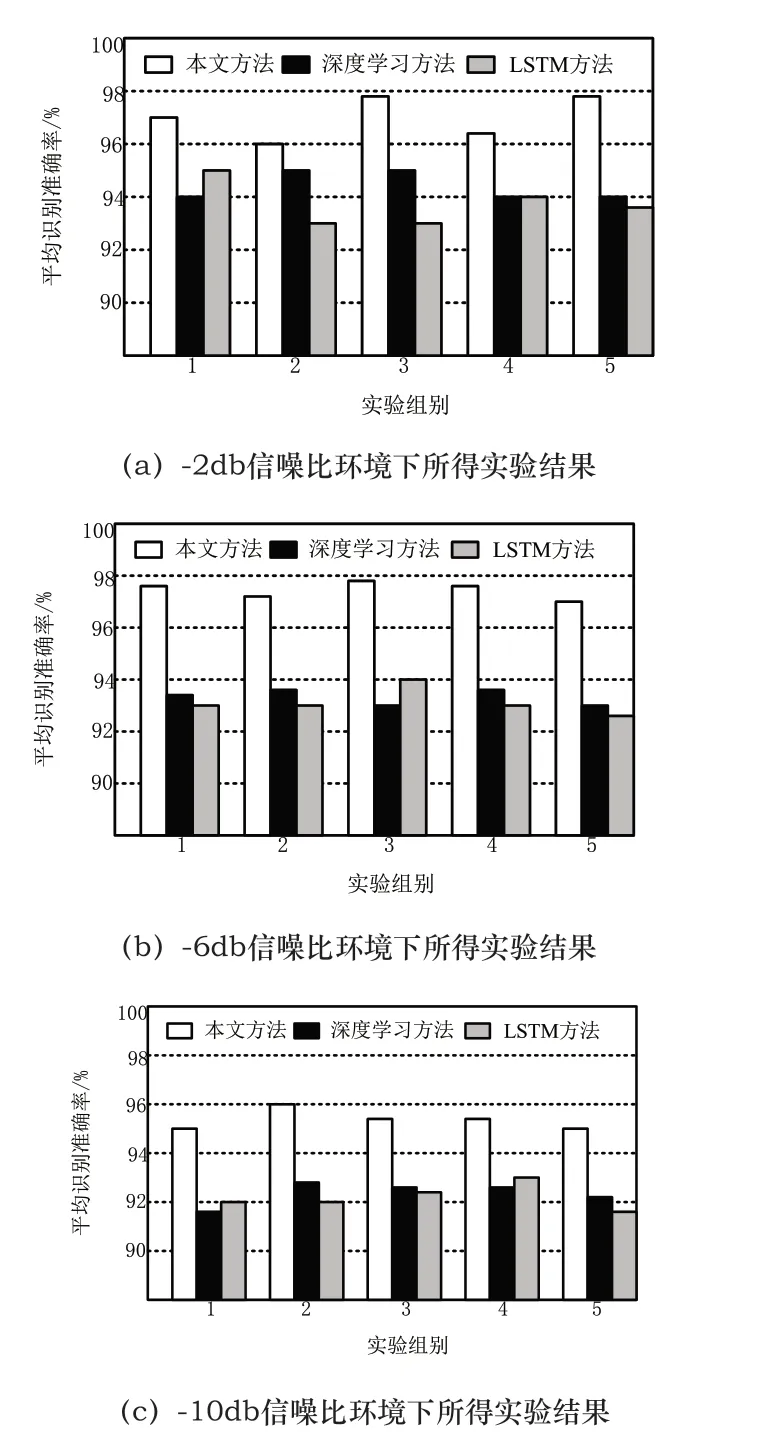
图2 识别方法仿真实验结果

对上述图像进行分析后可以看出，在不同的信噪比下，3种识别方法的使用效果具有较为明显的差异。当实验环境信噪比为－2db时，三种方法的识别率相对一致，但本文方法识别率相对较高。当实验环境信噪比下降到－6db时，本文方法的识别率未发生较大的变化，但其他两种方法的识别率逐渐下降。当实验环境的信噪比下降到－10db时，三种方法的识别精度具有较大的差异度。本文方法的识别精度固定在95.00%左右，其他两种方法的识别精度在92.00%左右。通过横向对比可以看出，本文方法相对识别精度较高。对上述三种方法进行纵向对比可以看出，本文方法的识别精度较为稳定。对上述分析结果进行整合可知，本文方法可在多种实验环境中有效控制识别精度的同时，控制方法运行的稳定性。

3 结语

在本次研究中，对大数据诊断技术与齿轮箱识别方法进行了有效的融合，并对其融合效果进行了评定。在多次实验中显示，将两种技术融合使用可有效提升齿轮箱复合识别结果的有效性。本次研究虽然在一定程度上对原有的识别方法进行了优化，但在部分领域中还存在相应的问题，在日后的研究中还需要进行不断的完善，力求为机械齿轮箱的推广应用提供动力。