基于VMD和LSTM的船舶交通流量预测方法研究

王 凯 刘 文 陈进维 刘 钊 刘敬贤

(武汉理工大学航运学院1) 武汉 430063) (武汉理工大学内河航运技术湖北省重点实验室2) 武汉 430063)

0 引 言

船舶交通流量预测是海上交通组织的基础，精确的船舶交通流量预测可为交通效率提高、航道规划优化、通航环境改善等提供坚实的理论支撑[1].

预测模型可分为线性系统模型、人工智能模型及组合预测模型[2].交通数据具有非线性、周期性和随机性等特点，线性系统模型难以获得精确的预测结果[3].基于神经网络的预测模型，通过挖掘时序数据间的复杂关系，可以提高船舶交通流量的预测精度.常见的神经网络模型有反向传播神经网络(back propagation neural network, BPNN)[4]、小波神经网络(wavelet neural network, WNN)[5]、模糊神经网络(fuzzy neural network, FNN)[6]、广义回归神经网络(general regression neural network, GRNN)[7]、长短期记忆网络(long short-term memory network, LSTM)[8]等.由于单一预测模型无法准确表征数据内在特征，通过将2种及以上模型融合构建的组合预测模型，可以结合不同模型的优势获得更加准确的预测结果.文献[9-10]通过构建组合预测模型实现数据预测，并取得了较好的效果.

LSTM模型解决了循环神经网络(recurrent neural network, RNN)的梯度消失问题，能够学习时序数据间的长期依赖关系.因船舶交通流量易受天气、航行规则等多因素的影响，统计数据往往呈现出非线性、非平稳性等特点，预测模型难以准确表征数据的内在特征，预测结果不够理想.而在LSTM模型训练过程中，损失函数是通过对网络预测结果与真实样本产生的误差反向传播指导网络调参，以得到最优的模型参数.但目前常用的损失函数并不能准确出反映两者差异，且无法兼顾鲁棒性和稳定性.

针对时序数据的非线性、非平稳性等特点，应用数据分解方法可以将时序数据分解为不同频率的子序列从而更易被模型表征其内在特征.其次，通过改进损失函数可以更加精确表现预测结果与真实样本的差异，通过网络训练以获得最优模型参数.因此，文中提出一种VMD-DTW-LSTM模型用来预测船舶交通流量.引入变分模态分解(variational mode decomposition, VMD)方法，将时序数据分解为多个不同频率尺度且相对平稳的子序列，克服经验模态分解(empirical mode decomposition, EMD)存在端点效应和模态分量混叠问题[11]，并采用动态时间规整(dynamic time warping, DTW)方法替代原始LSTM模型的损失函数，提高了预测模型的准确性及稳定性.

1 方法及原理

1.1 变分模态分解

VMD是一种完全非递归、自适应的模态变分方法.该方法可根据实际情况确定序列的模态分解个数并自适应匹配每种模态的最佳中心频率和有限带宽，实现固有模态分量(intrinsic mode function, IMF)的有效分解.克服了EMD模态分量混叠和端点效应的问题，可以降低复杂度高和非线性强的时间序列非平稳性.VMD的核心思想是变分问题的构建和求解，具体步骤如下.

步骤1构造变分问题 假设原始信号f被分解为k个分量，则对应的约束变分模型表达式为

(1)

式中：∂t为求偏导；δ(t)为狄拉克函数；K为分解模态的个数；{uk}、{ωk}分别为分解后第k个模态分量和中心频率；*为卷积运算.

步骤2为求取上述约束变分问题，引入二次惩罚因子α和拉格朗日乘法算子u(t)，将上述约束性变分问题转化为非约束性问题，增广拉格朗日表达式为

L({uk},{ωk},λ)=

(2)

步骤3应用交替方向乘子法(alternating direction method of multipliers, ADMM) 结合傅里叶等距变换寻求增广拉格朗日函数的解，其中uk、ωk、λ交替更新，N为最大迭代次数，直到满足式(3)则迭代终止.

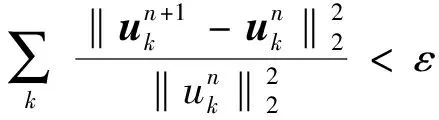
(3)

最终得到的最优解即各IMF分量的uk及中心频率ωk.

1.2 动态时间规整

W={w1,w2,…,wk,…,wK}

(4)

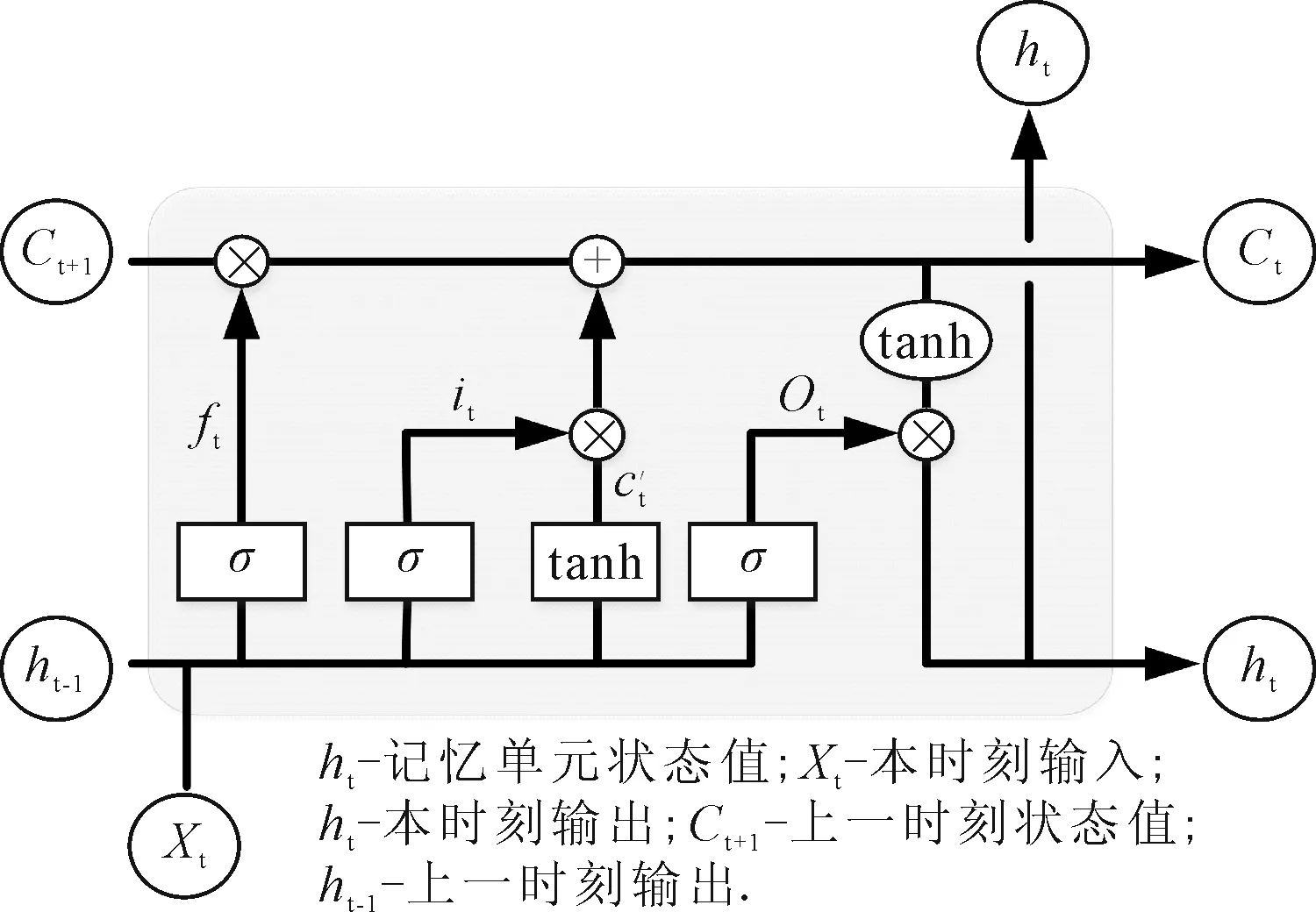
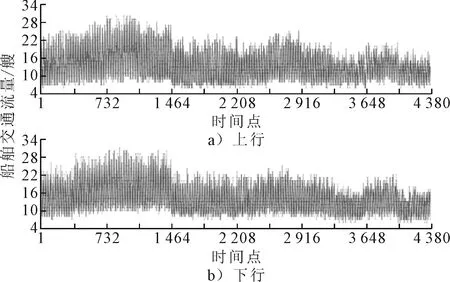
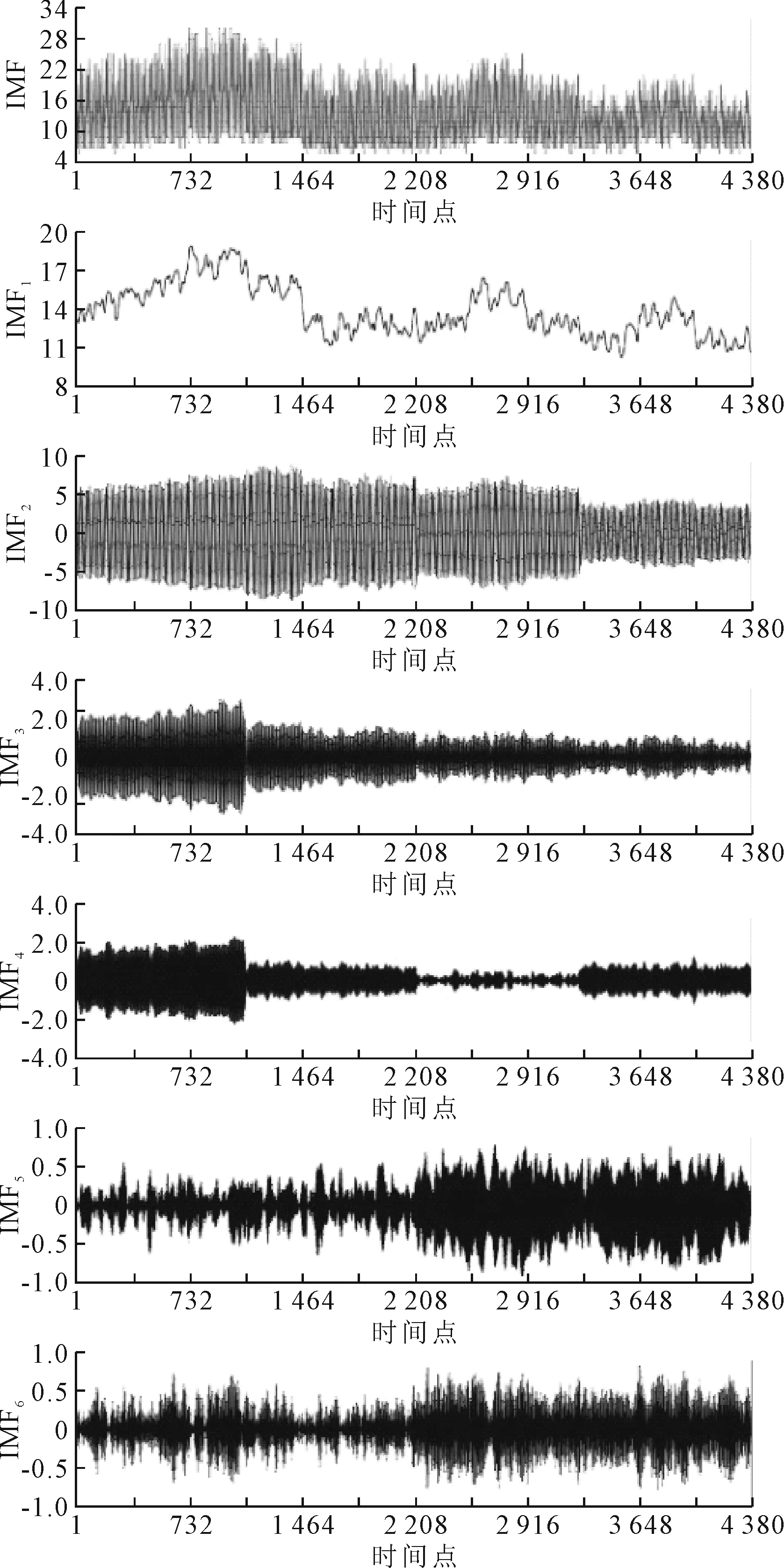
式中：K满足条件max(m,n)≤K

在寻找最佳路径的过程中，还需满足以下约束条件.

1)边界条件 即w1=(1,1)，wK=(m,n).

2)连续性 若wk-1=(x′,y′)，则下一个映射点wk=(x,y)应该满足如下条件.

x-x′≤1,y-y′≤1

(5)

即映射点不能跨过某个点去匹配，只允许和相邻的点进行匹配.

3)单调性 若wk-1=(x′,y′)，则下一个映射点wk=(x,y)应该满足如下条件.

x-x′≥0,y-y′≥0

(6)

即路径只能向前不能向后匹配.

1.3 长短期记忆网络

传统的RNN模型难以处理长时依赖问题，这是由于在模型训练过程中易产生梯度消失问题.LSTM使用记忆单元替换RNN的隐含层，其记忆单元由输入门、遗忘门及输出门控制，可以自动选择最佳滞后时间，选择性记忆历史信息，从而解决RNN因序列过长而导致的梯度消失问题，其记忆单元见图1.

图1 LSTM结构示意图

在LSTM网络中，单元值更新主要包含以下步骤.

步骤1在遗忘门中通过计算得到上一时刻信息通过的比重.

ft=σ(Wf[ht-1,xt]+bf)

(7)

式中：σ为逻辑回归中的Sigmoid函数，其值域为[0,1].

it=σ(Wi[ht-1,xt]+bi)

(8)

(9)

(10)

步骤3在输出门中，依赖计算得出的当前时刻状态ct和过滤处理得到最终输出结果ht.

ot=σ(Wo[ht-1,xt]+bo)

(11)

ht=ot*tanh(ct)

(12)

式中：Wf,Wi,Wc,Wo为权重；bf,bi,bc,bo为偏置.

2 VMD-DTW-LSTM模型构建

采用VMD方法将时序数据分解为多个不同频率尺度且相对平稳的子序列，可有效降低复杂度高和非线性强的时间序列非平稳性，使模型更易表征数据的内在特征.

将经过VMD分解后的各子序列进行归一化处理，并利用LSTM模型对各子序列单独建模进行预测.在模型训练中，传统LSTM模型的损失函数计算的是对应预测结果与真实样本的欧氏距离，并不能准确出反映两者差异，且无法兼顾鲁棒性和稳定性，因此模型训练效果往往不够理想.DTW方法利用动态规划思想计算长度不同的离散序列间相似性，并通过拉伸或压缩使序列达到最佳匹配以计算相似度.在损失函数计算中，将真实样本表示为一条时间序列，预测结果为另一条时间序列，则两序列的差值可表示为两序列的相似度，且两序列数据越接近则相似度越小，因此采用DTW方法作为LSTM模型网络训练的损失函数.

文中提出的VMD-DTW-LSTM预测模型流程图见图2.通过VMD方法将时序数据分解为不同频率的子序列，并利用DTW-LSTM模型对各子序列单独建模进行预测.由于DTW-LSTM方法的复杂度较高，为在提高预测精度的基础上同时兼顾模型计算效率，仅对高频分量部分采用DTW-LSTM方法预测.将获取的各分量的预测结果进行重构得到最终的预测结果.

图2 VMD-DTW-LSTM预测模型流程图

3 实验分析

3.1 实验数据集

本实验以2016年8月1日—2017年7月31日的武汉长江大桥断面上、下行船舶交通流量为实验数据，以2 h为时间间隔对船舶交通流量进行统计，得到两个长度为4 380的时序数据，上、下行船舶交通流量折线图,见图3.

图3 船舶交通流量折线图

3.2 VMD数据分解

在VMD方法中，分解模态数量K是重要初始参数，K过小会导致模态欠分解，K过大则导致模态重复或产生额外噪声.基于中心频率法，分别设置K=3,4,5,6,7,8进行实验，评估不同K值下每个分量的中心频率.最终确定K值为6，即将船舶交通流量数据分解为6个子序列，分解结果见图4～5.由图4～5可知，IMF1、IMF2、IMF3频率较高，为交通时序数据中的高频分量，IMF4、IMF5、IMF6频率较低，为交通时序数据中的低频分量.其中IMF1变化相对缓慢，其规律较其他模态函数更为简单；IMF5、IMF6规律性较差，显示了数据随机性特点.VMD分解有效避免了模态分量的重叠，实现了不同频率时序数据的有效分解.

图4 上行船舶交通流量VMD分解图

图5 下行船舶交通流量VMD分解图

3.3 实验对比方法与评价指标

对比实验设置是将VMD-DTW-LSTM模型与其他9种预测模型的实验结果进行对比，包括3种线性系统模型和6种神经网络模型，具体有：马尔科夫模型(MM)；灰色模型(GM(1,1))；ARIMA模型[13]；BP神经网络(BPNN)；小波神经网络(WNN)；Elman神经网络(ENN)；模糊神经网络(FNN)；广义回归神经网络(GRNN)；LSTM预测模型.

采用平均绝对百分比误差(mean absolute percent error, MAPE)作为评价指标，其范围为[0,+∞)，MAPE值越小表示模型预测效果越好，计算公式为

(13)

3.4 实验设置

根据设置对比实验比较分析，实验选取的LSTM神经网络含有3个隐藏层，每层有32个神经元.为提高测预测效果，采用Dropout正则化方法，优化器使用RMSProp，损失函数应用DTW方法，其他参数使用默认参数，最大迭代次数为1 000，当误差小于10-5时，跳出循环.数据集70%用于训练，30%用于测试.由于神经网络模型每次预测结果均有差异，采取运行10次取平均值作为最终预测结果.

主要从以下两个方面进行实验.

1)验证基于DTW方法改进的LSTM模型的船舶交通流量预测性能 通过设置DTW-LSTM模型与上述9种模型的对比实验，验证基于DTW方法改进的LSTM模型对预测性能的提升.

2)验证加入VMD方法后DTW-LSTM模型的船舶交通流量预测性能 通过设置单一模型(上述9种模型加DTW-LSTM模型)与加入VMD方法的组合模型对比实验，验证加入VMD方法对预测性能的提升.

3.5 实验结果

3.5.1基于DTW方法改进的LSTM模型

DTW-LSTM模型和其他9种模型(包括3种线性系统模型和6种神经网络模型)在最后一天12个时间段的上、下行船舶交通流量预测结果的MAPE误差平均值及标准差见表1.由表1可知，LSTM模型的MAPE平均误差和标准差均小于其他模型，而DTW-LSTM在上、下行预测误差上比LSTM分别低1.31%、1.49%，标准差则分别低0.20%、0.28%，验证了DTW-LSTM模型的准确性与稳定性.此外，在大多数情况下神经网络模型在预测误差和标准差上低于3种线性系统模型，证明了神经网络模型较线性系统模型具有更好的预测性能.

表1 上、下行船舶交通流量预测MAPE平均误差及标准差

3.5.2基于VMD方法的DTW-LSTM模型

实验1)仅验证了基于DTW改进的LSTM模型相对于传统LSTM预测性能的提升.但由于船舶交通流量受多因素影响，数据呈现非线性、非平稳性等特点.针对此问题，应用VMD方法将时序数据分解为多个不同频率尺度且相对平稳的子序列，可有效降低复杂度高和非线性强的时间序列非平稳性，使模型更易表征数据内在特征.因此，本实验在实验1)的基础上加入VMD方法，验证加入VMD方法后对DTW-LSTM模型预测效果的提升.

为对比分析单一模型与加入VMD方法后模型的预测精度，求取各模型在12个时间段上预测误差MAPE的平均值及标准差，见表2～3.

表2 上行船舶交通流量预测MAPE平均误差及标准差

表3 下行船舶交通流量预测MAPE平均误差及标准差

由表2～3可知，加入VMD方法后的组合模型的平均误差均小于单一模型，表明加入VMD方法能够有效提升模型的预测性能.VMD-DTW-LSTM预测模型在上行船舶交通流量数据上的平均误差为2.03%，比LSTM模型低3.00%，比DTW-LSTM模型低1.60%；在下行船舶交通流量数据上的平均误差为2.40%，比LSTM模型低2.50%，比DTW-LSTM模型低1.10%，且标准差低于0.90%.但是在上行船舶交通流量预测中，部分组合预测模型的标准差比单一模型高，这可能是由于上行船舶交通流量数据本身原因使模型稳定性受到一定程度的影响，但下行船舶交通流量预测的标准差较单一模型有明显降低，表明加入VMD方法对模型预测性能提升的有效性.

4 结 束 语

基于DTW方法改进的LSTM模型的预测性能优于原始LSTM模型；VMD方法能够实现数据的有效分解，使预测模型更易表征数据内在特征，加入VDM方法的DTW-LSTM预测模型的预测性能较传统LSTM模型和DTW-LSTM模型分别提升了2.50%、1.10%.

文中只考虑了船舶交通流量数据的连续性和周期性，未考虑不同区域间的空间相关性.未来工作将考虑数据的空间相关性及其随时间的变化规律，实现对时空数据的精确预测.