接头刚度对装配式综合管廊受力性能的影响分析

吴剑秋，孙 旻，冉岸绿，方兴杰

（中国建筑第八工程局有限公司 上海 200135）

0 引言

根据《城市综合管廊工程技术规范：GB 50838—2015》［1-2］规定，仅带纵向接头的预制管廊的结构内力计算宜采用闭合框架模型，对于带横向拼缝接头的预制拼装管廊截面内力的计算应考虑拼缝的影响。

目前关于装配式综合管廊横向接头的研究较少，陈智强等人［3］提出了包含抗弯刚度计算模型和抗弯承载力计算模型的预制预应力综合管廊接头设计计算方法；张姾婧等人［4］对PC钢棒连接下的预制综合管廊的接头受力性能进行了较为系统化的研究；田子玄［5］、王鹏宇等人［6］对现浇管廊接头力学行为进行了数值模拟与分析。这些研究工作主要侧重于管廊接头设计计算方法和接头力学性能试验研究［7-9］，但对不同装配方式下，管廊接头刚度取值对管廊结构受力的影响缺乏有效的分析。

本文借鉴盾构管片接头刚度的计算模型和数值模拟方法，分别采用刚度解析法和有限元数值模拟，对不同装配方式下的管廊接头抗弯刚度进行了计算。

1 装配式综合管廊接头分类

装配式综合管廊根据预制程度的不同可以分为半预制综合管廊、叠合装配式综合管廊和全预制拼装综合管廊。根据连接构件的不同，装配式综合管廊接头可分为：叠合-现浇接头、预制-现浇接头和预制接头，其中预制接头根据连接方式不同，又可分为预制螺栓接头和预制预应力接头，不同连接接头如图1 所示。本文以这四类接头为研究对象，分别采用了刚度解析法和有限元法对其抗弯刚度进行了计算。

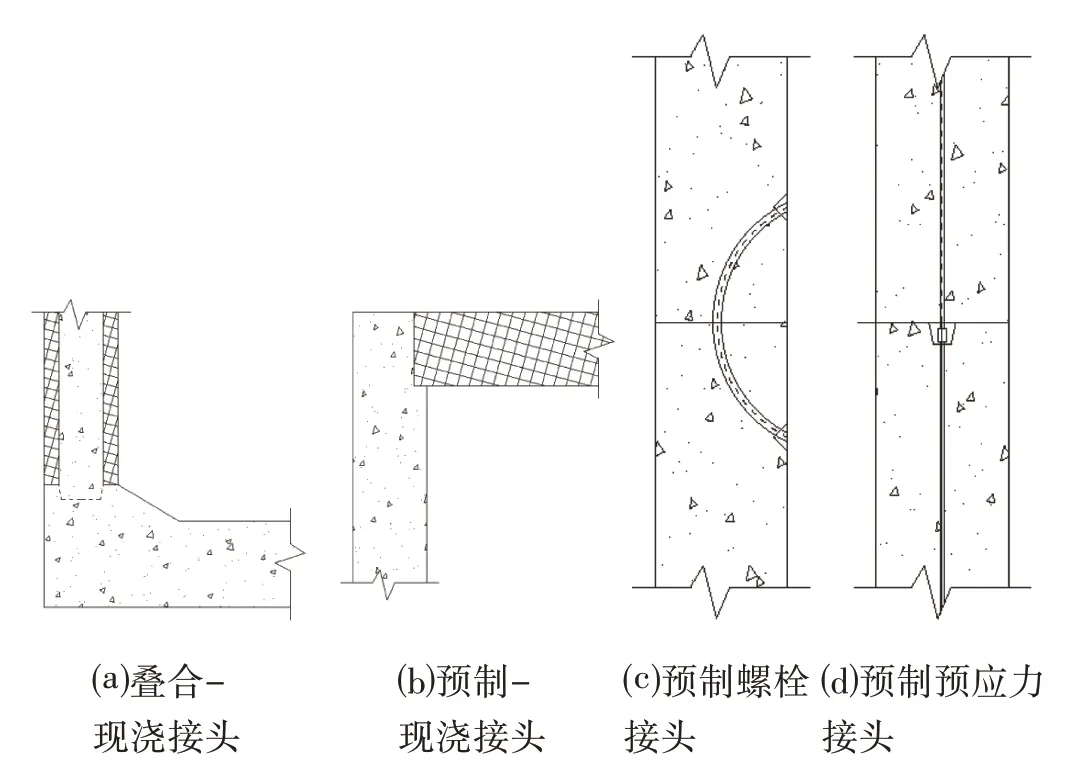
图1 装配式综合管廊接头Fig.1 Joints of Prefabricated Pipe Gallery

2 装配式综合管廊接头刚度Kθ的理论计算

管廊接头转动刚度Kθ是在接头变形方向上产生单位转角所需的弯矩，是装配式综合管廊结构计算中的关键参数。它综合反映了管廊接头在外荷载作用下的力学性能，大量设计经验表明，对Kθ取值的偏差将导致结构设计内力值出现极大差异，这样的结果将导致设计过于保守或偏于不安全。根据定义，接头转动刚度Kθ可表示为：

式中：θ为接头拼缝面转角；M为与θ相对应的接头弯矩。

目前管廊接头刚度的计算主要考虑了如下几种模型：不考虑混凝土受力的横向接头刚度计算公式、考虑混凝土压应力线性分布的横向接头刚度计算公式以及考虑混凝土压应力按抛物线分布的横向接头刚度计算公式。为了考虑混凝土变形对接头变形的影响，同时避免应用中求解非线性方程组，本文采用文献［10］中的考虑混凝土压应力线性分布的计算公式求解横向接头抗弯刚度。

2.1 基本计算假定

①假设管廊接头处的变形是由钢筋或螺栓的变形和接头断面混凝土的压缩变形所引起的；②假设接头张开后，接头端面脱离区与压缩区在各自平面上变形协调关系成立；③假设接头张开时，接头端面处受压区混凝土压应力分布形式为以接头边缘为顶点的三角形。

2.2 接头抗弯刚度计算模型

管廊接头受拉张开时，接头端面分为脱离区与受压区。接头计算简图如图2所示。此时由接头力学平衡关系得：

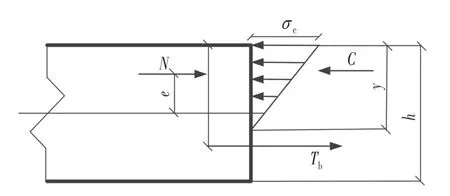
图2 接头计算模型示意Fig.2 Calculation Model of Joint

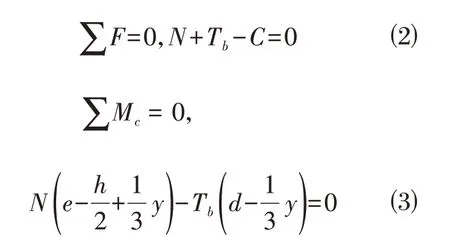
式中：N为接头轴力；e为接头内力偏心距，即接头弯矩与轴力之比；h为接头端面有效截面高度；d为螺栓或钢筋形心到接头外边缘的有效距离；Tb为螺栓或钢筋拉力，对于螺栓连接的预制综合管廊接头：

式中：n为接头计算宽度内的螺栓或钢筋根数；tb为单根螺栓拉力。

且螺栓满足物理关系：t0-tb=εbKL，其中，L为螺栓有效计算长度；K为螺栓拉伸刚度；t0为螺栓初始预应力。

对于钢筋连接的叠合装配式综合管廊接头：

式中：fy为钢筋抗拉强度设计值；As为单根钢筋计算截面积。

C=，为三角形分布的合力；σc为接头受压区边缘处的混凝土压应力；b为接头计算宽度；y为接头受压区高度。

由接头力学平衡关系和材料物理力学关系，可解得管廊接头转角θ和抗弯刚度Kθ的解析表达式。采用螺栓或预应力钢筋连接的全预制综合管廊接头转角θ和抗弯刚度Kθ的解析表达式如下：

其中，A=2γ（N+nt0）；B=［24ndN+（6Ne-3Nh）（（4n+γ）-6ndγ t0］；C=-3（8Nd-4Nh+8Ne）；γ=Ecb∕K。

采用钢筋连接的半预制或叠合装配式综合管廊接头转角θ和抗弯刚度Kθ的解析表达式如下：

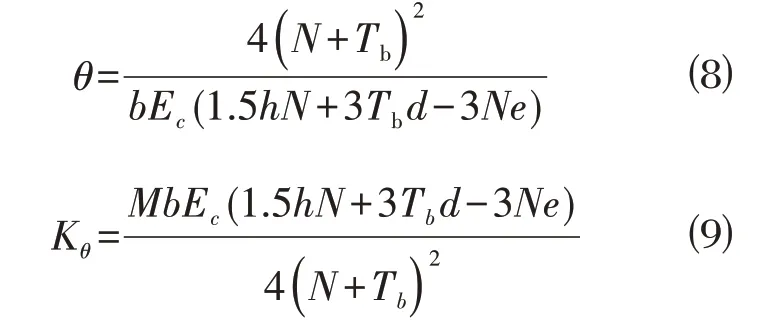
2.3 计算结果

采用式⑻、式⑼对4类管廊接头的刚度进行计算，不同接头的尺寸和基本计算参数如下：h=0.3 m，b=0.4 m，d=0.25 m，Ec=3.25×107kN∕m2，As=254.5×10-6m2，fy=360×103kN∕m2。

计算时采用3 级轴力N分别为500 kN、400 kN、300 kN，每级轴力对应5 级弯矩M分别为125 kN·m、100 kN·m、75 kN·m、50 kN·m 和25 kN·m。4 种接头不同内力组合接头M-θ关系曲线如图3所示。

由图3分析可知：在接头轴力一定的情况下，接头断面转角θ随着弯矩M的增大而逐渐增大，接头抗弯刚度Kθ，即M-θ曲线各点的切线斜率dM/dθ随着弯矩M的增大而逐渐减小，并最终趋于稳定，在管廊接头内力初始阶段M-θ关系曲线呈凹面向下的变化规律，而随着弯矩M的逐渐增大，M-θ关系曲线曲率逐渐减小，最终M-θ关系曲线接近于一条近似的直线。从图3 中可以看出随着轴力的逐渐增大，M-θ关系曲线的初始斜率也逐渐增大。

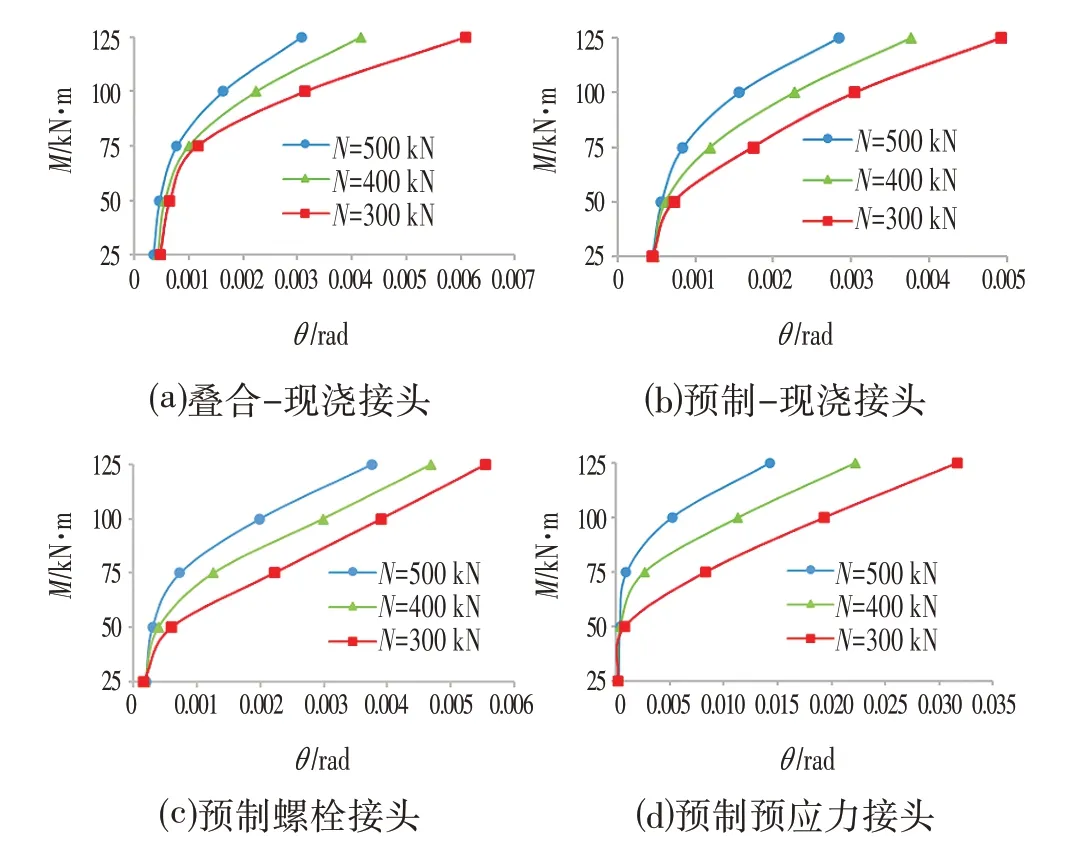
图3 4种典型接头不同内力组合接头M-θ 关系曲线Fig.3 The M-θ Curve of 4 Typical Joints

3 装配式综合管廊接头刚度的有限元计算

3.1 基本假定

在弹性范围内，对有限元模型作以下假定：①接头断面的转角和变形非常微小，属于小变形范畴；②除接头端面外，接头其余断面变形前后均为平截面；③接头材料为均质的各向同性材料。

3.2 建立计算模型

通过有限元分析软件ABAQUS 分别对4 种管廊接头的刚度进行了计算分析。初步计算时，以叠合-现浇接头为例，建立了两种计算模型，分别为模拟真实构造形式的L 型接头模型和简化后的直梁接头模型，如图4 所示，经过试算，同样计算工况两种模型的计算结果差异在15%以内，为避免大量的非线性接触导致不易收敛、计算时间过长，且本文主要针对接头拼缝的抗弯性能进行研究，故选定直梁接头模型作为接头有限元计算模型。

图4 接头有限元计算模型Fig.4 Finite Element Calculation Model of the Joint

模型中混凝土采用C3D8I 单元、钢筋采用T3D2单元分别建模，不考虑钢筋与混凝土之间的粘结滑移，新旧混凝土之间采用面与面接触。模型的加载参照单跨简支梁的受力模式，计算时通过在两端施加水平荷载P形成接头轴力N，通过施加竖向荷载Q形成接头弯矩M，如图5 所示。计算时采用3 级轴力N分别为500 kN、400 kN、300 kN，每级轴力对应5 级弯矩M分别为125 kN·m、100 kN·m、75 kN·m、50 kN·m 和25 kN·m。，定义接头内力偏心距e=M∕N，计算中忽略接头的自重影响。

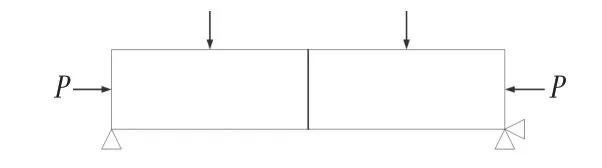
图5 管廊接头有限元计算模型加载示意图Fig.5 The Loading Model of Joint

3.3 计算结果

有限单元计算中，接头转角可通过接头断面边缘的节点A 和节点B 的位移推算而得，计算方法如图6所示。

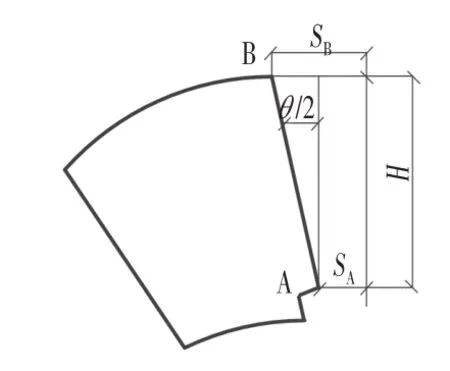
图6 接头转角计算示意图Fig.6 Calculation of Angle of the Joint

根据小变形假设，接头转角θ可按下式近似计算：

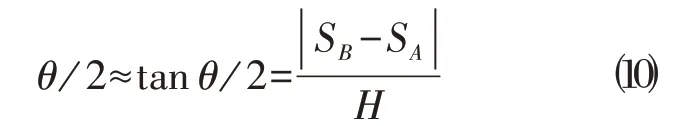
其中，SB为节点B 的水平位移；SA为节点A 的水平位移；H为接头断面的高度。根据式⑴可得，接头抗弯刚度值为：

4 种接头不同内力组合接头M-θ关系曲线如图7所示。

从图7中可以看出，在计算条件相同的前提下，有限元模型计算的M-θ曲线与力学解析模型的计算结果呈现了类似的变化规律，即轴力一定，M-θ曲线各点的切线斜率dM/dθ（接头抗弯刚度Kθ）随着弯矩M的增大而逐渐减小，并最终趋于稳定；随着轴力的逐渐增大，M-θ关系曲线的初始斜率也逐渐增大。出现这种现象的原因主要是在内力作用的初期由于接头弯矩非常小，管廊接头轴力对接头转动的约束能力非常强，随着接头弯矩的M的不断增大，管廊接头断面受力中性轴逐渐上移，接头发生挠曲，轴力的约束能力也在变形过程中逐渐降低，接头断面逐渐分离并形成受压区张开区，钢筋及螺栓受拉作用逐渐充分并和受压区混凝土共同协调作用以抵抗外部荷载，最终在复杂的力学环境中接头趋于稳定。

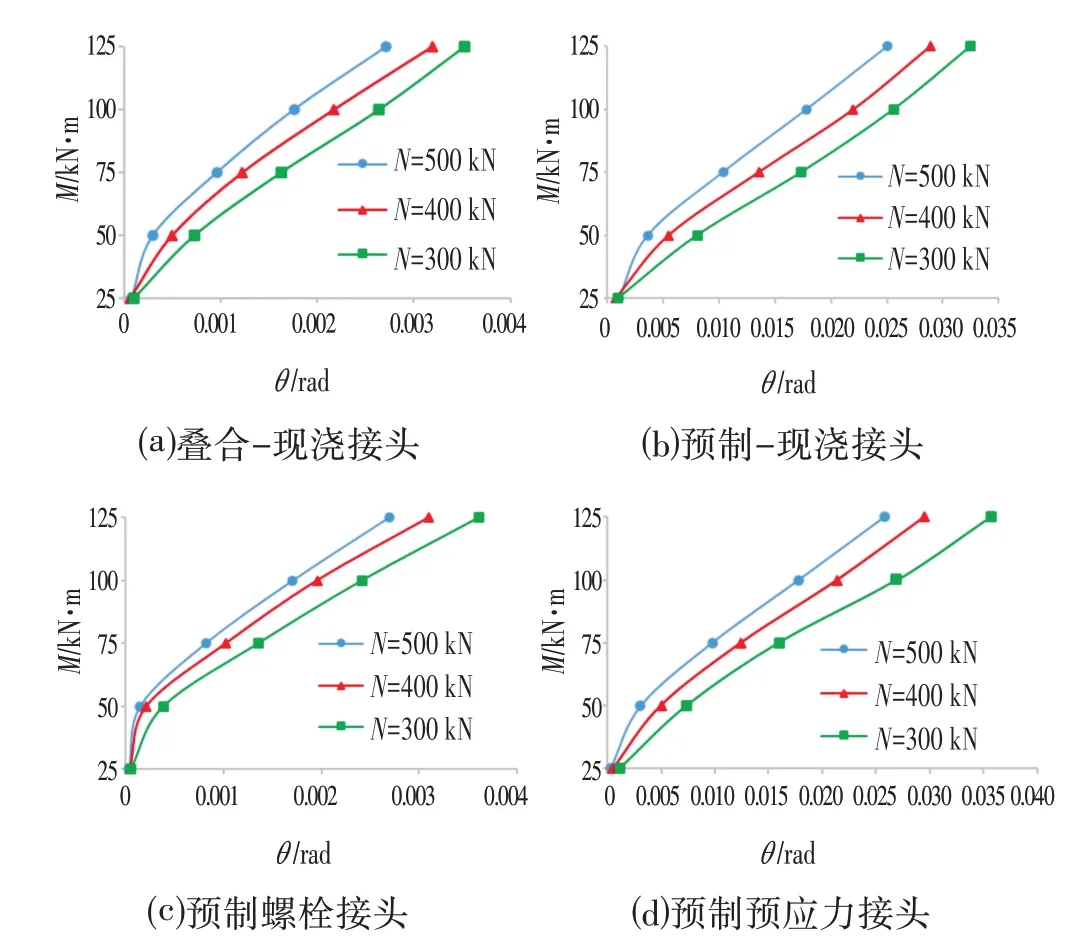
图7 接头不同内力组合接头M-θ 关系曲线Fig.7 The M-θ Curve of Different Combination of Internal Forces

3.4 两种模型计算结果对比

从图3 和图7 可以看出，两种计算模型基本上都正确的反应力管廊横向接头变形的总体规律，现以轴力N=400 kN 工况为例，对比分析力学解析模型与有限元模型之间的差异，叠合-现浇接头与预制螺栓接头的两种模型的M-θ曲线对比如图8所示。

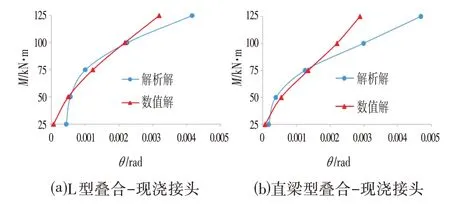
图8 现浇接头解析模型与有限模型M-θ 关系曲线对比（N=400 kN）Fig.8 Comparison of M-θ Curvse Between the Analytical Solution and Numerical Solution of the Joint

从图8 中可以看出，虽然两种接头模型呈现了类似的变化规律，但两种模型的计算结果存在一定差异，一方面，这是由于三维有限元模型在纵向的拓展一定程度上提高了接头的抗弯性能，而平面解析力学模型无法考虑接头部分对管廊接头力学性能影响的空间效益；另一方面，有限元模型接头应力分布形式与解析模型假设的三角形接触应力分布形式也存在一定的差异。综合看来，解析模型和有限元模型均能较好地反映管廊横向接头的力学性能变化规律。

4 结语

本文分别采用刚度解析法和有限元数值模拟，对装配式综合管廊的叠合-现浇、预制-现浇、预制螺栓和预制张拉4 种接头的抗弯刚度进行了计算，分析两种方法的计算结果可以发现：

解析模型和数值模型的计算结果存在一定差异，但都呈现了类似的变化规律，即当轴力一定，接头抗弯刚度Kθ随着弯矩M的增大而逐渐减小，并最终趋于稳定；随着轴力的逐渐增大，接头抗弯刚度Kθ也逐渐增大。综合看来，两种模型均能较好地反映管廊横向接头的力学性能变化规律。