地下水渗流对基坑工程稳定性影响研究进展
邓 忻
(广州地铁集团有限公司 广州 510335)
0 引言
在我国经济不断迅猛发展的同时,城市化建设正有条不紊地进行。随着大量人口涌入城市,缓解交通不便与用地紧张的问题迫使大量地下工程实施,许多高层建筑拔地而起。大中城市兴起的这些工程都伴随着基坑工程的出现,基坑工程的深度与难度一直在增加。因此,基坑稳定性成为了重中之重。在影响基坑稳定性的各类因素中,地下水渗流的破坏作用不可忽视。唐业清[1]通过对多项基坑事故的分析与统计,指出其中约21.4%的事故都是地下水渗流现象所引起。周洪波等人[2]分析了收集到的52 个城市轨道交通车站基坑事故案例,归纳了6种事故类型,渗透破坏位列第一。
引起地下水渗流问题的原因主要有:①基坑开挖深度不断加深;②该地区的地下水位高且丰富。例如,天津、上海、武汉等地区的地下水位较高。在这些地区进行基坑工程时,在基坑内外巨大水头差的作用下,发生地下水渗流,导致基坑开挖区域出现孔隙水压力变化。同时还有效应力的改变。渗流场和应力场的变化不仅影响围护结构侧压力的计算,甚至可能造成更严重的工程事故,从而影响整个基坑的稳定性[3-4]。
在开挖基坑施工过程中,与地下水有关的主要危害是基坑底部的管涌、流土和坑底管涌[5-6]。探究地下水渗流对基坑稳定性的不利影响,已经成为了目前关注度较广的课题[7-10]。
本文针对地下水渗流对基坑稳定性的不利影响进行研究,首先叙述渗透问题的基础-渗透理论的发展历史,以理论的不断革新来表明人们对渗透问题的不断参悟。随后将结合理论分析法与试验分析法各自的特点,阐述人们对地下水渗透影响基坑工程问题的研究进展。最后总结以上方法值得肯定的地方与不足,并提出以后发展的建议。
1 渗透理论发展
早在1856 年,法国工程师DARCY 通过持续的试验,得出了砂类土孔隙介质渗流能量损失与渗流速度的关系,这便是十分有名的DARCY 定律,作为最经典的理论之一,目前它仍作为运用最广泛的基本理论。1886 年,同在法国的DUPIT 根据DARCY 定律研究了地下水的一维稳定流动和水井的二维稳定运动。1901 年,奥地利的FORCHEIMER 研究了更复杂的地下水渗流问题,从而奠定了地下水稳定渗流理论的基础。稳定渗流理论不包括时间变量,只能用来描述地下水能够达到的暂时平衡状态,而不能反映地下水随时间变化的实际运动状态。这个时间段多以试验方法为主。
随着时代的进步,更精确的数学分析方法也被应用于渗流理论的研究。1904 年,法国人BOUSSINESQ提出了地下水不稳定流动的偏微分方程,该方程与一般热传导方程非常相似。此后,渗流的研究进入了以严格的定量分析数学方法为主要研究阶段的发展阶段。1935 年,THEIS[11]在MEINZER 的研究基础上,将求解热传导方程的技术应用于研究地下水运动规律的领域,开创了现代地下水运动理论的新时代。BOULTON[12]、HANTUSH[13]、NEUMAN[14]分别于1969年、1972年、1975年对不同条件下的地下水非稳态渗流运动进行了理论研究,推导出不同条件下地下水非稳态渗流运动的分析公式。在这一时期,主要采用分离变量法、积分变换法、保形图法、格林函数法、镜像法和Boltmann 变换等方法来研究均匀液体的各种渗流问题。随着基于计算机技术的数值模拟技术的发展,人们在地下水渗流问题上有了新的突破。在数值求解的早期阶段,主要采用有限差分法。1960年,CLOUGH在其计算结构分析论文中首次提出了有限元法。1965 年,ZIENKIEWICZ[15]将有限元方法引入地下水渗流领域。到目前为止,该方法在稳定渗流领域得到了广泛的应用,后世对他的评价也颇高[16]。DESAI 首次利用有限元法求解非稳定渗流,而NEUMAN[17]则解决了饱和与非饱和渗流问题。
理论的研究并未停止。DANG等人[18]基于DARCY定律,建立了泥浆水的渗流积分方程和微分方程,同时得到了差分公式。JEYISANKER[19]建立了粗粒主渗流分析模型,取代了传统的基于连续介质的渗流模型,并分析了影响水的瞬时渗流和稳态渗流的因素。黄延章等人[20]论述了低渗透性多孔介质中非线性渗流理论的几个问题,阐明了渗流流体的性质,指出了多孔介质对流体通过的选择性,并提出了新的非线性渗流方程。王世芳等人[21]建立了流体在分形多孔介质中渗流时的绝对渗透率及相对渗透率的分形渗透率模型。结果表明,绝对渗透率是最大和最小孔隙面积、分形维数、形状因子的函数。夏韦等人[22]分析了几种孔隙-裂隙-溶隙组合情况的多空隙介质渗流特性,推导出相应组合的等效渗透系数,给出了描述多空隙组合介质的一般表达式,讨论了影响各种空隙组合的主要因素。
随着有限元的应用,有关地下水渗流问题的研究越来越多。人们开始将孔隙水与土颗粒结合起来,不再单独思考其中一种的影响,渗流-压力耦合模型得以发展,使得结果更加符合实际。TERZAGHI[23]的一维固结理论与BIOT[24]的三维固结理论是基础,也最为经典。后续人们在它们的基础上衍生出来更多的发展,将在下文结合具体的方法进行列举。
2 渗流计算方法
渗流计算方法主要包括理论分析法和试验分析法[25-27],如图1所示。
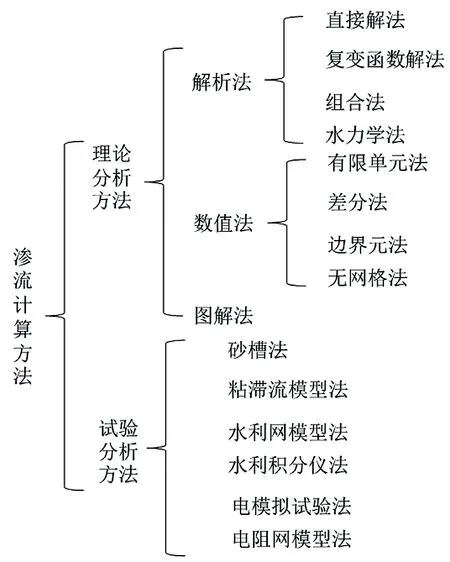
图1 渗流计算方法Fig.1 Seepage Calculation Method
2.1 理论分析法
理论分析方法可分为流体力学方法和水力学方法。流体力学方法是根据流体力学的基本原理和渗流边界条件来解决渗流问题的直接方法。它在理论上比较准确,但这种方法的计算很复杂。目前,它只能解决几个边界条件简单的渗流问题;水力法是一种基于渗流条件的一些假设基础上的方法。计算很简单。它只能得到渗流场中某一截面的平均渗流元素,而不能得到渗流场中任何一点的渗流元素。
就计算方法而言,理论分析方法可分为解析法、数值法和图形法。
2.1.1 解析法
渗流的基本微分方程作为一个数学和物理方程,解析法是对渗流问题的一种数学分析解决方案。该方法的核心是利用相关数学方法直接解决渗流的基本微分方程。解析法主要包括直接解法、复变函数法、组合法和水力法。
直接解法是一种直接解决渗流微分方程的方法。它需要在计算前对一些渗流条件进行近似的假设。复数函数法的核心是通过平面函数的变换,将待解的实际渗流区域转化为已有解的区域,这可以用保角变换理论来实现。组合法是将复杂的渗流区域按照具有理论解的渗流段或基本构件进行划分,从而解决整个地基的渗流场。在组合法中,根据渗流区的划分方法和解决问题的方法不同,主要分为基本构件法、阻力系数法和分段法。VERHOST 等人[28]采用直接解法研究了倾斜含水层的地下水渗流特征。根据稳定补给的连续性方程,假设含水层是均质和各向同性的,结合DARCY 定律确定了倾斜含水层的稳定补给的Boussinesq 方程。利用拉普拉斯变换及其逆变换和DARCY 定律得到基于坡度的水位高度和渗流,从而确定倾斜含水层有渗透补给时的地下水位线和渗流,然后进行排水设计。吴林高[29]考虑了抽水过程中土样高度和有效应力的变化对土壤渗透系数的影响,推导出地下水非稳态渗流的变参数数学模型。根据DARCY 线性渗透规律和线性回归拟合,通过抽水压实模拟试验和回注膨胀模拟试验测得的数据,得到渗透系数的变化规律。
2.1.2 数值法
数值方法种类繁多。应用有限差分法[30]来求解渗流自由面的研究工作相对较少。周念清等人[31]采用三维有限差分法对基坑降水对上海地铁11 号线徐家汇站进行模拟,数值模拟结果与地下水位实际监测数据十分吻合。边界元法[32-33]使解的维度减少,解的精度也相对较高,但推导和求解中的边界积分方程却非常复杂。所以这种途径暂时并未受到广泛的认可。无单元法是一种基于滑动最小二程法的有限元计算方法,用于理解渗流场。采用无单元法计算渗流场仅需知道计算域内的节点信息,节点可以随意分布,因此具有节点分布灵活和求解计算精度高的优点[34]。
应用最为广泛的还是有限元法。罗晓辉[35]对基坑的稳定和非稳定渗流进行了有限元分析,研究了渗流场。分析忽略了土体变形和孔隙压力耗散的耦合效应,将渗流场的水力作用与应力场耦合起来,得到了深层开挖过程与地下水渗流对基坑稳定性影响的基本规律。
姜忻良等人[36]采用三维有限元法分析了基坑中渗流场的分布特征,比较了不同土质条件下渗流对基坑土的渗流稳定性的影响。试验表明,在均匀的各向同性非层状土中,基坑转角和溢流点附近的水力梯度最大,整个基坑最容易发生渗流破坏的地方就在于此。在成层土情况下,水头等势线有向渗透系数小的土层聚集的趋势。
董诚等人[37]结合算例介绍了应用PLAXIS 有限元程序模拟降水条件下的深基坑开挖过程,并通过有限元强度折减法计算了基坑的整体稳定性安全系数。他们得到了基坑在三种工作条件下的整体稳定性安全系数:潜水位产生的水压、渗流计算产生的水压和基坑外的水位不降。其基坑整体稳定性系数差别较大。
陈兴贤等人[38]建立了TERZAGHI 一维固结理论和深基坑降水的三维变参数非稳态渗流与地面沉降的耦合模型,并采用有限元数值分析方法对模型进行求解。该模型可以准确模拟和预测松散沉积层中深基坑降水引起的地下水渗流场和地面沉降的变化特征,考虑土体孔隙度、渗透系数、储水率随地下水位下降发生的动态变化。
卢玉林等人[39]通过渗流与应力的耦合作用分析了两级边坡的三维应力场特点,随后运用有限元强度折减法探讨了渗流作用下的边坡稳定性及影响因素。结果表明耦合法的数值要高于不耦合法,与边坡实际变形更为接近。随着平台宽度,倾角的增加,两级边坡的滑动面由单一面向双滑面发展,滑动区域也将随倾角的增加而逐渐减小。
邓思源等人[40]对FLAC 3D 有限元软件内置的4 种渗流模型进行受力分析,通过对比和分析各工况下总应力和孔隙水压分布情况,得出了流体分担外荷载的比例与刚度系数和时间有关等结论。
严露[41]为了研究基坑开挖引起的地下水渗流对周边环境的影响,通过平面应变渗流耦合有限元法结合基坑支护形式和地下水控制措施对竖向位移、水平位移影响范围进行了分析。
2.1.3 图解法
图解法是一种通过绘制流网来近似求解渗流基本微分方程的方法。该方法主要是根据流网的特性,结合边界条件,通过试画方法逐步修正,得到渗流场的近似解。该方法具有简单、快速的优点,能够快速有效地解决均匀渗透介质和给定边界条件下的加压渗流问题。它往往结合前面的方法一起应用,使得结果更直观,更准确。
2.2 试验分析法
试验分析法[42]是一种将渗流形式和过程从室外搬到室内的物理实验方法。它不仅可以模拟用分析方法难以解决的复杂渗流问题,而且可以检验渗流过程中的基本原理和观察可能出现的现象。是一种极其重要的研究方法。只不过这些试验方法也有很多缺点。它们只能分析相对简单的渗流场,而且模拟模型和实际情况之间的一些因素会有所不同,使得计算结果会出现不同程度的误差。其中砂槽模型是应用较广泛的一种方法。
胡静[43]模拟软土地区二元结构地层,进行深基坑降水模型实验,观察地层承压地下水水流运动状态和运动规律,同时进行土样渗流试验,观测水压的变化,研究弱透水层承压水在降水过程中的“滞后和位差”现象和问题。
薛丽影等人[44]设计了符合基坑工程条件的模型试验系统,可以模拟基坑地下水渗流。通过给定进水箱与排水箱的水位可以实现基坑内外水头恒定,从而形成稳定的渗流。
刘丰敏等人[45]通过模型试验研究了层状含水层的渗流规律,并与不同计算方法的结果进行对比分析,发现弱透水层类型对层状含水层渗流场影响较大。此外,试验条件也影响了计算方法。当夹层分别是粉质粘土和粉砂时,试验结果分别与分层法计算结果和渗透系数加权平均法计算结果接近。
3 结论与展望
从19 世纪到现在,渗透理论的发展是值得肯定的。从一维固结理论到三维固结理论,从单体受力模型到渗透—应力耦合模型,可以看到理论趋于完善。结合计算机技术有限单元法,边界单元法等,实际应用的情况更可观。但是也要看到其中的不足。随着更多高层建筑与地下工程的建设,更具难度和深度的基坑会频繁出现,那时需要更好的理论与技术支持。
现在大量的渗流耦合模型都是针对某种区域的土质,且有不少限定条件的假设,几乎不具有较为全面的说服力,那么一个统一的标准便是研究的目标。为此,我们应该注意以下几点:
⑴ 成层土体将是深基坑降水必须要面对的问题。当地下水流经不同性质的土层时,土体的渗透系数将不再是定值或者单一的,那么这种情况的渗透系数与土的变形关系值得深思。
⑵在降水渗透的过程中,土体会因为二次固结而强度发生变化,那么渗流耦合模型中需要考虑土体强度随渗透参数与时间因素的关系。
⑶在降水渗透的过程中,土体因为固结孔隙比会减小,空隙分布状态会发生变化,各向异性使得一系列参数变得复杂,所以选择好正确的本构模型十分重要。
⑷目前大量的试验分析和数值法都是针对稳定流的渗流问题出发,而现实情况往往难以控制渗透情况,因此非稳定流的研究也极其需要。

