水压式垂直发射装置内弹道建模与分析

程李东， 姜毅， 张曼曼， 王文杰

(北京理工大学 宇航学院， 北京 100081)

潜艇作为水下武器的移动发射平台，具有隐蔽性好、机动性强、作战效能高、载弹量和威慑力大、续航时间长等特点[1-2]。潜艇的主要攻击手段为鱼雷和导弹，其中潜射导弹主要包含巡航导弹[1]、弹道导弹[3]和防空导弹[4]等。按发射时导弹的初始姿态可将发射方式分为水平发射、倾斜发射和垂直发射。垂直发射具有诸多优点，如潜艇能储存更多数量和种类的导弹，作战时不受潜艇航向和导弹发射角的限制，可进行全方位、多目标攻击，导弹出水快、稳定性好，以及弹道简单、抗海浪干扰能力强等[5]，这些使得垂直发射成为未来潜射导弹发射技术的主要发展方向[2]。

现阶段各国主流的潜射导弹垂直发射方式按动力源可分为筒内注水热发射、压缩空气弹射、燃气弹射和燃气-蒸汽弹射[6]，这些发射方式在发射过程中都会从发射筒内溢出大量气体，产生较强的红外或噪声信号，削弱潜艇的隐蔽性[5]，从而在一定程度上威胁潜艇的安全。近年来，水压式发射技术在鱼雷发射上逐渐得到应用和推广，其基本原理是将其他形式的能量，如电能或压缩气体的内能等，转化为发射管中水的液压能，再转化为鱼雷的动能和克服鱼雷阻力做功[7-14]。这类发射方式不向艇外排放任何的气体，具有低发射噪声，无舱室增压等优点[15-16]。

本文研究一类水压式潜射导弹垂直发射装置的内弹道过程，建立该类发射装置的准一维内弹道模型。将该模型的计算结果与商用计算流体力学(computational fluid dynamics, CFD)软件的数值仿真结果对比，初步验证了模型的有效性。在内弹道模型中，针对潜射导弹或鱼雷发射装置的弹筒间隙泄流问题提出了一种新的计算方法。与CFD仿真的结果对比可知，本文计算方法比已有文献中的方法更精确。

1 准一维弹射内弹道模型

1.1 发射装置工作原理

水压式潜射导弹发射装置的原理图如图1所示，导弹贮存在内筒内，内筒与外筒构成同心圆环，其间放入活塞。图中的Ⅰ区为内外筒之间活塞以下的区域，Ⅱ区为内筒内部弹底以下的区域，Ⅲ区为潜艇所在海域，Ⅳ区为内外筒之间活塞以上区域。发射之前进行均压开盖注水，使Ⅰ区和Ⅱ区以及弹筒间隙内都充满海水，与Ⅲ区联通。发射时动力装置推动活塞向下运动，在水压的作用下导弹向上加速出筒。

图1 水压式垂直发射装置原理Fig.1 Schematic of hydraulic submersible vertical missile launcher

出于讨论的一般性，原理图中没有给出动力装置，可以采用压缩空气驱动、液压驱动、电机驱动或电磁力驱动等作为动力来源。此外，若将Ⅳ区与Ⅲ区联通起来，则构成水压平衡式发射装置，其设计和使用可以不依赖于发射深度[8]。本文研究中不区分动力源和Ⅲ区与Ⅳ区是否联通，而是关注这类发射装置的筒内及弹筒间隙内的流动与弹体运动的内弹道问题。

1.2 基本假设

本文基于以下基本假设建立水压式垂直发射装置的内弹道模型：

1)发射过程为绝热过程，发射装置与外界无热交换[19]；

2)初始时刻无任何流动，水压与重力达到平衡；

3)海水具有弱可压缩性，但不考虑发射过程海水的温度变化，其压强-密度遵循规律[17]：

式中：p为海水绝对压强；ρ为海水密度；E为海水体积模量。

4)不考虑发射过程中海水的空化效应；

5)Ⅲ区发射筒筒口附近的海水压强均匀恒定，依赖于发射深度；

6)弹筒间隙内的流动为层流，流动参数沿轴向和周向均匀分布，只沿径向变化[22]；

7)只考虑导弹在单方向的平移运动，不考虑偏移和转动。

1.3 内弹道建模

坐标系规定如图1所示，以筒底为坐标原点，向上为z轴正方向。

1.3.1 弹体动力学方程

根据牛顿第二定律可得弹体动力学方程：

(1)

式中：Mm、u、Am分别为弹体质量、速度和横截面积；pmb、pmt分别为弹体底面和头部的海水静压；Fmf为筒弹间隙流动造成的摩擦力；g为当地重力加速度。其中，

式中：h为筒口距离海面的高度；S为弹体位移；p0为海面气压；Cd为以Am为参考面积的弹体阻力系数。

1.3.2 弹筒间隙流动方程

基于假设6建立弹壁指向内筒内壁的一维坐标系如图2所示。

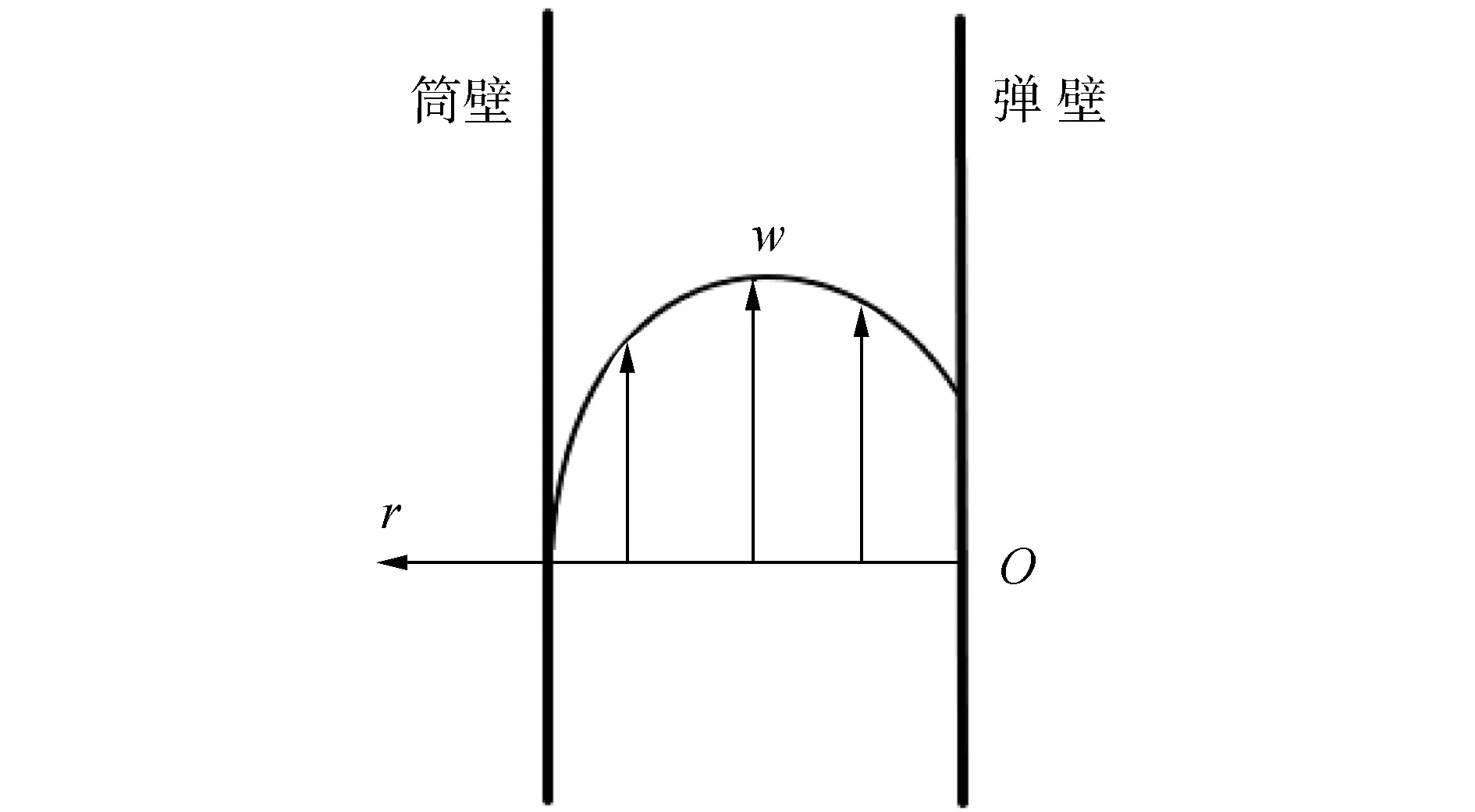
图2 弹筒间隙坐标系Fig.2 Coordinate system of cartridge gap

图2中曲线为筒弹间隙内的流速分布，间隙宽度为δ，弹体直径为dm，长度为Lm。由于，

δ≪πdm,δ≪Lm

弹筒间隙内的流动可近似为平行平板间隙流动[22]，因此满足动量方程：

(2)

式中：w(t,r)为间隙内海水流速；μ为海水动力粘度。基于假设6有：

式中：l为弹筒间隙长度；ph为基于假设5的发射筒筒口压强：

ph=p0+ρgh

式中：pz为弹筒间隙下端面的压强，考虑由Ⅱ区进入间隙的局部阻力损失，有：

pz=pmb-ρghm

式中hm为局部水头损失：

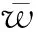
ξm=1.0

间隙内海水的质量秒流量为：

从而得：

式(1)中的弹体摩擦力为：

1.3.3 筒内流动方程

将 Ⅰ 区和 Ⅱ 区近似为圆管流动，粗估参数量级以计算雷诺数，取dm～0.5 m,u～10 m/s,ρ～103kg/m3,μ～10-3Pa·s，则

因此，筒内流动必须考虑湍流效应。Ⅰ区与Ⅱ区流动的伯努利方程为：

(3)

式中：pⅠ、pⅡ为Ⅰ区和Ⅱ区的平均压强，取活塞和弹体高度的一半位置的压强；zpst、zm为活塞下表面和弹底坐标；a=1.05为圆管湍流动能修正系数[22]；v为活塞运动速度；vin为内筒内海水流速；hf为阻力损失。其中：

式中：Ain为内筒截面积；Apst为活塞底面积；阻力系数ξf=ξf1+ξf2，ξf1为筒底的局部阻力系数，ξf2为沿程阻力系数：

文献[22]取ξf1=1.5，初步估计发射筒粗糙度Δ～0.05 mm，则：

初步估计参数量级，取管道长度lH～5 m，水力直径dH～0.5 m，则：

ξf2～0.1≪ξf1

因此，在整个发射过程中取ξf=1.6。

1.3.4 整体质量守恒方程

由Ⅰ区Ⅱ区和间隙内流动质量守恒可得：

dmⅠ+dmⅡ+Qdt=0

(4)

式中mⅠ、mⅡ分别为Ⅰ区和Ⅱ区的海水总质量。依据假设3有：

(5)

将式(5)代入式(4)可得：

(6)

式中VⅠ、VⅡ分别为Ⅰ区和Ⅱ区体积。

1.3.5 活塞动力学方程

由牛顿第二定律得活塞动力学方程：

Mpstapst=∑Fpst

(7)

式中：右端项为活塞所受合外力，包含驱动力、摩擦力和上下表面流体压力；Mpst为活塞质量；apst=dv/dt为活塞运动加速度。

1.3.6 运动学方程

弹体和活塞相关运动学方程为：

(8)

1.3.7 几何关系方程

弹体和活塞运动与区域Ⅰ/Ⅱ体积的几何关系为：

VⅠ=Apstzpst,VⅡ=Ainzm

(9)

综合上述，由式(1)～(3)和式(6)～(9)构成了水压式垂直发射装置的内弹道方程组。其求解可基于欧拉法或龙格库塔法等[23]，其中式(2)为偏微分方程，可采用有限差分法离散[24]。

2 模型验证

为验证内弹道模型的有效性，选择典型的发射装置参数建立CFD模型，基于有限体积法和一维刚体运动方程求解发射流场和弹体的运动[11,15,25]，并与同一参数下内弹道方程的解作对比分析。本文基于欧拉法求解内弹道方程，应用分层动网格方法求解CFD模型[11]。

不失一般性，本文研究中发射的驱动参数为活塞的加速度apst，各工况的活塞加速度如表1所示。其余关键参数有ρ=998.2 kg/m3，h=30 m，dm=0.5 m，Lm=6.75 m，δ=0.01 m，Apst=1.273 2 m2。

表1 各工况活塞加速度Table 1 Accelerations of each case

2.1 CFD模型与网格无关性

本文所用轴对称CFD模型图3所示，湍流模型为RNG模型，海水为弱可压缩液体模型(compressible-liquid)[26]。动量和压强采用二阶格式离散，其余变量为一阶迎风格式。

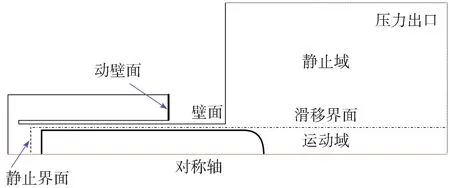
图3 计算流体力学模型Fig.3 The CFD model

对该模型其进行网格无关性分析，网格1～3的单元数量分别为8.14万、16.36万和21.40万。发射参数为工况 2，计算所得弹底压强、弹筒间隙流量和弹体速度曲线如图4所示。

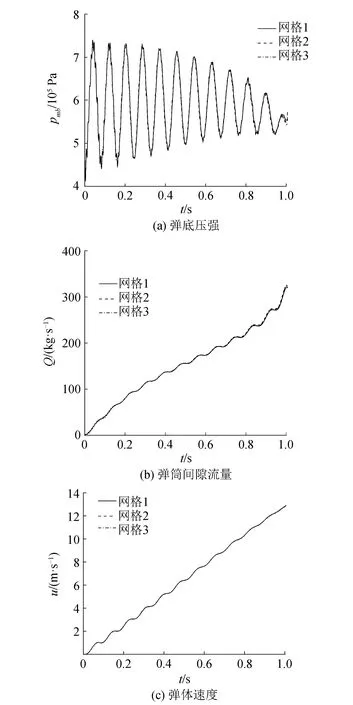
图4 网格无关性验证Fig.4 Verification of mesh independence

可见网格1～3的计算结果没有明显差异，因此可认为网格2已达到计算与网格无关，后续的计算皆采用网格2。

针对内弹道模型中弹筒间隙内流的式(2)的离散求解进行网格无关性分析，将间隙宽度分为10、30、50、70等分，发射参数仍与工况2相同，计算所得间隙流量曲线如图5所示。

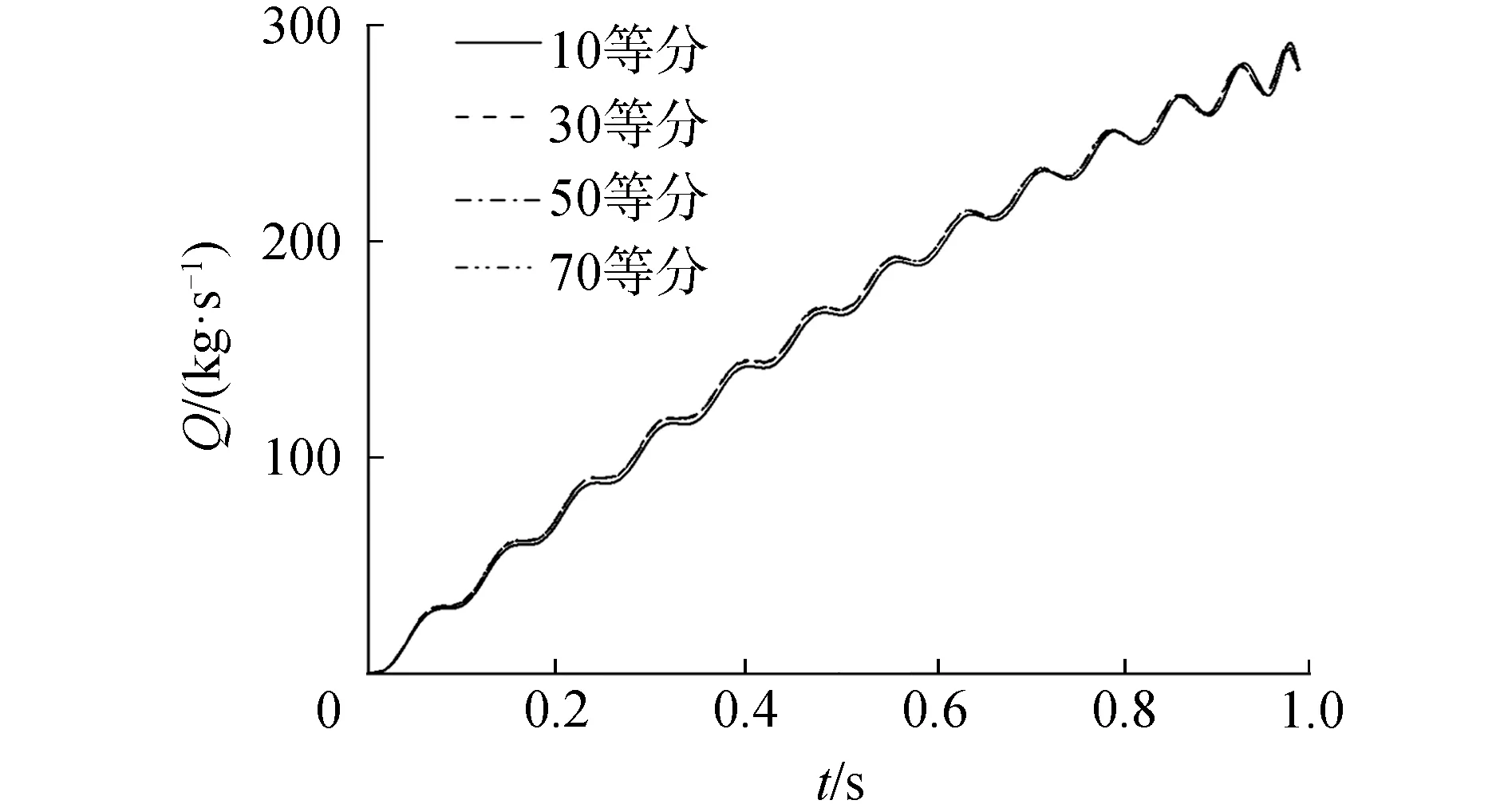
图5 弹筒间隙流量Fig.5 Mass flow rate in the gap

可见只有10等分网格的计算结果与其他3个结果有细微差别，因此可认为50等分已达到计算与网格无关，后续计算中弹筒间隙采用50等分。

2.2 筒间隙泄流

在质量守恒的约束下，弹筒间隙内的泄流流量直接关系到导弹出筒的速度。对于间隙流量的计算，已有的文献[17-21]中均基于平衡流动假设，建立流量与间隙两端压强和弹体速度之间的关系：

(10)

本文问题中，导弹发射过程仅仅约耗时约1 s，筒内压强高出筒口压强数倍且在不断变化，间隙内的流动很难达到平衡，直接应用平衡流动假设将导致缝隙流量剧烈震荡而使计算发散。因此，本文内弹道模型基于假设6)直接离散求解动量方程得间隙内流速分布进而求得流量。图6是CFD、本文方法和平衡流动假设所得工况2间隙泄流流量曲线。这里基于平衡流动假设的结果是将式(10)应用于本文模型所得压强和速度所得的流量曲线。

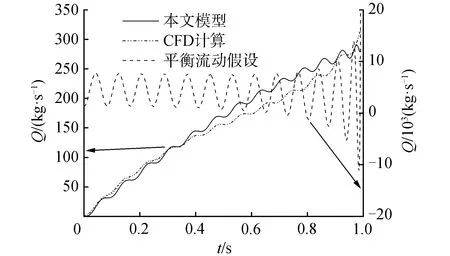
图6 各模型所得弹筒间隙流量曲线Fig.6 Mass flow rate in the gap by different models

由图6可见本文模型所得结果与CFD结果吻合较好，发射过程泄流总质量分别为158.9 kg和155.7 kg，相差2.05%。但根据平衡流动假设所得流量比前两者高出2个量级且大幅振荡，说明在本文研究的导弹发射过程中，平衡流动假设不再适用。同时表明，本文基于假设6)离散求解动量方程的方法是有效的。

2.3 弹底压强

对工况1～3分别采用本文模型和CFD方法求解，得到的弹底压强随时间变化的曲线如图7所示。

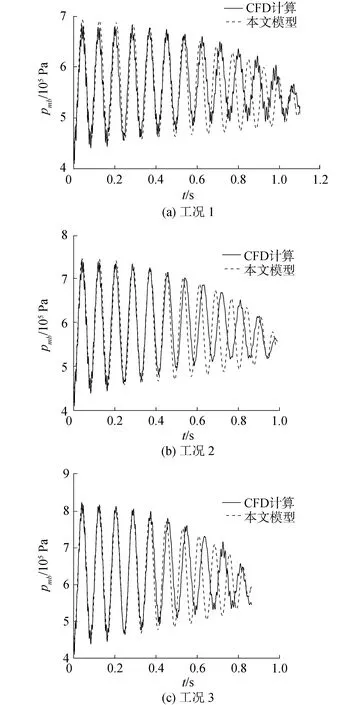
图7 各工况的弹底压强曲线Fig.7 Pressure on missile bottom of each case

由于水具有弱可压缩性，在不断匀加速运动的活塞作用下，压力波会在筒内往复传播。各工况下本文模型的压强计算结果与CFD的仿真相比，振幅和周期都吻合良好，证明本文模型在捕捉弹底压强动态变化方面表现良好。后期两者在相位上的差异主要由于CFD计算考虑了粘性和湍流效应导致。

2.4 弹底运动

对工况1～3分别采用本文模型和CFD方法求解，得到的弹体速度随时间变化的曲线如图8。由图可见本文模型在各工况下计算所得速度与CFD结果都很接近。出筒速度及相对偏差见表2，各工况的速度相对偏差都在3%左右，这表明本文模型在弹体出筒速度的计算上也表现良好。

图8 各工况弹体速度曲线Fig.8 Velocity of missiles

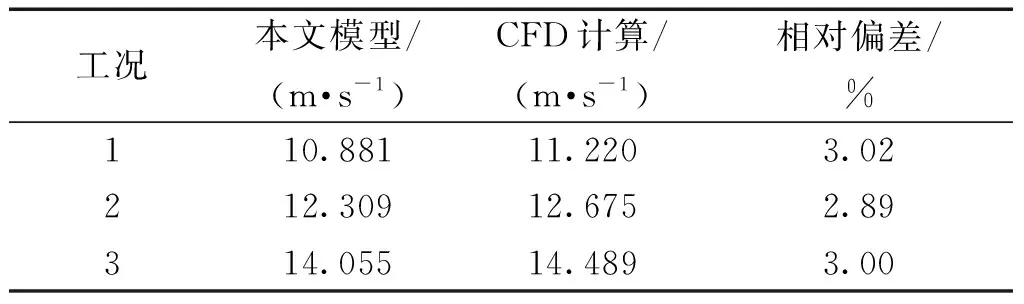
表2 各工况出筒速度及相对偏差Table 2 Outlet velocities and deviations

3 结论

1)相比于基于平衡流动假设的式(10)，基于一维流动假设和动量方程的式(2)更适合于求解两端压差较大的瞬态环形缝隙流动。

2)在本文发射参数下，本文提出的内弹道模型在弹筒间隙流量、弹底压强和弹体速度上都与CFD计算吻合良好，总流量偏差约为2.05%，出筒速度偏差约为3.0%，表明本文内弹道模型是有效的。

3)本文提出的环缝流动计算方法和内弹道模型可为相关理论问题的研究及工程设计提供参考。