苹果产量集成预测模型研究

张帆 王耐寒 兰鹏 王云露 陈国恩 周忠昌 孙丰刚

摘要：苹果产量与气象因素密切相关，建立以气象因子为变量的预测模型是实现产量预测的重要手段。单一预测模型受限于年际及空间变化，预测效果不佳。选取山东省4个苹果主产县，通过对2005—2019年气象数据和苹果产量数据进行分析，构建苹果产量集成预测模型。首先，通过趋势分析法将苹果产量分解为趋势产量和气象产量。其次，分别针对月平均气象数据，依据距离相关系数筛选影响产量的关键气象因子。最后，以支持向量机回归、多元线性回归和决策树回归为基础模型形成集成预测模型。结果表明，集成预测模型精度优于单一模型，其平均相对误差在3.0%～4.5%，均方根误差在1.5～2.6。该模型在不同地区均表现出较好的预测效果，可为苹果产量预测提供理论支撑。

关键词：苹果产量;气象因子;距离相关系数;集成预测模型;产量预测

中图分类号： S162.5文献标志码： A

文章编号：1002-1302（2022）04-0181-06

收稿日期：2021-04-21

基金项目：山东省重大科技创新工程（编号：2019JZZY010706）;山东省重点研发计划（编号：2017CXGC0206、2019GNC106106）;山东省自然科学基金面上项目（编号：ZR2019MF026）。

作者简介：张 帆（1997—），男，山东潍坊人，硕士研究生，从事农业数据分析研究。E-mail：18265651358@163.com。

通信作者：孙丰刚，博士，副教授，从事农业信息化领域研究。E-mail：sunfg@sdau.edu.cn。

水果是人体补充维生素和矿物质的重要来源，苹果因其独特口感和丰富的营养深受人们喜爱。据统计，2018年我国苹果产量为3 923.3万t，占世界苹果总产量的43%;消费量为2 720万t，占世界苹果消费量的48%。我国已成为世界最大的苹果生产国和消费国，果树产业发展过程中要结合大数据的采集、分析和市场状況，加强顶层设计[1]。苹果产量常因气象变化产生较大波动，因此依据气象数据对产量进行精准预测，成为辅助苹果生产决策的有效手段。

在现有研究中，常将总产量分为趋势产量与气候产量两部分，其中趋势产量受一段时间内社会技术发展水平影响，其年际变化具有相对稳定性;而气候产量受气象要素为主的短周期变化因子（农业气象灾害为主）影响，其年际变化较大。通常利用滑动平均法、多项式法、线性拟合和“S”形曲线拟合等方法来分离趋势产量与气候产量[2-4]。年际间的气候产量受气象因素影响较大，一定范围内，产量与降水量及日照时数呈负相关，与气温呈正相关[5]。在全球变暖背景下，苹果春季物候期呈提前趋势、秋季物候期呈延后趋势，极端气象条件影响产量可能性增大[6-8]。预测气候产量时常用灰色关联法来分析气象数据对作物产量的影响，后将关键气象因子作为预测变量，采用诸如多元线性回归等方法对总产量进行预测[9-12]。单一预测模型随年际变化波动较大，难以满足当今对数据精度的要求，因此本研究考虑采用组合预测模型对苹果产量进行预测。

由于苹果产量随年际、地域空间变化表现出较大差异，单一预测模型往往只能在气象与产量变化特征相似地区取得较好效果。本研究选取支持向量机回归（support vector machine regression，简称SVR）、多元线性回归（multiple linear regression，简称MLR）、决策树回归（decision tree regression，简称DTR）3种方法作为基础模型，集成这3种方法的预测结果作为最终结果。首先，基于距离相关系数来实现特征选择，选取相关性高的变量;其次，为丰富数据集，采用循环预测法，顺序选取1年为测试集，其余年份数据为训练集，搭建预测模型，并根据误差情况确定每个模型的预测权重，最终实现集成预测。为验证模型的稳定性，本研究选取山东省4个地区苹果主产区作为研究对象，对集成预测模型进行验证，表明所提集成预测模型具有良好的预测效果。

1 数据来源与研究方法

1.1 研究区域概况

山东省是我国苹果产业大省和环渤海湾优势苹果主产区的典型代表，地处34°N～38°N，属温带季风性气候，雨热同期，光照充足，果实成熟期昼夜温差大，苹果种植条件得天独厚。至2020年，山东省苹果种植面积、总产量、苹果品质等均居国内领先地位，苹果产业已成为山东省重要产业和特色名片。山东省苹果主产区由鲁西、鲁中不断向胶东半岛迁移，以胶东半岛为中心的苹果种植新格局已经形成[13]（图1）。本研究基于山东省主产区分布空间特点，选取栖霞市、莱西市、沂源县、单县为研究对象，涵盖东部丘陵、中部山区、西南部平原。

1.2 数据来源

本研究使用的数据资料包括上述气象观测站的气象数据和4地苹果园种植面积、总产量等数据。气象数据包括2005年1月1日至2019年12月31日的逐日实测数据，选用日照时数（h）、温度（℃）、降水量（mm）3类典型气象因素，其中日照时数、降水量为当日累计值，气温为当日平均值。产量资料通过各地统计年鉴获得，包括苹果园种植面积和总产量。利用产量资料获得产量（t/hm2）来分离趋势产量与气候产量。

1.3 研究方法

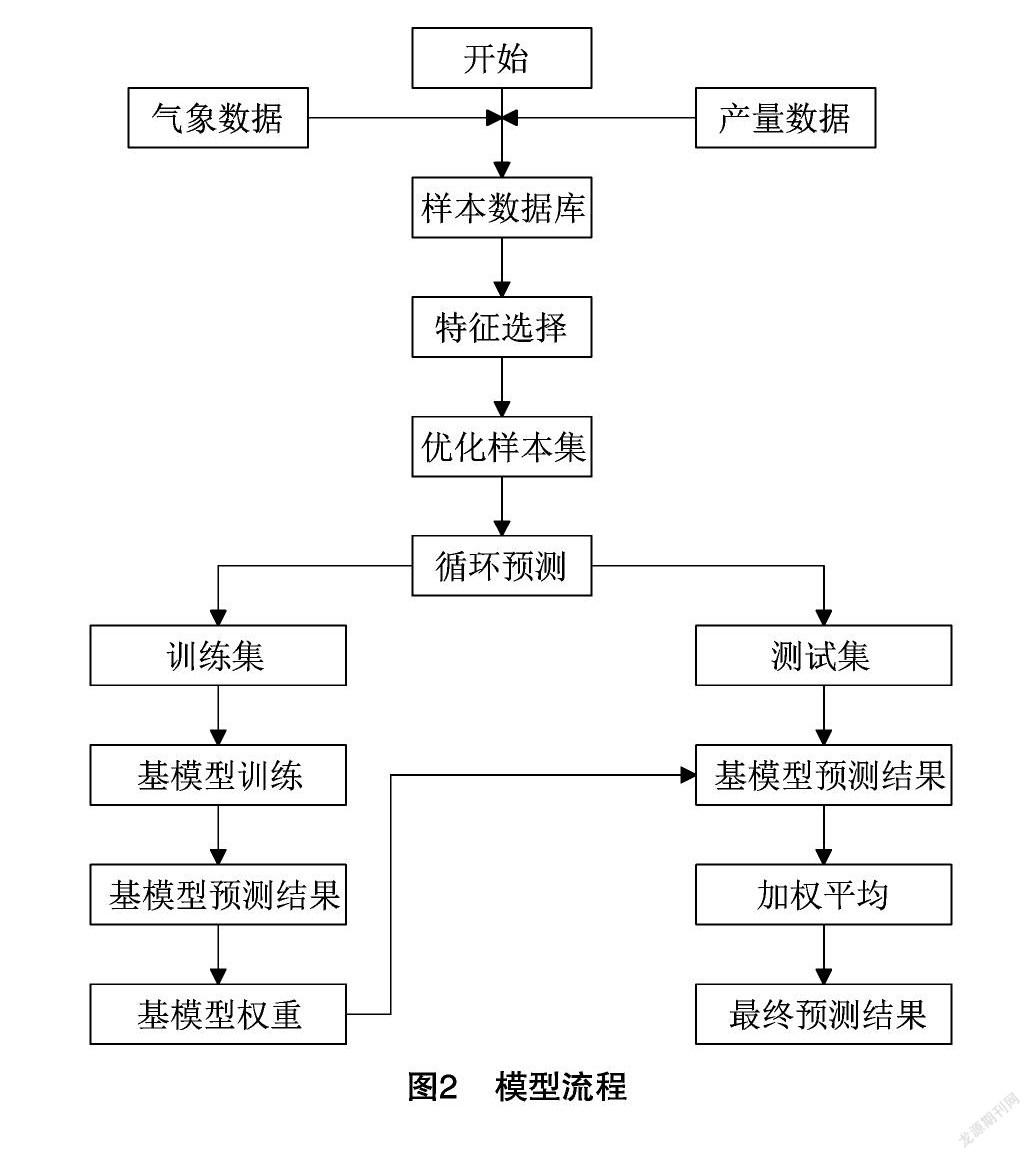
由于不同苹果主产区地理地貌差异性大，影响因素不同，单一模型预测效果常存在较大波动。本研究建立基于集成学习的预测模型，流程见图2，主要思路为通过分析历史气象因子对苹果产量的影响，筛选出关键气象因子建立预测模型，并通过待预测年的关键气象因子对当年产量进行预测，最后利用循环预测对各模型预测效果进行验证。

本研究方法可分为如下步骤：

（1）利用气候产量与3类气象因子建立样本数据库。

（2）依据距离相关系数，从样本数据库中挑选预测变量作为优化后的样本集。

（3）从2005—2019年中顺序选取1年为测试集，其他年份数据作为训练集。利用训练集数据训练支持向量机回归、多元线性回归和决策树回归模型，得模型参数与训练集预测结果。

（4）将循环预测结果与对应真实值求相对误差，确定模型权重，使用加权平均法进行集成预测，得最终预测结果。

1.3.1 数据预处理

影响苹果产量的因素可分为自然因素和人为因素。自然因素包括气象因素、土壤因素和品种因素等;人为因素可包括种植养护技术、农业化工技术和农业机械技术等。某一地区苹果种植之后，土壤因素和品种因素在之后一段时间内将保持相对稳定状态，因此本研究对苹果产量预测时只涵盖气象因素和人为因素。

人为因素对苹果产量的影响相对平缓，因此使用趋势产量拟合法表示人为因素带来的产量变动，并对气候产量进行预测，进一步计算后得产量预测值。趋势产量与产量的关系如式（1）所示：

Y产量=Y趋势产量+Y气候产量。（1）

为了保证在尽量多的使用已有天气数据的同时所选用预测变量的个数适宜，本研究对天气数据以月为单位进行均值化处理。同时，为避免量纲对

预测结果的影响，采用min-max标准化方法对样本气象数据进行标准化处理，标准化公式为：

yi=xi-xminxmax-xmin。（2）

1.3.2 变量筛选

建模过程中，变量过多会造成模型复杂，拟合速度慢。另外，无关或相关性弱的变量加入会造成相关性强的变量显著性降低，降低模型的可解释性。因此，本研究选用距离相关系数对变量进行评估。与皮尔森相关系数和秩相关系数相比，距离相关系数在可以衡量非线性相关关系的同时，有更好的检验功效[14]。

设{（ui，vi），i=，…，n}是总体（u，v）的随机样本，则距离相关系数可用如下公式[13]计算：

d^corr（u，v）=d^cov（u·v）d^cov（u·u）d^cov（v·v）。（3）

其中 d^cov2（u，v）=s^1+s^2-2s^3，S^1、S^2、S^3分别为：

S^1=1n2∑ni=1∑nj=1‖ui-uj‖du‖vi-vj‖dv

S^2=1n2∑ni=1∑nj=1‖ui-uj‖di1n2∑ni=1∑nj=1‖vi-dj‖dv

S^3=1n3∑ni=1∑nj=1∑nl=1‖ui-ul‖du‖vj-vl‖dv。（4）

1.3.3 集成预测

由于单一预测模型对不同地区、不同年份预测结果误差差异较大，本研究使用加权平均法对3种基模型预测结果进行集成。此方法依据模型在测试集中的表现确定基模型权值，减小了在训练集中表现较差的模型影响最终预测结果的程度，模型权重计算公式[15]如下所示：

wj=S-1j∑mj=1S-1j。（5）

式中：wj表示第j个模型的权重;Sj表示第j个模型的平均相对误差的绝对值;m表示模型的数量。本研究使用的基础模型包括以下3种。

1.3.3.1 多元线性回归

设y为因变量，x1，x2，…，xk为自变量，则多元线性回归模型可表示为：

y=b0+b1x1+…+bkxk+e。（6）

式中：b0为常数项;b1，b2，…，bk为回归系数;e为误差项。式（6）改写为矩阵形式可得：

y1y2.ym=b0+b1

x11x12.x1m+…+bn

xn1xn2.xnm。（7）

即Y=XB，则参数B求解公式如下所示：

B=（XTX）-1XTY。（8）

1.3.3.2 决策树回归

决策树回归通过分析对象属性与对象值之间的映射关系，将特征空间进行划分，每个叶子节点代表每个特征空间区域都有特定的输出。对于给定训练集，设第j个变量和它的取值s作为切分变量和切分点，假设最终划分为M个区域，则决策树回归模型[16]可表示为：

f（x）=∑Mm=1c^mI，x∈Rm。（9）

其中，當x∈Rm时I为1，否则I为0。结果如式（10）所示：

R1（j，s）={x|x（j）≤s}

R2（j，s）={x|x（j）>s}

c^m=1Nm∑xi∈Rm（j，s）yi，x∈Rm，m=。（10）

1.3.3.3 支持向量机回归

支持向量机回归在支持向量机基础上引入不敏感损失函数，拟合回归模型，使得f（x）与真实值y相差最小，支持向量机回归可形式化[17]为：

f（x）=∑mi=1（α^i-αi）k（xi，x）+b。（11）

其中：αi与α^i为非负拉格朗日乘子;k（xi，x）为核函数，本研究中使用如下核函数[式（12）]并进行网格化

k（xi，x）=xi·x线性

[（xi·x）+1]·d多项式

exp（-g‖xi-x‖2），g>0径向基。

（12）

2 结果与分析

2.1 数据预处理结果

由于趋势产量具有相对的稳定性，而气候产量受气象条件影响明显，为准确筛选关键气象因子，需要先将趋势产量和气候产量进行分离。常用的趋势产量拟合方法有线性拟合、滑动平均、多项式拟合、“S”形函数拟合等。各地区因地理环境、品种等差异，年际产量表现出不同特点，如本研究中栖霞市单产表现出近似线性增长的趋势，而沂源县单产量则表现为先增长后保持相对稳定的“S”形变化趋势，因此需结合不同地区的变化特征选择适当方法来获取趋势产量。图3中以栖霞和沂源为例给出了趋势产量的拟合公式及实际产量、趋势产量。

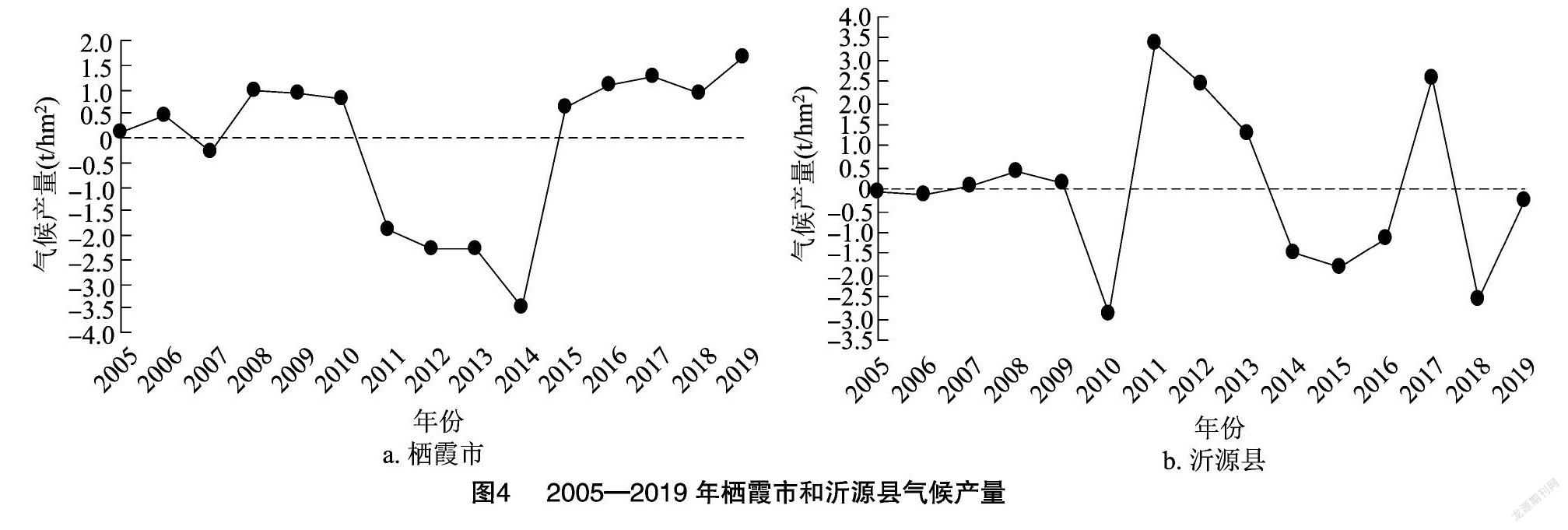
依据“公式（1）”及图3中趋势产量拟合公式，计算得气候产量见图4。

2.2 变量筛选结果分析

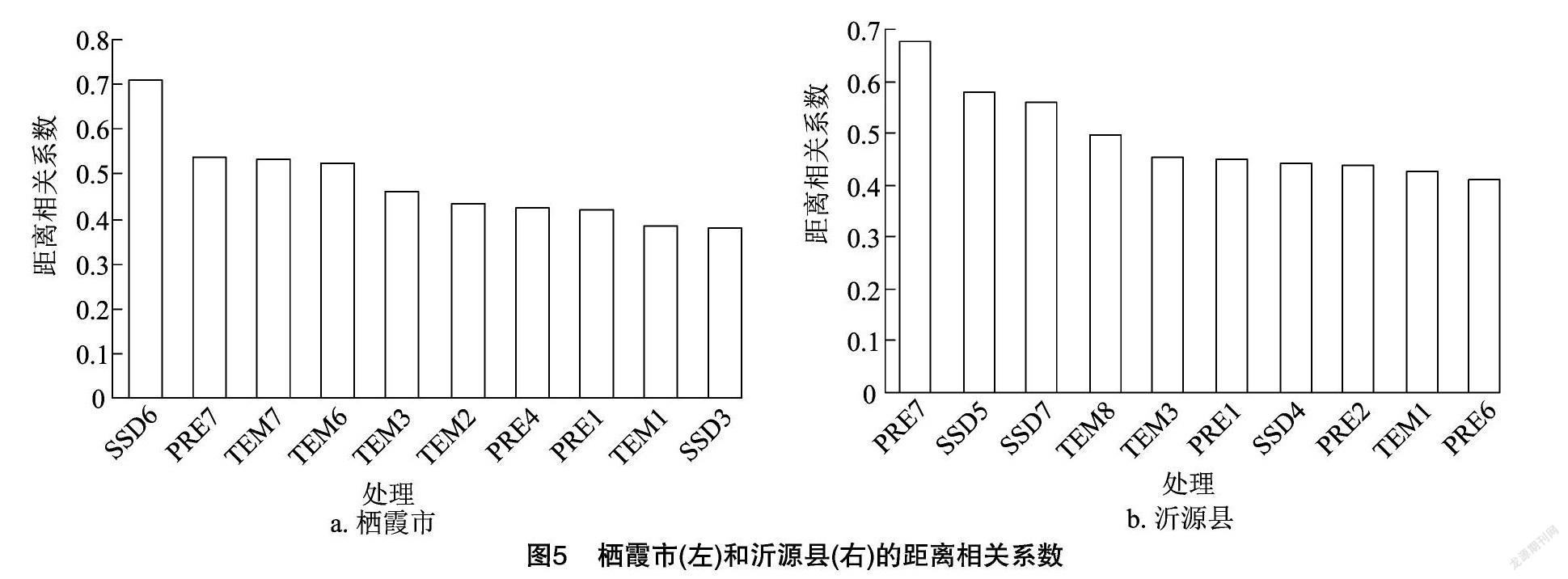
本研究利用标准化后月平均气象数据与图3中气候产量，依据“公式（3）”求解距离相关系数，部分变量的距离相关系数结果见图5，其中PRE表示降水量、TEM表示气温、SSD表示日照时数，后缀数字表示月份，如“SSD6”表示“6月平均日照时数”。

为突出关键气象因子，提高模型运行速度，预测变量选取时，设置变量数量阈值计算函数[14]如式（13）所示。

n=Nlg N4/5。（13）

其中：n为变量数量阈值，N为变量总数。

结合图4可以得出，筛选出的预测变量集中在5—7月平均光照、3月及6—8月平均气温、7月平均降水量。3月为影响果树开花的关键时期，同时也是春季冻害高发时期，苹果树要求日平均温度达5 ℃ 以上，且经过10～15 d才能萌芽，气温同时为影响花期的主要气象因素。6月为苹果树花芽分化期和果实膨大期，20～27 ℃的日平均气温和大于 10 ℃ 的日温差有利于花芽分化。7—8月为果实膨大期，此时段需要充足的降水以及适宜的温度：土壤含水量达到最大含水量70%，平均气温在20～27 ℃ 之间，日温差在10 ℃以上。

综上所述，通过距离相关系数所筛选变量与基于经验和物候期筛选变量相吻合，有较强的解释性，筛选结果符合预期，可用于建模预测。

2.3 预测结果分析

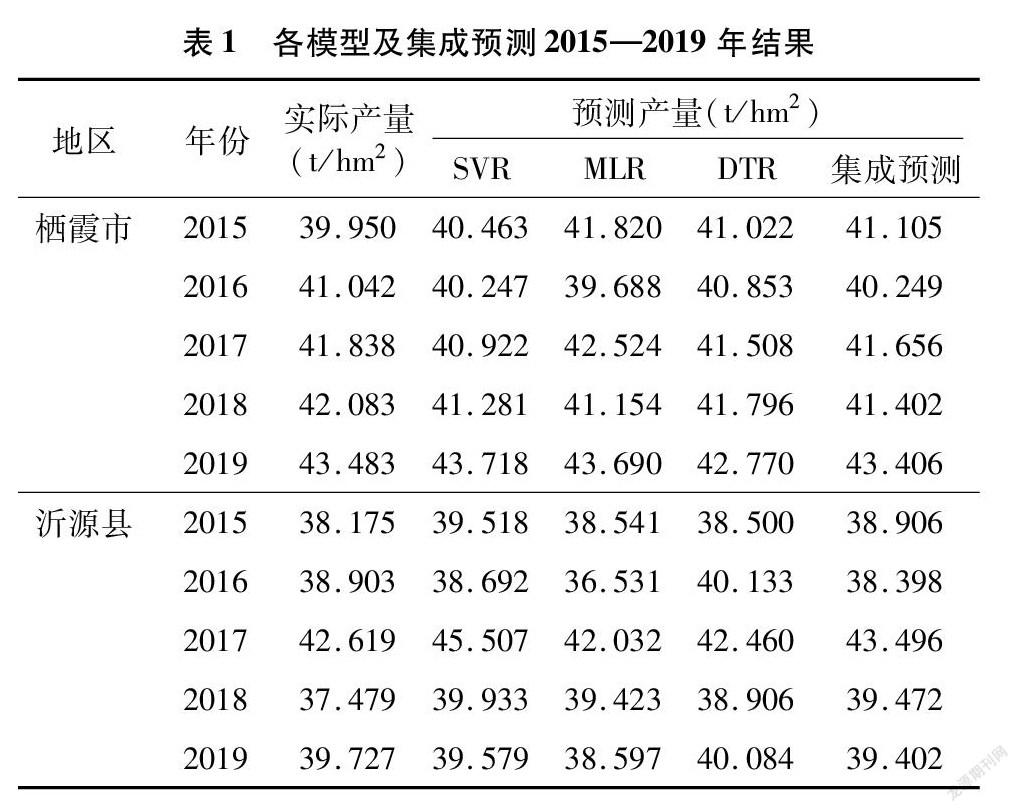
经上述过程筛选出预测变量后，本部分利用SVR、MLR和DTR进行训练并预测，后依据“公式（5）”对3种模型结果进行集成预测。训练时采用循环预测方法，即利用2005—2019年数据时，从2005年开始依次选取1年作为测试集，剩余年份数据作为训练集。此方法相较于1次划分训练集、测试集方法，可提高数据利用效率，更能体现模型预测效果。2个地区3种模型对2015—2019年的预测值见表1，训练集循环预测产量及实际产量趋势见图6。

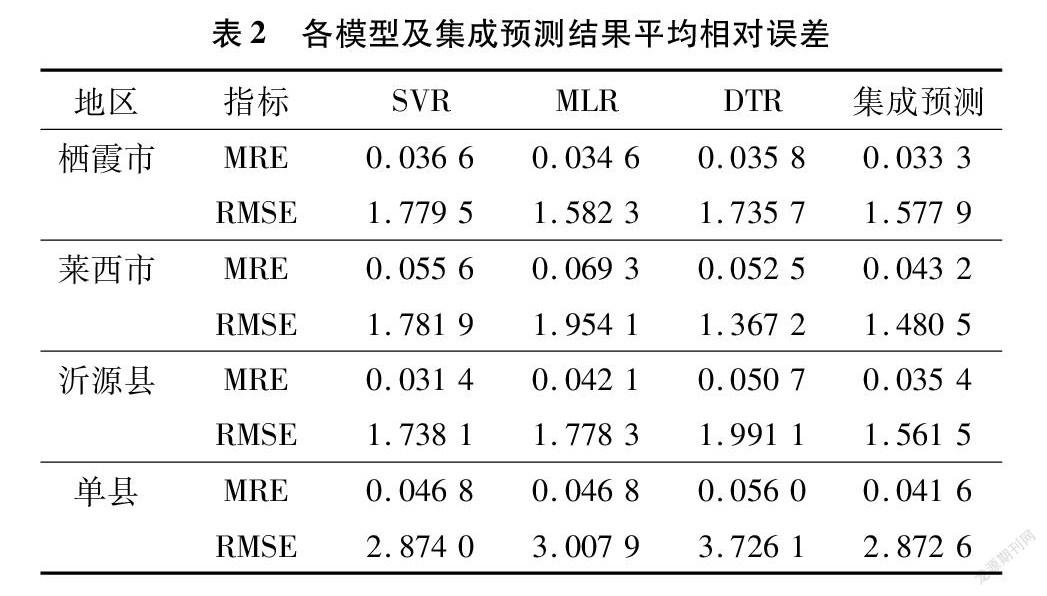
进一步分析栖霞市、莱西市、沂源县、单县4地的循环预测平均相对误差（mean relative error，简称MRE）及均方根误差（root mean square error，简称RMSE），结果见表2。

上述数据中，集成预测值平均相对误差波动范围最小，除沂源县SVR预测值平均相对误差小于集成预测值平均相对误差外，其余单个预测模型预测值平均相对误差均大于集成预测值平均相对误差;

除莱西市DTR预测值均方根误差小于集成预测值均方根误差外，其余单个预测模型预测值均方根误差均大于集成预测值均方根误差。本试验分布于鲁东、鲁中、鲁西，表明集成预测在时间及空间上相较于单一预测模型有更好的预测准确性和稳定性，且集成预测值平均相对误差均小于4.5%，可应用于实际苹果产量预测中。

3 结论

本研究以机器学习理论为基础，建立基于气象数据预测产量的模型方法。通过分离气候产量并与月平均气象数据求解距离相关系数筛选出关键预测因子，建立以支持向量机回归、多元线性回归、决策树回归为基础模型的集成预测模型，对山东省4个主产地2005—2019年数据进行循环预测。预测结果表明，集成预测相较于以上3种单一预测模型表现出更高的预测精度和稳定性，即在4个试验地区中，集成预测相对误差为3.0%～4.5%，均方根误差为1.5～2.6。本研究所用产量预测方法良好，可应用于其他主产县的苹果产量预测中。

参考文献：

[1]束怀瑞，陈修德. 我国果树产业发展的时代任务[J]. 中国果树，2018（2）：1-3.

[2]张 轶，刘布春，杨晓娟，等. 基于农作物灾情的长江中下游地区粮食产量损失评估[J]. 中国农业气象，2018，39（4）：280-291.

[3]房世波. 分离趋势产量和气候产量的方法探讨[J]. 自然灾害学报，2010（6）：13-18.

[4]钱永兰，毛留喜，周广胜. 全球主要粮食作物产量变化及其气象灾害风险评估[J]. 农业工程学报，2016，32（1）：226-235.

[5]白秀广，陈晓楠，郑少锋. 气候变化对苹果主产区单产及单产增长的贡献研究[J]. 中国农业大学学报，2015，20（4）：82-91.

[6]杨小利，江广胜. 陇东黄土高原典型站苹果生长对气候变化的响应[J]. 中国农业气象，2010，31（1）：74-77.

[7]刘 璐，郭 梁，王景红，等. 中国北方苹果主产地苹果物候期对气候变暖的响应[J]. 应用生态学报，2020，31（3）：845-852.

[8]段曉凤，张 磊，金 飞，等. 气象因子对苹果产量、品质的影响研究进展[J]. 中国农学通报，2014，30（7）：33-37.

[9]申顺吏，杨俊梅，巩在武. 基于灰关联的山西苹果产量气候影响因子分析及苹果产量预测[J]. 南方农业学报，2016，47（7）：1146-1154.

[10]杨小兵，杨 峻，杨 晨，等. 安徽省花生产量与气象因素的关联度分析及预测模型研究[J]. 中国农学通报，2020，36（34）：100-103.

[11]易 谆，王晓东，陈 刚，等. 基于灰色预测和线性回归的烟叶产量预测模型[J]. 计算机应用，2013，33（增刊1）：52-54.

[12]史京京，姬铭泽，于立河，等. 运用灰色关联度分析法对黑龙江西部地区引进燕麦品种的综合评价[J]. 江苏农业科学，2020，48（2）：97-103.

[13]王彩峰，史建民. 山东省苹果种植面积的时空演变特征分析[J]. 中国农业资源与区划，2017，38（12）：170-177.

[14]王黎明，吴香华，赵天良，等. 基于距离相关系数和支持向量机回归的PM2.5浓度滚动统计预报方案[J]. 环境科学学报，2017，37（4）：1268-1276.

[15]李鹏飞，王青青，毋建宏，等. 基于BP神经网络、ARIMA和 LS-SVM 模型的集成预测研究：1978—2017年陕西省苹果产量实证[J]. 江苏农业科学，2020，48（4）：294-300.

[16]李 航. 统计学习方法[M]. 北京：清华大学出版社，2012.

[17]王 宁，谢 敏，邓佳梁，等. 基于支持向量机回归组合模型的中长期降温负荷预测[J]. 电力系统保护与控制，2016，44（3）：92-97.

3433501908225