UHPC 力学性能及在桥梁结构中的应用

刘瑜LIU Yu；黄荆HUANG Jing；刘晓贝LIU Xiao-bei

（①北京世纪千府国际工程设计有限公司，北京 100089；②桂林理工大学土木与建筑工程学院，桂林 541004）

0 引言

1944 年，Larrard 和Serran 首次提出了超高性能混凝土UHPC（ultra-high performance concrete）的概念，同年，法国Richard 报道了最具代表性的超高性能混凝土——活性粉末混凝土RPC（Reactive Powder Concrete）[1]。UHPC作为新型材料，具有优异的力学性能，在桥梁、建筑等领域应用广泛。美国、法国等国家近年来颁布了一系列与UHPC 相关的设计施工技术规范，为UHPC 的应用与推广提供了参考依据。本文对UHPC 的基本性能研究成果以及对UHPC 材料在桥梁中的应用做出总结，以期为UHPC 材料与工程实际相结合提供一定的参考。

1 UHPC 的材料性能

与普通混凝土NC（normal concrete）以及高性能混凝土HPC（High Performance concrete）相比，UHPC 材料依据最密实堆积理论设计，有较低的水胶比与内部致密的水泥基石，并且剔除了较大粒径的粗骨料，故其表现出了较强的抗压能力。同时，由于UHPC 材料内部填充了一定数量的钢纤维，使得UHPC 材料在开裂之后，由于钢纤维的存在，使得材料仍具有一定的拉应力，此外，UHPC 的力学性能相比于普通混凝土得到了极大的提高，这决定了UHPC材料在工程中可以广泛的推广及使用以改善传统混凝土结构的不足之处。

1.1 UHPC 的抗压性能

作为混凝土结构的基本力学性能和结构设计的重要参数，抗压强度一直是国内外研究的重点问题。

1.1.1 试件的尺寸效应对抗压性能的影响

作为一种水泥基复合材料，尺寸效应对其抗压强度会产生很大的影响，材料的抗压强度与其尺寸、截面形式等具有一定的相关性。Yuliarti 等[2]研究了立方体和圆柱体两种不同类型、不同钢纤维体积掺量的UHPC 的抗压强度，采用的圆柱体尺寸为100×200mm（直径×高度），立方体试块的边长为100mm。试验结果表明，立方体和圆柱体试样之间不同钢纤维掺量所对应的平均抗压强度转换系数分别为0.89（0%）、0.94（1%）以及0.94（2%），这与之前Leubecher 所提出的转换因子0.96 较为接近。苏捷等[3]设计水胶比分别为0.16、0.18 和0.2 的多个强度等级和纤维掺量的超高性能混凝土立方体试块，由抗压强度试验可知，UHPC 立方体抗压强度与钢纤维的体积掺量以及尺寸效应有关，通过试验得到的各纤维掺量尺寸效应关系提出了UHPC 立方体抗压强度的尺寸效应率。试验结果表明，随着试件尺寸的增大，抗压强度逐渐降低，进一步分析原因发现，试件浇筑成型时，钢纤维的分布会出现“箍筋”一样的边壁效应，且试件的边壁效应与尺寸效应成正相关，即试件尺寸越小，尺寸效应越强。同时，小尺寸试件极易产生钢纤维结团现象，使得尺寸效应加强。Skazlic 等[4]研究了不同尺寸的UHPC 圆柱体试件抗压强度，得到了70×140mm（直径×高度），100×200mm，150×300mm 的试件抗压强度转化系数，其研究分析结果如下：若采用100×200的圆柱体试块作为标准试块，则70×140 以及150×300 的试块抗压强度转化系数分别为1.05～1.15、0.85～0.95。

1.1.2 钢纤维掺量对抗压强度的影响

钢纤维作为UHPC 的重要组成部分，其掺入量对于超高性能混凝土的抗压强度影响显著。沈从春等[5]通过立方体以及轴心抗压强度试验，研究分析了钢纤维掺量分别为0.5%、1%、1.5%、2%以及2.5%时的抗压强度，试验结果显示，在掺量为2.5%时，轴心抗压强度与立方体抗压强度相比于钢纤维掺量为0%的水泥基体分别提高了25.61%以及25.49%，且相同纤维掺量的轴心抗压强度与立方体抗压强度的比值相差较小，其比例系数均稳定在0.86。杨简等[6]分析了对钢纤维掺量以及所掺入的钢纤维长度和直径不同对UHPC 强度的影响，其数据结果如图1 所示。

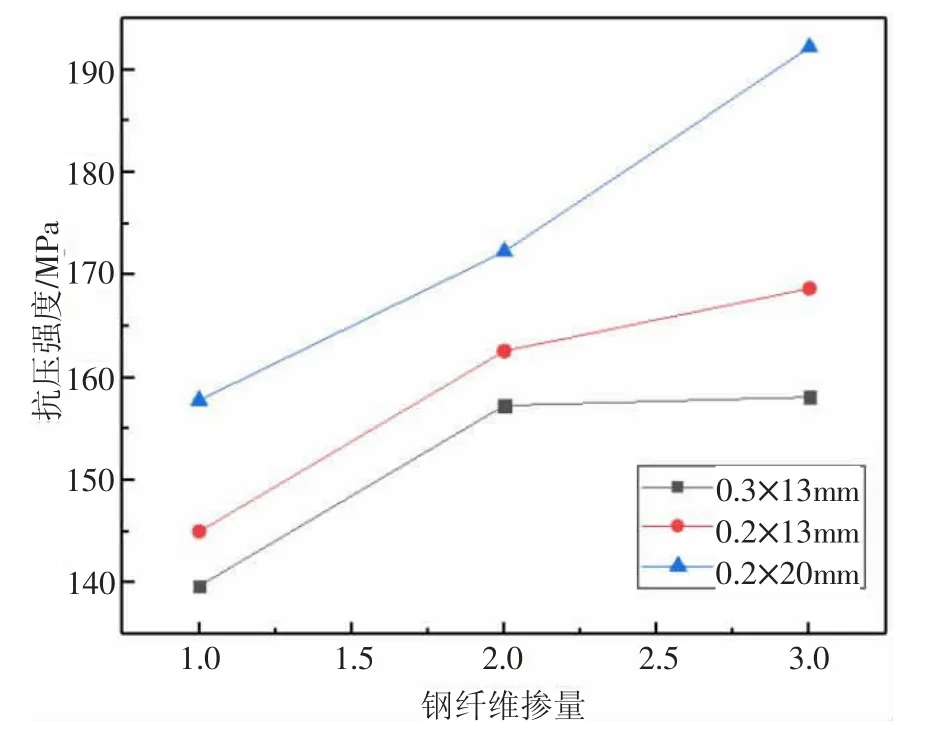
图1 钢纤维掺量对抗压强度影响

经试验结果分析，钢纤维掺量是影响其抗压强度的主要因素，取文献10 中钢纤维掺量为2%的抗压强度数据进行对比分析，抗压强度随长径比的增大而增大。钢纤维掺量越大，其增大的幅度越明显。如图2 所示。

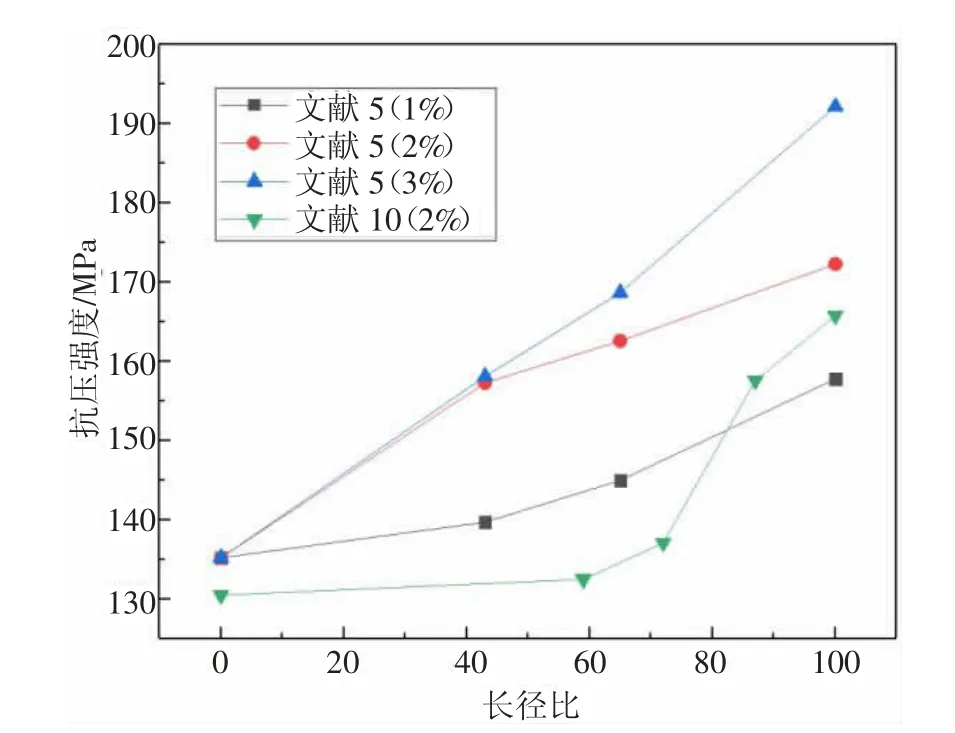
图2 纤维长径比对抗压强度的影响

1.1.3 其他因素对UHPC 抗压强度的影响

除上述影响因素之外，UHPC 材料的抗压强度还受砂的种类、浇筑时间、浇筑温度等多种不同因素的影响。王冠等[7]设计多个对比试验，分析了不同配合比、钢纤维掺量、以及砂的种类对UHPC 材料的影响。试验结果显示，通过提高硅灰的掺量可以提高UHPC 的强度。试验中采用了四种不同砂的类型，分别为海沙、江砂、机制砂以及石英砂，试验结果表明，海砂、河砂中由于存在较多的杂质，且海砂中存在一定的化学反应，会生成一定的渗透性或膨胀性的软物质，在混凝土中形成微小空隙，对抗压产生明显的不利影响，故其强度明显低于石英砂，而机制砂是经过人工破碎而成，表面粗糙且形状不规则，颗粒与颗粒之间的咬合力增强，故其抗压强度最高。Kazemi 等[8]研究发现，浇筑时间对于UHPC 的抗压强度也有一定的影响，并且得到了UHPC 的抗压强度与浇筑时间的关系公式。Craybeal[9]采用相同配比的试件，研究分析了养护温度对UHPC 抗压性能的影响，并通过曲线拟合，得到了养护温度和抗压强度的关系式。

1.2 UHPC 材料的抗拉性能

UHPC 材料由于内部掺加了大量的钢纤维，使得其受拉性能相比于普通混凝土而言得到了很大的提升。以UHPC 板受负弯矩作用为例，当板受到负弯矩作用，上部UHPC 层开裂，水泥基体退出工作，由于钢纤维的桥接作用使其仍具有一定的抗拉强度，故普通混凝土规范中，忽略混凝土的抗拉作用的计算方法并不适用于UHPC 材料，会导致计算过于保守，造成材料浪费。同时，与纤维混凝土相比，UHPC 材料的水泥基体内部致密，因此，UHPC 的水泥基体对于钢纤维的握裹力要远高于普通纤维混凝土。UHPC 材料优良的抗拉性能使得其应用的广度以及应用的范围不断增加，理论体系也日渐趋于完善。

1.2.1 钢纤维对UHPC 材料受拉的影响

沈秀将等[10]对设计的试件进行直接拉伸试验（DTT）、四点弯试验（4PBT）来测试纤维取向分布及UHPC 薄层的抗拉性能，试验结果显示，随着纤维流动距离变化，薄板内的非弹性部分抗拉性能较大，且抗拉强度以及极限应变随纤维流动距离增大而增大。且采用4PBT 试验所得值普遍高于DTT 试验，如图3 所示。

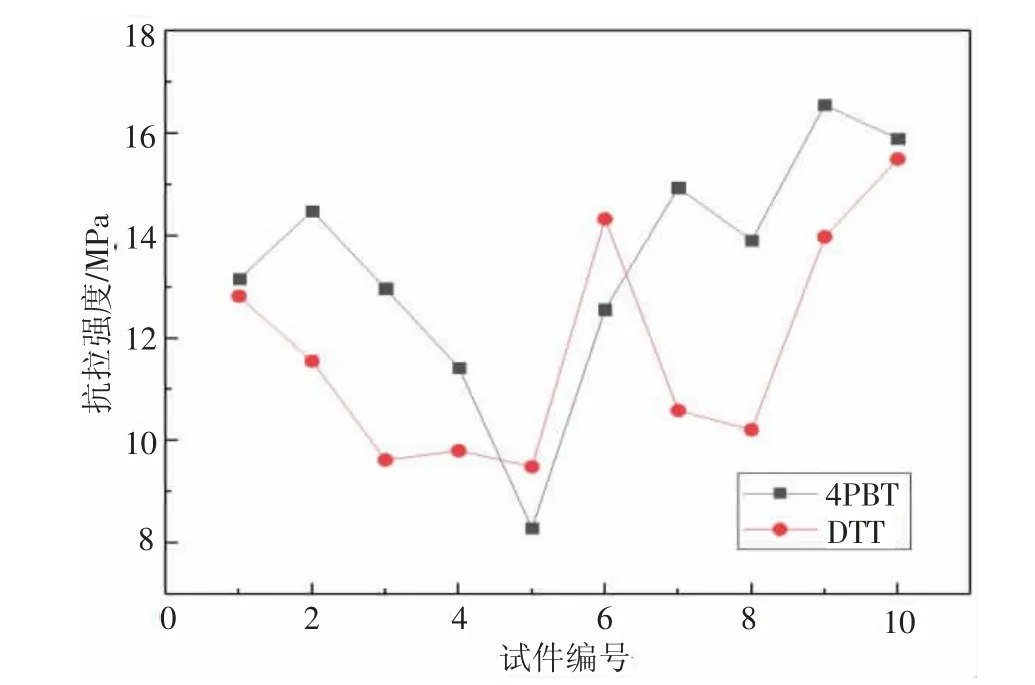
图3 试验类型对抗拉强度的影响

邵旭东等[11]研究了2%钢纤维特性对UHPC 轴拉性能与弯拉性能的影响，设计了500mm×100mm 截面的狗骨头型试件以及100mm×100mm×400mm 的棱柱体试块分别测量试件的轴拉性能以及四点弯拉性能，以瑞士UHPC 指南中所规定的终止条件进行加载，结果显示，混凝土裂缝开裂时只有一条主裂缝，且断裂面呈现弯曲形状，原因在于钢纤维被拔出时为乱象分布。对文献中长径比为59 的端钩型以及平直型试件各应变点绘制应力应变曲线，如图4所示。

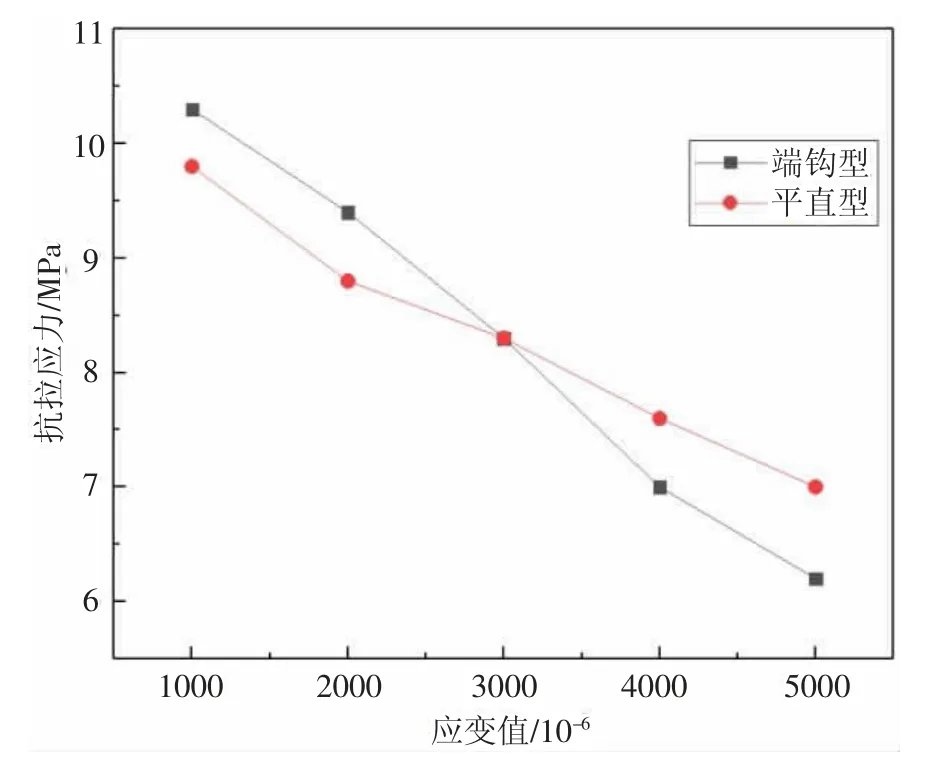
图4 钢纤维类型对拉应力的影响

以轴拉应变为3000×10-6为分界点，在此之前，端钩型试件的轴拉应变大于平直型，当裂缝开展到一定宽度后，由于端钩型试件被拉直的过程中会对水泥基体产生一定的损伤，故平直型试件的轴拉强度反而会强于端钩型试件。

掺入体积为2%的钢纤维，轴拉峰值强度相比于无纤维的强度可以提高约11～12%，弯拉峰值强度可提高0.8～2.0 倍。纤维的长径比对于弯拉的影响比其轴拉更加显著如图1 所示，且其弯拉韧性随着纤维的长径比增加而呈现出了递增的趋势。如图5 所示。

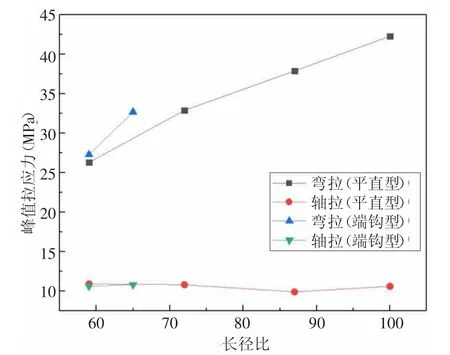
图5 弯拉与轴拉试验

胡翱翔等[12]设计了8 字型试件，通过加大端头两端提拉的方法，研究了钢纤维掺量与抗拉强度的关系，对钢纤维掺量和抗拉强度关系曲线进行曲线拟合后，如图6 所示，得出钢纤维掺量与UHPC 抗拉强度的关系式（1），如下：

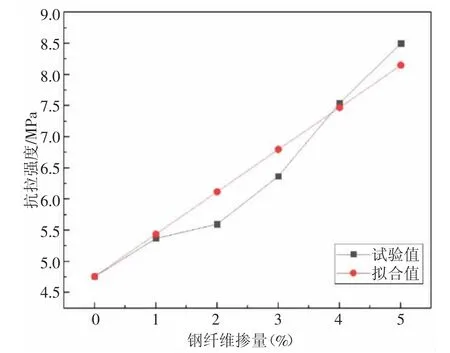
图6 纤维掺量对抗拉强度影响

其中，ft0为不掺加钢纤维时的抗拉强度，Vf为钢纤维的体积掺量，为钢纤维的长径比。

1.2.2 UHPC 的受拉本构关系

张哲等通过设计四种混合钢纤维掺量的棱柱体UHPC 试件，采用直接拉伸的方法，得到不同试件的应力-伸长率曲线以及应力-裂缝宽度曲线，根据试验曲线提出了包含应力-应变关系以及应力-裂缝宽度关系的两阶段本构模型。在UHPC 材料达到极限应变之前采用双线性本构关系[13]。

在应力软化阶段，基于材料的断裂特点，以最小断裂能原理为基础，在Stang 等提出的指数型经验公式的基础上，提出了两种应力-裂缝宽度的关系模型[14]，即指数函数应力-裂缝宽度关系：

双段线性函数应力-裂缝宽度关系[14]，

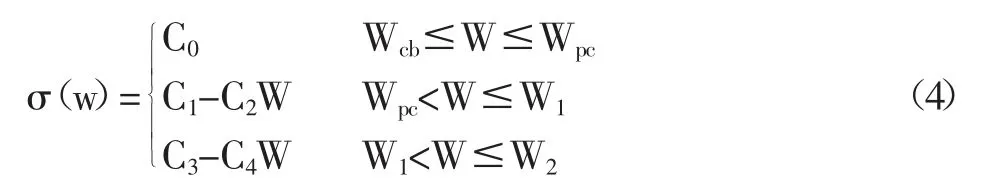
与以往所提出的指数型经验公式模型相比，其优势在于，形式得到了极大的简化，且与试验结果的拟合参数较高，在0.95～1.08 范围内波动。

李立峰等基于双折线本构关系对两阶段拉伸本构模型在应力软化阶段进行了调整，根据法国规范，将应力-裂缝宽度关系转化为应力应变关系后，得到软化阶段的曲线受拉阶段本构关系[15]，即

其中取Wp=1.0mm，p=0.95，εpc=0.002。

胡翱翔等通过以4%的钢纤维轴拉试验得到应力应变关系曲线，根据曲线取其上升段与下降段分别进行分析，分别假设上升段与下降段的方程[12]为：

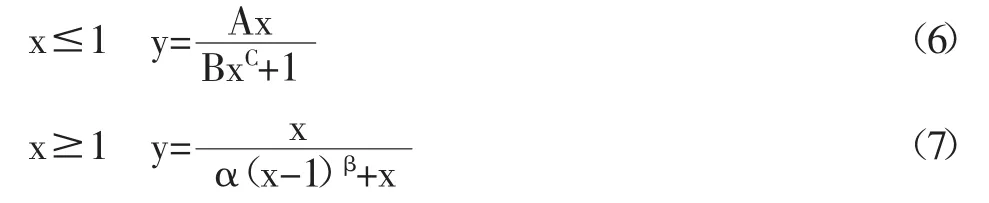
由上升段与下降段的边界条件等，确定方程中各参数值，将各参数带入方程（6）、（7），后通过试验拟合，得到拟合系数为0.025 时效果最佳，故UHPC 的受拉本构[12]为：

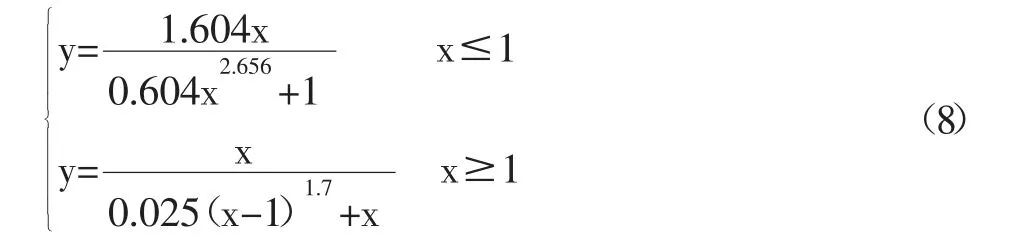
2 UHPC 材料在桥梁工程中的应用

UHPC 材料凭借其优良的力学性能，在桥梁结构中的应用研究日渐增加，由于其具有较好的抗拉强度，故在桥梁工程中，多用于混凝土桥面或钢桥面的桥面板受拉区加固薄层中。

根据UHPC 材料性能方面的优势，针对桥面铺装层易受拉损坏以及疲劳开裂等问题，出现了多种新型桥梁结构形式，邵旭东等[1]提出了三种轻型组合梁的形式，在传统正交异性钢桥面板上铺设UHPC 薄层的轻型组合梁、正交异性钢桥面板UHPC 薄层、钢梁UHPC 薄层，并对这三种新型组合梁的受力机理、静力特性以及疲劳性能进行了分析研究，结果显示，在钢结构的设计范围内，UHPC 层不会开裂，钢-UHPC 组合了的破坏模式是钢结构受压局部失稳，即钢结构先于UHPC 破坏。

为解决钢-混组合梁的负弯矩混凝土板开裂问题，罗兵等[16]提出在组合梁的负弯矩区内采用UHPC 层代替普通混凝土层，通过利用UHPC 材料优良的抗拉性能来减缓负弯矩区裂缝的开展，从而提高组合梁的抗开裂性能。设计三根试验梁进行正位的加载试验，对比分析钢-UHPCNC 组合梁与钢-NC 组合梁受力性能的同时，验证不同配筋率对梁的影响，试验结果表明，UHPC 层裂缝与C50 混凝土层裂缝的分布具有相反的特点，UHPC 层裂缝数量较多，宽度较小，主要集中在跨中区和加载段，当提高UHPC板的配筋率时，较高的配筋率使得结构的应力重分布更加明显，从而使得裂缝的分布相对分散。

而C50 混凝土数量少、宽度大裂缝分布均匀且全截面贯穿。并且，经试验分析发现，通过在梁的负弯矩区加设UHPC 薄层，组合梁在弹性阶段的刚度提升了7～20%，对于其弹塑性和塑形阶段来说，UHPC 层对于刚度的贡献不大，在试验过程中，UHPC 层与NC 层并未发生相对滑移以及粘接破坏，故可证明UHPC 与NC 可以形成较强的组合作用。

类似的刘君平等以某钢-普通混凝土简支组合梁桥为背景，通过设计钢-UHPC 组合梁以及钢-普通混凝土组合梁模型来进行抗弯性能的对比试验，结果表明，两种组合梁的破坏模式，都是钢梁受压屈服后，桥面板的混凝土被压碎，但钢-普通混凝土的破坏形态为加载点处混凝土片状压碎破坏，而钢-UHPC 混凝土的破坏形态则为纯弯段的中部出现范围较小的带状压碎，因此，采用钢-UHPC 组合梁使得破坏时的脆性现象得到了明显的改善，且其剪力滞效应以及钢梁与桥面板间的相对水平滑移均小于钢-普通混凝土组合梁，同时由于UHPC 材料性能远高于普通混凝土材料，故组合梁呈现出“钢梁弱，UHPC 板强”的特点，在设计时，可以考虑降低UHPC 板的厚度，相同的抗弯极限承载力的条件下，UHPC 板相比于普通混凝土板可以减薄28%。

朱劲松等[17]通过设计4 根钢-UHPC 华夫组合梁开展了负弯矩抗弯性能的试验研究，对比分析了板肋高度比，配筋率等因素对钢-UHPC 华夫组合梁承载力的影响。

3 结束语

综上，UHPC 力学性能优异，使得国内外对于该种材料的研究形成了初步的理论体系，但仍然存在许多不足之处。

对于钢纤维的掺量、类型等对UHPC 强度影响的研究已经十分充分，但对于UHPC 制备工艺的研究还需进一步完善。

且对于钢纤维的研究性能较为分散，均只是针对某一点的性能进行研究，如何得到包含经济性在内的综合性能最优配比，成为目前面临的一个重要的问题。

混杂钢纤维可以提高UHPC 的抗拉强度、极限应变等，但对于混杂型纤维的掺加比例，以及其对UHPC 的影响系数等还需进行进一步做定量研究。

UHPC 薄层现多应用于桥面板结构中，由于UHPC 桥面板的优异力学性能，使得UHPC 层可以很薄，钢板与UHPC 采用栓钉连接，当UHPC 层很薄时，需进行栓钉形式上的创新，如何创新栓钉的结构形式是进一步发展UHPC 组合梁的关键。