双鱼石超深高温高压气藏偏差因子计算方法及早期储量预测
邓 波,陆正元,刘奇林,罗 静,刘斯琪,彭 杨,熊 钰
(1.成都理工大学,四川 成都 610059;2.中国石油西南油气田分公司,四川 绵阳 621700;3.中国石油西南油气田分公司,四川 成都 610213;4.西南石油大学,四川 成都 610500)
0 引 言
动态储量计算方法主要包括压降法、弹性二相法等动态分析方法,计算中主要涉及偏差因子、综合压缩系数2个关键参数。目前天然气偏差因子预测常用方法为DPR、HY和DAK方法[1],均可为常压气藏提供较准确的计算结果[2],预测相对误差为1.0%左右,而计算超深高温高压气藏的动态储量对偏差因子预测误差要求更小。针对超深高温高压气藏的动态储量计算,中国学者开展了大量研究。李大昌等[3]、张迎春等[4]揭示异常高压气藏压力下降曲线呈抛物线趋势;杨露等[5]综合分析了异常高压气藏动态储量计算的6种动态分析方法,给出了不同方法的适应条件和范围;赵健等[6]将碳酸盐岩缝洞型油藏储层储集结构分为溶洞型、孔洞型和裂缝型,研究了3种储集类型综合作用对气藏动态储量计算参数的影响;成友友等[7]研究压缩系数对动态储量计算的影响时,修正了常规气藏储量计算方法中的压力参数,进而利用压降曲线的拐点位置建立了新的虚拟储量校正方程。在超深气藏动态储量计算研究中,大多考虑如何修正储量计算方法,而对如何获取准确的计算参数关注度不够。因此,该文基于PVT实测偏差因子数据,建立了气藏偏差因子数学计算模型,讨论了超深层碳酸盐岩储层压缩系数的基本特征及对动储量计算的影响,为准确计算早期动态储量提供参考借鉴。
1 超深层高温高压气藏偏差因子计算新方法
双鱼石区块位于四川盆地西北部,该区块栖霞组气藏压力为95~98 MPa,地层温度为154.25~169.64 ℃,H2S含量为0.34%~0.41%,CO2含量为1.40%~2.00%,气藏埋深大于7 000 m,属于超深层高温高压气藏。计算超深层高温高压气藏动态储量时,由于其地层压力接近100 MPa,偏差因子误差达到1.00%时,井底流压误差接近1 MPa,如果偏差因子误差能够低于0.50%,将使动态储量计算结果得到较大提高。因此,有学者认为在超高压阶段,偏差因子与压力呈线性关系,可采用对不同温度下的高压阶段数据线性外推求取偏差因子[8-11],但该方法运用到四川盆地西北部栖霞组超深层气藏时发现,由于早期压降测试数据点在2个实测偏差因子压力点之间,采用线性内插计算气藏单井早期动态储量明显过大。要建立针对任何高温高压气藏都适用的高精度方法,需要多元回归与检验,或者基于维利状态方程的拟合,在截断误差分析基础上,求取回归方程。因此,采用Mahmoud[12]提出的DAR方法,公式如下:

(1)
式(1)可简化为关于ppr的二次方程式,其中,系数a、b、c只与温度有关:
(2)
式中:Z为无因次偏差因子;Tpr为无因次拟对比温度;ppr为无因次拟对比压力。
利用式(1)计算双鱼石区块栖霞组气藏偏差因子曲线,并与实验数据进行对比(图1)。研究中首先考虑压力对预测结果的影响,在多组数据误差分析基础上发现式(2)中的系数a影响较小,预测偏差主要源于系数b、c。因此,首先改进方程系数b,获得了一定温度下的高精度预测结果,如图2所示,实验数据与改进系数b后DAR方程预测结果接近。
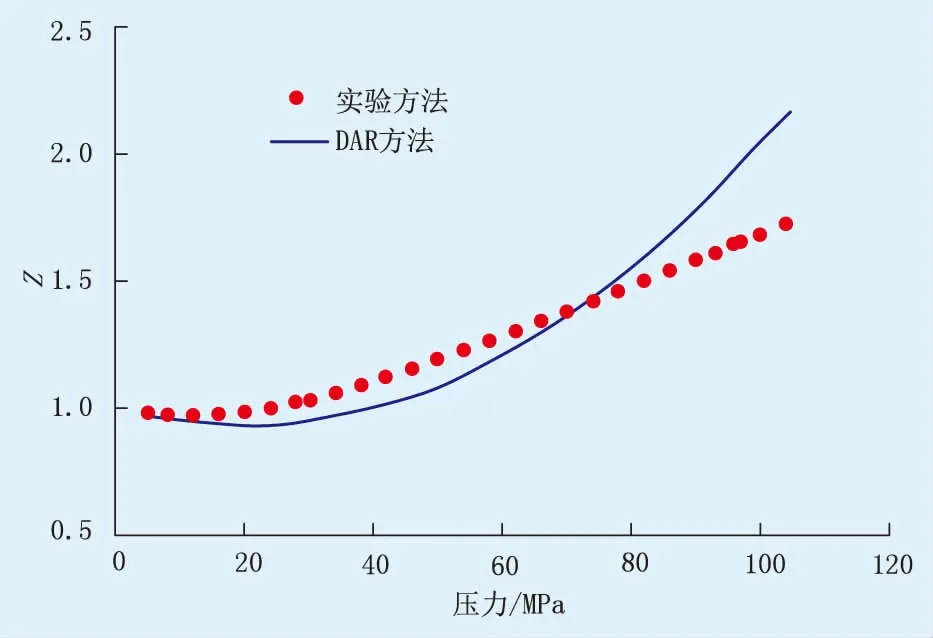
图1 DAR方程计算和实验测得偏差因子对比(134.5 ℃)
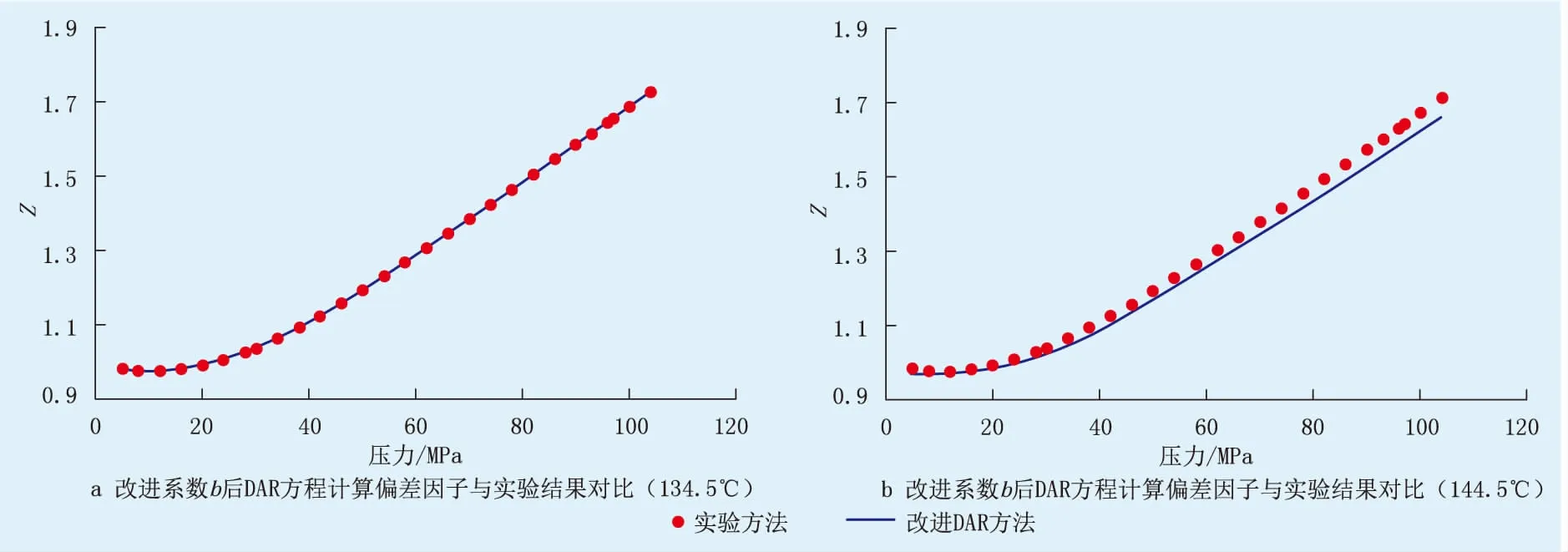
图2 改进系数b后DAR方程计算偏差因子与实验结果对比
相同压力下,计算134.5、144.5、155.5、165.5、174.5 ℃时改进系数b后的偏差因子并与实验结果进行对比,发现在高温下误差增大,推测是式(2)中系数c的影响造成。将同一压力下的5个不同温度的误差值对应排列起来,得到关于Tpr、ppr2个自变量的误差(图3)。对图3所示的误差进行多元函数拟合,得到改进后的系数c。
在获得系数c的表达式后,将系数a、b、c代入式(2),获得误差函数分析和多元参数拟合的偏差因子预测方程,建立了新的偏差因子计算模型。

(3)

图3 温度、压力与偏差系数误差曲线
根据双鱼石区块栖霞组气藏流体组分数据(表1),计算天然气临界压力、临界温度及不同温度、压力下的拟临界温度、拟临界压力,再用式(3)计算的偏差因子与气藏各温度下实测的偏差因子对比,结果如图4所示。可见改进的DAR方法计算的天然气偏差因子值与实验数据值几乎完全一致,与其他偏差因子预测方法相比(表2),误差更小,说明改进的DAR方法可以获得非常准确的偏差因子,因此,改进的DAR方法是双鱼石区块栖霞组气藏开发早期动态储量准确计算的重要技术之一[13]。

表1 双鱼石区块栖霞组气藏天然气组分构造

表2 不同Z因子预测方法计算结果对比表

图4 不同温度下的DAR方法计算结果与实测数据对比
2 超深层高温高压气藏的压缩系数
超深气井是指深度为6 000~9 000 m的气藏井[14]。超深气藏温度和压力较高,按压力、温度等级衡量属于高温高压气藏。目前对超深层高温高压气藏渗透率、应力变化等实验测试分析较为常见[15-17],对压缩系数的研究相对较少,主要是因为岩石的压缩系数可以通过孔隙度应力敏感实验求取,但因为这种方法使用标准柱塞岩样,对于缝洞和孔洞型碳酸盐岩,小柱塞岩样会导致结果出现较大偏差。
在弹性二相法储量计算中气藏压缩系数的定义为:
Ct=CgSgi+CwSwi+Cf
(4)
考虑应力作用下的物质平衡方程中,气藏的压缩系数定义为:
(5)
式中:Ce为原生水和岩石的综合弹性系数,MPa-1;Sgi为初始条件下的含气饱和度,%;Swi为初始条件下的含水饱和度,%;Ct为综合压缩系数,MPa-1;Cg、Cw、Cf分别为天然气、地层水和岩石的压缩系数,MPa-1。
由式(4)、(5)可知,气藏的压缩系数与地层水压缩系数、岩石压缩系数有关,在储量计算时如果仅考虑天然气的压缩性,将产生较大的误差。
2.1 地层水压缩系数
通常认为地层水的压缩系数为3.7×10-4~5.0×10-4MPa-1。高温高压气藏中地层水压缩系数的实验数据较少,通过多种经验方法试算得到的地层水压缩系数均不在合理范围内。实际上,地层水的压缩系数需要考虑高温高压下天然气溶解系数[18],据文献调研结果,气体实测平均溶解系数取值为0.105 159[19],通过式(6)求解天然气溶解度,并根据式(7)计算地层水压缩系数[18]。如根据双鱼石区块栖霞组的温度、压力及矿化度等数据,求得Cw为0.000 759 5 MPa-1,显然其值明显高于通常认为的数据范围。
Rsw=αwp
(6)
Cw=1.4504×10-4[A+B(1.8T+32)+C(1.8T+32)2]×(1.0+0.049974Rsw)
(7)
A=3.8546-1.9435×10-2p
(8)
B=-1.052×10-2+6.9183×10-5p
(9)
C=3.9267×10-5-1.2763×10-7p
(10)
式中:Rsw为天然气在水中的溶解度,m3/m3;αw为天然气溶解系数,m3/m3;p为地层压力,MPa;T为地层温度,℃。
2.2 岩石压缩系数
常规砂岩油气藏岩石压缩系数一般为1×10-5~2×10-5MPa-1[20],而地层水的压缩系数高于岩石压缩系数1个数量级,故通常认为岩石不可压缩、地层水微可压缩。对于超深层高温高压气藏,该常规认识并不完全适用,这也是试采早期双鱼石栖霞组碳酸盐岩气藏动态储量计算误差较大的原因之一。主要是由于碳酸盐岩中发育裂缝和溶洞增加了其岩石应力敏感性,从而增大了岩石的压缩系数[21-22]。双鱼石碳酸盐岩岩心应力敏感实验结果也反应了这种规律性,如图5所示,即碳酸盐岩气藏从孔隙型储层到裂缝孔洞型储层,所测试的岩石压缩系数是增大的,裂缝和溶蚀洞的增加会导致岩石压缩系数增加。

图5 孔隙度应力敏感曲线
刘传喜等[23]对迪那砂岩气藏和川东北河坝区块的碳酸盐岩岩石压缩系数进行了研究,认为随着地层有效应力增加,岩石压缩系数大幅下降,因此,认为气藏早期压缩系数相对较大。GUEHRIA[24]通过多项式回归建立河坝区块碳酸盐岩气藏的岩石压缩系数计算方法,该方法计算双鱼石栖霞组气藏岩石压缩系数Cf为0.002 288 MPa-1,与疏松砂岩的压缩系大致相当[25],认为计算结果偏大。
为了较为准确地计算双鱼石栖霞组气藏早期动储量,采用全直径样品进行压缩系数实测数据,以减小标准柱塞样品中可能因溶蚀孔洞不发育带来的影响,实测结果Cf为0.000 649 7 MPa-1,说明超深层高温高压气藏的岩石压缩系数和地层水压缩系数相近,表现为微可压缩特征。因此,在超深层高温高压气藏动态储量计算时,不能按常规油气藏考虑,其岩石压缩特性不可忽略。
3 对比分析与评价
以双鱼石栖霞组气藏双鱼001-1井为例,其所在构造圈闭面积为31.61 km2,采用容积法计算区块探明储量丰度为2.48×108m3/km2,探明地质储量为78.39×108m3。计算双鱼001-1井早期动态储量,首先忽略岩石和束缚水的弹性膨胀,分别采用改进DAR方法和线性内插方法[11],压降算法公式如下:
p/Z=pi/Zi(1-Gp/G)
(11)
式中:pi为原始地层压力,MPa;Zi为原始地层压力下的偏差因子;Gp为累计产气量,108m3;G为动态储量,108m3。
采用改进DAR方法和线性内插方法分别计算双鱼001-1井早期动态储量,发现2种方法计算的压降曲线相差较大,其原因主要是实验时一般按3 MPa逐级降压测偏差因子,压降区间较大导致高压阶段偏差因子看似线性变化,而实际上高温高压气藏的偏差因子在高压阶段并不是线性变化。由图6可知:不同方法求得的动态储量相差较大,利用改进DAR方法计算的偏差因子得到的动态储量为98.75×108m3,利用线性内插法得到的偏差因子计算动态储量为113.01×108m3,二者储量相差14.26×108m3。而采用DPR、DAK和HY方法计算偏差因子,得到的动态储量分别为97.87×108、103.29×108和99.83×108m3。在忽略岩石和束缚水的弹性膨胀的情况下,采用以上5种方法计算得到的动态储量均明显高于探明地质储量,与开发常识相悖,表明高温高压气藏计算动态储量时不应忽略岩石和束缚水的弹性膨胀影响。

图6 双鱼001-1井动态储量计算结果
超深高温高压气藏岩石的压缩特性已达到微可压实阶段,因此,开采初期不考虑气藏水侵时,动态储量的计算应考虑弹性能量的影响,即使用物质平衡通用表达式:
p/Z(1-CtΔp)=pi/Zi(1-Gp/G)
(12)
式中:Δp为原始地层压力与当前地层压力的差值,MPa。
利用双鱼石栖霞组全直径岩心实测压缩系数和地层水压缩系数,通过式(12)计算双鱼001-1井动态储量为76.25×108m3,而文献[23]计算的动态储量为54.86×108m3,因为岩石综合压缩系数取值不同,二者动态储量计算结果相差19.39×108m3。由于区块处于开发早期,累计产气量为5.07×108m3,探明地质储量为78.39×108m3,早期动态储量为76.25×108m3较为可靠,误差为3.8%,认为偏差因子和综合弹性系数均为合理的实验结果。采用DPR、DAK和HY方法计算偏差因子及实验获得的综合压缩系数计算的动态储量分别为80.96×108、80.24×108、78.14×108m3,计算结果偏高,与改进DAR方法计算的早期动态储量对比,误差分别为10.4%、9.4%和6.6%,预测新方法较以往常规方法,早期动态储量预测准确度可提高3.0个百分点以上。
4 结 论
(1) 基于新型DAR方法,采用多元回归建立无因次拟对比温度、压力的自变量函数,通过与实验数据对比分析不断修正方程,提出新型超深层高温高压气藏偏差因子计算方程。
(2) 偏差因子和综合压缩系数是早期动态储量计算的2个关键参数;高压阶段,超深高温高压气藏的偏差因子与压力不为线性关系,而实验测试数据之所以显示其具有较好线性关系的特征,是由于实验测试压力间隔较大造成的,因此,计算超深高温高压气藏早期动态储量,采用线性内插和线性外推方法将产生一定误差,文中建立的偏差因子预测新方法较以往常规方法,早期动态储量预测准确度提高3.0个百分点以上。
(3) 超深高温高压气藏储层在高压阶段具有微可压缩特征,其压缩系数的数量级与地层水相当,地层弹性能量较大;早期动态储量计算时,不能忽略岩石的微可压缩特征,取准岩石压缩系数是超深高温高压气藏准确计算早期动态储量的关键参数之一。

