降雨及库水位影响下麻地湾滑坡地下水响应特征分析
檀梦皎,殷坤龙,付智勇,朱春芳,陶小虎,朱延辉
(1. 中国地质调查局南京地质调查中心,江苏 南京 210016;2. 自然资源部流域生态地质过程重点实验室,江苏 南京 210016;3. 中国地质大学(武汉)工程学院,湖北 武汉 430074;4. 武汉大学水利水电学院,湖北 武汉 430072)
0 引言
国内外学者对库岸滑坡变形特征及诱因进行系统分析后普遍认为库水位变动及持续降雨对库岸滑坡发育与变形的影响显著[1−5]。许多学者通过对滑坡专业监测数据的解析,分析了库水位变化和降雨对地下水位变动和滑坡变形的影响。目前研究滑坡地下水响应规律的方法主要有:建立实时监测系统[6]、统计学模型[7]、数值模拟[8−10]以及建立水文模型[11]。这些方法各有优缺点:长时间序列实时监测系统所得到的数据最符合实际,但会耗费巨大的人力物力;统计学模型可以很好地统筹历史数据,寻找数据规律,但是对未来的多变情况包容性不强;数值模拟能尽量模拟真实状态,但是在考虑降雨入渗滞后性以及复杂工况条件下的计算略显不足。现有的解析及数值方法计算的结果和实际情况仍有一定的差距。因此,需要借助地下水专业监测结果对参数进行反演,从而对模型进行修正。
自2003年三峡水库开始周期性蓄水后,库区的地质环境条件被极大地改变。周期性的水位波动以及巨大的水位差(约30 m)对库区内库岸边坡的稳定性产生了较大的影响[12−13]。据不完全统计,库区内有崩塌滑坡堆积体4 000多处,近六成为涉水滑坡[14]。这些滑坡一旦发生大规模坡体失稳,将对人民生命及财产安全造成巨大威胁[15−18]。文中研究区位于重庆市万州区,地处三峡库区腹心。地层多为侏罗系易滑地层,威胁着滑坡附近居民的生命财产和长江航道的安全。三峡库区内库岸堆积层滑坡稳定性受滑坡体内的地下水水位影响,而滑坡体内的地下水水位又与降雨和库水水位联系密切。因此,应用合理的方法揭示滑坡体内地下水对降雨、库水位等外界因素的响应规律对于判断坡体成灾机理和预测坡体稳定性状态至关重要。
依据实际工况条件,文章以三峡库区麻地湾滑坡STK1、STK2、STK3三个水文孔的长序列观测数据为主要研究对象,基于因果检验和数据分析揭示麻地湾滑坡地下水对库水位和降雨响应的滞后性与两种因素共同作用下的响应幅度规律[19−20]。
1 理论方法
1.1 Granger因果检验
Granger因果检验(Granger causality)是由Clive W.J. Granger等于2003年提出的可以判别两个时间序列之间有无因果关系的统计学方法[21]。如果在知道变量X的过去信息和变量Y的过去信息的前提条件下预测Y的效果比仅靠Y的过去信息预测Y有提升效果,则认为X是Y的Granger原因。另外,变量滞后期的不同会对Granger因果检验的结果有很大影响,利用这一特点,可以通过Granger检验从统计学角度验证滑坡地下水的影响因素,并确定地下水响应的最佳滞后期。
对时间序列X、Y进行Granger检验前需要验证其平稳性,常用的统计学方法是ADF检验(Augmented Dickey-Fuller test)[22]。ADF原假设为:序列存在单位根(也就是非平稳),如果在给定的置信水平上显著拒绝原假设,则能证明一个时序数据平稳。若得到的T统计量显著小于3个置信水平(1%、5%、10%)的临界统计值,同时T统计量对应的概率值P值接近0(一般认为小于0.05),则拒绝原假设,即序列平稳。通过平稳性检验的各时间序列可以进行Granger因果检验。Granger检验的思路是首先提出原假设H0:时间序列X不是造成时间序列Y产生变化的原因。
然后利用公式(1)对数据进行预处理:

式中:UR——代表有约束回归模型;
φ1——常数项;
p、q——时间序列Y和X的最大滞后期数;
αi、βi——系数;
Xt−i、Yt−i——t-i时刻的观测值;
µ1t——白噪声;
R——代表无约束回归模型。
针对式(1)构建F统计量进行F检验:
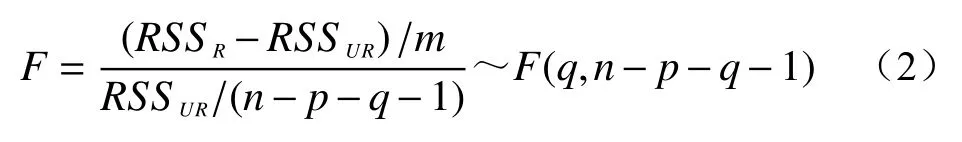
式中:RSSUR——包含X滞后项回归的残差平方和;
RSSR——不包含X滞后项回归的残差平方和,n为样本容量。
检验原假设H0就变成了检验H0=α1=α2=αk=0是否成立。如果F>Fα(q,n−p−q−1) ,则说明β1、β2、···、βk显著不为0,即拒绝原假设,证明了X能够引起Y的变化。
1.2 Apriori算法
关联规则挖掘被广泛应用于基因生物学、网络监测等领域(Association rule mining),该方法可以从大量数据中挖掘数据集间的关联关系[23−24]。
关联规则挖掘算法分为机器学习和非机器学习算法,机器学习算法通过构建和训练模型进而实现数据分析,而非机器学习算法则是直接分析原始数据,不断挖掘数据背后的信息。文中采用的是由AGRAWAL等[25]于1994年提出的代表性非机器学习Apriori算法。
数据集中不可分割的最小单位信息称为项,用符号i表示,I={i1,i2,···,id} 则为所有项的集合,事务T={t1,t2,···,tN}是 项的集合(T⊆I)。设X和Y是项目I的真子集(满足X⊆T,X∩Y=∅,X∩Y⊆T),X为规则的前项,Y为规则的后项,关联规则是形如X→Y的表达式,表示前项的出现对于后项出现的影响。通过关联规则挖掘,可以发现大量样本数据的内在关联信息。然而不是所有关联规则都有意义,需要根据人为设定的最小支持度和最小置信度以及提升度筛选出有实际意义和作用的规则。
支持度(S)是衡量关联规则出现普遍性的指标,即数据集中包含X∪Y的概率百分比,支持度的定义为:
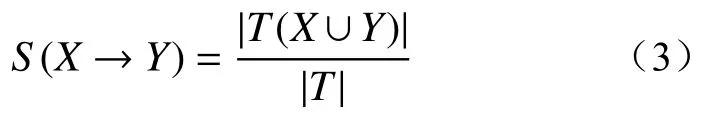
置信度(C)表示X出现条件下Y出现条件的概率,表征关联规则准确度的指标,置信度的定义为:
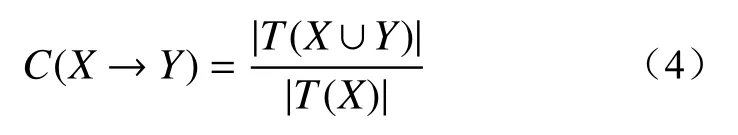
提升度(L)用于衡量关联规则的有效性,小于1时,L意义较弱,而当提升度大于1时表明X的出现对Y的出现具有促进作用,提升度的定义为:
关联规则挖掘简单来说分为两步:①产生频繁项集:即发掘满足最小支持度阈值的所有项集;②产生规则:从上一步发现的频繁项集中提取拥有高置信度的规则。
对每个频繁项集L及其非空子集L′计算置信度,如果置信度大于设定的最小置信度C(L→L−L′)=m in_confidence,即可产生关联规则L→L−L′。
1.3 论文框架
文中结合麻地湾滑坡长时间序列地表位移监测数据确定滑坡外在影响因素,并探究滑坡地下水位在单一要素影响下的变动规律。首先利用Granger因果检验确定地下水响应滞后期,然后基于地下水响应滞后期,确定影响麻地湾滑坡地下水位的影响因素并对其进行定量化,最后通过Apriori数据挖掘算法揭示地下水在不同降雨条件和不同的库水位变动状态下的变化规律。论文思路框架如图1所示。

图1 地下水响应特征研究流程图Fig.1 Research flow chart of groundwater response characteristics
2 工程应用
2.1 滑坡工程地质概况
麻地湾滑坡位于重庆市万州区溪口乡其林村2组,三峡库区万州段南岸。该区域多年平均降雨量达到1 191 mm,4−10月降水量占全年的80%以上。该滑坡处于三峡水库周期性升降变动带范围内,滑坡的形成与发展受水库水位变化影响。2009年8月起,三峡水库开始了每年从175 m下降至145 m再上升至175 m的库水位变动过程。根据具体调度,可以将库水位一年的变动状态分成五个阶段[26]:缓慢下降期(Ⅰ)、快速下降期(Ⅱ)、低水位波动期(Ⅲ)、蓄水期(Ⅳ)和高水位期(Ⅴ)(图2)。

图2 三峡库区库水位变化图Fig.2 Water level fluctuation chart of the Three Gorges Reservoir
麻地湾滑坡平面形态呈箕形,剖面形态呈线形,前缘略微凸起,平均厚度20 m,平均坡度15°,主滑方向为305°,滑坡长570 m,宽330 m,面积18.8×104m2,体积3.76×106m3,为土质滑坡。
据现场调查,滑坡表层主要为第四系崩坡积含碎块石的可塑-硬塑状态粉质黏土,滑带位于第四系滑坡松散堆积层与基岩接触面,呈折线形,物质成份主要为粉质黏土夹碎石、角砾组成。下伏基岩为侏罗系中统新田沟组(J2x)灰色砂岩、紫红色泥岩互层,层厚约10 m,岩层产状334°∠15°(图3)。
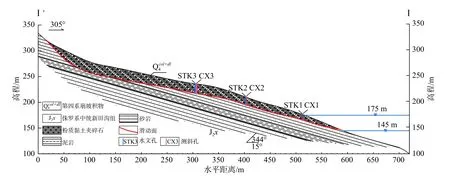
图3 麻地湾滑坡Ⅰ-Ⅰ′剖面示意图Fig.3 Ⅰ-Ⅰ′ Cross-section of Madiwan landslide
2.2 滑坡变形监测
麻地湾滑坡为复活型老滑坡,2003年三峡水库蓄水之前几乎无变形痕迹,2004年后重新开始活动,2011年6月前后,滑坡又发生局部变形,滑坡前缘多处民房水泥地面出现拉裂缝,滑坡中后部滑坡变形不明显。为掌握滑坡变形发展动态,探究其影响因素,在坡体上按照三条纵向剖面线布设9个GPS监测桩(仪器采用亿拓公司YC0600系列地表位移监测仪器,水平精度3 mm±0.1 ppm RMS),监测滑坡的地表位移情况。另外,沿着主剖面布设三套深部位移监测系统和半自动地下水水位监测系统(MicroDiver半自动地下水位计,精度为全量程的0.05%,埋设深度为该点最低平均水位面以下5 m)(图4)。
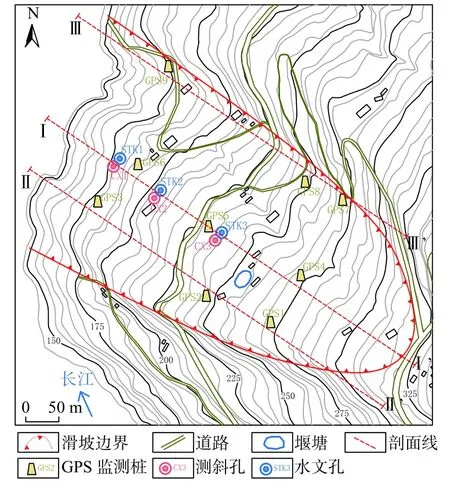
图4 麻地湾滑坡监测仪器布置图Fig.4 Layout map of monitoring equipment on the Madiwan landslide
2.3 滑坡变形影响因素分析
(1)降雨
降雨对于滑坡稳定性的影响可以用位移来展现(降雨数据来源于溪口乡的翻斗式自动雨量计,数据采集间隔为1 h)。图5为降雨量与月位移变化量关系图,标黄部分说明GPS波动较大。从图5中可以看出,滑坡月位移变化量高值区间与高降雨量区间重合度较高(尤其是位于滑坡中后部的GPS1、2、4、5、7、8),说明降雨对于麻地湾滑坡发生地表变形尤其是中后部位的变形有一定影响。
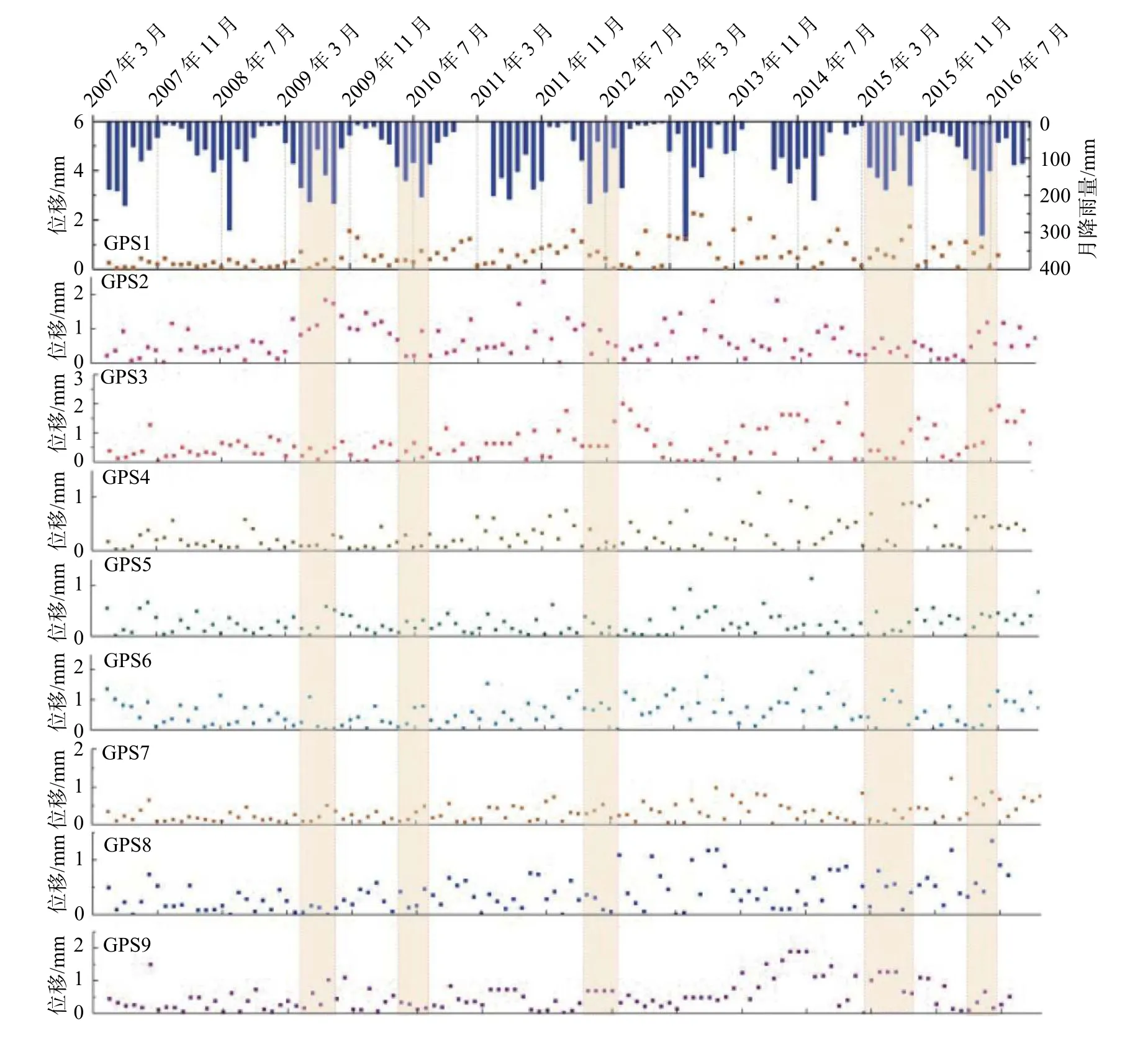
图5 地表位移变化速率与降雨时间序列图Fig.5 Time series of the monthly surface displacement velocity and monthly rainfall
(2)库水位
2009年8月,三峡水库开始175~145 m周期性的蓄降水过程(水位信息来源于长江航道局官方网站)。图6为库水位与月位移变化量关系图,标黄部分说明GPS波动较大。从图6可以看出,在2009年之前,水库最高水位仅在145 m左右(2008年实验性蓄水位达到175 m除外),滑坡月位移变化量最大值在1 mm以内,而2009年后各监测点的月位移变化量最大值提升约50%,这点在位于滑坡最前缘的GPS1上体现得尤其明显。另外,当库水位保持在高水位或者低水位时期时,滑坡月位移变化量较小,而当库水位快速上升或下降时,滑坡月位移变化量呈增加趋势,各GPS点所反映的滑坡月位移变化量高值区与库水位快速升降期同样有较高重合度,说明库水位变动同样可能促使滑坡发生变形[26]。

图6 地表位移变化速率与库水位变化时间序列图Fig.6 Time series of the monthly surface displacement velocity and reservoir water level
3 滑坡地下水响应特征
3.1 麻地湾滑坡地下水整体变动规律
通过在滑坡体上布设的半自动地下水水位监测系统测量得到的多年地下水水位变动数据。如图7所示,麻地湾滑坡地下水变动幅度随着与库水位水平距离的增加而减少。位于滑坡最前缘的STK1处地下水最大变幅可以达到10 m;滑坡中部地下水位受库水位波动影响稍小,最大水位高程差达6 m,且地下水变动有突升突降的特点(STK2);滑坡中后缘处离库水最远,整体水位波动最小,最大水位变动约4 m(STK3)。
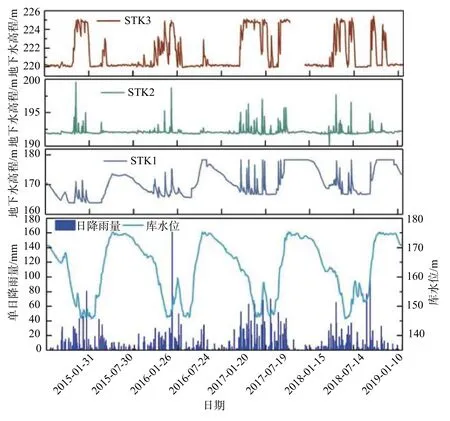
图7 麻地湾滑坡地下水位监测曲线Fig.7 Monitoring curve of Madiwan landslide groundwater
3.2 库水位和降雨对地下水水位影响
(1)降雨
为减少库水位变动因素干扰的影响,选取库水位稳定时期分析此时段内不同水文孔的地下水位对于降雨的响应情况(图8)。
图8涵盖了两种常见降雨类型:多日分散降雨(图8(a)、(b))和单日集中降雨(图8(c)、(d)),(a)的多日降雨总量高于(b),(c)的单日降雨量高于(d)。从降雨总量这一数量关系考虑,当降雨量增加,不同位置处的地下水位上升幅度都将增加,当多日降雨量或单日降雨量较高时,会引起坡面径流量增加,大量水流汇入坡脚,引起位于坡脚的STK1水位抬升远超STK2和STK3的地下水位抬升(图8(a)、(c));当多日或单日降雨量稍小时,降雨有充分的时间入渗土体,位于滑坡中后缘的STK3地下水位升高明显,升高趋势与STK1相当甚至超过STK1(图8(b)、(d)),在三个水文观测孔中,STK2的变化幅度始终都是最小的。当降雨为单日集中降雨雨型时可以从图中看出明显的响应滞后(图8(c)、(d)中的Lag)。
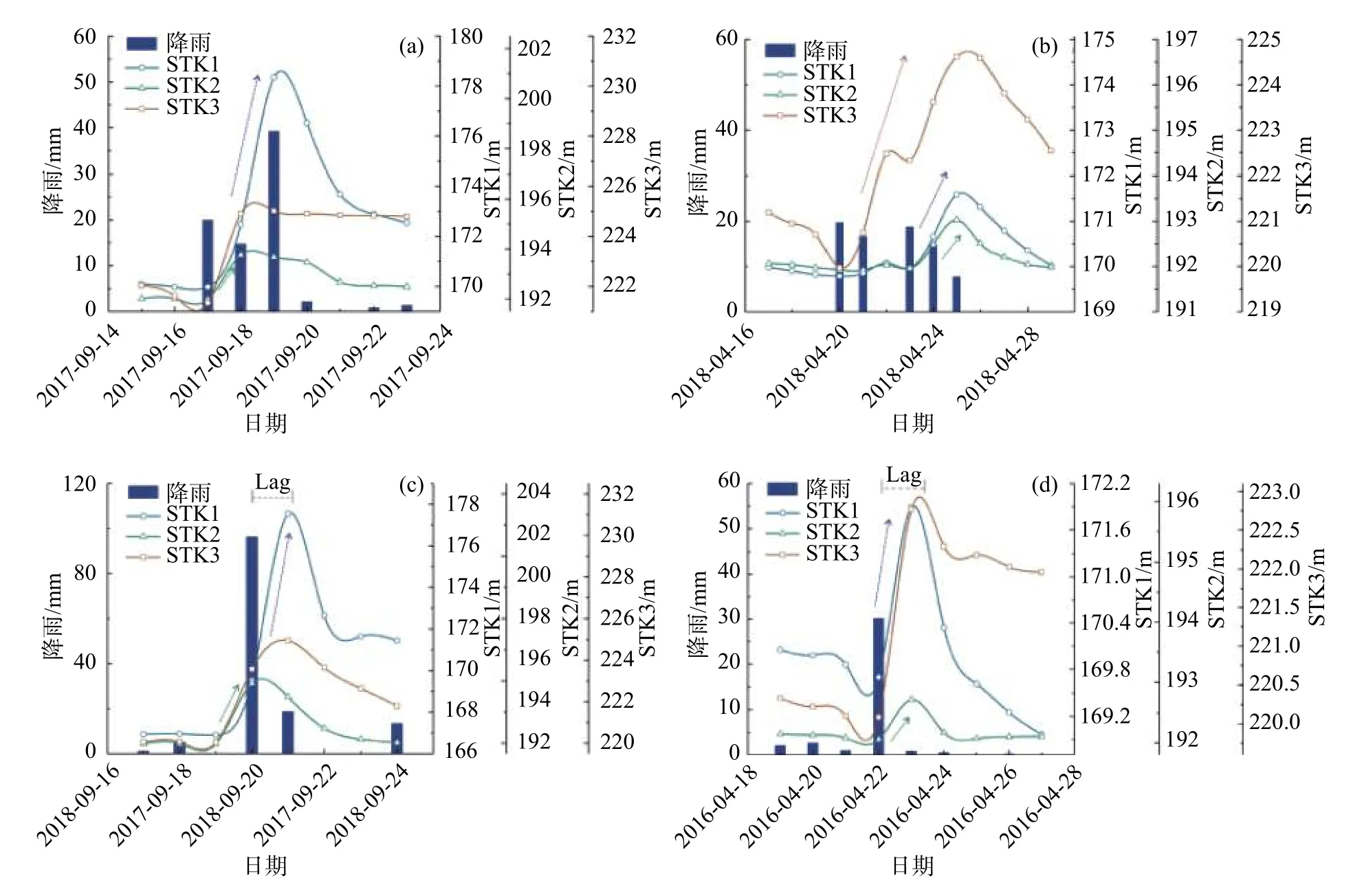
图8 特征降雨时段地下水响应图Fig.8 Groundwater response during the characteristic rainfall period
(2)库水位
为减少降雨因素干扰的影响,在非雨季时期内的低降雨量时间段内分别选取库水位下降和库水位上升阶段进行分析,库水位下降时段地下水位响应情况如图9所示。从图9中可以看出最靠近长江的STK1与库水位相关性较大(关联系数GRI=0.954),水位随着库水位的下降而下降,而位置距离库水较远的STK2和STK3与库水位呈弱相关(GRI分别为0.705和0.689),STK2与STK3位置处的地下水不随库水位的下降而下降,而是保持整体平稳波动。

图9 库水下降时段地下水位响应图Fig.9 The response diagram of groundwater level during the decline period of reservoir water level
库水位上升时段滑坡地下水变动情况如图10所示,与下降期相似,STK1(GRI=0.785)相比于STK2(GRI=0.569)和STK3(GRI=0.568)与库水的关联性更强,与库水位上升趋势保持一致。STK2和STK3在库水位持续升高阶段有数次小幅上升和下降,分析原因是少量降雨补给了地下水后又排泄。

图10 库水上升时段地下水位响应图Fig.10 The response diagram of groundwater level during the rising period of reservoir water level
3.3 地下水水位对库水位和降雨滞后响应
为减少降雨因素的干扰,使用低降雨量时期(2016年12月7日—2017年2月16日)数据求取地下水对库水波动响应滞后期时。首先,对3个水文孔的地下水位数据和库水位数据利用ADF单位根检验其平稳性,检验结果见表1。
第二,小麦中后期管理。自春季以后,小麦便进入到拔节孕穗时期,田间管理应将水肥管理放在前排位置。小麦在拔节前应中耕土壤,长势旺盛高的小麦应进行深度中耕,有效控制小麦的生长情况。在水肥调控上,应及时浇灌长势弱的麦苗,从而提高小麦的数量。在一些土壤条件不好的地方,还需要注意灌溉和施肥情况。当一些土壤条件好的地方,当小麦在返青后,则应控制施肥情况,从而有效调节小麦生长。从而达到抗倒伏的目标。在小麦生长的中后阶段,是防治病虫害的有效时期,要根据值保部门的病虫害情况,采取有效的防治策略。
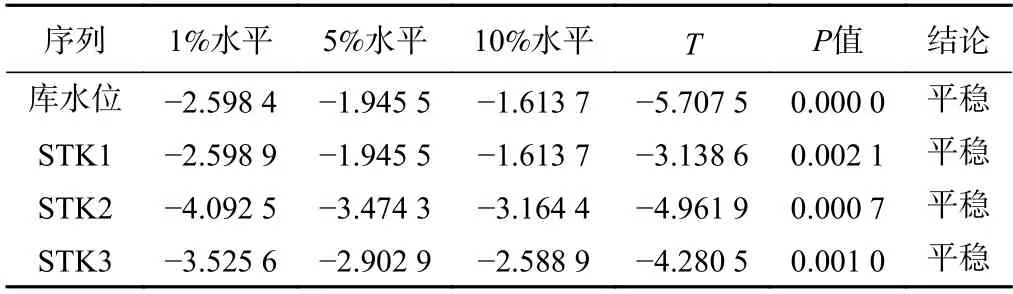
表1 地下水位及库水位平稳性检验结果表Table 1 Stationarity test results of groundwater and reservoir water level
依据表1的统计结果:库水位、STK1、STK2、STK3的T统计量均小于三种置信水平(1%、5%、10%)的临界统计值,同时P值接近于0,拒绝原假设,即各序列均通过平稳性检验。
对上述数据进行Granger因果检验确定最佳的响应滞后期。从表2的结果可以看出,库水位对于STK2和STK3处的地下水位在5%的显著性水平上接受原假设(显著性概率大于5%),即库水位不能很好地解释这两处的地下水变化,而STK1在所设定的滞后期内均能拒绝原假设,表明STK1处的地下水位能与库水位之间表现出较强的因果关系。此外,在滞后期为1~3 d时,显著性概率相比于其他滞后期更接近0,解释效果较好,在滞后期为1 d的时候库水位对于STK1水位的解释效果最好。上述结果表明STK1地下水位孔对库水位的最佳响应滞后期为1 d。
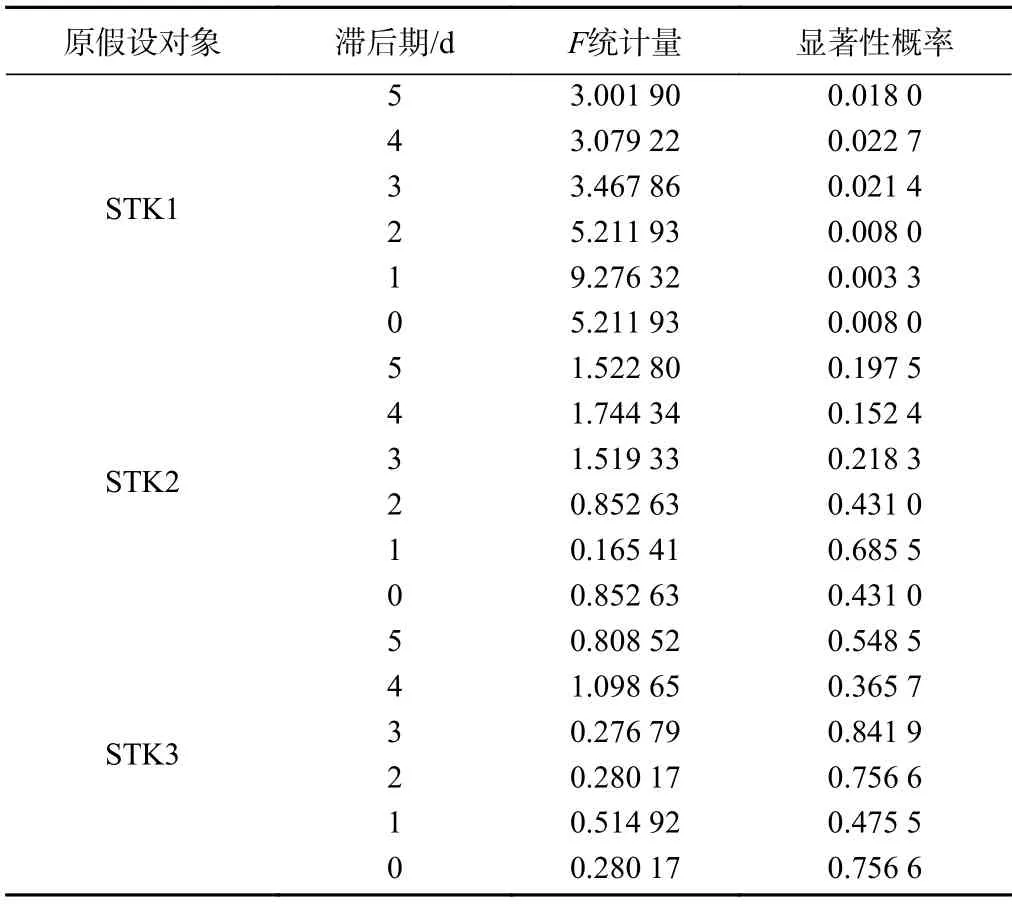
表2 库水位—地下水Granger检验结果Table 2 Granger test results of reservoir water-groundwater
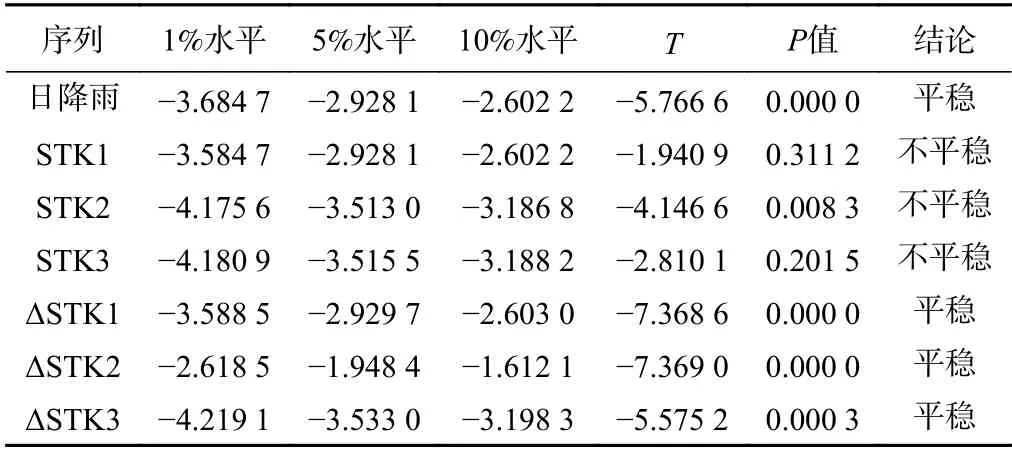
表3 地下水位及降雨平稳性检验结果表Table 3 Stationary test results of rainfall and reservoir water level
对单日降雨量与3个水文孔的地下水位一阶差分数据进行Granger因果检验,检验结果如表4所示。可以看出在滞后期4 d以内,降雨对STK1、STK2、STK3在5%的显著性水平上均能拒绝原假设(显著性概率小于5%),表明在4d内降雨对于滑坡地下水位变动均有一定解释作用,但当滞后期为1 d时显著性概率最低,该结果一定程度上说明麻地湾滑坡地下水位变动对于降雨的最佳响应滞后期为1 d。
基于上述相同的方法分析库水位稳定时段(2017年8月31日—2017年10月15日)地下水对降雨的响应。结果表明三处地下水位监测孔数据均没有通过平稳性检验,需要对其进行一阶差分,一阶差分后的结果(ΔSTK)均通过了平稳性检验,表明一阶差分数据可用于Granger因果检验(表4)。
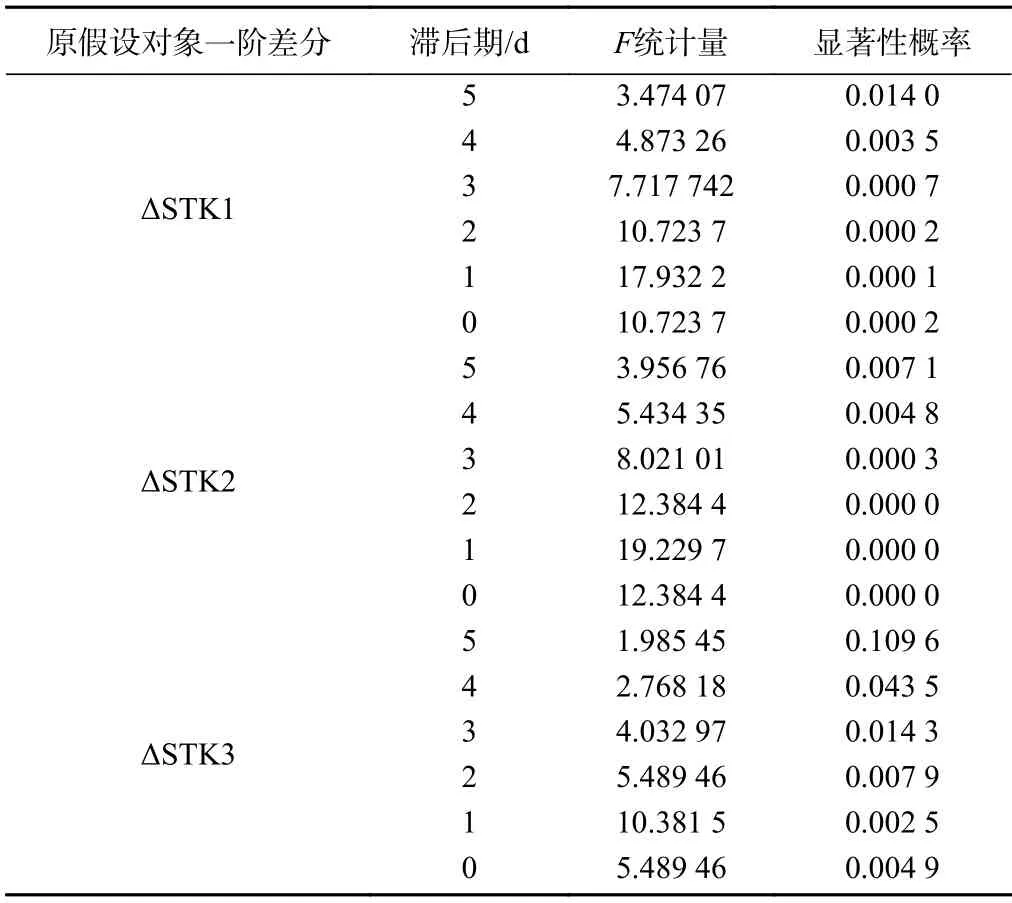
表4 降雨—地下水Granger检验结果Table 4 Granger test results of reservoir water-groundwater
4 库水位及降雨联合影响下地下水响应关联规则挖掘
4.1 地下水变动及影响因素定性分级
在自然情况下,降雨和库水位变动对滑坡稳定性影响是同时存在的,不应单独考虑。本节同时考虑降雨、库水位两个因素,采用关联规则挖掘中的Apriori算法进行麻地湾滑坡地下水响应关联规则挖掘。Apriori算法在进行关联规则挖掘时不能直接对降雨量数据、水位数据等数值型数据进行直接处理,而是要先将数值型数据进行离散化,然后再进行后续处理(图11)。
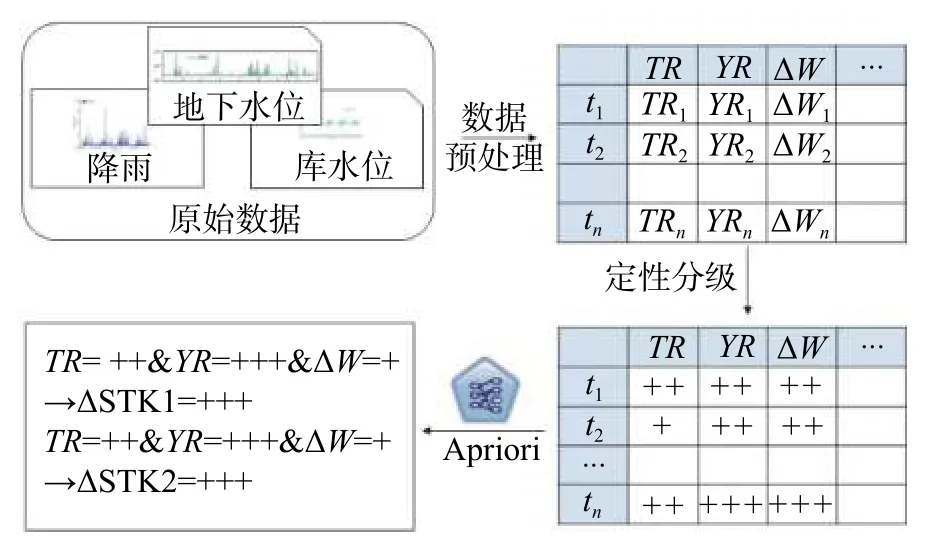
图11 麻地湾滑坡地下水响应关联规则挖掘流程图Fig.11 The flow chart of association rule mining for groundwater fluctuations in Madiwan landslide
(1)降雨量定性分级
依据国家气象局降水强度等级分级标准,结合万州区实际降雨资料将降雨数据划分为小雨、中雨、大雨、暴雨四个等级(表5)。

表5 降雨数据定性分级表Table 5 Qualitative classification table of rainfall
(2)库水位变动定性分级
利用库水位日变动指标,将1 369组库水位变动数据按照“库水位上升状态下的水位变动数据从大到小,库水位下降状态下的水位变动数据从小到大”的原则进行排序。观察数据后发现,不论是上升还是下降状态,数据绝对值的分布特征是“小值集中,大值稀少”。为避免某一区间出现因数据量过大或者过小而造成关联规则挖掘不充分的情况,利用聚类分析算法,将库水日变化按照上升和下降状态各划分快速、中速、慢速三个等级,库水位变动定性分级见表6。

表6 库水位变动数据定性分级表Table 6 Qualitative classification table of reservoir water level fluctuations
(3)地下水位变动等级划分
同样对地下水位按照“上升状态下的水位变动数据从大到小,下降状态下的水位变动数据从小到大”的原则对两组数据进行排序。和库水位相似,地下水位变动绝对值的分布特征同样是是“小值集中,大值稀少”,最后同样利用聚类分析算法,将地下水位变动上升和下降各分快速、中速、慢速三个等级,总共划分六个等级,最终划分等级如表7所示。

表7 地下水变动数据定性分级表Table 7 Qualitative classification table of groundwater fluctuations
由3.3节可知,地下水对降雨和库水的响应会滞后1d,因此关联规则挖掘的前项包含有当日库水位变动(ΔTW)、前一日库水位变动(ΔYW)、当日降雨量(TR)、前一日降雨量(YR)和有效降雨量(RR),有效降雨量依据式(6)计算:
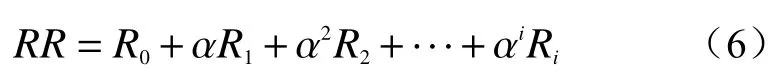
式中:R0——当日降雨;
i——往前第i天的降雨,由于每次降雨实际上只有 部分降雨量对滑坡的发生起作用,所以本处 引入有效降雨量概念,同时前文分析得到麻 地湾滑坡地下水的对降雨最佳响应滞后期为1 d,所以此处i取1;
α——降雨衰减系数,根据前人研究成果,本滑坡所在区域降雨衰减系数为0.8[27]。
4.2 麻地湾滑坡地下水响应关联规则挖掘
将当日库水位变动(ΔTW)、前一日库水位变动(ΔYW)、当日降雨量(TR)、前一日降雨量(YR)和有效降雨量(RR)设置为关联规则挖掘的前项,3个水文孔当日地下水位变化量分别作为后项,产生数据集项共8 817项。将置信度阈值和支持度阈值分别设置为50%和0.5%,建立关联规则挖掘,共有465条有效规则,选取部分规则进行说明(表8)。
各关联规则提升度均大于1,说明前项的发生对于后项的发生具有提升效果,即前项发生时,在一定几率下后项必定发生。表8中,ΔSTK1规则1解释为:当昨日降雨量为小雨,今日降雨量为大雨,昨日库水位为缓慢蓄水时,STK1处的地下水位有80%的概率会缓慢上升,这条规则与3.3节“STK1处地下水对降雨的响应滞后时间为一天”这一结论相符;规则2为:昨日降雨量为大雨,有效降雨量为暴雨,昨日库水位为缓慢下降时,有80%的概率地下水位会快速抬升;规则3为当昨日降雨为大雨,昨日库水位为慢速下降时地下水有80%的概率会中速上升。这三条规则结合起来可以印证位于滑坡下部靠近库水的STK1处的地下水同时受库水位变动和降雨影响。

表8 地下水响应关联规则挖掘列表Table 8 Groundwater response association rule mining result list
ΔSTK2规则1为当有效降雨量为暴雨,当日降雨量为大雨时,地下水位有85.7%的概率会快速上升。ΔSTK3规则1为当昨日降雨为小雨,今日降雨为大雨,今日库水位为缓慢下降,该处地下水位变化位缓慢上升。这桌面滑坡中后缘的STK2、STK3处的地下水对降雨的响应更加强烈。
为方便直观理解和直接运用,采用昨日降雨量和昨日库水位变动两个因子,筛选出最可能出现的情况并绘制地下水响应判别矩阵(表9)。
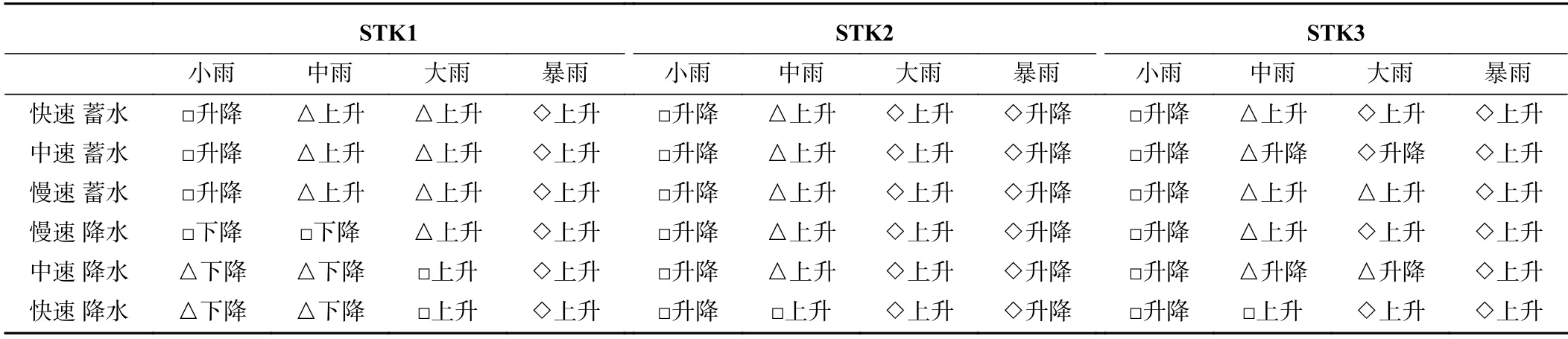
表9 麻地湾滑坡地下水水位响应判别矩阵Table 9 Groundwater level response judgment matrix of Madiwan landslide
由表9可知,在昨日降雨量为中雨以下时,STK1处地下水位变动主要受库水位控制,升降状态与库水位基本保持一致,但当昨日降雨量达到大雨级别,STK1呈中速-慢速上升,当昨日降雨达到暴雨级别,该处地下水将快速升高。STK2处地下水位波动主要受降雨影响,昨日降雨量为小雨时该处地下水水位处于小幅度波动状态;昨日降雨量达到大雨时该处地下水以中等-快速的速度波动,如果昨日降雨量达到暴雨级别,该处地下水位快速上升后往往会伴随地下水水位的快速回落。STK3处地下水位波动主要受降雨影响,在昨日降雨量为小雨时该处地下水水位处于小幅度波动状态,昨日降雨量达到大雨以上级别时能够造成滑坡后缘地下水位的快速上升。
5 结论
本文研究了降雨和库水位变动对麻地湾滑坡地下水水位的影响,并基于数据挖掘算法揭示了麻地湾滑坡地下水水位对降雨和库水位变动的响应规律,取得了到如下结论:
(1)麻地湾滑坡越靠近长江区域的地下水位波动情况与库水位升降的相关性越大,滑坡中部及中后缘对库水位变动的反应较弱。
(2)多日或单日降雨量较高时,麻地湾滑坡前缘地下水位迅速抬升,并且抬升幅度超过其他部位,多日或单日降雨量较小时,滑坡中后缘部位地下水升高相对显著,而滑坡中部地下水的变动幅度始终最小。
(3)通过Granger检验求得STK1对于库水位变动的最佳响应滞后期为1 d。滑坡坡脚处的地下水位变化与降雨的相关性要弱于滑坡的中部及中后缘,所研究3处水文孔水位对降雨的最佳响应滞后期为1 d。
(4)Apriori算法关联规则挖掘结果显示:滑坡前缘STK1处地下水波动同时受到降雨和库水位的影响,位于滑坡中后缘的STK2、STK3处的地下水对降雨的响应更加强烈。所挖掘的关联规则对于后项的提升效果较好,规则置信度较高,借助响应判别矩阵能够短时预测地下水位变动情况。
(5)研究麻地湾滑坡地下水对库水和降雨的响特征可以为地质背景条件相似的库岸滑坡的预警预报增加理论依据。基于本文研究,在对该类边坡进行工程治理时,可考虑后缘截设置排水沟削弱降雨影响,而前缘修建相应防水工程,减弱库水位影响。
——以连云港市为例

