北斗卫星广播星历精度评估与单点定位优化模型
简濠骏 王逸石 张元泰 魏英韬 周裕欣
1 武汉大学测绘学院,武汉市珞喻路129号,430079
北斗卫星导航系统(BDS)是中国研发的全球卫星导航系统,其发展包括3个阶段:示范导航卫星系统(BDS-1)、区域导航卫星系统(BDS-2)和全球北斗导航系统(BDS-3)。目前,BDS发展趋势持续向好,与其相关的产业和服务在全球发展迅速,在全球定位、导航和授时PNT中发挥了重要作用[1]。BDS星座由3种轨道类型的卫星组成,分别为地球静止轨道GEO卫星、倾斜地球同步轨道IGSO卫星和中地球轨道MEO卫星。截至2020-07,BDS在轨卫星由15颗BDS-2卫星和30颗BDS-3卫星组成,并且大多数BDS-2卫星在轨时钟处于最后阶段,因此评估卫星时钟和星历性能至关重要[2]。BDS-3卫星星座已开始提供全球服务,评估BDS-3广播星历轨道和钟差精度,依据评估结果进一步对单点定位定权,是分析和提高单点定位精度的关键。
随着BDS-3的发展,全球平均可见卫星数从5.1颗增加到10.7颗[3]。同时,BDS-2 SISRE的平均均方根RMS和标准差STD分别为1.78 m和0.40 m,若只考虑轨道影响,则分别为1.72 m和0.34 m。BDS-3 SISRE的平均RMS和STD分别为0.50 m和0.14 m,若只考虑轨道影响,则分别为0.17 m和0.04 m[4]。 BDS-3轨道在径向、沿轨和跨轨方向的精度分别为0.07 m、0.30 m和0.26 m。就SISRE而言,若仅考虑轨道影响,则BDS-3平均SISREorb为0.08 m;若综合考虑轨道和钟差,则BDS-3 SISRE平均值约为0.50 m[5-6]。同时,BDS-2 MEO卫星SISRE平均值约为1.0 m[7]。在卫星钟方面,BDS-3卫星能够配备高精度的新型Rb钟和 H钟[8-9]。
本文主要对BDS-2和BDS-3广播星历的轨道及钟差精度进行系统评估,并进一步比较分析不同BDS-2和BDS-3卫星星座组合对单点定位的影响。最后,利用星历评估的SISRE,提出并验证SPP加权优化模型,进一步分析不同时长的SISRE对模型优化结果的影响。
1 精度评估原理
在进行广播星历评估时,利用武汉大学的精密星历产品作为真值,具体流程如图1所示。表1为目前BDS的星座构成。自2021年起,广播星历开始播发C38~C46卫星的轨道根数,其中C38、C39和C40为BDS-3的IGSO卫星,而C41~C46为BDS-3的MEO卫星,两者的时钟类型均为H钟。
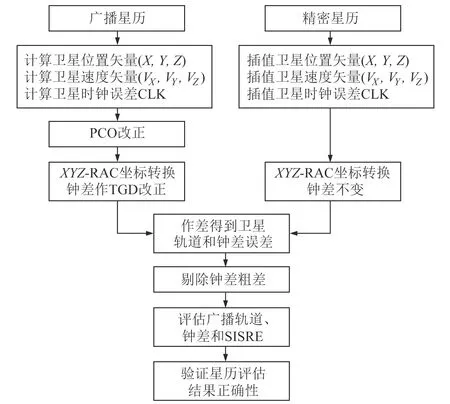
图1 广播星历评估流程Fig.1 The process of broadcasting ephemeris evaluation
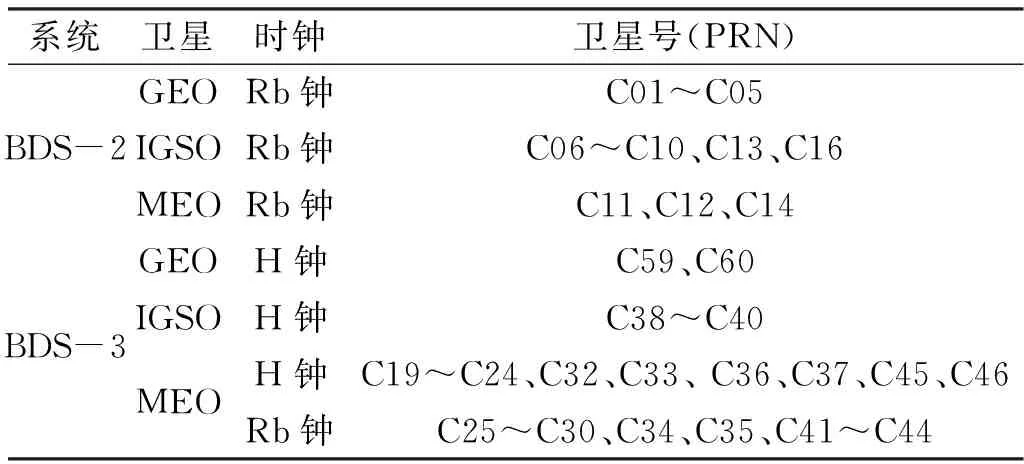
表1 BDS星座构成
1.1 卫星轨道及钟差计算
BDS广播星历提供16个参数,包括1个参考时刻、6个参考时刻处的开普勒轨道参数和9个轨道扰动项参数。 接口文件[10-11]中已详细描述BDS的MEO、IGSO和GEO卫星广播星历算法。
1.2 参考框架差异
BDS卫星广播轨道基于北斗坐标系(Beidou coordinate system, BDCS),而精密轨道基于国际地球参考框架(international terrestrial reference frame, ITRF),两者间差异仅为4 cm[12],与广播轨道精度相比可忽略不计。因此,评估时可忽略两个框架之间的差异。
1.3 天线相位偏移
精密星历提供的卫星轨道参考点为卫星质心(COM),而广播星历提供的轨道参考点在天线相位中心(APC)。从2017-01-07开始,BDS轨道参考点由COM更改为APC,与其他GNSS系统相同。广播星历中使用的天线相位中心偏移(PCO)由中国卫星导航办公室测试评估研究中心提供。实际计算时还需考虑太阳位置等因素,将PCO转换到地心地固坐标系下。
1.4 群延迟改正
广播星历和精密星历之间的钟差差异为系统偏差。BDS广播钟差基于B3频点,而精密钟差基于B1和B3频点。为统一时间基准,在评估广播星历钟差精度时需要进行改正处理:
(1)
式中,f1、f3分别为B1和B3频点的频率,tB3为广播钟差,TGD1为广播星历群延迟参数[4]。
本文使用“双差法”处理BDS广播钟差,即采用星历钟差与其单日均值之差来消除时钟系统偏差,然后再计算广播钟差与精密钟差的差异。
1.5 粗差剔除
本文首先排除不健康的星历,避免广播星历的错误参数对评估结果造成影响。此外,采用中位数法对钟差粗差进行剔除[13],其表达式为:
(2)
式中,M为整个钟差时间序列XCLK的中位数;Mdian为计算中位数的函数;当|Xi|>M+nMad时则认为是粗差,其中n取5。
1.6 SISRE模型
SISRE是评估广播星历精度的常用量。针对BDS,SISRE的表达式为[7]:
(3)
式中,R、A和C分别为径向、沿轨和跨轨方向轨道误差,c为光速,T为钟差,ω1和ω2是与星座相关的权重因子。对MEO卫星,ω1为0.963 1,ω2为0.018 4;对于IGSO和GEO卫星,ω1为0.984 2,ω2为0.007 9。忽略钟差影响,SISREorbit可表示为:
(4)
2 广播星历精度分析
实验数据采用IGN机构发布的2021年年积日001~091连续广播星历和精密星历。根据广播星历计算卫星轨道和钟差,再与精密星历内插的精确结果作差得到广播星历轨道误差和钟差时间序列,统计三维误差和SISRE。同类型卫星的各项指标类似,故选取单颗各类卫星对比分析。为凸显周期性变化,仅绘制7 d的统计时间序列,而统计RMS值时采用91 d结果。
2.1 BDS-2卫星广播星历精度分析
图2为BDS-2 GEO、IGSO和MEO卫星广播星历轨道误差在7 d内各方向及三维统计的时间序列。从图中可以看出,对于轨道分量,BDS-2卫星轨道R方向精度优于A、C方向,且在A、C方向上MEO和IGSO卫星精度优于GEO卫星,A、C方向精度可能与轨道高度有关,轨道高度越低精度越差;对于三维误差,MEO卫星的三维误差优于IGSO和GEO卫星,IGSO和GEO卫星在A、C方向的轨道误差分量具有明显的周期性,而MEO卫星周期性不明显,这可能与其轨道类型有关。
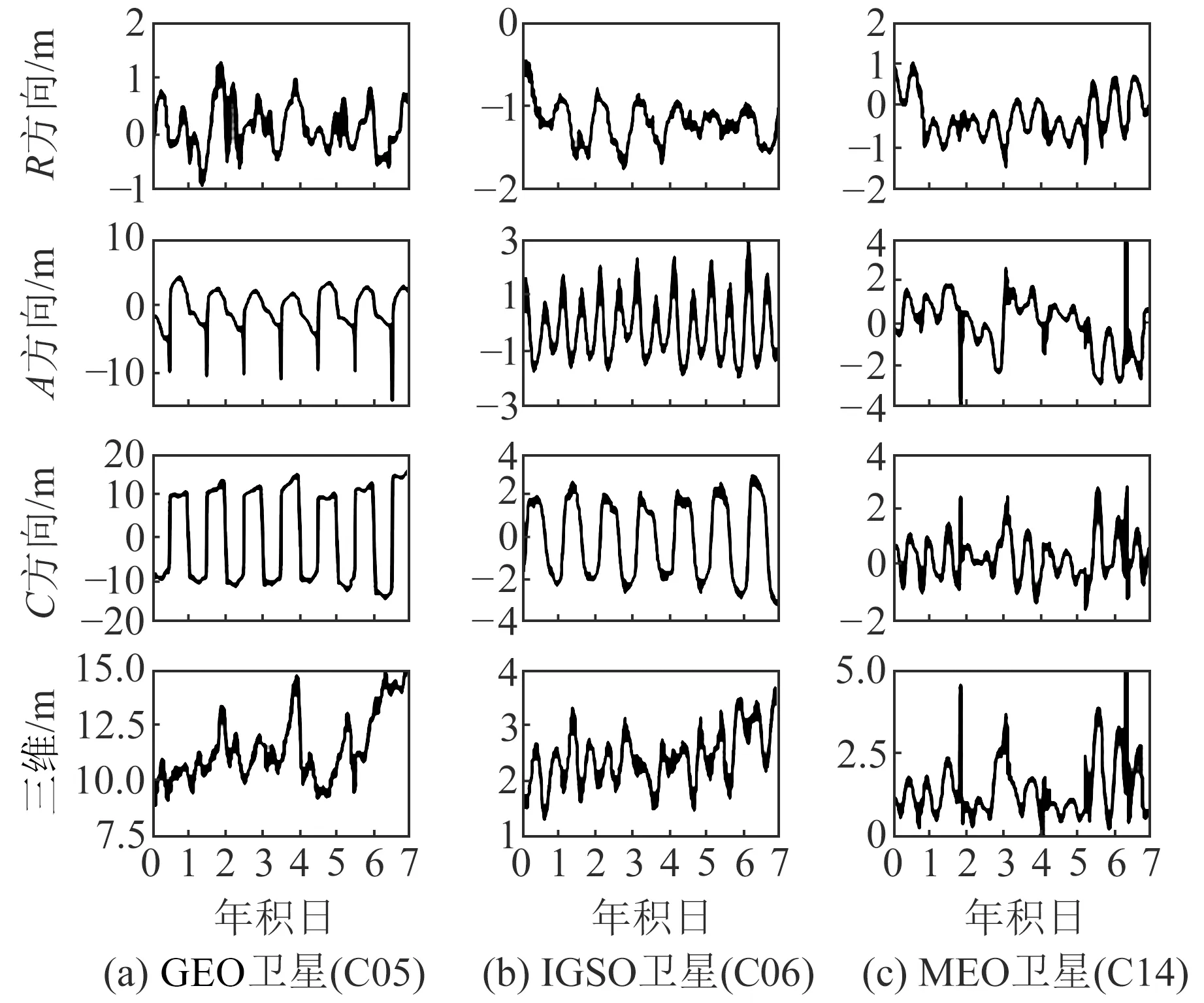
图2 BDS-2卫星结果(1~7 d)Fig.2 BDS-2 satellite results (1~7 d)
2.2 BDS-2与BDS-3广播星历精度对比分析
图3为BDS-2和BDS-3 IGSO卫星广播星历轨道误差在7 d内各方向及三维统计的时间序列。可以看出,BDS-3 IGSO卫星轨道在A、C方向的误差也具有周期性。对于轨道分量,BDS-3 IGSO卫星在R、A、C三个方向的精度均明显优于BDS-2;对于三维误差,BDS-3 IGSO卫星也明显优于BDS-2。图4和图5分别为BDS-2和BDS-3各颗卫星按91 d统计的STD值。从图中可以看出,相较于BDS-2,BDS-3 各项结果变化更为平稳,其R、A、C方向的轨道误差分量、钟差和三维轨道误差的标准差均在1 m以内。
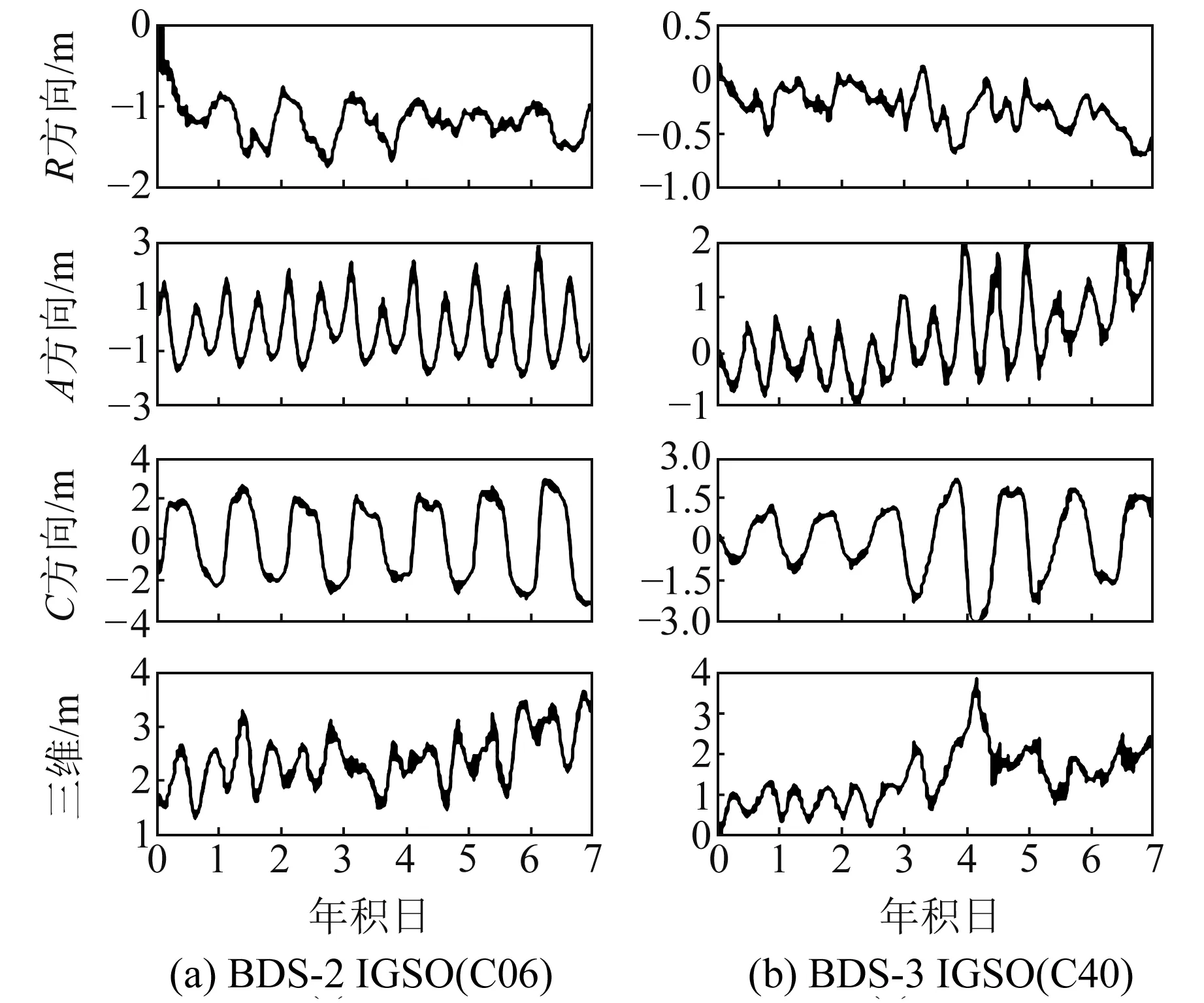
图3 IGSO卫星结果对比(1~7 d)Fig.3 Comparison of IGSO satellite results (1~7 d)
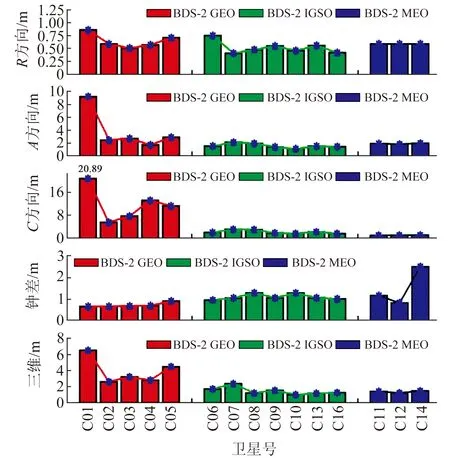
图4 BDS-2各颗卫星结果标准差Fig.4 STD of results for BDS-2 satellites
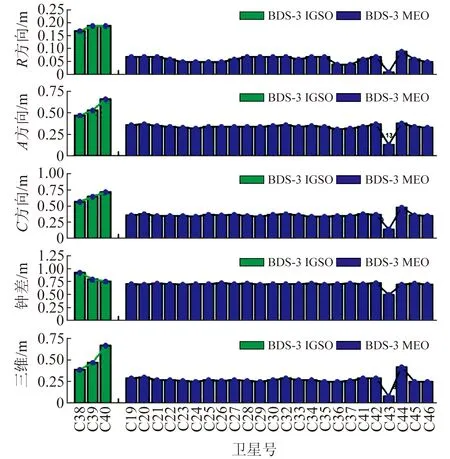
图5 BDS-3各颗卫星结果标准差Fig.5 STD of results for BDS-3 satellites
图6为BDS-2和BDS-3 MEO卫星广播星历轨道误差在7 d内各方向及三维统计的时间序列。从图中可以看出,对于轨道分量,BDS-3 MEO卫星在R、A、C三个方向的精度及三维轨道误差均明显优于BDS-2;BDS-3 MEO卫星R方向的轨道误差具有周期性,且周期短于BDS-2 IGSO、GEO卫星。结合图4和图5可知,相较于BDS-2 MEO卫星,BDS-3各项结果变化更加平稳,其R、A、C方向的轨道误差分量、钟差和三维轨道误差的STD均值都优于0.75 m。
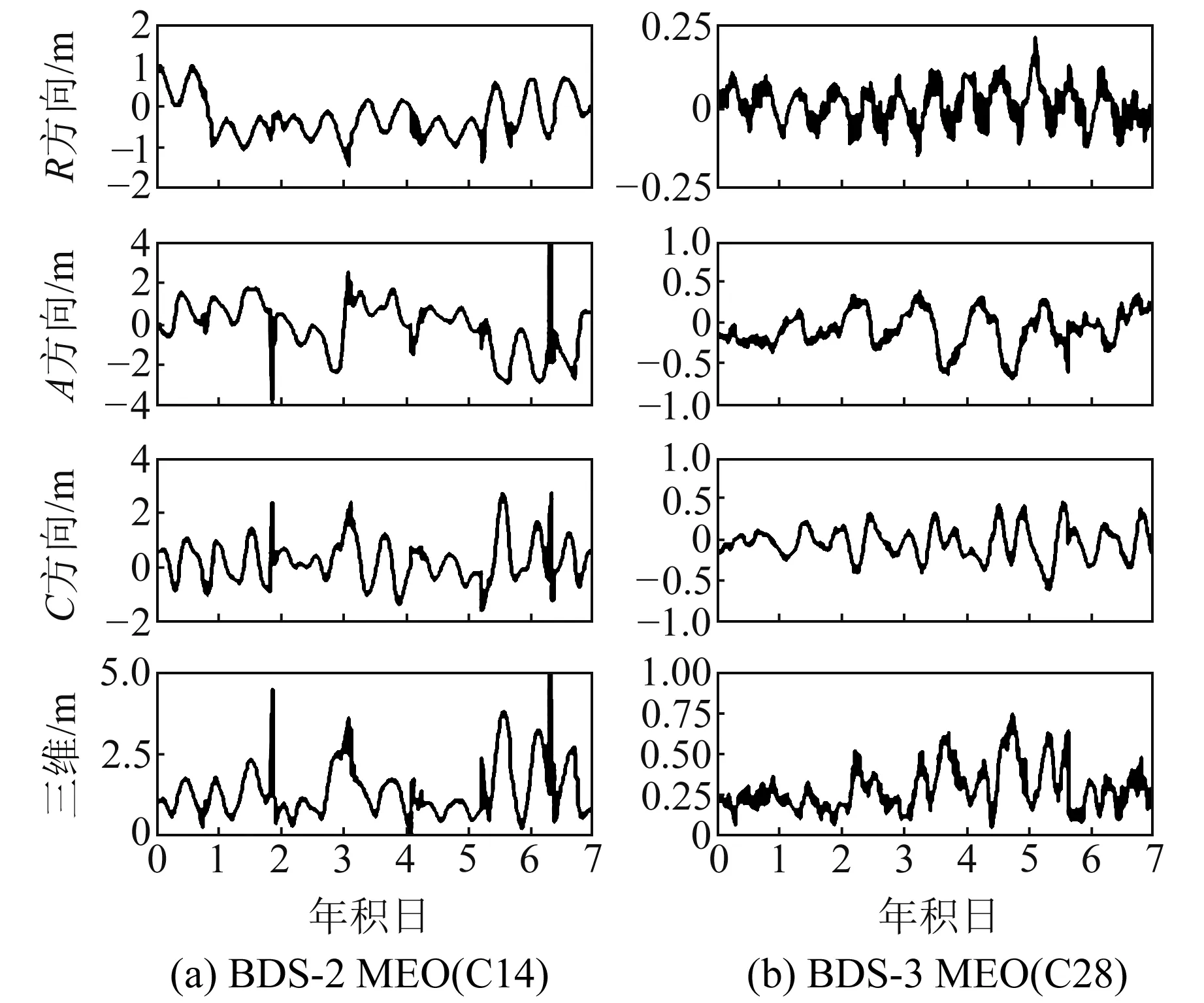
图6 MEO卫星结果对比(1~7 d)Fig.6 Comparison of MEO satellite results (1~7 d)
图7和图8分别为BDS-2和BDS-3各颗卫星结果按91 d统计的RMS值。从图7可以看出,对于BDS-2,MEO卫星三维轨道误差优于IGSO和GEO卫星,其RMS约为2.4 m;IGSO卫星次之,其三维轨道误差在3.0 m左右;而GEO卫星除C01三维轨道误差在20 m左右,其他4颗GEO卫星的轨道误差也基本在7 m以上。结合表2可知,钟差精度由高到低排序依次为GEO、IGSO、MEO,三者SISRE精度在同一水平。
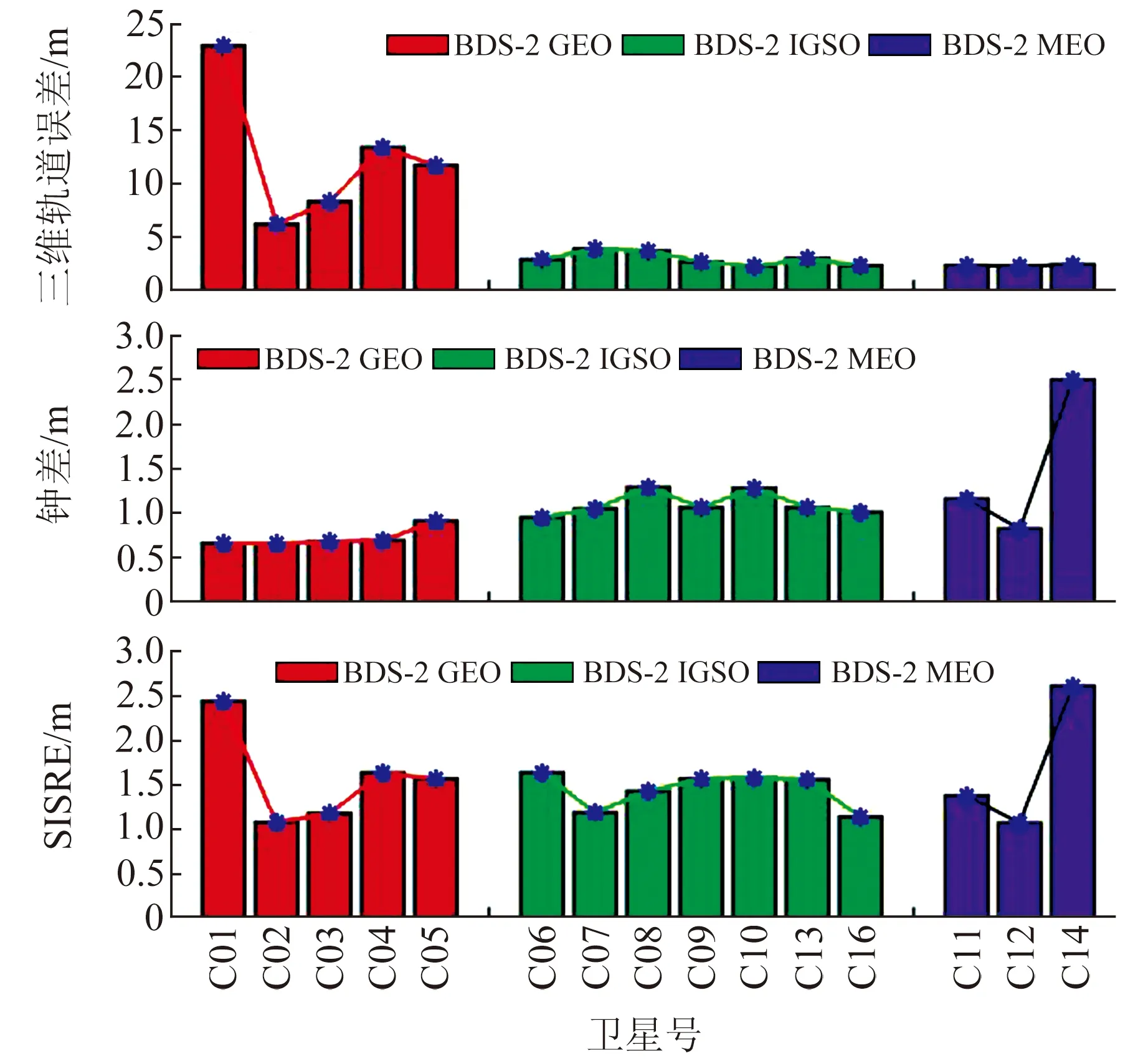
图7 BDS-2卫星三维轨道误差、钟差和SISRE的RMS(1~91 d)Fig.7 RMS of BDS-2 satellite 3D orbit error, clock error and SISRE (1~91 d)
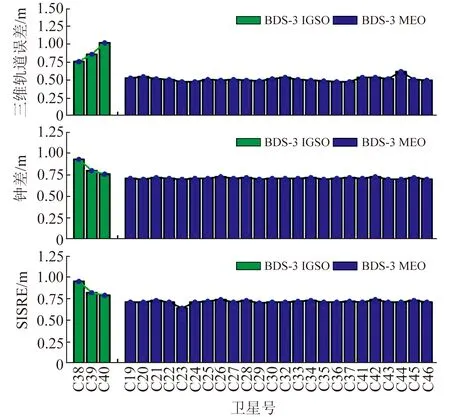
图8 BDS-3卫星三维轨道误差、钟差和SISRE的RMS(1~91 d)Fig.8 RMS of BDS-3 satellite 3D orbit error, clock error and SISRE (1~91 d)
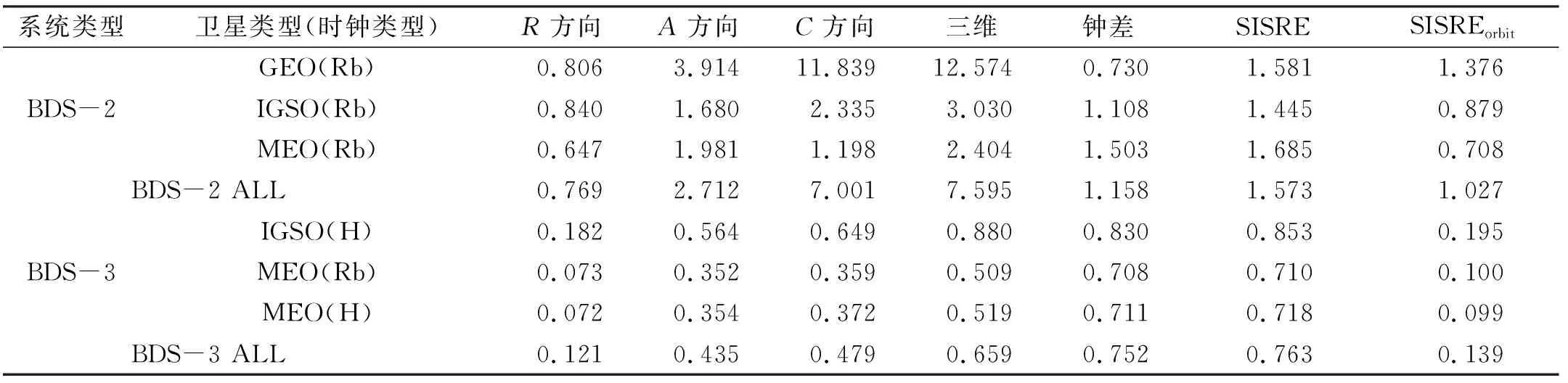
表2 1~91 d各类卫星各项指标统计结果(RMS)
从图8可以看出,BDS-3的三维轨道误差明显优于BDS-2,其各颗IGSO卫星的三维轨道误差均在1 m左右,MEO卫星的三维轨道误差在0.7 m以内;对于钟差,BDS-3 IGSO和MEO各颗卫星均优于BDS-2同类卫星,其RMS分别在0.8 m和0.7 m左右;对于SISRE,BDS-3各颗卫星均优于BDS-2,其中IGSO卫星的RMS在0.95 m以内,MEO卫星的RMS在0.75 m以内。
表2(单位m)为各类卫星各项指标按91 d统计的RMS值。从表中可以看出,BSD-3 MEO卫星和IGSO卫星的轨道误差、钟差、SISRE均优于BDS-2同类卫星。此外,结合图5和图8可知,BDS-3 MEO卫星配备H钟和Rb钟的钟差差异很小。
3 单点定位结果验证及精度分析
在单位权模型的伪距单点定位中,广播星历误差是定位误差的主要来源之一。为验证星历评估结果的正确性,本文采用BDS-2/BDS-3 IGSO/MEO星座组合,选取6个IGS站2021年年积日001~007的连续数据进行SPP解算。在具体解算时,使用B1I与B3I频点组成消电离层组合观测值:
(5)
通过最小二乘法进行解算,以SINEX文件作为坐标真值,对定位误差进行统计(图9)。根据表1中BDS星座构成,研究5种不同星座组合对SPP结果的影响,5种组合分别为BDS-2 IGSO/MEO组合(组合1)、BDS-3 MEO组合(组合2)、BDS-3 IGSO/MEO组合(组合3)、BDS-2/BDS-3 MEO组合(组合4)、BDS-2/BDS-3 IGSO/MEO组合(组合5)。利用2021年年积日001~007的数据解算ALIC等12个IGS站SPP结果,统计N、E、U方向的RMS值(图10)。
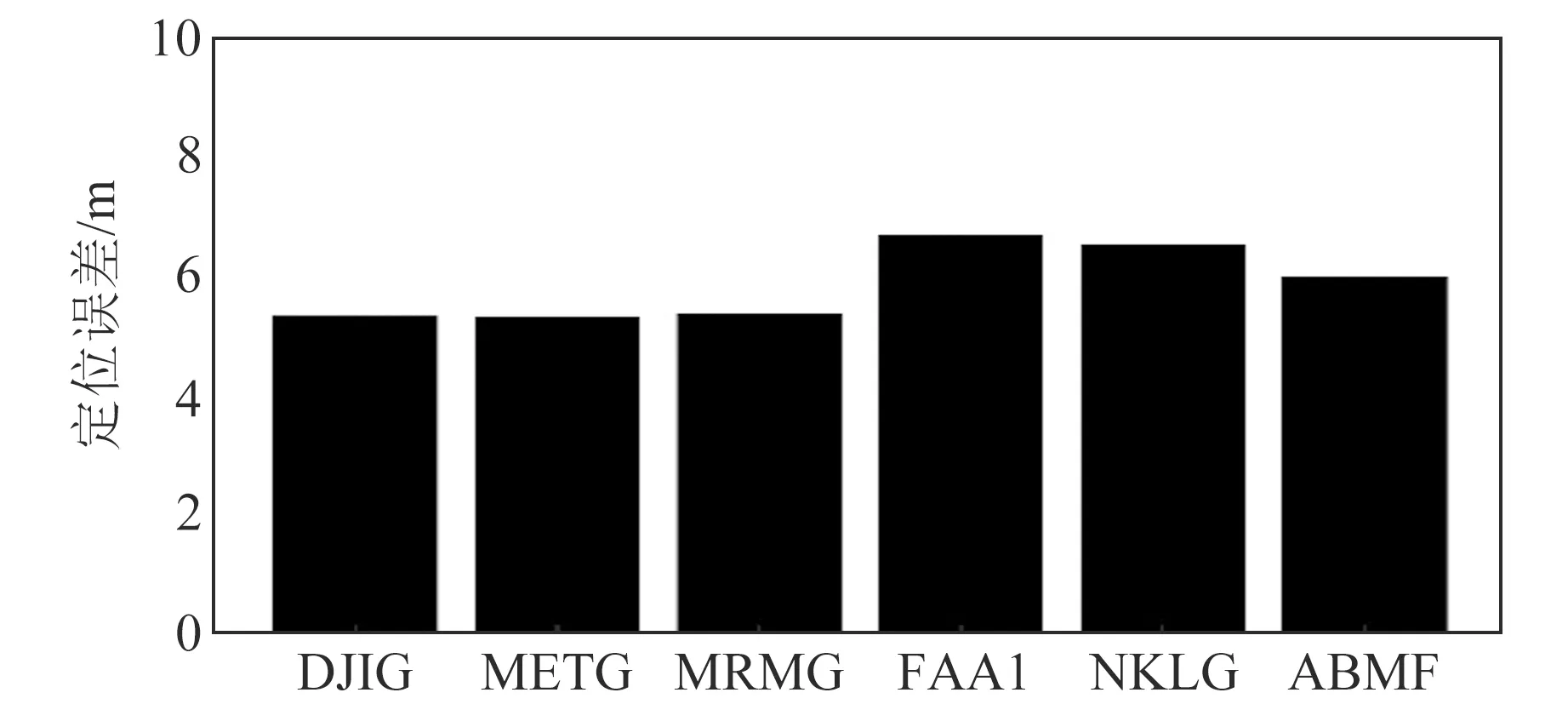
图9 6个观测站1周单点定位结果(RMS)Fig.9 SPP results (RMS) of six stations in one week
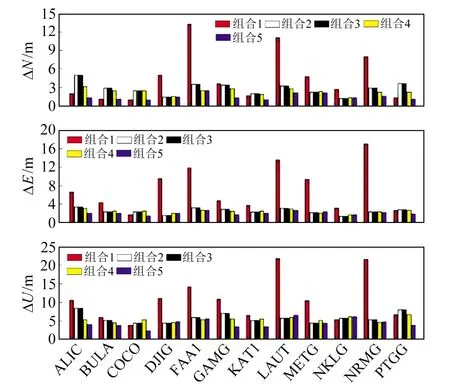
图10 不同星座组合SPP结果(RMS)Fig.10 SPP results (RMS) of different constellation combinations
由图9可见,SPP各方向精度均在m级,且三维误差约为5 m,符合预期精度,从而验证了星历评估的正确性。由图10可见,BDS-2/BDS-3 IGSO/MEO星座组合定位各方向结果均优于其他星座组合,各方向精度基本在3~4 m;BDS-2 IGSO/MEO星座组合定位结果最差。因此,在解算SPP时,选择BDS-2/BDS-3 IGSO/MEO星座组合最佳。
4 伪距单点定位SISRE加权模型
在前文基础上,本文提出一种基于广播星历质量的伪距单点定位加权方法,以抑制广播星历误差对定位结果的影响。在评估得到各卫星的SISRE后,将其平方的倒数设为对应伪距观测值的权值:
(6)
式中,i为卫星PRN号,Pi为解算时的卫星权值。
4.1 模型检验
为验证模型的优化效果,本文采用BDS-2/BDS-3 IGSO/MEO星座组合进行单点定位解算。其中,式(6)的SISRE由星历评估得到,具体值见图7和图8。分析ABMF等7个IGS站的单位权与SISRE定权的定位精度,统计N、E、U方向的RMS值(图11、表3)。从图11和表3可以看出,SISRE加权优化模型可提高SPP各方向的定位精度,在N、E、U方向上的平均优化率分别为9.61%、18.55%、11.19%,平均总体优化率达到12.26%。
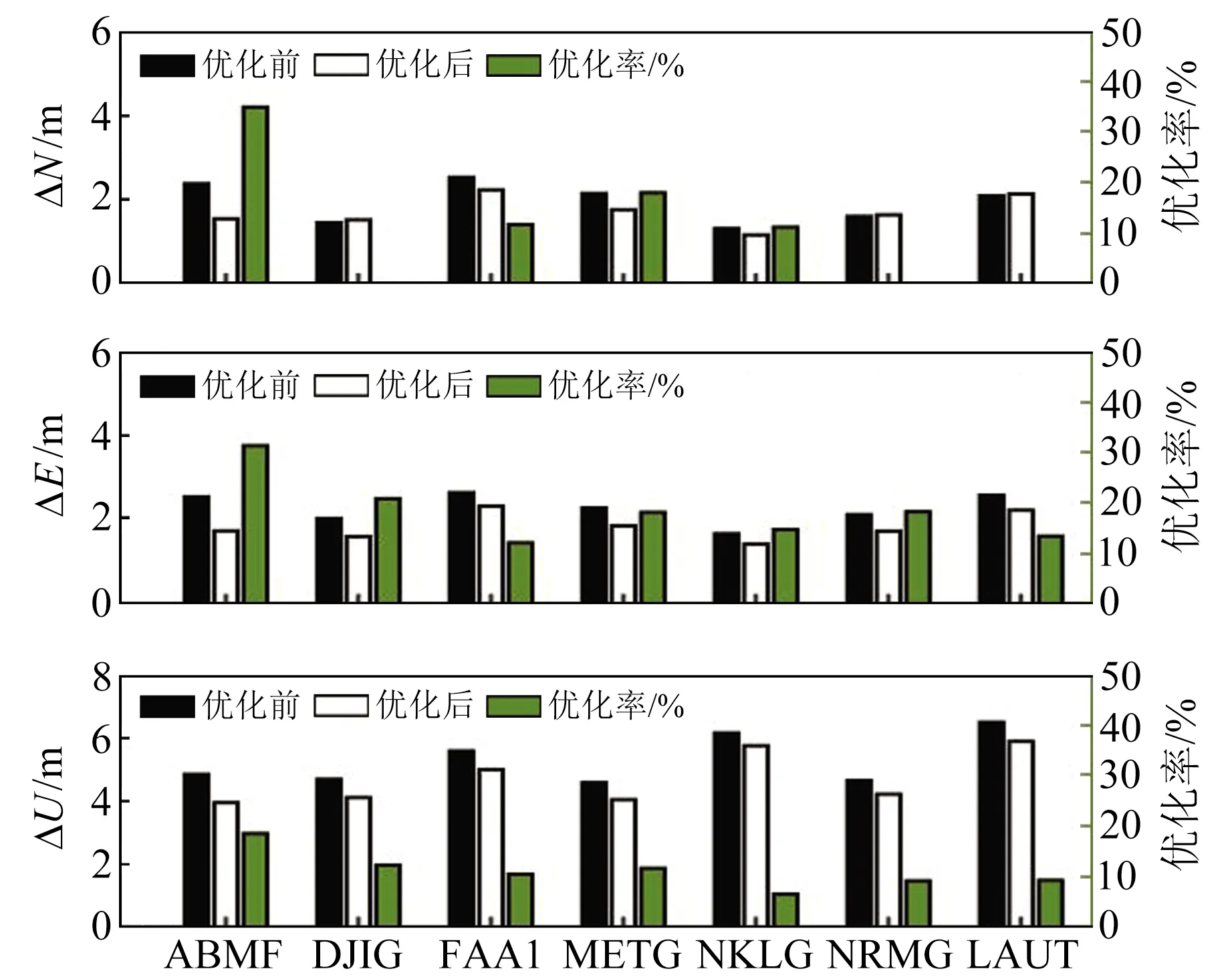
图11 1周单点定位结果(RMS)优化对比Fig.11 Optimization comparison of SPP results (RMS) in one week
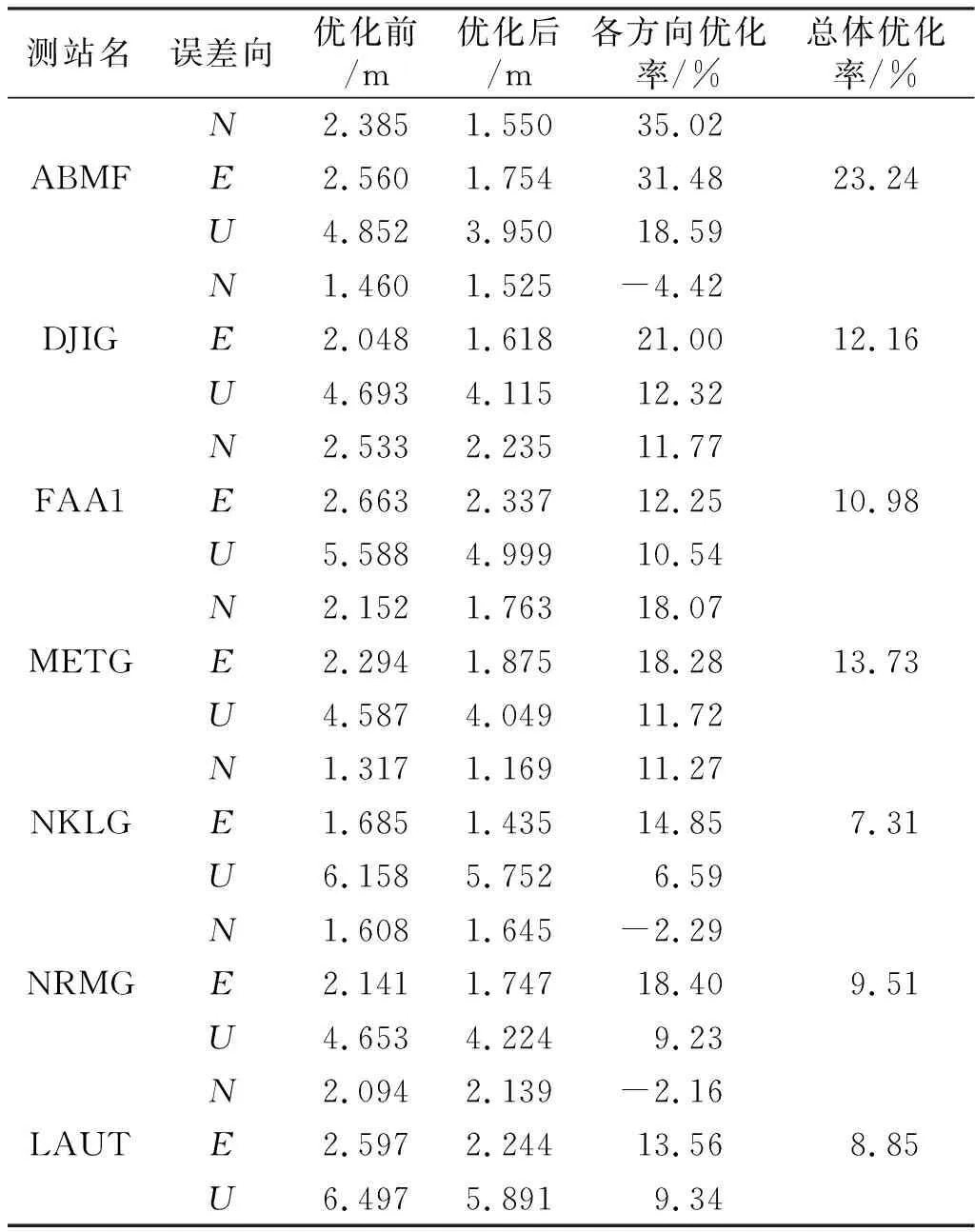
表3 优化前后SPP结果(RMS)
4.2 模型分析
为检验SISRE平均时长对模型优化效果的影响,进一步对同期(7 d)、短期(1个月)、中期(2个月)、长期(3个月)4组不同时长得到的平均SISRE进行对比分析。按照§4.1中星座组合及解算方法,对ABMF等7个站2021年年积日001~007的数据进行SPP解算,统计结果如图12和表4所示。
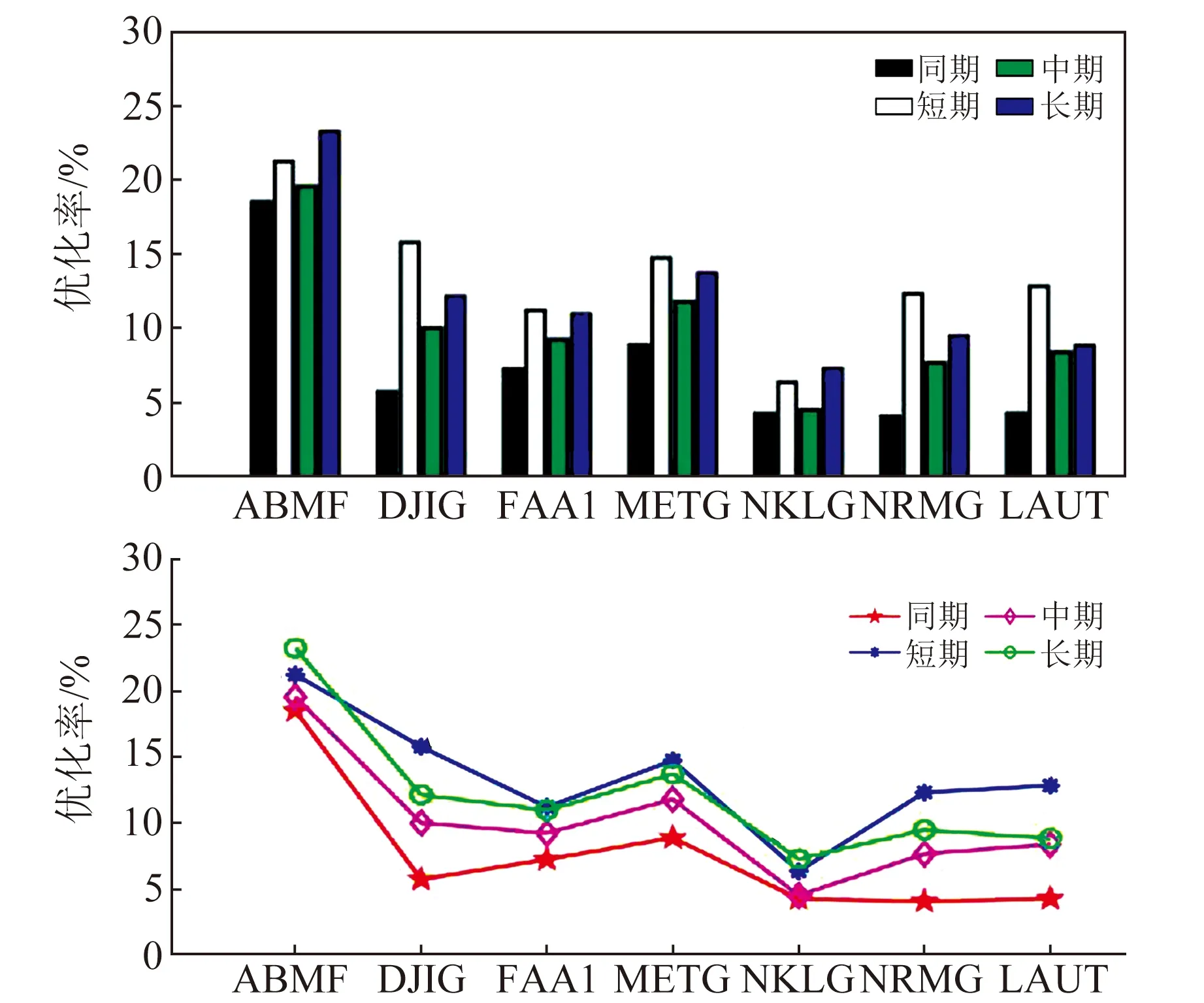
图12 不同时长SISRE对单点定位结果(RMS)的优化对比Fig.12 Optimization comparison of SPP results (RMS) with different SISRE
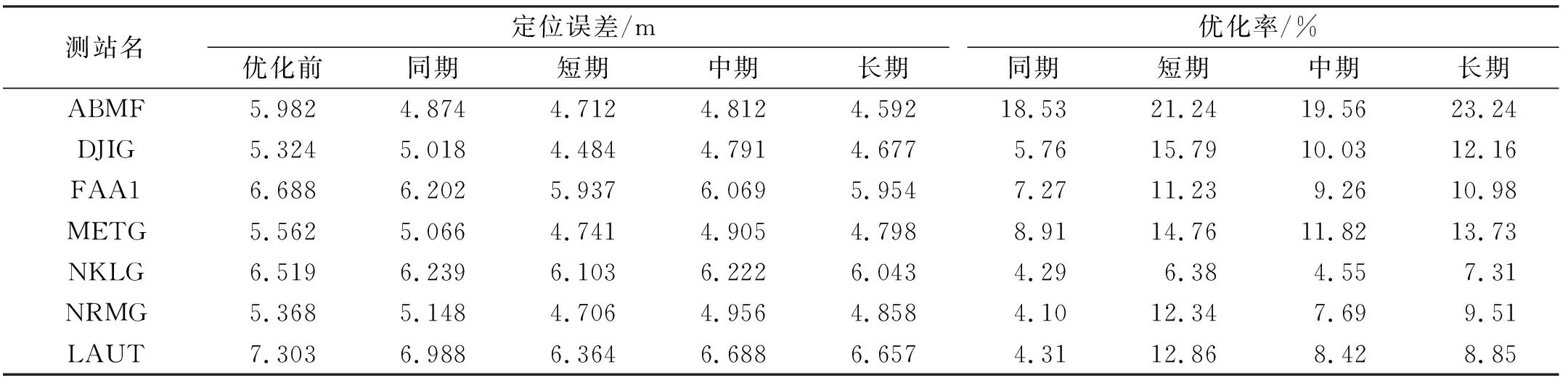
表4 不同时长SISRE对单点定位结果(RMS)的优化对比
5 结 语
本文使用精密星历评估BDS-2和BDS-3卫星广播星历的精度,并进一步研究不同星座组合对单点定位结果的影响,提出一种基于广播星历精度的SISRE加权模型,得到以下结论:
图12为不同时长SISRE对单点定位结果(RMS)的优化情况。从图中可以看出,采用同期时长的优化效果最差,短期时长的优化效果最优,而中期和长期时长的优化效果介于两者之间。这可能是因为7 d同期的SISRE结果不足以充分体现卫星广播星历的质量,而时长过长又会引入时间间隔过久的星历数据,对当前时间段的SPP产生一定程度的干扰。因此,选取时长为1个月的短期SISRE效果最佳。在具体解算时,SISRE最佳平均时长的选择还需进一步研究。
1)BDS-2中MEO卫星广播星历精度优于IGSO和GEO卫星;GEO卫星轨道的RMS最差约为12 m,IGSO和MEO卫星轨道的RMS均在2~3 m左右;BDS-2卫星的SISRE平均优于2 m。
2)BDS-3的三维轨道误差和SISRE均优于BDS-2,两者均在1 m以下;BDS-3卫星的钟差优于BDS-2,这可能与BDS-3新增的星间链路有关[14],而BDS-3中配备H钟的MEO、IGSO卫星与配备Rb钟的同类卫星的钟差及其标准差基本相同。
3)利用12个IGS站2021年年积日001~007的数据进行单点定位解算,比较不同星座组合的SPP定位精度,结果显示,BDS-2/BDS-3 IGSO/MEO星座组合精度最高。
4)对SISRE加权单点定位模型的优化效果进行验证。结果表明,相比于单位权模型,SISRE加权模型的定位精度在N、E、U方向的平均优化率分别为9.61%、18.55%、11.19%,平均总体优化率达12.26%。
5)分析SISRE平均时长对模型优化效果的影响可以发现,采用同期时长的优化效果最差,短期时长的优化效果最优,而中期和长期时长的优化效果介于两者之间。其原因可能是7 d同期的SISRE结果不足以充分体现卫星广播星历的质量,而时长过长又会引入时间间隔过久的星历数据,对当前时间段的SPP产生一定的干扰。因此,选取时长为1个月的短期SISRE效果最佳。

