TDOA定位精度分析
芦伟东
(国家无线电监测中心哈尔滨监测站,黑龙江 哈尔滨 150010)
0 引言
到达时间差(TDOA)无源定位技术是根据目标辐射源发射的射频信号到达不同监测站的时间差进行目标源定位的一种技术[1]。TDOA定位技术不要求目标辐射源与各监测站时间同步,但必须保证各监测站间时间完全同步。由于TDOA定位技术具备系统复杂度低、定位精度较高和监测站之间的距离不受限制等优点[2],其已在无线电频谱管理领域得到广泛应用。本文主要研究了TDOA的定位原理,分析不同因素对定位精度和有效定位范围的影响,为今后的无线电监测定位工作提供参考建议。
1 TDOA定位基本原理
TDOA定位原理是基于双曲线的定义:一个平面上与两个固定点(称为焦点)的距离差的绝对值是常数的点的轨迹。在无线电监测定位中,无线电信号的传播速度等于光速,目标辐射源到两个监测站的距离差等于光速与到达时间差的乘积,所以目标辐射源的运动轨迹就是以监测站为焦点的双曲线[1],[3]。如图1所示。
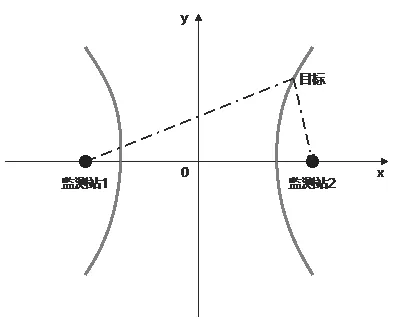
图1 TDOA定位原理示意图
为了定位目标辐射源,只有一条双曲线还不够,在平面内需要至少三个监测站才能得到两条双曲线,从而实现定位目标辐射源。定位示意图如图2所示。
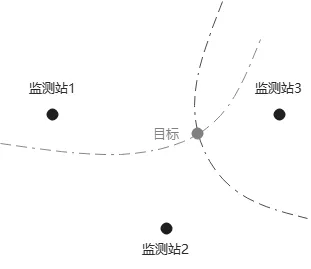
图2 三站定位示意图
对于多站定位的情[4-6],假设TDOA定位系统由M+1个监测站组成,其中主监测站为S0,M个辅监测站,各监测站坐标为(xi,yi,zi),i=0,1,2…,M。设目
标辐射源T(x,y,z)发出的无线电信号到达各监测站
的时间为ti(i=0,1,2,…,M),到达各监测站的距离为ri(i=0,1,2,…,M),则T到达第i个辅监测站与到达主监
测站的距离差为
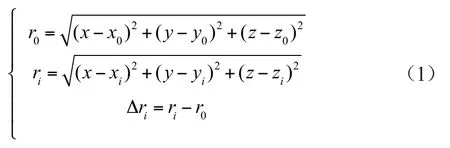
对式(1)化简,得到
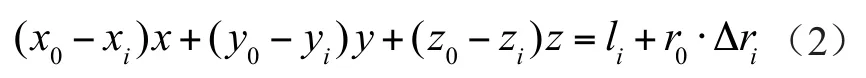
式中,li为
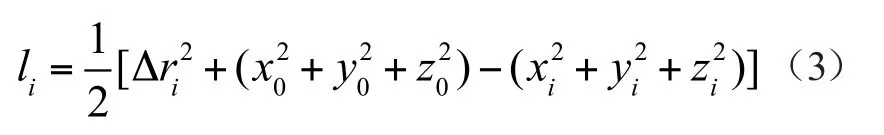
式(2)表示共有i=1,2,…,M个的方程构成了一个非线性方程组,矩阵形式可表示为

式中,A,X,B分别为
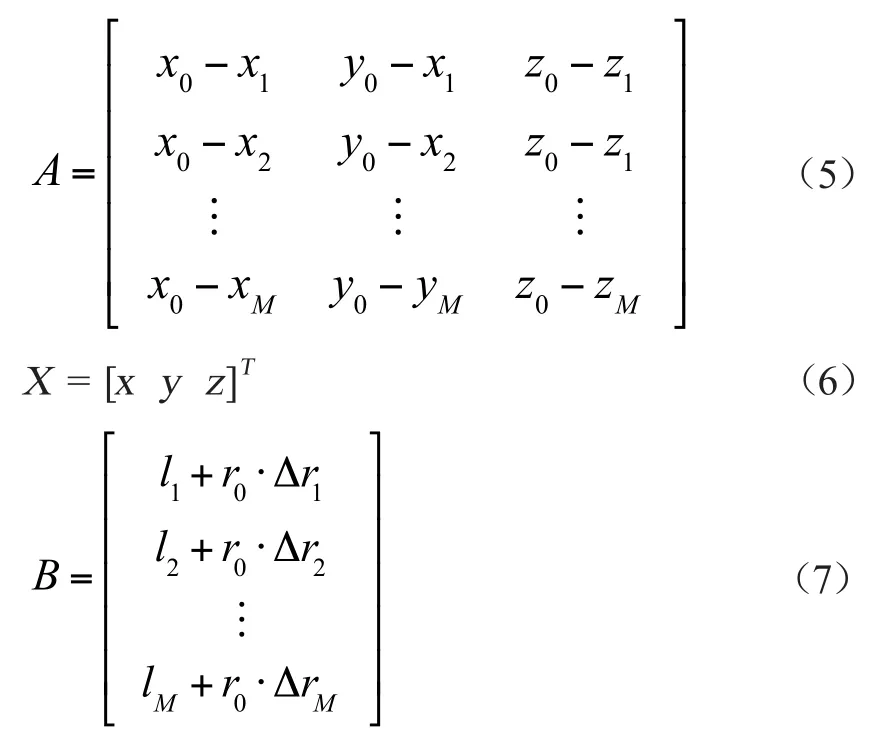
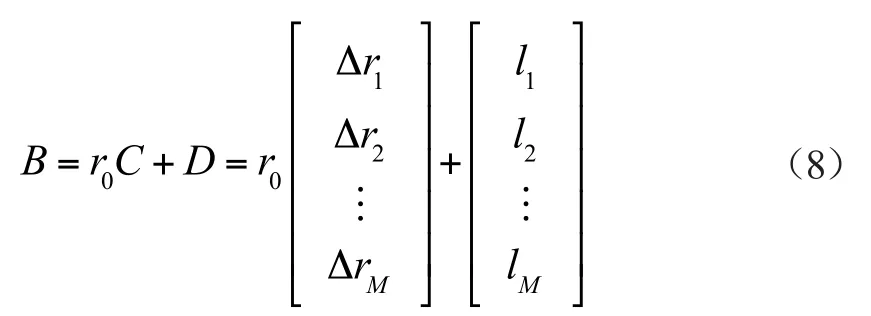
为方便求解,可以进一步把矩阵B分解为矩阵C和D
当M=3时,A为方阵,根据克莱姆法则可解得

式中,ai为AX=C的解;bi为AX=D的解;i=1,2,3。将式(9)带入式(2)得到

对式(10)求解可得

根据一元二次方程公式分析r0的求解情况:
(1)当B2-AC≥0时,方程有解,可以实现定位;
(2)当B2-AC=0时,方程仅有唯一解,即只存在一个交汇点,不会出现定位模糊;
(3)当B2-AC>0时,方程有两个解,即存在两个交汇点,会出现模糊定位;
(4)当B2-AC<0时,方程无解,即不存在交汇点,无法定位。
当式(10)有两个解,即存在定位模糊时,若两个解的乘积小于零,则取正数解,可消除定位模糊;若两个解的乘积大于零,即存在两个正数解,需要其他辅助数据才能消除定位模糊,一般可以借助测向数据,借助地理坐标计算两个定位点相对测向站的方位角,与实际测量目标辐射源的方位角进行比较,即可消除定位模糊点,得到正确的r0值。
2 定位误差分析
为分析不同参数对定位误差的影响,引入几何稀释度(Geometric Dilution of Precision, GDOP)的概念,它可以作为衡量无源定位精度的重要指标,清晰的描述定位误差的空间几何分布,GDOP值越小,表示定位精度越高。其表达式为

式中,PdE为定位误差协方差矩阵,可通过误差方程求得[7-8]。
对式(1)中Δri=ri-r0取全微分,可得

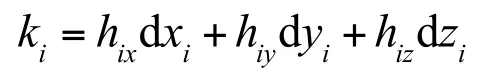
将式(14)写成矩阵形式
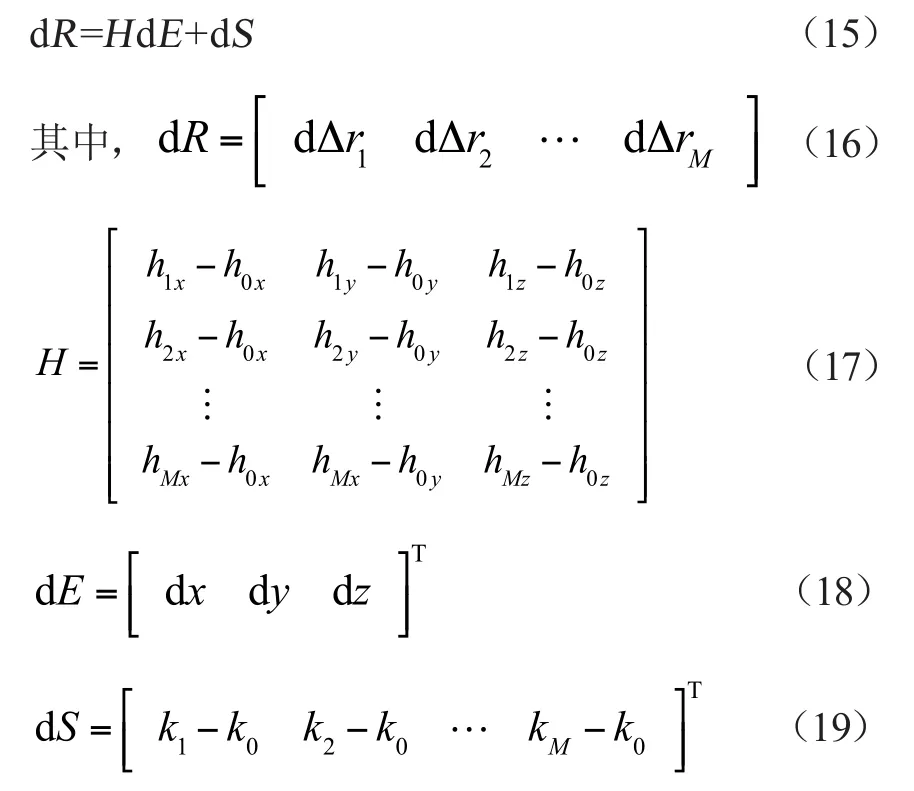
由式(15)可得
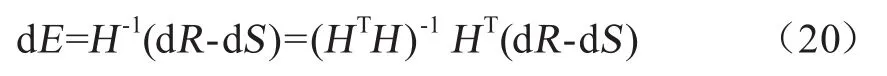
由式(20)可知,TDOA的定位误差主要由站址误差和距离误差决定,而距离误差等于光速与到达时间差的乘积,光速是恒定不变的,所以距离误差等同于到达时间误差。因为到达各辅助监测站的测量时差含有相同的误差因素,所以距离测量误差相关。设距离测量误差零均值,在每次测量到达时间差时,站址误差保持不变,并且导致站址误差的因素之间和站址误差之间互不相关,则定位误差的协方差为[9]

式中

假设站址误差各方向的标准差相同,可得到

由式(24)可知,影响定位精度的主要因素是到达时差测量误差和站址误差,目标辐射源与各监测站的位置关系与定位精度有关,到达时差测量误差和站址误差取决于设备精度,可视为TDOA定位系统的固有误差,所以我们主要分析不同的位置关系对受控区域定位精度的影响,选择合适的监测站部署位置。
3 实验仿真
在三维空间中定位目标辐射源的位置,至少需要三个距离差,由两站确定一个双曲面,因此至少需要四个监测站。为了更贴近实际情况,本文只选取四个监测站进行TDOA定位实验,假设测时差误差στ=5 ns,站址误差σs=0.005 km,目标辐射源高度z=10 km不变,四个红色圆圈表示监测站所在位置,仿真区域为x、y坐标轴-200~200 km构成的正方形范围内。
3.1 正方形布站
监测站坐标为S0(-10, 10, 0.3) km,S1(10, -10, 0.2)km,S2(-10, -10, 0.3) km,S3(10, 10, 0.2) km。GDOP分布如图3所示。
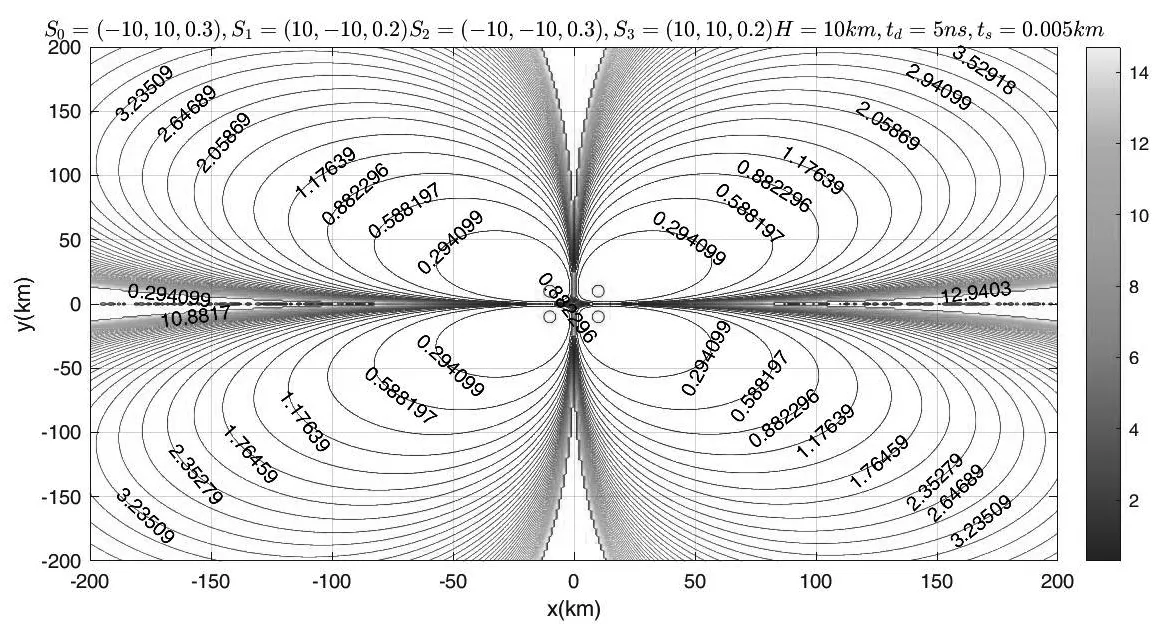
图3 正方形布站GDOP分布
监测站坐标为S0(-150, 150, 0.3) km,S1(150, -150,0.2) km,S2(-150, -150, 0.3) km,S3(150, 150, 0.2)km。GDOP分布如图4所示。

图4 正方形布站GDOP分布
3.2 菱形布站
监测站坐标为S0(-20, 0, 0.3) km,S1(0, 10, 0.2)km,S2(20, 0, 0.3) km,S3(0, -10, 0.2) km。GDOP分布如图5所示。

图5 菱形布站GDOP分布
3.3 平行四边形布站
监测站坐标为S0(0, 10, 0.3) km,S1(20, 10, 0.2)km,S2(-10, -10, 0.3) km,S3(10, -10, 0.2) km。GDOP分布如图6所示。
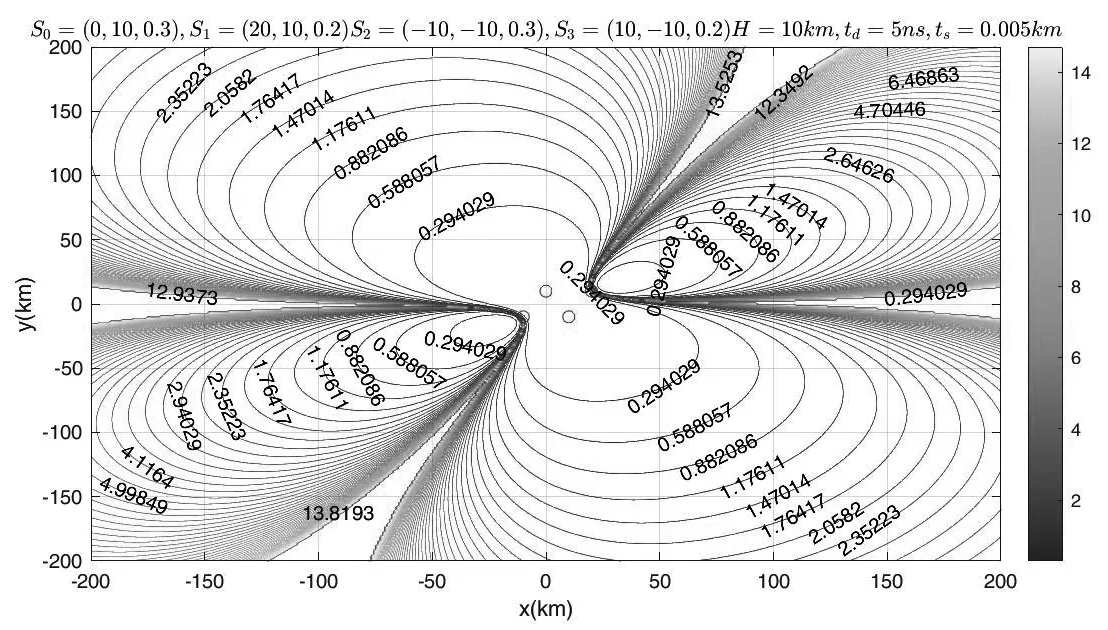
图6 平行四边形布站GDOP分布
3.4 三角形布站
监测站坐标为S0(-30, 30, 0.3) km,S1(0, 0, 0.2)km,S2(0, 30, 0.3) km, S3(30, 30, 0.2) km。GDOP分布如图7所示。
3.5 星形布站
监测站坐标为S0(-30, 30, 0.3) km,S1(0, 0, 0.2)km,S2(0, -30, 0.3) km,S3(30, 30, 0.2) km。GDOP分布如图8所示。
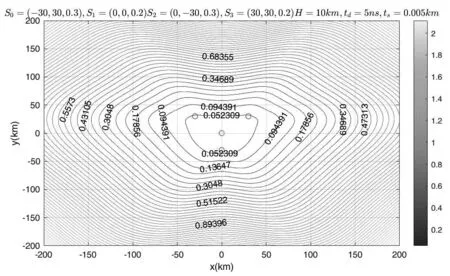
图8 星形布站GDOP分布
监测站坐标为S0(-150, 150, 0.3) km,S1(0, 0, 0.2)km,S2(0, -150, 0.3) km,S3(150, 150, 0.2) km。GDOP分布如图9所示。

图9 星形布站GDOP分布
3.6 结果分析
以上实验是在目标辐射源高度、测时差误差和站址误差不变的基础上完成的,从仿真结果可以看出,菱形、平行四边形和三角形布站的GDOP值分布在某些方向定位精度较高,但其他方向定位精度偏低;正方形和星形布站的GDOP值分布相对比较均匀,站间距增大后,定位精度明显提高;正方形布站的GDOP分布存在定位精度很差的方向,可以视为定位盲区;星形布站形式得到的GDOP值分布最均匀,且定位精度更高。
通过以上结果分析,可以得出以下结论:在目标辐射源高度、测试差误差和站址误差不变的前提下,星形布站形式定位精度高,受控区域大且GDOP值分布均匀,是相对理想的布站形式。在今后的无线电安全保障类工作中,对重点区域的无线电安全管控可以使用星形布站的形式,适当拉大站间距,使管控区域得到最优的定位精度。
4 结束语
本文通过研究时差定位原理,分析了影响定位误差的主要因素,并在固定测时差误差、站址误差和目标辐射源高度的前提下,分析了监测站布局对定位精度的影响,并得出结论,为今后无线电安全保障工作提供了布站形式的参考建议。

