转体球铰支座受力分析研究
白文阳





摘 要:转体铰支座作为转体桥梁的关键部位,其稳定工作影响着整个桥梁的稳定性。因此,研究转体铰支座的受力状态,通过有限元软件模拟球铰支座的变形及受力特性十分必要。本研究运用弹性力学、接触力学和有限元的相关知识,分析研究转体桥梁球铰支座的稳定性,模拟球铰支座的受力状态,可为同类型的转体桥梁的设计和施工提供借鉴。
关键词:转体桥;球铰支座;有限元分析;计算模拟;球铰应力
中图分类号:U448 文献标志码:A 文章编号:1003-5168(2022)2-0035-04
DOI:10.19968/j.cnki.hnkj.1003-5168.2022.02.008
Analysis on Bearing Force of Swivel Spherical Hinge Support
BAI Wenyang
(Beijing Xinqiao Technology Development Co., Ltd., Beijing 100000,China)
Abstract:The swivel hinge support is the key part of the swivel bridge, and its stable work affects the stability of the entire bridge. Therefore, it is necessary to study the force state of the swivel hinge support and simulate the deformation and force characteristics of the ball hinge support through the finite element software.This study uses the relevant knowledge of elasticity, contact mechanics, and finite element to analyze and study the stability of the spherical hinge bearing of the swivel bridge, and simulates the stress state of the spherical hinge bearing. The design and construction of the same type of swivel bridge provide reference and convenience.
Keywords: swivel bridge; spherical hinge bearing; finite element analysis; calculation simulation; spherical hinge stress
0 引言
桥梁作为跨越障碍物的主要建筑物,是公路和铁路建设中不可或缺的重要组成部分。由于许多桥梁所处环境比较特殊,传统的施工方法由于不具备施工条件无法实现桥梁的建造。转体桥梁作为交通技术行业发展的新产物,可以较好地解决上述问题。但是,转体桥梁支座的理论体系还不够完善,对转体桥梁支座的研究还处于探究发展阶段[1-2]。目前,转体桥梁支座技术的不成熟还体现在以下几个方面。
第一,国内现在对转体桥梁支座的设计、施工和研究是以多年来积攒的工程经验为基础的,缺乏一套完善的理论体系和明确的计算规范[3]。
第二,现有的理论体系是通过经验公式简化后得到的,现行《公路桥涵施工技术规范》(JTG/T F 50—2011)[4]将转体球铰的接触面简化为平面,规范中的一些计算公式以及相关系数的取值都是以早期拱桥的经验背景来规定的,用于其他桥型时可能会产生较大的误差,无法对转体球铰的细部结构进行分析,只能对球铰宏观的受力状态有所了解[5]。
本研究通过有限元软件ANSYS建立轉体球铰的局部模型,对球铰的局部进行分析计算,结合国内外的相关资料,得到一些有用的结论,对该类桥的施工起到一定的参考作用,也为之后相似桥梁的施工和设计提供参考。
1 球铰受力理论分析
1.1 理论分析
1.1.1 半平面体受法向集中力。将球铰的受力状态近似为弹性力学中的半平面体受法向集中力的问题,同时考虑半平面体在边界上存在集中力作用时,径向应力与径向角余弦值成正比,而具体到本研究中球铰的受力状态,认为球铰接触面上的正应力与径向角余弦值成正比[6],此时的竖向应力计算公式为[7-8]:
[σ=3Fcosθ2πR21-(R2-R21)32/R3] (1)
式(1)中:F为法向集中力;R为球铰半径;R1为球铰支撑半径;θ为径向角度。
1.1.2 简化方法。规范中采用的简化方法是将转体球铰的上下接触面近似为平面来处理,此时就简化为了平面接触应力问题,公式大大简化,此时的竖向应力计算公式为[4]:
[σ=FπR21] (2)
式(2)中:F为法向集中力;R1为球铰支撑半径。
1.2 弹性力学解析解与简化方法对比
在球铰支座的工程设计中,球铰圆心角取值的大小是球铰设计的关键环节。如果圆心角太小,则转体球铰的接触面就近似成为平面,此时球铰的摩擦系数会增大,启动力矩和摩擦力矩都会随之增大,这将会为桥梁的转体增加困难。若圆心角太大,则转体球铰的球铰半径也会随之增大,相对应的承台尺寸随之增大,造成不必要的资源浪费。下面选取几种不同半径、不同矢高的球铰支座,通过计算得到解析解与近似解,对比结果见表1,通过对比得到一些有用的结论。
由表1中的大量数据分析可以得到,转体球铰的半径一定时,其接触面的应力σ随着圆心角α的增大而减小。当圆心角一定时,转体球铰的接触面应力σ随着支撑半径R1的增大而减小。由于圆心角越小,转体球铰的接触面就越接近于平面,因此从表1中数据可以看出,解析解与近似解之间的误差随着圆心角α的增大而增大。通过表1的分析可以看到,弹性力学解析解与规范中简化公式的近似解误差范围为1.9%~4.5%,该误差范围在施工精度的可允许范围内。
转体球铰接触面内的竖向应力值在球面上各个位置的大小不一样,它取决于计算位置径向角的余弦值。而简化后的近似解不能体现这一特性,因此本研究认为弹性力学的解析解能够更加准确地反映出球铰的真实受力状态。转体球铰圆心角的大小决定了球铰的竖向应力值,球铰的最大应力值出现在接触面的外边缘。由于解析解的求解过程过于烦琐,实际工程设计中,在保证一定圆心角的情况下,可以将球铰接触面近似成平面进行设计,通过控制边缘竖向应力对球铰进行设计[9-12]。
2 球铰有限元数值分析
2.1 有限元模型的建立
笔者主要研究的是转体球铰模型的变形情况以及主压应力的分布情况,选择大型有限元通用软件ANSYS较为合适。因为球铰支座模型曲面较多,形状结构复杂多变,所以在选择单元的时候要考虑节点的数量,保证计算的精度。选择采用Structure Solid186单元,转体支座的整体模型如图1所示。磨盖为一个半径6.8 m的圆柱体,圆柱体的下表面是一个凸球面,球面半径为8 m;磨盖上表面与上转盘及上承台连接;磨心与下承台是一个整体,下承台为长44 m、宽29 m、高5 m的长方体,下承台的中心为一个与磨盖凸球面相对应的凹球面[13-16]。
2.2 球铰支座均布荷载下的受力
假设转体桥上部结构的重心与球铰支座的中心线重合,则转体结构的总重量全部都作用在球铰身上。上部结构的自重通过面均布荷载施加到上承台的顶面。同时,对下承台的下表面所有节点建立节点集合,对其施加X、Y、Z三个方向的平动及转动自由度的约束。通过ANSYS有限元分析计算,结果如图2所示。
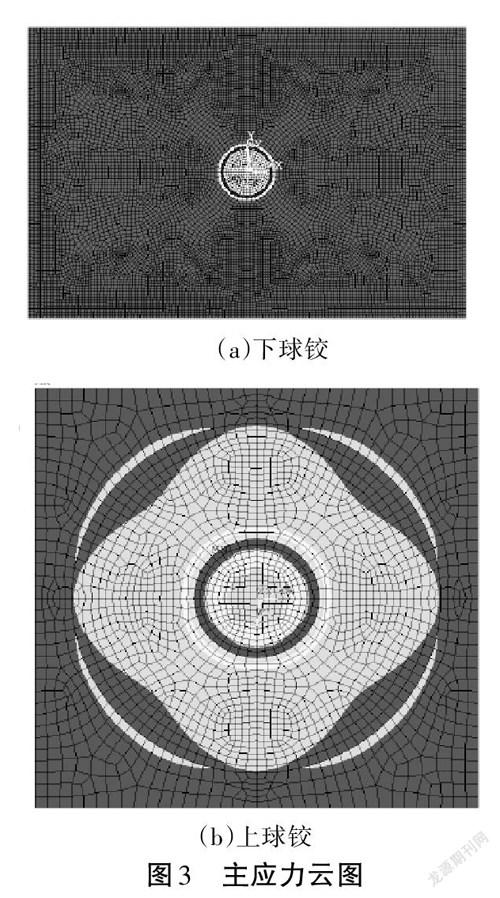
如图3所示,主压应力的最大值发生在球铰接触面的外边缘,接触面内的压应力沿接触面圆周方向分布均匀且在径向方向上呈梯度分布,呈现出中间小边缘大的变化趋势。上球铰接触面的应力分布规律与下承台磨心的应力分布一致,依然呈现出中间小边缘大的趋势。
3 转体球铰设计及支座承载力影响因素
3.1 矢高对支座承载力的影响
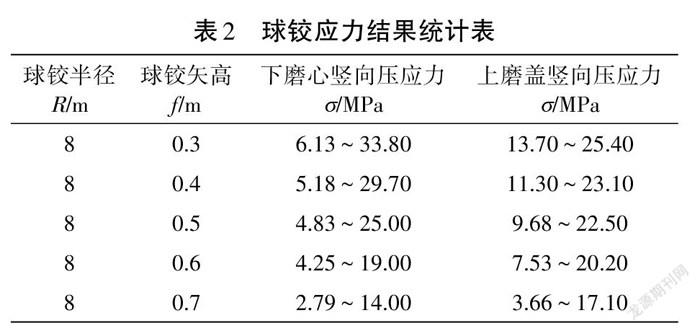
相同半径的球铰支座,矢高的改变能够直接影响球铰接触面的尺寸。在相同的受力状态下,通过ANSYS分析计算得到了相同半径下不同矢高的球铰支座的应力值,如表2所示。
在相同的球铰半径和相同的受力状态下,球铰的矢高越大,球铰间的应力越小。因此,可以在球铰半径保持不变的情况下,通过增加球铰支座的矢高来提高球铰支座的承载力。
3.2 球铰半径对支座承载力的影响
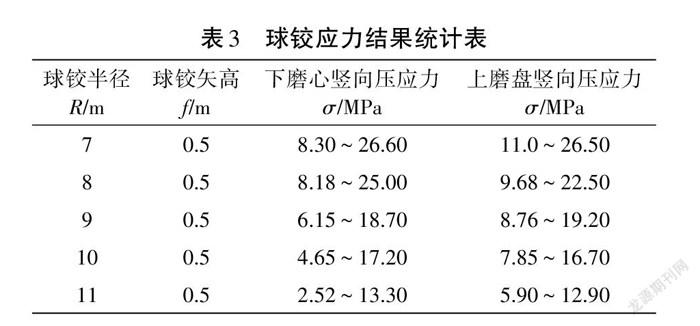
球铰的矢高保持不变,通过改变球铰的半径也可以影响球铰接触面的尺寸。在相同的受力状态下,通过ANSYS分析计算可以得到相同矢高下不同半径的球铰支座的应力值,如表3所示。
在相同的球铰矢高和相同的受力状态下,球铰的半径越大,球铰间的应力越小。因此,可以在球铰矢高保持不变的情况下,通过增加球铰支座的半径来提高球铰支座的承载力。
3.3 球铰半径与矢高同步变化对支座承载力的影响
通过分析得到矢径比相同但半径与矢高不同的各个球铰支座的应力值,如表4所示。
在相同的矢径比和相同的受力状态下,球铰的半径越大,球铰间的应力越小。
由以上结论可以看出,无论是改变球铰的半径还是球铰的矢高,它们都始终遵循一个规律:球铰接触面的面积越大,球铰的竖向应力就越小。但是随着球铰接触面面积的增大,球铰间的摩擦力也会随之增大,这样就会使得球铰的转动非常困难,可能需要一个很大的牵引转动力矩才能使球铰发生转动,这对转体桥的转体成功又造成了較大的阻碍。所以球铰尺寸的大小需要综合考虑球铰间的应力状态和接触面的摩擦力等多个因素。在牵引力矩受限的情况下,需要通过其他方法来提高球铰的承载能力,保证球铰的尺寸不会太大。
3.4 混凝土强度对支座承载力的影响
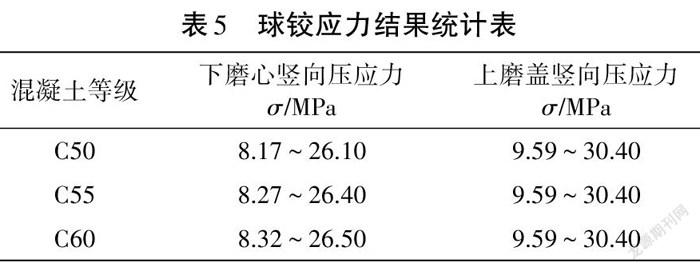
球铰的矢高与半径保持不变,通过改变球铰的混凝土强度等级也可以影响球铰支座的承载力。在相同的受力状态下,通过ANSYS分析计算可以得到,相同矢高相同半径下不同强度等级混凝土的球铰支座的应力值,如表5所示。
球铰的竖向应力值与混凝土强度的关系不大,球铰的受力状态基本保持不变。而C60的混凝土轴心抗压强度设计值要比C50混凝土的大,这样就能使球铰支座有一定的安全储备,承载能力得到了有效的提高。
4 结语
以弹性力学半平面体边界受集中力理论推导出球铰的接触应力求解公式,通过与规范中简化公式的对比发现,误差在施工可接受范围之内。因此,根据规范公式和基于弹性力学半平面体边界受集中力理论推导的公式估算的球铰接触应力是可行的。
通过ANSYS有限元的分析计算表明,中心受载的球铰磨心和磨盖的接触应力沿圆周方向分布均匀,沿径向呈现中间小、边缘大的分布规律。以转体球铰接触面应力为目标,通过有限元软件模拟不同尺寸参数的球铰,计算得到了不同球铰设计参数下接触应力值,给出了半径、矢高、矢径比以及混凝土强度与球铰接触应力的关系,提出了提高球铰承载力的合理建议,为以后转体桥梁的施工提供借鉴。
参考文献:
[1] 兰印龙.水平转体球铰力学分析与应用研究[D].石家庄:石家庄铁道大学,2018.
[2] 张新冈.平转法桥梁施工球铰分析及控制研究[D].北京:中国铁道科学研究院,2017.
[3] 张聪聪.转体桥球铰稳定与施工模拟分析[D].武汉:武汉理工大学,2016.
[4] 中华人民共和国交通运输部.公路桥梁施工技术规范:JTG/TF 50—2011[S].北京:交通运输部办公厅,2011.
[5] 王坤.T型悬臂梁平转施工关键技术的研究[D].天津:天津大学,2012.
[6] 左敏,江克斌.转体桥平转球铰转体过程应力计算方法研究[J].铁道标准设计,2015(12):40-43.
[7] 车晓军,周庆华,关林坤.转体施工桥梁大吨位球铰径向应力计算方法优化研究[J].武汉理工大学学报:交通科学与工程版,2014(2):356-358.
[8] 徐芝纶.弹性力学简明教程[M].北京:高等教育出版社,2013.
[9] 傅贤超,王正仪,王兴猛.轻型桥梁转动体系的研究分析[J].铁道建筑,2012(1):23-26.
[10] 马朝旭.连续梁平转施工转体球铰应力分析计算[J].兰州工业学院学报,2015(6):68-71.
[11] 朱永进.大跨度连续梁转体施工球铰局部应力分析[J].城市建设理论研究,2015(14):195-197.
[12] 李毓.新型大噸位桥梁转体支座受力性能计算与试验研究[D].天津:天津大学,2018.
[13] 李庆龄.ANSYS中网格划分方法研究[J].上海电机学院学报,2006(5):32-34.
[14]XIA Y D.Fabrication and Installation Control Technology of Swivel Continuous Beam Turntable for Extra Large Bridge across Dazheng Railway[J].Value Engineering,2017(33):136-139.
[15]QUAN A.Application of Weighing Technology in Construction of Continuous Beamand Swivel of Sui River Railway[J].Architectural Knowledge,2017(17):185-188.
[16]JOHNSON K L.接触力学[M].北京:高等教育出版社,1992.

