黏接界面各本构模型之间形状参数的关系研究
周亮 李晓雷 陈文义

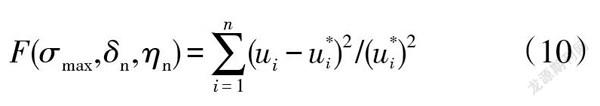

文章编号:1007-2373(2022)01-0035-07
摘要 指数型、多项式、三线型及双线性内聚力模型广泛用于表征黏接结构的界面性能,建立不同模型形状参数间的关系,可以为界面问题研究中参数的选取提供参考。首先,保持黏接界面的临界应力和断裂能相等,推导四4种模型形状参数之间的关系,任意2种模型的形状参数可相互表示。其次,基于改进的遗传算法反演识别率相关的铝合金黏接界面4种模型的形状参数,以指数型模型为基准,多项式、三线型及双线性模型形状参数反演识别与预测值的相对误差分别为1.76%、1.54%、3.13%。最后,根据各模型形状参数之间的关系给定4种模型界面参数,对比分析有限元仿真结果,4种模型表征的界面性能相同,验证了推导结果的准确性。
关 键 词 内聚力模型;形状参数;黏接界面;改进的遗传算法;参数反演识别
中图分类号 TG491; O346.5 文献标志码 A
Study on the relationship between shape parameters
of the bonding interface constitutive models
ZHOU Liang1, LI Xiaolei1, CHEN Wenyi2
(1. School of Mechanical Engineering,Hebei University of Technology, Tianjin 300401, China; 2. School of Chemical Engin-eering, Hebei University of Technology, Tianjin 300130, China)
Abstract Exponential, polynomial, trilinear and bilinear cohesive models are widely used to characterize the interfacial properties of bonded structures. Establishing the relationship between shape parameters of different cohesion models can provide reference for the selection of shape parameters in interface problem research. Firstly, when the critical stress and fracture energy of each model are kept equal, the relationship between the shape parameters of four models is derived. The shape parameters of any two models can be represented mutually. Based on the improved genetic algorithm, the shape parameters of rate-related bonding interface were identified. Secondly, based on the exponential model, the inversion and prediction value of polymorphism, three-line and bilinear model shape parameters were carried out. The relative errors of the values are 1.76%, 1.54% and 3.13%. Finally, according to the relationship between the shape parameters of each model, four model interface parameters are given. The simulation results show that the interface performance of the four models is the same, which verifies the accuracy of derivation results.
Key words cohesive model; shape parameter; bonding interface; improved genetic algorithm; parameter inversion recognition
0 引言
黏接結构广泛应用于机械制造[1]、航空航天[2]及柔性电子[3]等领域,黏接结构的失效往往发生在黏接界面[4],研究黏接界面的力学性能至关重要。Barenblatt[5]和Dugdale[6]最早提出了内聚力模型的概念,用于模拟和预测界面的开裂过程。随后,针对不同的材料,发展出各种形式的内聚力模型,其主要差别在于张力位移关系曲线形状的不同。Needleman等[7]将模型张力位移关系曲线简化为连续变化的抛物线,采用界面势函数的方法提出了多项式及指数型的非线性内聚力模型。Tvergaard和Hutchinson[8]计算弹塑性固体裂纹的扩展阻力时,基于经典的断裂力学将界面本构关系近似为梯形,建立了形状较为简单的三线型内聚力模型。Camacho等[9]研究脆性断裂问题时,将张力位移法则简化为三角形,基于连续损伤力学提出了单一形状的双线性内聚力模型。4种形状的内聚力模型广泛用于研究不同领域的界面问题。周清春等[10]基于指数型模型模拟了火箭推进剂绝热界面的开裂过程。张鹏等[11]采用多项式模型构造新型的奇异单元研究了双材料界面裂纹扩展问题。薛国宏等[12]针对柔性电子的金属薄膜界面,采用了本构方程为分段函数的三线型模型研究了延展性断裂过程。林德佳等[13]基于双线性模型分析了夹层玻璃界面在冲击载荷下沿界面端分层扩展过程。针对具有时间相关特性的黏接界面,Wang等[14]在Needleman模型的基础上提出了考虑黏弹效应的率相关内聚力模型。针对损伤问题,刘海涛等[15]融合了指数型及多项式模型的特点,提出了基于损伤的内聚力模型研究了沥青混凝土界面的开裂机理。
Blackman等[16]研究纤维复合材料双悬臂梁黏接界面的断裂问题时,仅考虑了断裂能和临界应力对界面性能的影响,忽略了形状参数的作用效果。近期的研究[17]表明,内聚力模型的形状参数对于表征黏接结构的力学状态至关重要。张军等[18]分析了不同形状内聚力模型和黏接结构断裂之间的关系,研究表明形状参数是确定拉伸和剪切断裂的重要参数。Li等[19]研究了金属陶瓷结合界面的裂纹扩展问题,模型的形状参数决定了裂纹扩展阻力的大小。Campilho等[20]分析了各模型参数对搭接接头模拟结果的影响,形状参数和临界应力的变化能够显著影响界面的黏接强度。Fernández-Cañadas等[21]基于指数型和三线型模型研究了搭接接头的开裂规律,界面失效时2种模型的载荷相同。Volokh[22]研究了双线性、多项式和指数型模型在刚体界面剥离测试中的作用效果,采用不同形状的内聚力模型实验测量得到的临界应力和断裂能均相等。钮然铭等[23]在保持断裂能相等的前提下,分别采用双线性及指数型模型研究了推进剂界面的分层扩展问题,构建了基于损伤的内聚力模型并与计算结果进行比较。模拟同一黏接界面时,基于能量的观点,界面失效时的断裂能相等,不同形状的内聚力模型都是描述界面单元的张力位移关系,各模型的形状参数之间应当存在一定的联系。
本文将采用4种典型的内聚力模型表征考虑黏弹效应的双悬臂梁黏接界面的力学性能。首先,保持黏接界面断裂能相等,推导不同内聚力模型形状参数之间的关系。其次,分别从参数反演识别及数值模拟正反两方面进行验证。一方面,基于改进的遗传算法反演识别铝合金黏接试件的各模型形状参数,分析其内在联系。此外,根据各模型形状参数之间的关系给定4种模型的界面参数,对比分析其仿真结果。
1 4种内聚力形状参数的关系推导
常用的内聚力模型有:指数型内聚力模型(E-CZM),多项式内聚力模型(P-CZM),三线型内聚力模型(T-CZM)及双线性内聚力模型(B-CZM)。
1.1 指数型内聚力模型
为了考虑黏弹效应对率相关的双悬臂梁黏接界面性能的影响,在时间无关的指数型内聚力模型基础上引入黏性系数[η],得到该模型张力位移关系表达式为
式中:[σmax]为法向临界应力值;[δEn0]为临界应力所对应的特征长度;[Δn]为相对位移;e为自然常数;t为单位时间。该模型断裂能为
1.2 多项式内聚力模型
简化后的多项式内聚力模型应力表达式为
式中:[δPnc]为该模型的临界张开位移。该模型断裂能为
1.3 双线性内聚力模型
双线性内聚力模型张力位移关系表达式为
式中:[δBn0]和[δBnc]分别为模型应力最大以及完全失效时的张开位移值。模型断裂能为
1.4 三线型内聚力模型
三线型内聚力模型张力位移关系表达式为
式中:[δTn0]、[δTn1]和[δTnc]分别为模型各应力状态所对应的张开位移。模型断裂能为
1.5 各模型形状参数关系推导
采用以上4种典型内聚力模型表征率相关的双悬臂梁黏接界面力学性能,假设断裂能相等,根据临界应力、断裂能以及形状参数三者间的关系,得到各模型形状参数之间关系:
4种内聚力模型中的任意2种模型的形状参数均可互相表示。其中:多项式、双线性模型的临界张开位移[δnc]与指数型模型的特征长度[δn0]可互相表示;三线型模型各应力状态对应的张开位移[δn0]、[δn1]和[δnc]与双线性及多项式的临界张开位移[δnc]可互相表示。
2 计算模型与分析方法
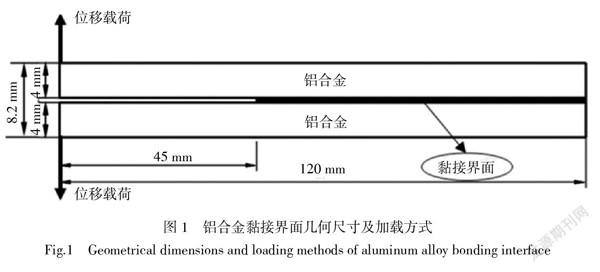
根据ASTM D344标准设计双悬臂梁黏接界面的几何模型,分析各模型形状参数之间关系。该模型由硅橡胶黏接剂和6061-T6铝合金板黏接而成,长为120 mm,宽为8 mm,厚度为8.2 mm。上下两铝合金板厚度均为4 mm,胶黏剂的厚度为0.2 mm,前端有45 mm的未黏接区域作为预制裂纹。选取模型左端面的上下两顶点施加位移载荷,几何尺寸及加载方式如图1所示。
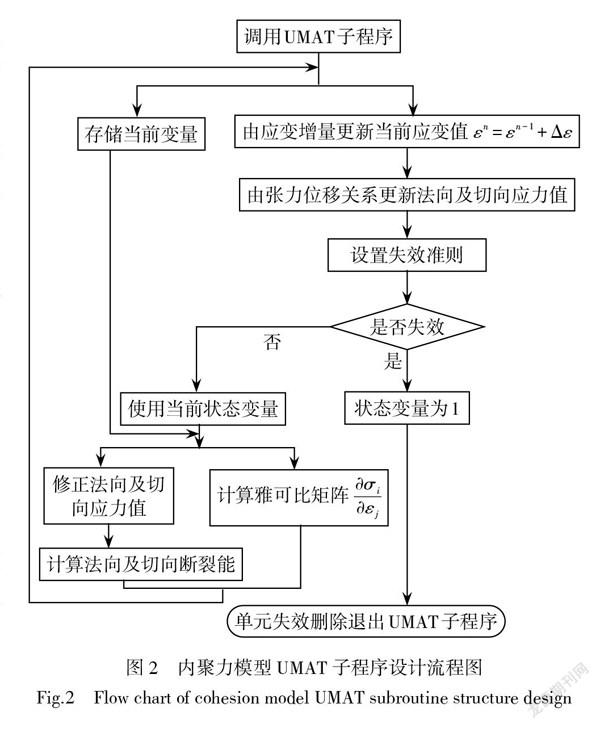
建立ABAQUS二维有限元模型,在界面处设置参考点,从而提取标记点的张开位移值。铝合金材料弹性模量E=70 GPa,泊松比[μ=0.33],屈服强度[σs]=270 MPa。铝合金采用四节点平面应力单元(CPS4R),胶黏剂采用四节点黏结单元(COH2D4)。黏接界面划分为一层有厚度的单元。采用4种不同形状的内聚力模型编译UMAT子程序表征界面单元的材料属性,通过判断法向或切向断裂能是否达到临界值来控制界面单元的失效删除,流程图如图2所示。子程序中用来表征黏接界面力学性能的模型参数即为待反演識别的参数。
3 各模型形状参数反演识别及其关系验证
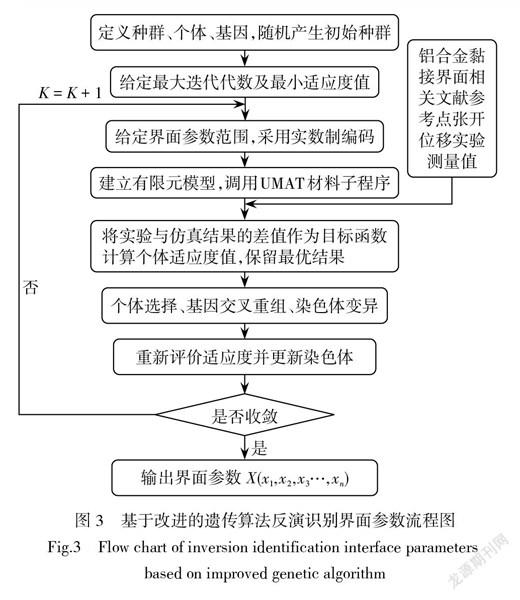
基于改进的遗传算法极小化目标函数反演识别铝合金黏接界面参数,分析各内聚力模型形状参数之间的关系。算法采用实数制编码,分区域划分搜索区间,种群大小设置为26,初始交叉概率为0.6,初始变异概率为0.08,最大迭代代数为50,动态调整交叉及变异概率。
利用文献[24]中界面参考点张开位移的实验测量值与数值模拟值构造目标函数,表达式为
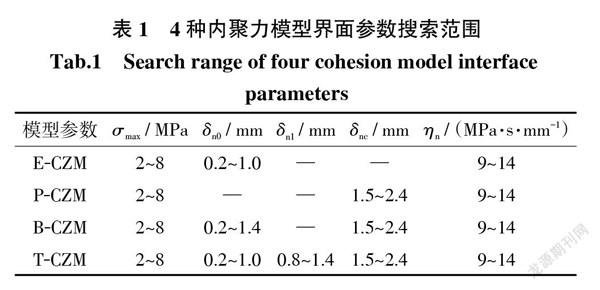
式中:[ui]为有限元模拟得到的参考点张开位移;[u*i]为实验测量的张开位移。整个反演分析过程通过Python编译的算法程序自动完成。按表1给定的参数范围,结合遗传算法和有限元迭代无限逼近最优解,具体流程如图3所示。
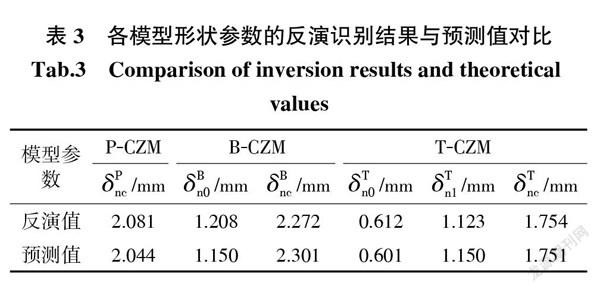
表2为各模型参数反演结果,取4者的均值作为界面参数,临界应力为4.91 MPa,断裂能为5.63[N∙m-1],黏性系数为12.12[MPa∙s∙m-1]。本文指数型模型的临界应力和张开位移为4.91 MPa和0.423 mm。文献[24]为4.83 MPa和0.431 mm,两者的相对误差仅为1.61%和1.88%。
以反演識别的指数型模型的形状参数为参考,根据各模型形状参数之间的关系得到另外3种模型的形状参数。多项式模型形状参数的反演识别与预测值的相对误差为1.76%。三线型模型形状参数[δBn0]及[δBnc]的反演识别与预测值的相对误差分别为4.9%和1.23%。将其求平均值可得到三线型模型形状参反演识别与预测值的相对误差为3.13%。线性模型模型形状参数为[δTn0]、[δTn1]及[δTnc],其反演识别与预测值的相对误差分别为1.79%、2.4%和0.17%。将其求平均值可得到三线型模型形状参反演识别与预测值的相对误差为1.54%。线性模型、反演识别与预测值之间的误差较小,验证了所推导关系的准确性。
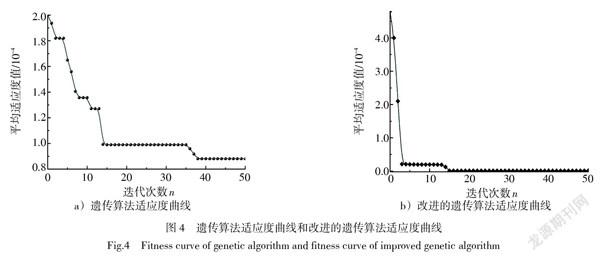
将改进的遗传算法与改进前进行对比,分析其优点。图4a)为遗传算法的迭代曲线图,适应度函数在开始时收敛速度较快,然后有梯度地逐渐趋于稳定。图4b)则采用了改进的遗传算法,适应度函数快速收敛到极小值后处于稳定状态,有效地缩短了模型调用时间。
4 有限元分析及各模型形状参数的关系验证
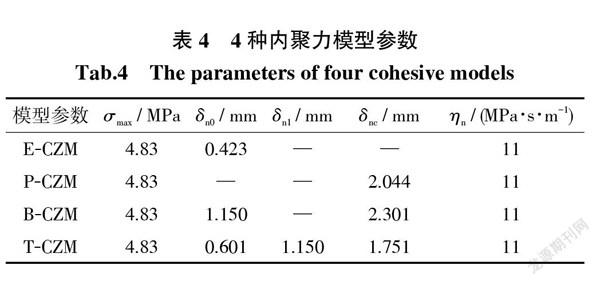
给定指数型模型参数,保持临界应力和黏性系数相同,根据各模型形状参数之间的关系给定另外3种模型参数,其设置如表4所示。基于给定的界面参数建立有限元模型,对4种模型的仿真结果进行分析,从数值模拟的角度验证各模型形状参数之间的关系。
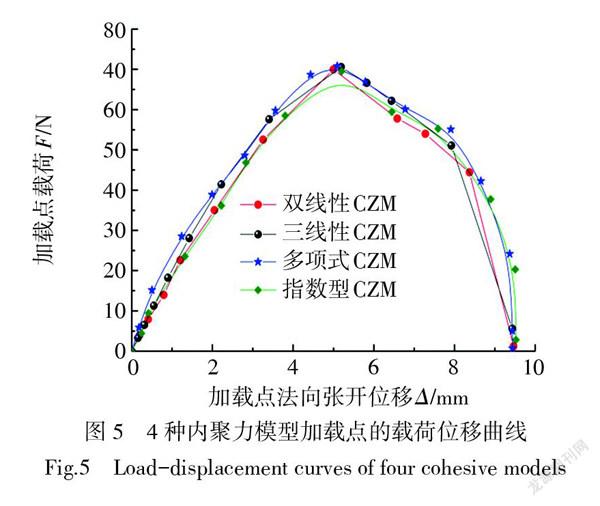
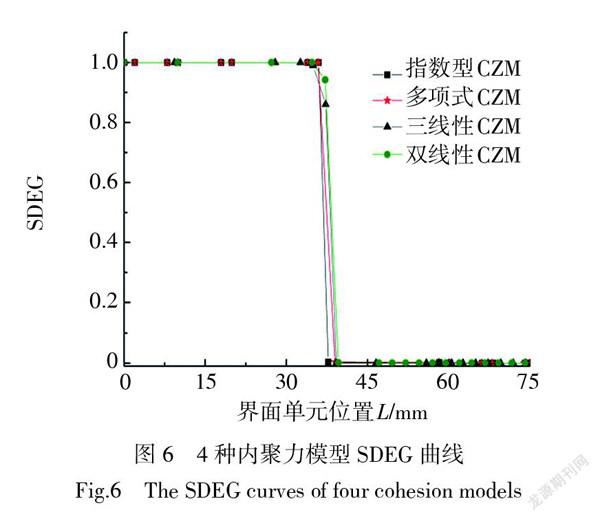
图5为4种模型加载点的载荷位移曲线,最大载荷值均为70.4 N,界面开始失效时的法向张开位移均为5 mm。曲线上升阶段,多项式和指数型模型重合度较好。下降阶段,三线型与多项式模型较为吻合。多项式、三线型及双线性模型数值模拟得到的载荷值与指数型的相对误差为2.46%、2.11%、1.12%。图6为各模型加载点的张开位移为6.2 mm时的界面单元删除状态曲线,当界面位置小于36 mm时,SDEG值均为1,界面单元失效删除,基于4种子程序计算得到的界面撕裂破坏程度相等。
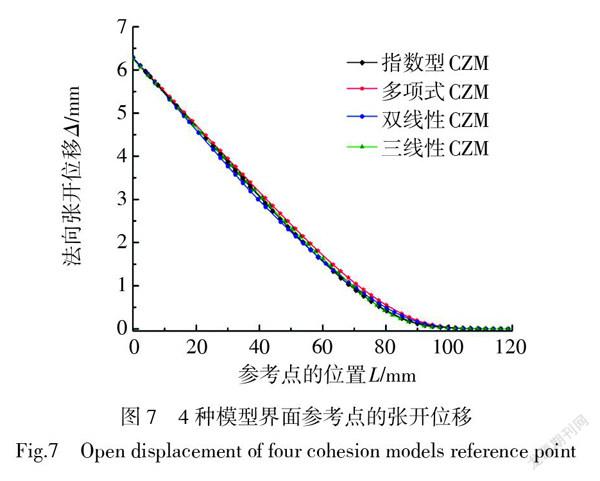
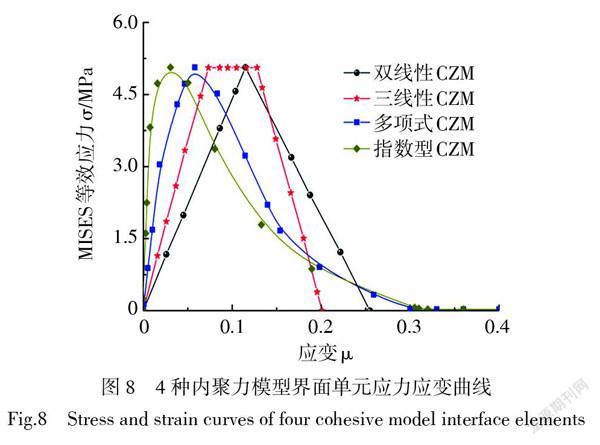
4种模型参考点的张开位移如图7所示,多项式、三线型及双线性模型各参考点的张开位移与指数型模型张开位移的相对误差分别为1.04%、1.82%、2.01%。图8为各模型界面单元的应力应变曲线,所围成的面积均为0.65,表明各模型的临界断裂能相等。
5 结论
1) 采用不同形状的内聚力模型表征黏接结构的界面性能,推导了4种模型形状参数之间的关系。任意2种模型的形状参数均可相互表示, 基于其中1种模型可得到另外3种模型的形状参数,为界面问题研究中模型参数的选取提供参考。
2) 基于改进的遗传算法反演识别了铝合金黏接试件各模型的形状参数。以指数型模型为标准,多项式、三线型及双线性模型形状参数反演识别与预测值的相对误差分别为1.76%、1.54%、3.13%,各模型形状参数之间符合所推导的关系。
3) 基于各模型形状参数之间的关系给定4种模型的界面参数,对比分析其仿真结果。4种模型加载点的载荷位移曲线以及SDEG曲线均趋于吻合,各参考点的张开位移值相等。结果表明4种模型表征的界面性能相同,验证了所推导结果的准确性。
参考文献:
[1] 胡平,韩啸,李伟东,等. 考虑汽车车身涂装工艺影响的非平衡胶接接头强度[J]. 机械工程学报,2012,48(20):96-105.
[2] 李雪换,底月兰,王海斗,等. 基于内聚力模型的热障涂层失效行为研究[J]. 材料导报,2019,33(9):1500-1504.
[3] 王晓玲,李豪,王国庆. 柔性基板的几何参数对柔性电子系统延展性的影响[J]. 工程科学学报,2015,37(S1):24-28.
[4] MAY M,HESEBECK O. Failure of adhesively bonded metallic T-joints subjected to quasi-static and crash loading[J]. Engineering Failure Analysis,2015,56:454-463.
[5] BARENBLATT G I. The mathematical theory of equilibrium cracks in brittle fracture[J]. Advances in Applied Mechanics,1962,7:55-129.
[6] DUGDALE D S. Yielding of steel sheets containing slits[J]. Journal of the Mechanics and Physics of Solids,1960,8(2):100-104.
[7] NEEDLEMAN A. An analysis of tensile decohesion along an interface[J]. Journal of the Mechanics and Physics of Solids,1990,38(3):289-324.
[8] TVERGAARD V,HUTCHINSON J W. The relation between crack growth resistance and fracture process parameters in elastic-plastic solids[J]. Journal of the Mechanics and Physics of Solids,1992,40(6):1377-1397.
[9] CAMACHO G T,ORTIZ M. Computational modelling of impact damage in brittle materials[J]. International Journal of Solids and Structures,1996,33(20/21/22):2899-2938.
[10] 周清春,鞠玉涛,周长省. 基于Hooke-Jeeves算法的挠性粘接件的高效内聚反演分析[J]. 工程力学,2015,32(4):1-7.
[11] 张鹏,胡小飞,姚伟岸. 内聚力模型裂纹问题分析的解析奇异单元[J]. 固体力学学报,2017,38(2):157-164.
[12] 薛国宏,陶伟明. 金属材料延性对其薄膜-柔性基底结构延展性的影响[J]. 力学季刊,2013,34(2):270-274.
[13] 林德佳,臧孟炎. 基于内聚力模型的夹层玻璃冲击破坏仿真分析[J]. 机械工程学报,2017,53(22):176-181.
[14] WANG J,KANG Y L,QIN Q H,et al. Identification of time-dependent interfacial mechanical properties of adhesive by hybrid/inverse method[J]. Computational Materials Science,2008,43(4):1160-1164.
[15] 刘海涛,严明星. 基于改进的内聚力模型模拟沥青混合料裂纹扩展[J]. 城市道桥与防洪,2015(8):222-226,24.
[16] BLACKMAN B R K,HADAVINIA H,KINLOCH A J,et al. The use of a cohesive zone model to study the fracture of fibre composites and adhesively-bonded joints[J]. International Journal of Fracture,2003,119(1):25-46.
[17] YAN Y B,SHANG F L. Cohesive zone modeling of interfacial delamination in PZT thin films[J]. International Journal of Solids and Structures,2009,46(13):2739-2749.
[18] 张军,贾宏. 内聚力模型的形状对胶接结构断裂过程的影响[J]. 力学学报,2016,48(5):1088-1095.
[19] LI H,CHANDRA N. Analysis of crack growth and crack-tip plasticity in ductile materials using cohesive zone models[J]. International Journal of Plasticity,2003,19(6):849-882.
[20] CAMPILHO R D S G,BANEA M D,NETO J A B P,et al. Modelling of single-lap joints using cohesive zone models:effect of the cohesive parameters on the output of the simulations[J]. The Journal of Adhesion,2012,88(4/5/6):513-533.
[21] FERNÁNDEZ-CAÑADAS L M,IVÁÑEZ I,SANCHEZ-SAEZ S. Influence of the cohesive law shape on the composite adhesively-bonded patch repair behaviour[J]. Composites Part B:Engineering,2016,91:414-421.
[22] VOLOKH K Y. Comparison between cohesive zone models[J]. Communications in Numerical Methods in Engineering,2004,20(11):845-856.
[23] 鈕然铭,陈雄,周长省,等. 基于损伤的HTPB推进剂/衬层界面内聚法则构建[J]. 固体火箭技术,2014,37(6):819-823.
[24] 王效贵,裴佳雄,翁晓红,等. 基于数字图像相关法的内聚力模型参数反演识别[J]. 浙江工业大学学报,2016,44(6):676-680.
收稿日期:2019-09-14
基金项目:国家自然科学基金(11572357,11672162)
第一作者:周亮(1995—),男,硕士研究生。 通信作者:李晓雷(1972—),男,副教授,lixiaolei_hebut@163.com。

