分布式存储系统中自适应纠删码的研究综述

陈欢华

（广州软件学院网络中心，广州 510990）

0 引言

为了应对爆炸性的数据增长，如今的存储系统通常在多个地理位置部署数千个商品存储节点或服务器，以提供大规模的存储服务。这些系统通常构建在常见的组件上，这些组件更容易发生故障。软件故障、机器重启、维护停机、电源故障也可能使数据随时不可用，因此这些系统应保证数据的可靠和持久存储。为了在发生故障时保持数据的可靠性和可用性，传统的分布式存储系统通常采用冗余技术，如三副本［1-2］。当数据量较小时，冗余方法直接有效；然而，在大型数据中心，复制带来的200%的存储开销是巨大的，无法接受。作为一种折衷方案，纠删码是一种存储高效的容错技术，可以提供相同或更高级别的可靠性，同时需要更少的数据冗余［2］。因此，纠删码变得越来越流行，并被包括Microsoft［3］和Facebook［4］在内的企业广泛采用。

为了响应不同的访问特性［5］和满足动态可靠性要求［6］，现代存储系统需要纠删码具备自适应功能。自适应纠删码，指的是编码参数和编解码方案随着各类要求的变化。我们认为自适应纠删码在以下场景中是至关重要的。

（1）适应倾斜和动态的工作负载。实际存储系统中的工作负载是非常倾斜和动态的。倾斜意味着一小部分热数据被频繁访问，而大部分冷数据很少被访问，而动态属性意味着数据热度是随时间变化的。为了兼顾高访问性能和高存储效率，实际的存储系统可以使用高冗余纠删码存储热数据以获得高性能，同时使用低冗余纠删码存储冷数据以获得低成本持久化。当数据热度变化时，执行自适应以更新编码参数或者更改编解码方案［7］。

（2）适应不同的可靠性。不同生命周期的数据需要不同程度的可靠性，因此存储系统需要动态调整编码参数以满足不同的可靠性需求。此外，磁盘可靠性会随着磁盘的老化而变化。为了在存储开销和容错之间提供有效的权衡，大型数据中心应该弹性调整编码参数［6］。

（3）生成宽条带。最近的工作探索了用于纠删码存储的宽条带，以抑制条带中奇偶校验块的比例，从而实现极大的存储节省［5］。为了有效地支持宽条带，存储系统可以为新写入的数据部署具有适度低冗余的窄条带，然后将老化的数据转换为具有极低冗余度的宽条带［8］。

本文将通过介绍一些典型和常用的自适应纠删码来展示当前自适应纠删码研究的现状，并从评价这些码的各项重要指标的角度比较和分析现有的自适应纠删码，指出当前存储系统自适应纠删码研究中尚未解决的难题以及未来可能的研究方向。

1 基本概念

为了便于理解，通常将一个服务器称为一个节点，下面对本文出现的相关概念给出如下说明。

a）数据块：编码的最小数据单元。通常，系统将用户的原始数据划分成k个数据块。

b）校验块：指原始数据块经过编码运算得到的冗余块，块的大小与数据块大小相同。

c）条带：指多个数据块与其对应的校验块所构成的块集合。

d）辅助节点：指参与数据修复的可用节点。辅助节点读取本地数据后通过网络传输给其他节点来参与数据重建。

e）机架：若干个服务器和存储设备的集合。数据服务器和同一机架中的存储设备之间的访问速度非常高，而机架间的访问速度则较慢。

2 存储系统中的纠删码

2.1 基础纠删码

2.1.1 RS（Reed-Solomon）码［9］

RS 码可用两个可配置的参数k和m构造，用RS(k,m)表示。RS(k,m)将k个数据块作为输入进行编码，生成m个奇偶校验块，使得任意k+m个数据和奇偶校验块中的k个足以重建原始的k个数据块。一起编码的k+m个数据和奇偶校验块共同形成一个条带。一个实际的存储系统包含多个独立编码的条带。它将k+m个块的每个条带分布在k+m个节点上，以容忍任何m个节点故障。图1 给出了(k,m)=（4,2）的RS示例。

图1 RS（4，2）示例图

RS 码的存储开销小，但其修复开销高。修复任何一个故障块，均需从其余k个可用节点中读取k个块，然后经过计算得到。它的通信开销是故障块大小的k倍。

2.1.2 HH（Hitchhiker）码［10］

图2 显示了HH（6,3）码的示例。在HH(k,m)码中，每个条带分为两个子条带（a={ai}和b={bi}）。每个条带中有k个数据块和m个奇偶校验块，每个块分别由a和b中的一个符号共同组成，因此每个子条带中有k个数据符号和m个奇偶符号。编码时，对同一子条带的数据进行RS(k,m)编码，得到RS 码的奇偶符号。然后，将子条带a中的k个数据符号分成m-1 个组，每个组中的数据符号经过按位异或得到组内的校验符号。然后，将各个组中的校验符号和子条带b经过RS编码得到的奇偶块进行按位异或，以此得到子条带b最终的校验符号。

图2 HH（6,3）示例图

当有一个数据块故障时，HH 码可以运行快速解码过程来恢复丢失的数据块。请注意，子带b中的一个奇偶校验符号仍保留为RS 奇偶校验符号。该符号仅足以恢复子条带b中丢失的一个数据符号。假设子条a中的丢失符号在对应于奇偶校验符号bk+i+1的组Gi中。在完整的子带b的帮助下，可以计算组Gi的XOR 和。这意味着可以只读取该组中的其他数据符号来恢复子条带a中丢失的符号。整个过程只需要读取k+k/(m-1)k个符号。当m＞2 时，有k+k/(m-1)=km/(m-1) ＜k，这意味着与普通解码过程相比，快速解码过程可以减少网络带宽和磁盘I/O 的使用。

2.1.3 LRC(Locally Repairable Codes)码[4]

LRC 可用3 个参数(k,l,g)构造，意味着有k个数据块，l个本地奇偶校验块和g个全局奇偶校验块。一起编码的k+l+g个数据/奇偶校验块的集合称为条带，大型存储系统通常包含多个独立编码的条带。

在LRC 中，LRC 将k个数据块分成l个大小相等的组。它根据每组k/l数据块计算XOR 和以形成l个本地奇偶校验块。它还从所有k个数据块中计算g个全局奇偶校验块，计算方法同RS码。设b是编码成本地奇偶校验块的数据块的数量，即b=k/l。我们将b个数据块及其对应的本地奇偶校验块的集合称为本地组。图3 给出了(k,l,g)=(6,2,2)的LRC示例。

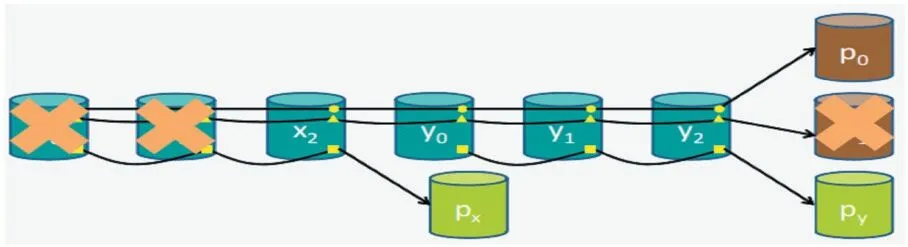
图3 LRC（6，2，2）示例图

在修复任何不可用的数据块时，LRC 检索同一本地组的其他可用块，而不是k个块，故LRC将通信开销降为故障块大小的b倍。

2.2 自适应纠删码

2.2.1 HACFS［7］

HACFS 使用来自同一码系列的两种不同纠删码。即，使用具有低恢复成本的快速码和具有低存储开销的紧凑码，如图4（a）所示。它利用在Hadoop 工作负载中观察到的数据访问偏差来决定数据块的初始编码。在初始编码之后，HACFS 系统通过使用两种新颖的操作在快速码和紧凑码之间转换数据块来动态适应工作负载的变化。将最初用快速码编码的块升级为紧凑码，使HACFS 系统能够减少存储开销。类似地，将数据块从紧凑码下编码为快速码，使HACFS 系统降低整体恢复成本。上码和下码操作非常有效，并且只在两个码之间转换时更新相关的奇偶校验块。

2.2.2 HeART［11］

HeART利用异构级别的可靠性来权衡长期的存储和恢复性能。HeART的基本思想是对高风险数据采用一种恢复速度快的码，在低风险时期采用另一种存储效率高的码，如图4（b）所示。

图4 HACFS和HeART方法的基本框架

2.2.3 Repair-Scale［12］

Repair-Scale 考虑了两组LRC 参数的变化，以响应工作负载的变化。具体来说，Repair-Scale考虑了两种LRC 结构：①快速LRC，它存储更多本地奇偶校验块以获得更高的修复性能（例如，用于热数据），以及②紧凑型LRC，它存储更少的本地奇偶校验块以获得更高的存储效率（例如，对于冷数据）。快速和紧凑的LRC都存储相同数量的数据块和全局奇偶校验块。执行缩放操作以在快速LRC 和紧凑LRC 之间切换，以平衡访问性能和存储效率。从快速LRC缩放到紧凑LRC 称为上编码，从紧凑LRC 缩放到快速LRC 称为下编码。因此，将上行编码成本和下行编码成本定义为分别为上行编码和下行编码传输的跨集群网络流量。

图5 描绘了(k,l,g,c)=(12,6,2,20) 的快速LRC 和(k,l,g,c)=(12,2,2,16)的紧凑LRC 的上编码和下编码。这两个码都部署在分层数据放置下（即，每个块都存储在不同的集群中，参数c指机架数）。上编码操作（从(12,6,2,20) 到(12,2,2,16)）将L1和L2跨集群发送到L0以计算新的本地奇偶校验块L'0，并将L4和L5跨集群发送到L3计算一个新的本地奇偶校验块L'1。因此，上编码成本为4。另外，下编码操作（从（12，2，2，16）到（12，6，2，20））将D2和D3发送到另一个集群以计算L1，并且将D4和D5发送到另一个集群以计算L2。然后它将L1和L2发送到持有L'0的集群以计算L0。L3、L4和L5也是如此。总共，下编码成本为12。

图5 快速LRC（12，6，2，20）和紧凑LRC（12，2，2，16）的上下编码示例

2.2.4 SRS［13］

SRS 码建立在块到节点映射的解耦之上，通过将RS 码的k个数据块存储在k'个节点中，其中k≤k'。ERS 首先计算k和k'的最小公倍数LCM，即l=lcm(k,k')，并将一个对象划分为l个数据块。然后将l个数据块排列成k个逻辑列，对每k个具有相同逻辑偏移量的数据块进行编码，计算出m个奇偶校验块。最后将l个数据块分布在k'个节点上，使得每个节点恰好存储l/k'个块，并将奇偶校验块分布在m个节点上。请注意，对于l/k个条带，奇偶校验块放在相同的m个节点上，而对于不同的条带组，则将奇偶校验块放在不同的节点上，以平衡奇偶校验更新的I/O 开销。由于数据块现在分布在k'个节点上，当对象从RS(k,m)转换到RS(k',m)时，SRS 码不需要数据块重定位，如图6所示。

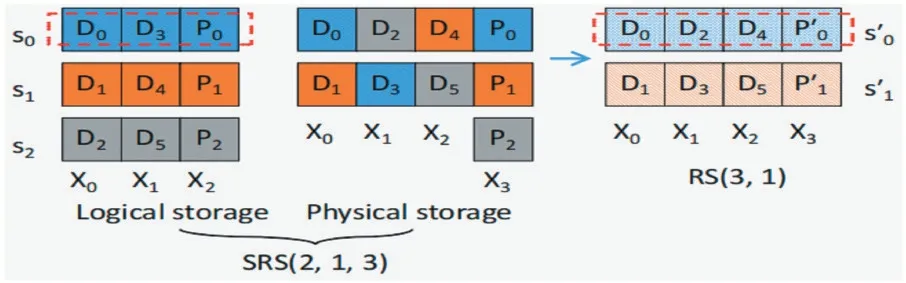
图6 SRS（2，1，3）示例图

2.2.5 ERS［14］

ERS 编码与SRS 编码在以下方面有所不同。首先，ERS 编码在逻辑上将l个数据块按行优先顺序分配到k个节点中，因此引入了大量重叠数据块用于冗余转换（如图7）。此外，ERS 编码使用新颖的编码矩阵对每k个数据块进行编码，并根据新颖的放置策略将l个数据块物理分布在k'个节点上，以增加重叠数据块的数量。因此，ERS 编码只需要少量的非重叠数据块，并且可以减少奇偶校验块更新的I/O。

图7 显示了按行优先顺序放置的ERS（2，1，3）示例。由于k=2 和k'=3，我们可以推导出l=lcm(2,3)=6。首先将l=6 个数据块顺序排列成k=2 逻辑行主要顺序的列。每k=2 个具有相同逻辑偏移量（即图中相同颜色）的数据块在逻辑存储中被编码为m=1个奇偶校验块。然后，l=6个数据块在物理存储中也以行优先顺序在k'=3个节点上物理拉伸。可以看到，RS（3,1）的数据块分布被保留了，因此在从RS（2,1）到RS（3,1）的转换过程中消除了数据块重定位。我们还可以证明P'0=P0+D2，并且P'1=P2+D3=P2+P1+D2。因此，只需要检索D2来更新冗余转换中的奇偶校验块。

图7 ERS（2，1，3）示例图

2.2.6 LRC-HH［15］

LRC-HH 自适应码选择两类码来应对访问倾斜的情况。其中快速码为LRC(k,m-1,m)码，紧凑码为HH(k,m)码。当快速码的编码数据转换为紧凑码的形式时，可以将LRC 中的两个条带（a和b）视为HH 代码中的条带的两个子条带（sa和sb），因此LRC 中的所有块都可以视为符号。所有数据符号都可以保留，a中的所有全局奇偶符号都可以保留为sa中的奇偶符号。在b中，第一个全局奇偶校验符号可以保留为sb中的第一个奇偶校验符号，但是sb中的其余奇偶校验符号是b中的全局奇偶校验符号与其对应的a中的数据符号组的异或和。为了计算和，不必读取a中的所有数据符号。相反，a中的原始局部奇偶校验符号正是应计算的部分和。因此，要计算sb中的奇偶校验符号，只需读取a中相应的局部奇偶校验符号，并将其与b中的原始全局奇偶校验符号进行异或。图8 显示了当k=6 和m=3时这种码切换过程的示例。

图8 从LRC（6,2,3）码到HH（6,3）码的转换

当HH(k,m)编码的数据转换为LRC（k,m-1,m）形式时，可以将HH 代码中的条带的两个子条带（sa和sb）视为LRC 的两个条带（a和b）。类似地，所有数据符号都可以作为数据块保留，sa中的所有奇偶校验符号可以作为a中的全局奇偶校验块保留。所有的本地奇偶校验块都只能通过数据块来计算，这部分计算是难以避免的。sb中的第一个奇偶校验符号可以保留为b中的第一个全局奇偶校验块。在这个阶段，b中的其余全局块可以在没有任何数据块的参与的情况下计算出来。要计算b中的全局符号，只需将a中的相应局部奇偶校验块（刚刚计算）与sb中的原始奇偶校验符号进行异或。图9 显示了当k=6 和m=3时此码切换过程的示例。

图9 从HH（6，3）码到LRC（6，2，3）码的转换

2.2.7 EC-Fusion［16］

为了应对动态的工作负载，需要在混合纠删码之间进行码转换，这是EC-Fusion 的核心模块。在构造RS(k,m)的基础上，我们可以将奇偶校验矩阵分解为几个大小为m×m的子矩阵。然后校验块生成方程可以重写为

由于RS 码中奇偶校验矩阵的任何m×m子矩阵都是可逆的，所以每个中间具有以下性质，

然后可以很容易地建立中间奇偶校验和MSR 奇偶校验之间的转换。其中“Trans1”和“Trans2”可以推导出如下表达：

因此，中间校验块可以作为实现RS 和MSR之间高效转换的桥梁。如图10（a）所示，对于从MSR 码到RS 码的转换，可以将原始奇偶校验的k/m组转换为中间奇偶校验，然后将它们合并为最终的RS 奇偶校验。

从RS 到MSR 的转换可以看作是一个逆过程，其中一组原始RS 被划分为最终的k/m组MSR。细节如图10（b）所示，其中(k/m)-1 组数据乘以它们对应的子矩阵。这样就可以通过所有现有的校验位得到最后一组的中间校验位，然后将所有中间校验位转化为最终的MSR码。

图10 MSR码与RS码之间的转换

3 自适应纠删码的比较与分析

3.1 评价指标

我们使用码的选择、转换效率以及扩展性作为自适应纠删码的评价指标。

3.2 比较与分析

3.2.1 码的选择

自适应码HACFS，HeART，Repair-Scale，SRS 和ERS 都是同一码族中的码之间转换，其转换效率高。但是同码族转换，无法避免码族的固有缺陷。比如RS 码的解码复杂度高，LRC码的存储开销大等。而LRC-HH 和MSR-RS 是不同码族中的码间转换，其能很好地避开各个码的缺点。比如MSR 码的编码复杂度高，解码复杂度低，而RS 码正好相反，二者的结合可以很好地避免码本身的限制。

3.2.2 转换效率

自适应是一项重要的任务，主要是因为自适应过程经常导致数据块重定位和奇偶块更新，这两种操作都会带来大量的I/O 成本。具体来说，传统的纠删码通常将块映射到一组固定的节点，这样，对象的数据块数量就等于存储对象数据的节点数量。如果自适应改变了数据块的数量（即k），则需要将一些数据块重新定位到不同的节点，从而产生额外的I/O。奇偶校验块的更新进一步加重了I/O：由于数据块的布局发生了变化，奇偶校验块需要相应的更新附加I/O，包括检索所有数据块以重新计算新的奇偶校验块，以及将新计算的奇偶校验块写入节点。现有的自适应纠删码都尽可能地避免了数据块重定向，但是校验块更新导致的I/O 开销和数据传输开销依旧很大。

3.2.3 可扩展性

现有的自适应纠删码只能在固定的参数之间变化，灵活性不够强，不能很好地适应时变的网络环境和不断变化的用户需求。故，如何根据网络环境，以及用户需求，做对应的自适应操作将是自适应纠删码的重要研究方向。

4 结语

本文对目前自适应纠删码做了比较全面的总结。首先介绍了纠删码的基本概念，随后介绍了基础的纠删码，接着详细介绍了现有主流的自适应纠删码。最后比较分析了这些纠删码的优缺点。我们认为，在当前自适应纠删码方法的研究中，进一步的研究重点主要包含两个方面：①提高转换效率。当前自适应码的转换效率较低，尤其体现在校验块的更新上，需要传输的数据块较多，这加重了纠删码的带宽开销，容易引发网络拥塞。故，有必要研究转换效率更高的纠删码。②提高扩展性。网络和用户需求具有时变性，灵活的纠删码能够更好地节省和权衡存储开销和通信开销。因此，研究扩展更为灵活的纠删码具有重要意义。