基于PSO-ELM的中国石油股票价格预测建模

钟 琳，颜七笙

(东华理工大学理学院，330013，南昌)

0 引言

股票投资常常伴随风险的发生,如何为金融投资者构建精度高且速度快的股市预测模型则有着积极的应用价值以及意义。

早期的股票预测主要是以传统时间序列、隐马尔科夫[1]模型等方法为主。其中ARMA模型[2]是时间序列中应用较为广泛的线性模型，何永沛[3]提出一种ARMA模型参数估计的改进算法，取得了较好的预测效果；孟坤[4]等运用ARMA模型对上证综合指数股票价格进行预测，结果表明ARMA模型较适合于进行短期预测。

然而传统的股票预测模型不能很好地解决非线性问题，学者们则提出了具有更好性能的支持向量机(Support Vector Machine, SVM)[5]、决策树[6]、人工神经网络等预测方法。郝知远[7]基于收益最大化，提出了一种遗传参数寻优的SVM算法，取得了较好的股价预测效果；Xiong[8]等人在传统的神经网络算法的基础上提出了LSTM算法，在对股票的实时预测与分析上取得了进一步的效果。

除此之外，组合模型预测方法也逐渐应用于股价的预测[9]。宋刚[10]等为提高股价预测精度，增强预测模型参数的可解释性，提出了自适应粒子群优化的长短期记忆的PSO-LSTM股价模型。綦方中[11]等则构建了一种基于PCA-IFOA-BP的股价预测模型，相比BP、PCA-BP和PCA-FOA-BP，预测精度更高。

极限学习机(ELM)是以前馈神经网络为基础构建的一类机器学习方法，广泛应用于各类预测问题[12]。相比传统的BP神经网络，ELM算法中的权值和阈值可随机生成，且不需在算法运行时调节，学习和达到稳定状态的速度快，极大地缩减了训练的时间，因其最优解是唯一的，故泛化性能也较好。

由于组合模型有着较高的预测精度以及ELM模型有着一定的优点，故本文采用粒子群优化极限学习机模型，对中国石油股票价格进行预测。并对PSO-ELM模型进行横向和纵向比较，相比ELM、PSO-BP、DE-ELM模型，判断各模型的优劣性，并将PSO-ELM进行短期、中期、长期预测，分析不同时期的预测效果。

1 数据和方法

1.1 数据描述

本文选取中国石油股票价格2010年11月1日至2021年1月29日共2 493条股票日交易数据作为实验样本，以收盘价、最高价、最低价、开盘价、成交金额5个影响因素为输入变量，次日收盘价为输出变量。各模型实验均将前2 218条样本数据作为训练集，后275条样本数据作为测试集。部分数据如表1所示。

表1 中国石油股票价格样本数据

1.2 基本方法

1.2.1 极限学习机 极限学习机算法中输入层与隐藏层间的权值及隐藏层的阈值可随机生成，且无需在训练时调节，只需确定隐藏层神经元个数，即可获得唯一最佳解，与传统的BP神经网络算法相比，其学习速度快，泛化性能好，从而被广泛应用于回归与分类。若训练样本R={(xj,tj)|j=1,2,…,m;xj∈Rn,tj∈Rm}则极限学习机的算法可表示为：

(1)

其中ωi=[ω1i,ω2i,…,ωni]T为输入层与隐藏层的权值，βi=[β1i,β2i,…,βmi]T为隐藏层到输出层的权值，g(·)为隐藏层激活函数，bi为隐藏层阈值，xj为输入值，tj为输出值，L为隐藏层节点数，N为样本数量。

式(1)可化简为

(2)

其中H为隐藏层输出矩阵，T为样本输出，β为输出层权值。

将训练集代入式(1)，计算隐藏层输出矩阵，即

(3)

通过式(2)和式(3)计算输出层权值β，即

(4)

式中H+是H的Moore-Penrose广义逆。

将测试集代入式(3)计算隐藏层输出矩阵H′，结合式(2)和式(4)，计算出测试集输出值，即

(5)

1.2.2 粒子群算法 粒子群算法(PSO)是群体智能优化中的一类算法，其在可行解空间里，初始化的粒子通过寻找个体极值Pbest和群体极值Gbest来更新个体速度和位置，粒子位置的更新伴随着适应度值的更新，通过比较更新前后粒子的适应度值，更新个体极值Pbest和群体极值Gbest的位置，依次下去，直到搜寻到最优解。

粒子速度和位置的更新公式如下

(6)

(7)

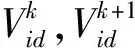
PSO具体的算法步骤如下。

1)粒子初始化及参数设置。在D维空间生成N个粒子群，初始化各粒子的速度和位置，其中第i个粒子的位置和速度分别为

xi=(xi1,xi2,…,xiD),1≤i≤N

vi=(vi1,vi2,…,viD),1≤i≤N

(8)

同时设置ω、c1,c2以及最大寻优次数等参数。

2)计算适应度函数值。通过适应度函数计算每个粒子的适应值。

3)将当前各粒子适应度与历史最优位置的粒子适应度相比，选择适应度更高(低)的位置并将其作为新的历史最优位置；同理将当前各粒子适应度与群体最优位置的适应度相比，并将所选位置作为群体最优位置。

4)更新粒子速度和位置。

5)更新适应度函数值、个体极值、群体极值。

6)判断算法是否符合算法结束条件。如符合，输出最优解和粒子；如不符合，则重回步骤3)～5)。

2 建立PSO-ELM股票价格预测模型

由于极限学习机的连接权值和阈值是随机产生的，在模型的训练过程中具有一定的不确定性，故针对中国石油股票价格预测问题，建立PSO-ELM股票价格预测模型，将粒子搜寻的最优解作为ELM权值和阈值的最优值，并在最优权值和阈值的基础上构建ELM预测模型。

具体建模过程如下。

1)归一化处理中国石油股票价格样本数据集，并将其分为训练集和测试集。

2)将训练集输入ELM模型中，得到ELM预测结果。

3)初始化PSO参数，各粒子表示ELM的权值与阈值，将ELM训练集的均方误差设为粒子群的适应度函数。

4)计算粒子当前最优位置pi的个体极值Pbest和全局最优位置pg的群体极值Gbest，以及第k个粒子位置pk对应的适应度gk：若gkPbest,则Pi=Pk,Pbest=gk,否则当前最优位置与个体极值不变；若gkGbest,则Pg=Pk,Gbest=gk，否则全局最优位置与群体极值不变。

5)根据式(6)、式(7)更新粒子速度和位置。

6)判断是否达到最大迭代次数。若满足，则算法继续；若不满足，则重复步骤4)～5)。

7)将最优粒子作为ELM的权值和阈值，将测试集输入ELM中，得到预测结果。

PSO-ELM算法流程如图1。

图1 PSO-ELM算法流程图

3 实验结果及分析

3.1 评价指标

为更好地评价模型预测效果，选择平均绝对误差(MAE)、平均绝对百分比误差(MAPE)、均方根误差(RMSE)以及拟合优度决定系数(R2)作为评价标准，各评价公式如下

(9)

(10)

(11)

(12)

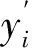
3.2 预测结果与对比分析

在MATLAB R2021a的环境下，基于中国石油股票价格数据，对PSO-ELM预测模型的精度进行测试，并对其预测效果进行分析。其中ELM输入神经元个数为5，隐藏神经元个数为5，输出神经元个数为1，隐藏层神经元激活函数选用sigmoid函数。部分PSO参数设置如下：种群大小设为20，最大迭代次数k为300，学习因子c1=c2=2，惯性权重ω按式(13)计算

(13)

其中ws=0.9,we=0.4,T,k分别为迭代次数和最大迭代次数。PSO-ELM预测结果如图2、图3所示。

由图2、图3可知，PSO-ELM模型的拟合优度决定系数为R2=0.974 81，预测值与实际值较为符合，其价格走势相同，适应度函数值收敛较快，均方根误差RMSE=0.12 738较小，预测效果较好。

图2 测试集日收盘价格预测结果(PSO-ELM)

图3 PSO-ELM适应度曲线

为进一步比较模型的预测效果，选取ELM,PSO-BP,DE-ELM模型作为参照比较分析，其中PSO-BP模型将BP训练集的均方误差作为适应度函数，DE-ELM的种群也设为20，最大迭代次数为300，各模型其余的参数均依照PSO-ELM的方法设置，模型的预测对比图如图4～图9所示。

图4 测试集日收盘价格预测结果(ELM)

图5 ELM误差曲线

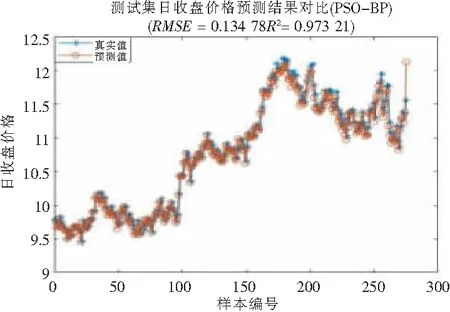
图6 测试集日收盘价格预测结果(PSO-BP)

图7 PSO-BP适应度曲线

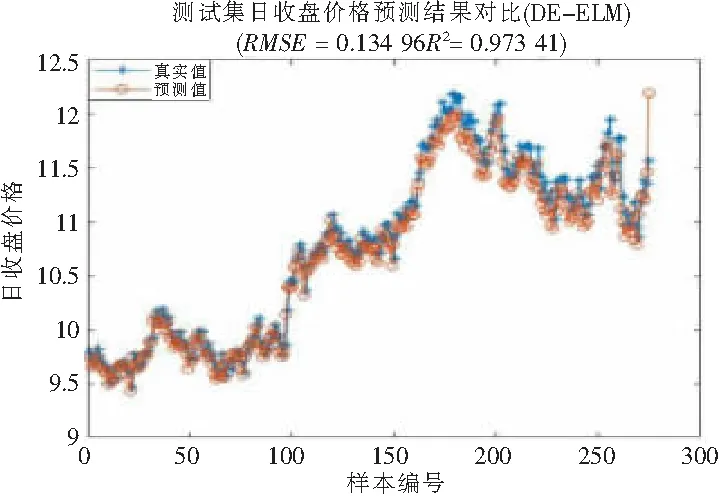
图8 测试集日收盘价格预测(DE-ELM)

图9 DE-ELM适应度曲线

由以上各个模型的预测结果及其适应度曲线可以看出，ELM、PSO-BP、DE-ELM模型预测效果也较好，但相比PSO-ELM模型，各模型的预测曲线没有PSO-ELM模型吻合，从均方误差RMSE和拟合优度决定系数R2来看，PSO-ELM模型在4个模型中均为最优。此外，PSO-ELM和PSO-BP的适应度曲线较DE-ELM来说收敛较快，其在迭代次数不到100时就达到稳定，而DE-ELM在迭代约275次后逐步稳定，速度较慢。

为更为直观地比较预测效果，各模型的评价指标值如表2所示。

表2 各模型评价指标对比值

从各模型的均方误差RMSE来说，PSO-ELM模型相比没有经过参数寻优的ELM模型降低了1.84%，相比PSO-BP、DE-ELM分别也降低了1.07%、0.97%，可见通过粒子群算法对极限学习机的参数寻优有一定的效果，以及相比BP算法，ELM算法有一定的优越性，且粒子群算法较差分进化算法寻优效果更好；PSO-ELM模型的MAE、MAPE相比其他3个模型的值均较小，则说明PSO-ELM模型预测值误差更小，并且有着更好的预测精度；从R2来看，PSO-ELM模型的拟合优度决定系数达0.974 3，相比其他模型分别提高了0.75%、0.08%、0.09%，说明PSO-ELM模型有着较高的拟合度，预测效果有所提高。

3.3 PSO-ELM不同时间长度的预测效果比较

为了验证PSO-ELM模型对不同时间长度的预测效果，选取中国石油股票价格样本分别进行短期(2021.02.01—2021.02.05)、中期(2021.03.15—2021.03.19)、长期(2021.04.26—2021.04.30)预测。预测结果如表3～表5所示。

由表3～表5计算可知，短期、中期、长期的平均相对误差分别为2.748 4×10-3、1.053 6×10-2、1.204 4×10-2，由此表明PSO-ELM模型适合短期预测，随着时间长度的增加，平均相对误差值也在增加，预测的精度在降低，因此，建议股票投资者尽量依据近期样本来预测最近几天的股价涨跌，从而提高股票价格的预测精度，依据预测的股价走势来做出决策，以此避免产生较大的投资风险和损失。

表3 真实值与预测值对比(短期)

表4 真实值与预测值对比(中期)

表5 真实值与预测值对比(长期)

4 结束语

本文为提高股票价格预测的精度，基于中国石油股票价格数据，提出了粒子群优化极限学习机的PSO-ELM模型，该模型通过粒子群位置和速度的更新逐步搜索最优适应度值，同时将粒子群中搜索到的最优解作为ELM的权值和阈值，再对测试集进行预测。通过对PSO-ELM模型横向比较，也即与ELM、PSO-BP、DE-ELM模型的预测效果对比，结果表明PSO-ELM模型拟合效果较好，预测精度较高。

除此之外，再对PSO-ELM模型进行纵向比较。通过选取不同时间长度的股票价格，分为短期、中期、长期进行预测，结果表明短期预测的平均相对误差小于中期和长期的。因此，PSO-ELM模型较适合于对短期股价进行预测，同时也建议股票投资者尽量依据近期样本来预测最近几天的股价涨跌，从而提高股票价格的预测精度，避免产生较大的投资风险和损失。