课程思政背景下的复合函数求导*
陈小燕 秦勇 梁素梅
(云南机电职业技术学院)
复合函数求导是导数与微分章节的重难点内容,是导数计算中的“桥梁”,上接一般函数的导数计算,下连“隐函数、幂指函数、参数方程确定的函数”三大函数的导数计算。若复合函数导数计算未掌握,便在高等数学的学习中形成了阻碍,其难度打击了不少学生学习高等数学的积极性,故而复合函数求导也是高等数学授课教师多年来积极探讨的内容之一。笔者于2021年11月19日在知网上以“复合函数导数”为主题进行搜索,搜索到586条记录,其数量接近“高等数学课程思政”的两倍,本文是在高等数学课程思政实施的背景下,对复合函数求导的一种新的教学尝试。
一、高等数学课程思政介绍
“课程思政”于2014年在上海被提出,是指将思想政治教育贯穿于教育、教学全过程,将思想政治教育融合于通识课、专业课教学中,与思想政治理论课同向同行,实现全员、全程、全方位育人,从而达到立德树人目的。
云南机电职业技术学院于2019年开始课程思政建设,分三批立项,迄今共建25门课程思政,既有公共基础课、也有专业课,高等数学课程思政项目于2020年立项,迄今实施课程思政教学1.5个教学周期。在我院的高等数学课程思政教学中,项目组组建了融合式教学团队,将思政教师纳入团队,负责团队的思想政治理论培训和案例的思想意识把关,团队制定了课程思政的授课计划和教案,明确了“教什么”“怎么教”,充分挖掘了高等数学课程中的思想政治元素,在教学设计中做到了“两结合一贯穿”,即将数学知识的传授和价值引领相结合,将培育和践行社会主义核心价值观与培养具有工匠精神的技能人才相结合,将中华民族优秀传统文化、数学文化贯穿始终截至目前,团队研讨开发课程思政案例十余例,录制课程思政授课视频数段,充分利用网络资源,采用线上线下混合式教学,经问卷星调查,学生对引入的思政元素满意度、对教师的教学满意度达到88.5%,提高了高等数学课程的教学质量。
二、课程思政背景下复合函数求导教学设计
复合函数求导是导数计算中的重难点内容,是学生学习高等数学的一大阻碍,此重难点内容打击了部分同学的学习积极性。故而,笔者在本章节的教学设计中引入了坚持不懈、攻坚克难的科学家故事,引导同学们锲而不舍、迎难而上,培养同学们勇于尝试和探索的科学研究精神;笔者在本章节的教学实施中分析了复合函数求导公式的逻辑性和对称性,引导同学们发现数学中的美,一定程度上疏导了同学们的焦虑心情,培养同学们自主学习的能力和分析问题、解决问题的能力。在本章节的教学中,笔者采用双螺旋式教学,数学知识的传授和对综合素质能力的培养双线并行。在教学设计中,根据学生情况制定教学目标,确定“教什么”“怎么教”,在教学过程中使用“引、思、论、探、测、评”6个环节,具体设计流程如图1。

图1 教学设计流程

图2 教学方法分析
(一)摸清学生情况,教学设计有理有据
在我院,《高等数学》课程仅针对大一学生开设,大一学生对本课程的学习具有一定的积极性,00后的大学生喜欢使用手机进行学习,已习惯登录智慧职教平台进行学习,为混合式教学提供了条件;复合函数求导位于导数的四则运算法则之后,在此之前,学生已掌握一般函数求导的方法,已具备对复合函数求导的基础。但我院学生文理方向均有,学生的数学基础参差不齐,对于数学概念、定理的理解能力不一样,多数同学在学习上有畏难情绪,部分同学缺乏自主学习的积极性和独立思考的能力。
(二)分析教学目标,明确本章节教学重难点,确定“教什么”
根据教材内容和学生情况,在复合函数导数章节的教学中,知识目标方面要使学生理解链式法则;技能目标方面要提高学生对数学概念、定理的理解能力,掌握复合函数的求导方法;素质目标方面要培养学生不畏艰难、勇于尝试和探索的科学研究精神,进而提高学生的综合素质。其教学重点为链式法则的使用,其难点内容为复合函数求导。
(三)设计教学方法,明确“如何教”
经日常教学观察和数据收集发现,学生在进入复合函数导数学习时,有前后内容衔接不顺利、畏难情绪过重、对数学定理理解不到位、课时紧张等问题,故笔者在此章节采用了问题驱动法、线上线下混合式教学、类比教学法等教学方法。
(四)紧抓“引、思、论、探、测、评”六环节实施教学(见表1)
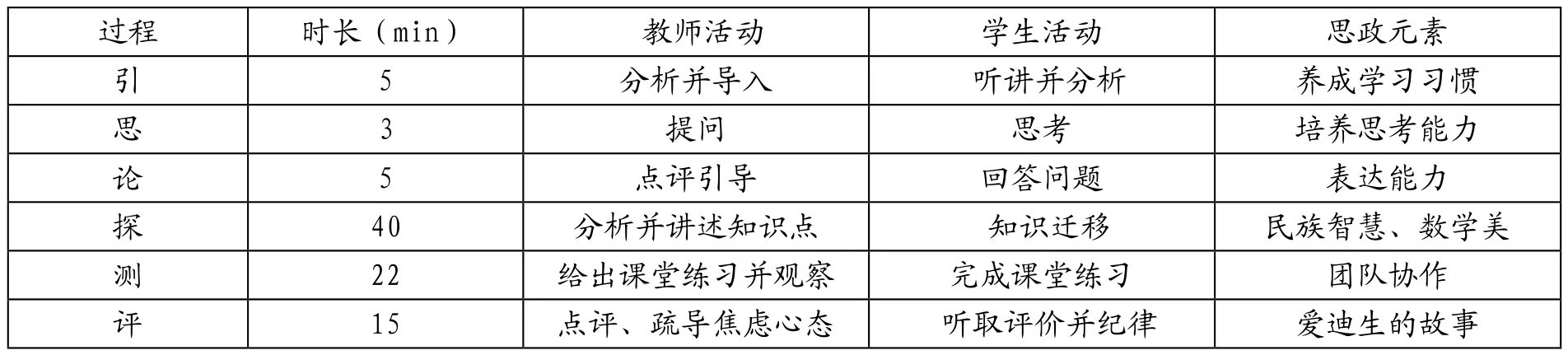
表1 课程思政背景下复合函数求导的教学实施
1.引:教师从课后作业和平台课前测验的情况,总结导数四则运算掌握的情况;利用的导数,对比与得出本章节的授课内容;要求学生聚精会神听课,跟随授课教师的步伐,总结前次课内容,分析个人的不足之处。 在对作业和测验的分析中,展示优秀样本,并强调要逐步形成好的学习习惯。
3.论:教师请2-3人回答问题,点评,然后与学生一起讨论上述问题,概括结论,引出复合函数求导法则;学生回答问题,在老师引导下讨论上述问题。
4.探:教师讲述曹聪称象的故事,启发学生得出曹聪称象的方法,并将此方法迁移到复合函数求导中,以此得到复合函数求导的链式法则,引导学生归纳总结其四个步骤并讲解例题。学生根据老师的讲述主动进行知识迁移,理解复合函数求导的链式法则,掌握其求解步骤,记录笔记;通过对曹聪象故事和链式法则的讲解,将中国古人的智慧和数学的逻辑美、对称美进行展示,增强大家的民族自豪感,激发大家的学习积极性。
5.测:教师给出课堂练习题,观察学生练习情况,给予适当提示和纠正;学生完成课堂练习,进行汇报;通过课堂练习,让学生体验团队合作提高团队协作能力。
6.评:教师通过对练习情况的观察和练习结果的考察,利用科学家的故事疏导同学们的畏难情绪,评价各个小组团队合作的情况和复合函数求导链式法则的掌握情况,布置课后作业,简要提出下次课的学习任务;学生听取老师评价,做笔记,针对自身情况进行总结;通过科学家故事的讲解,引导大家克服畏难情绪,严格按照四个步骤,逐步掌握复合函数求导方法。
(五)做好教学反思,总结经验再出发
本章节是导数计算中的重难点内容,故设计用4学时来完成教学,另在线上平台还上传了课前预习视频、课后复习视频和课后测验。经个别交流、平台互动和个人反思可见,在本章节的教学中还存在课堂教学中讲解过长、留给同学思考的时间不足、未充分利用平台数据、与实际生活关联性不高等问题,在后期的教学实施中,将在上述方面进行改进。
三、课程思政案例
在以往教学过程和个别交流中发现,在复合函数求导章节中,个别同学畏难情绪重,其难度也打击了部分同学的学习积极性,使其在思想上形成了一定压力,进而抗拒学习。所以,在本章节的课程思政建设中引入了科学家不畏艰难、百折不挠的故事,帮助同学们重拾信心再出发;还引入了曹聪称象的故事,帮助学生理解复合函数求导方法。
(一)有100次跌倒就有101次的爬起的爱迪生
托马斯·阿尔瓦·爱迪生,世界著名的发明家、物理学家、企业家,被誉为“世界发明大王”,拥有重要的发明超过2000项,他发明的留声机、电影摄影机和电灯对世界有极大影响。其实,爱迪生发明创造的过程并不是一帆风顺的,而是屡败屡试、总结经验再试验的过程。他在研制电灯的过程中经历了上万次的失败。1878年9月,爱迪生决定向电力照明这个堡垒发起进攻,他决心制造出价格便宜、经久耐用,而且安全方便,普通百姓也能用的电灯。他先后用炭丝、白金、钡、钛、锢等接近1600种材料进行了上万次的试验,但都未达到理想状态,但爱迪生并未灰心,而是不断总结经验、不断试验,终于在1879年10月21日,找到了可以连续发热发光45个小时的材料,这是人类第一盏有广泛实用价值的电灯,灯丝用碳化棉丝制成。但爱迪生并不满足于此,而是为延长灯泡寿命而继续研究。最后,爱迪生找到了竹这种植物,把炭化后的竹丝装进玻璃泡,通上电后,这种竹丝灯泡竟连续不断地亮了1200个小时。到了1906年,爱迪生又改用钨丝来做,使灯泡的质量又得到提高,被一直沿用到今天。
所以,在学习和工作中,困难不可怕、失败也不可怕,失败乃成功之母,我们要像爱迪生一样,学会思考、善于总结,有100次跌倒,就有101次爬起,总结经验再出发,成功就在不远处。在复合函数求导的过程中也一样,我们要不怕困难,勇于挑战,重视积累,一步一个脚印,逐步解决复合函数求导中的重难点问题,最终掌握复合函数求导这个知识点。
(二)“化整为零”的称象思想
曹冲生五六岁,智意所及,有若成人之智。时孙权曾致巨象,太祖欲知其斤重,访之群下,咸莫能出其理。冲曰:“置象大船之上,而刻其水痕所至,称物以载之,则校可知矣。”太祖悦,即施行焉。曹聪称象的方法,就是典型的化整为零思想和类比转化思想。古时候,没有能称象的工具,曹聪就用类比转化思想,先记录象站在船上水平面达到的高度,然后在船中放入石头。当水平面上升到相同的高度时,船内石头的重量和象的重量就是一样的;然后,又用化整为零的思想,一部分一部分地称石头的重量,最后,将所有重量加起来,就是象的重量。实际上,复合函数的导数也是如此,整个复合函数导数很难求解,那么,我们便化整为零,将复合函数分割成几部分,然后一部分一部分求导,最后再合起来。
在本章节引入曹冲称象的故事,一是向大家介绍中国古人的智慧,增强大家的民族自豪感,激发学生的学习积极性;二是以实际例子说明数学来源于实际生活,服务于实际生活,建立“数学有用论”,增强学生学习主观能动性;三是用类比转化法得出复合函数求导的方法“化整为零”—链式法则,并以链式法则体现数学蕴藏的对称美、逻辑美,帮助大家克服畏难情绪,舒缓紧张心情。
四、教学成效
通过课堂教学的观察、课堂练习、课后作业、测验和个别交流的反馈,在复合函数求导环节引入思政元素,达到了以下教学效果:
一是有效激发学生学习兴趣,降低畏难情绪,提升学习主观能动性,树立自信心。授课教师在课堂上讲解爱迪生发明之路的故事后,让同学们明白了“世上无难事,只要肯攀登”,失败是成功的垫脚石,失败也是一种宝贵的经历,同学们在学习上的畏难情绪明显降低。授课教师在课堂讲解曹聪称象的故事,让同学们体会到了数学思维的重要性,激发了学习数学的兴趣,学习的主观能动性得以提升。
二是有效拉近师生距离,高等数学不再“高冷”。授课教师在课堂上进行思想政治教育后,同学们体会到了老师的人文关心和关怀,拉近了师生之间的距离;通过对曹冲称象故事的分析,让同学们体会到高等数学思想与实际生活的联系,使高等数学不再“高冷”。
三是有效提高教学质量。通过课堂练习、课后作业和测验发现,引入了思政元素的复合函数求导后,同学们更易理解和掌握复合函数求导方法,高等数学其它知识点亦是如此。据统计,2018—2019学年上学期本教学团队授课班级的及格率为84.14%,分数在90及以上的达5.08%;2019—2020学年上学期本教学团队授课班级的及格率为87.67%,分数在90及以上的达6.27%;2020—2021学年上学期本教学团队授课班级的及格率为89.84%,分数在90及以上的达9.6%,可见同一时期的及格率稳步上升,教学质量明显提升。
经广大学者研究和本教学团队的教学实践证明,在高等数学课程中融入思政元素是一种行之有效的方法,在复合函数求导环节引入思政元素,可以有效激发学生的学习兴趣、有效对抗畏难情绪、有效拉近师生距离、有效树立学生信心、有效提高教学质量,达到高等数学的育人功效。

