淤泥质海底航道边坡失稳程度评估与预测*

范园园，张存勇，成 玮

(江苏海洋大学 海洋技术与测绘学院，江苏 连云港222005)

淤泥质海底航道多为人工开挖航道，边坡可挖性好，极易受波浪和潮流动力的影响发生失稳、滑塌现象[1]。航道一旦发生失稳滑坡不仅会改变航道水深影响正常航运，还可能造成航段淤浅，影响港口的运营与发展[2]。由于海底航道边坡的特殊性，无法直接对边坡稳定性进行监测，大多数海底边坡不稳定性研究局限在边坡发生失稳、滑塌之后[3]，很少有对航道边坡失稳程度进行预测研究。为保障过往船只安全通行、完善航道维护管理，急需对淤泥质海底航道边坡失稳程度进行评估预测。

由于淤泥质海域海水特性限制了水下光学成像技术、电磁波传播探测技术在航道边坡监测中的应用，而声波在海水中具有较强的穿透力和相对较小的衰减，因此声波探测技术被广泛应用在海底沉积物探测中[4]。另外，航道边坡失稳、滑塌具有不确定性，无法利用声波探测技术在现场获取失稳、滑塌全过程声纹数据，因此采用工程试验模拟的方法在水槽内模拟航道边坡失稳滑塌全过程，同时利用浅地层剖面仪记录并获取航道边坡失稳、滑塌全周期地层剖面声纹图像，基于声纹图像开展淤泥质海底航道边坡失稳程度评估预测研究。声纹图像特征提取是正确评估航道边坡失稳程度的重要环节[5]，为了研究图像纹理特征，众多学者提出了各种不同的图像处理算法，包括小波变换[6]、二维Gabor滤波[7]、灰度共生矩阵[8]、局部二值模式[9]等，其中Gabor变换参考了心理学与生理学研究，可以增强纹理图像在不同方向不同尺度的特征，对纹理特征的描述与人的视觉神经感受高度相似[10-11]。因此本文通过Gabor变换提取声纹图像特征，利用离散余弦变换对Gabor特征进行降维处理，以此构建淤泥质海底航道边坡失稳程度评估预测模型。

1 材料与方法

1.1 室内试验

利用在连云港淤泥质航道采集的航道边坡沉积物在室内水槽模拟航道边坡失稳滑塌过程，通过浅剖探测技术获取淤泥质海底航道边坡失稳滑塌全周期声纹图像。设计一个边坡，坡顶至水泥槽底130 cm、坡长118 cm、坡度45°，将换能器固定在轨道上，与主机相连接，换能器距坡顶50 cm。设置初始声速1 600 m/s、频率15 kHz，利用浅地层剖面仪向航道边坡发射声波、接收回声，对接收的声波数据进行去噪处理，形成具有一定灰度的点状、线状和块状图形组成的浅地层剖面声纹图像[12-13]。

1.2 Gabor变换

Gabor变换是Gabor提出的用于描述图像纹理特征的技术，它可以同时保留图像空间域和频率域信息，在图像局部特征增强和频域信息采集中都有良好的效果，在空间域中，Gabor变换为带通滤波器，使用三角函数与高斯函数叠加便可得到一个Gabor滤波器[14-15]，其表达式为：

(1)

x′=xcosθ+ysinθ

(2)

y′=-xsinθ+ycosθ

(3)

(4)

式中：G为Gabor滤波器空间函数；(x，y)为图像像素点位置；λ为Gabor滤波波长；θ为Gabor核函数方向；ψ为相位偏移；σ为Gabor核函数标准差；γ为长宽比。其中γ决定Gabor核函数的形状，σ由波长λ与式(4)中宽带b共同决定；(x′，y′)由(x，y)旋转θ得到。

1.3 Fisher判别

Fisher判别法是Fisher在方差分析的基础上提出的用于总体分类的方法[16]。其主要原理是将高维空间的数据点投影到低维空间，通过构建线性判别式对总体样本进行分类。

假设一共有K类总体G1，G2，…，GK，从每一类总体中各抽取N1，N2，…，NK个样品，每个样品中包含P个判别因子。设判别函数为：

y(x)=c1x1+c2x2+…+cpxp

(5)

式中：(c1，c2，c3，c4，…，cp)为Fisher判别式判别系数；(x1，x2，x3，x4，…，xp)为样品的p个判别因子。

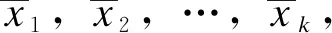
(6)

(7)

根据判别思想构造：

(8)

式中：λ为A0矩阵的特征根；c为特征根对应的特征向量。矩阵特征根λ不止一个，因此可以得到多组Fisher判别式判别系数，构建多个判别式。把特征根λ按从大到小排序，将每个特征根与所有特征根之和的比值作为判别式的判别能力，对判别式进行筛选。对于待判样本，根据样本函数值与各类中心函数值空间距离进行航道边坡失稳程度预测评定：

(9)

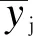
2 结果与分析

2.1 失稳程度评估

由于航道边坡失稳滑塌全周期声纹图像的连续性，无法确定失稳阶段和各失稳阶段界限，因此将全周期声纹图像裁剪为m×n的图像矩阵，共计150张，根据声纹图像能量变化对航道边坡失稳程度进行评估。声纹图像是对剖面仪回波信号进行处理转化而来，采用能量特征作为航道边坡失稳程度评估依据，不仅能在图像层面直接反映声强变化规律和纹理的粗细均匀度，还可以间接表示声波反射剧烈程度，能够更直观、准确地表示航道边坡失稳滑塌过程，因此本文根据声纹图像能量特征变化ASM对航道边坡进行失稳阶段划分：

(10)

式中：L为图像像素的大小；i、j表示灰度值；p(i，j)为灰度共生矩阵的归一化值。

从图1可以发现，随着航道边坡失稳加剧，能量变化曲线整体表现为先增后降的趋势，说明航道边坡失稳滑塌是一个能量耗散与积聚的过程。根据能量特征变化曲线将其失稳滑塌过程划分为5个阶段：非常稳定、稳定、不稳定、极不稳定、滑塌。随着航道边坡失稳滑塌的进行，能量逐渐减少，在极不稳定区域能量跌至最低，此时航道边坡能量几乎耗尽，不足以支撑其稳定结构，即将发生失稳滑塌。发生失稳滑塌之后，航道边坡向着稳定方向发展，能量重新积聚，滑塌造成的能量损耗导致航道边坡再次稳定之后的能量明显减少。

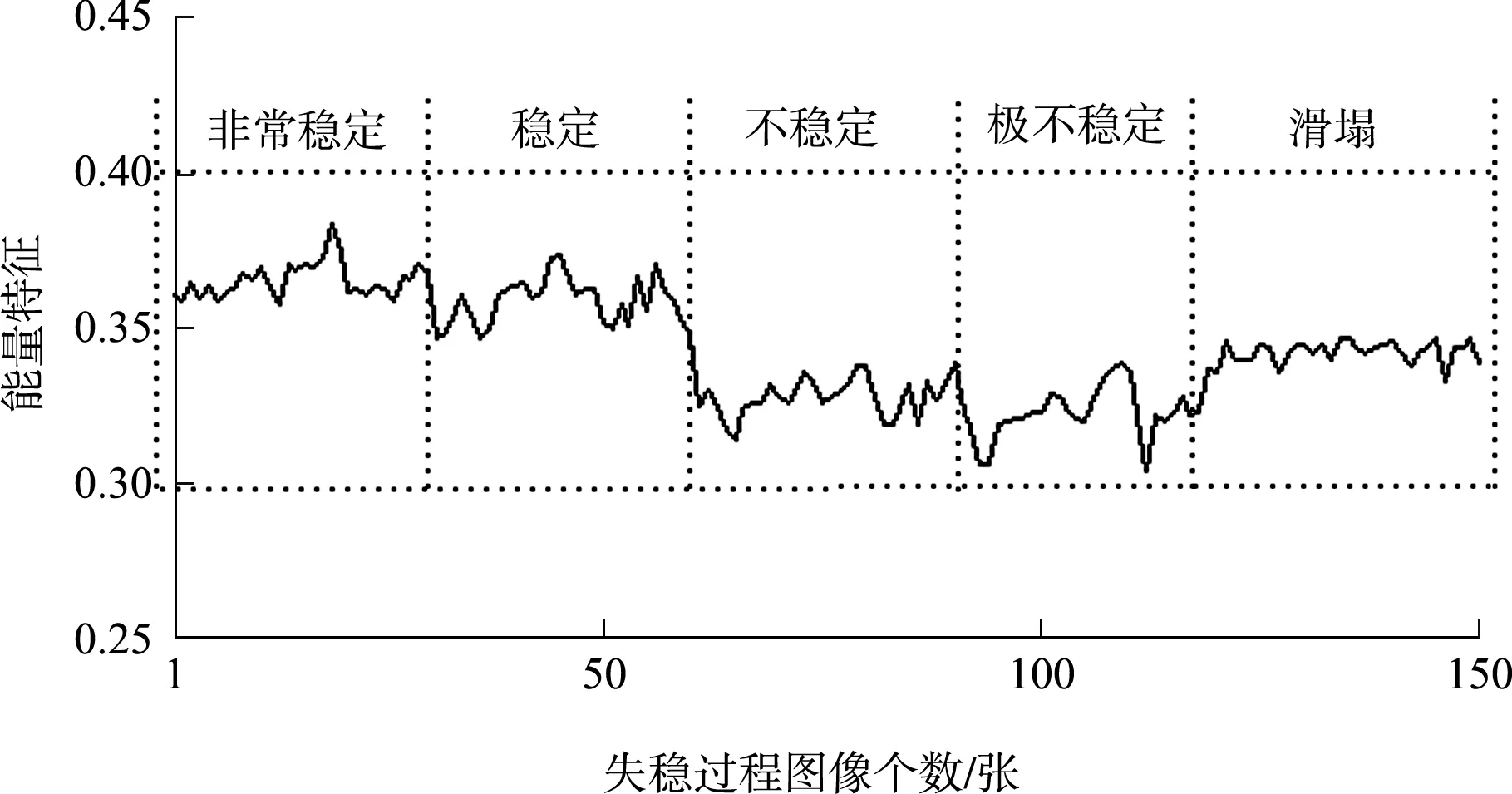
图1 航道边坡从稳定到滑塌声纹图像能量变化曲线

2.2 Gabor滤波处理

分别从5个失稳阶段中随机挑选20张共计100张声纹图像作为特征提取和失稳程度评估预测模型构建的原始样品，其余50张声纹图像作为待判样本用于检测模型预测准确性，图2所示为淤泥质海底航道边坡不同失稳阶段声纹图像样本。

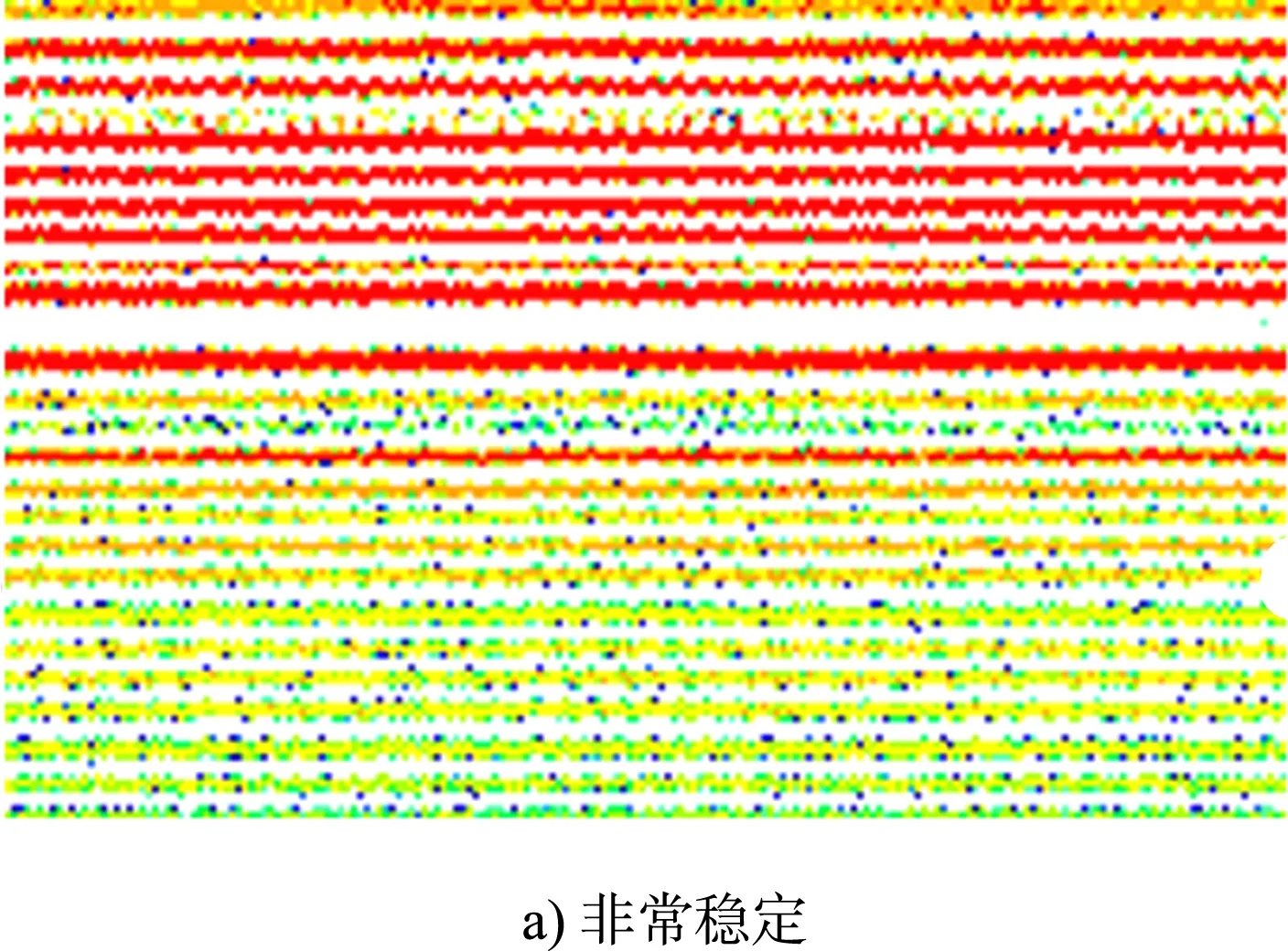
图2 淤泥质海底航道边坡不同失稳阶段声纹图像样本

为充分利用有效声纹图像特征，首先要选取最优Gabor滤波器参数对声纹图像进行Gabor变换，然后利用离散余弦变换(DCT)对Gabor特征做降维处理，选出最具有代表性的纹理图像信息作为构建航道边坡失稳程度评估预测模型的最终特征。

2.2.1Gabor滤波器设计

选择合适的滤波器，设计合理的滤波参数是决定航道边坡失稳程度评估、预测模型预测准确率的重要环节。从式(1)可以知道，Gabor滤波函数由实部和虚部两部分组成，在实际使用过程中，为简化计算流程，提高滤波效率，通常选择实部与虚部二者之一进行Gabor滤波。Gabor滤波函数的实数部分作为一个偶对称滤波器在特征提取方面效果更好，因此选择Gabor函数实部对声纹图像进行滤波处理：

(11)

对于波长λ、方向θ、相位偏移ψ、长宽比γ、宽带b等滤波器参数采用控制变量法择优选取。Gabor幅值特征中包含着图像的能量信息，通过计算不同阶段声纹图像Gabor特征幅值之和，找出与图1能量变化规律相同且5个失稳阶段层次清晰、阶梯变化明显的曲线，即可找到Gabor滤波器最优参数。分别从5个失稳阶段中选出1张代表此阶段的声纹图像，通过不断调整某一参数值同时保证其余参数不变的情况下，对5张声纹图像进行Gabor滤波处理，通过分析幅值之和变化曲线确定最能表示声纹图像特征的Gabor滤波参数。经过反复试验确定Gabor滤波参数取值范围，然后选择合理步长对声纹图像进行处理，得到一组最优参数(表1)。

表1 Gabor滤波器参数取值范围

利用上述方法最终确定在λ=4、θ=0°、ψ=30°、γ=0.4、b=1.5时Gabor滤波器提取的声纹图像特征效果最好，最符合航道边坡失稳滑塌过程。图3为最优参数下Gabor滤波器滤波过程示例，得到Gabor幅值特征变化曲线见图4。

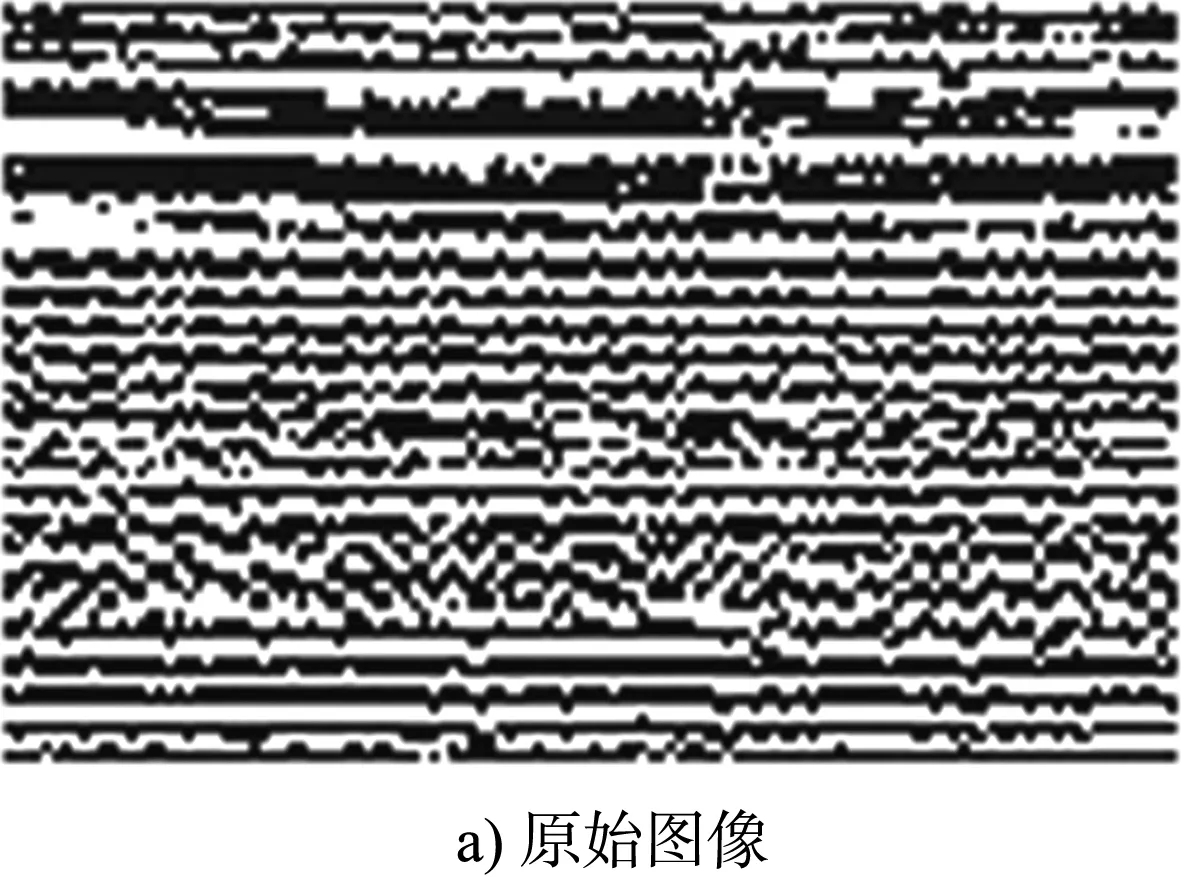
图3 最优参数下Gabor滤波器滤波过程

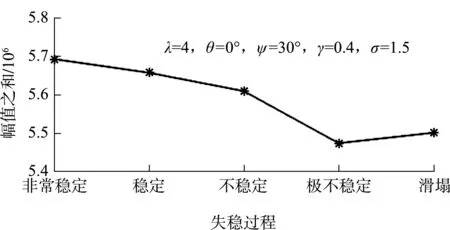
图4 Gabor函数最优参数下滤波图像幅值之和变化曲线

2.2.2DCT特征降维

声纹图像进行Gabor滤波后仍为图像特征矩阵，矢量维数复杂，不利于后续失稳程度评估预测模型构建，因此要对Gabor特征进行降维量化，提取主要特征信息，减少运算量。离散余弦变换(DCT)具有“能量聚集性”，对其进行特征降维不仅能够保留原始数据的重要信息，还能加快运算速度提高效率。Gabor特征经过二维离散余弦变换后，系数之间的相关性会降低，能量集中在左上角位置[17]。因此通过提取二维离散余弦变换图像左上角h×h的主成分即可达到特征降维的目的。

图5 DCT特征降维原理

2.3 Fisher模型构建

根据Gabor特征降维后所选取的主成分范围不同，组建的判别因子也不一样，对于后期预测模型识别准确率会产生影响，因此选择不同的判别因子对其判别能力进行验证。结果见表2，判别能力基本集中在前4个判别函数中，因此将4×4、5×5、6×6的主成分特征作为判别因子，分别构建2、3、4个判别模型，采用回代估计的方法将100张声纹图像样品特征输入到函数模型中，依据识别正确率选择最佳判别模型。

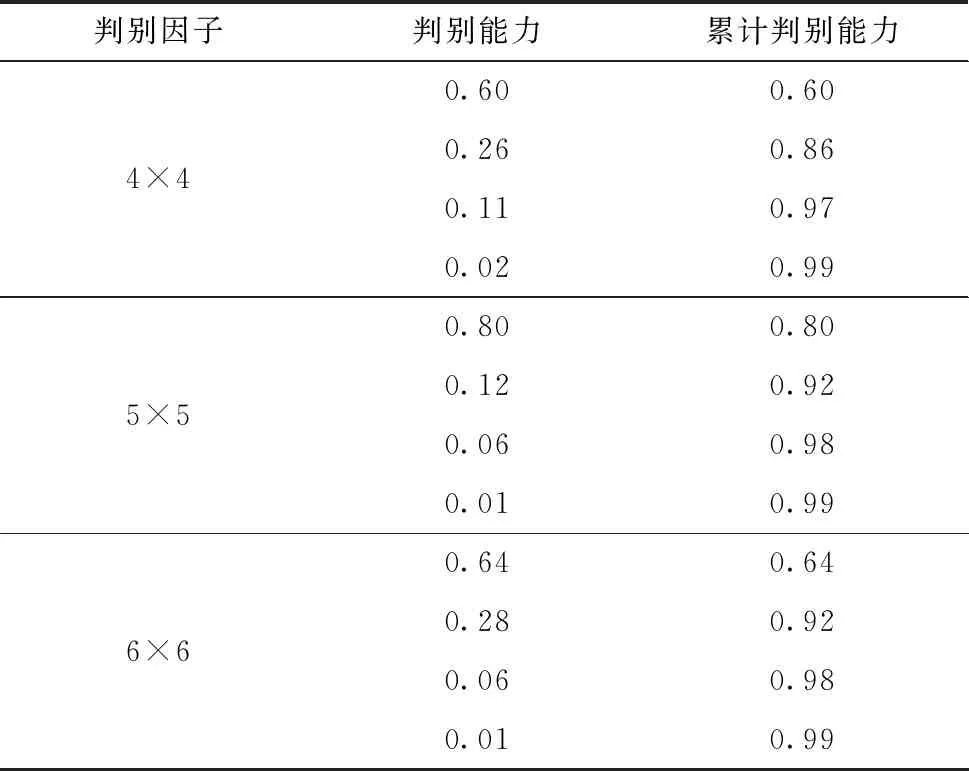
表2 不同判别因子下判别式判别能力

从表3可以发现，随着主成分选取的不同，判别函数识别准确率也不同。为了提高运算效率，减少计算量，最终选择6×6的主成分特征构建3个Fisher判别式对航道边坡失稳程度进行评估预测。其中各类函数中心值为：非常稳定(13 226.28，9 334.72，6 968.35)、稳定(11 910.54，10 923.34，7 558.33)、不稳定(11 685.07，10 982.79，6 561.49)、极不稳定(9 996.11，9 618.05，6 993.31)、滑塌(12 179.80，10 711.11，6 792.01)。

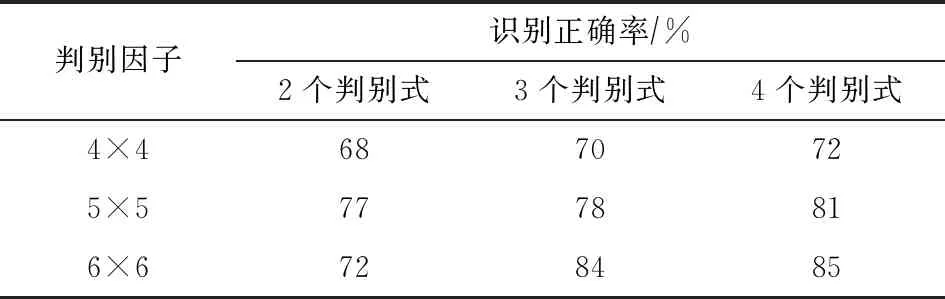
表3 样本回代估计识别正确率

将50张待判样本的36维特征输入到Fisher预测模型中，采用式(9)的方法对样本失稳程度进行评估预测，结果识别错误数5个，总体识别准确率达90%。

3 结论

1)随着航道边坡失稳滑塌的进行，声纹图像能量逐渐递减，边坡发生失稳滑塌之后能量有所回升，说明航道边坡在水动力作用下能量逐渐损耗，直到剩余能量不足以支撑其稳定结构发生失稳滑塌。失稳之后，由于滑塌造成能量损耗，因此边坡再次稳定后的能量远不如初始稳定结构。据此将淤泥质海底航道边坡失稳滑塌过程划分为：非常稳定、稳定、不稳定、极不稳定、滑塌5个阶段。

2)对声纹图像进行Gabor-DCT特征提取发现在λ=4、θ=0°、ψ=30°、γ=0.4、σ=1.5时Gabor滤波器滤波效果最好，得到的声纹图像特征最符合航道边坡失稳滑塌过程，基于DCT对Gabor特征降维处理，依据预测模型识别准确率得出在6×6的区域主成分包含了声纹图像的主要特征信息。

3)通过回代估计法将100张声纹图像的36维特征输入Fisher预测模型，识别准确率为85%。利用6×6判别因子构建3个Fisher判别式对50张声纹图像待判样本失稳程度进行评估预测，识别准确率为90%。