裂隙砂岩破坏过程中的能量耗散与破碎分形特征研究

刘享华 张科 吴文远

摘要：对不同裂隙倾角的裂隙砂岩试件进行单轴压缩试验，分析了试件变形破裂过程中的应变能演化特征，基于分形理论定量描述了最终破坏后碎屑尺度分布的分形特征，初步探究了能量耗散与破碎分形维数之间的力学机制。研究结果表明：随着裂隙倾角增加，裂隙砂岩试件的抗压强度和耗散应变能均呈现出先减小后增大的变化规律;数据拟合结果表明两者之间存在正相关关系。试件破坏后的碎屑尺度分布具有分形特征，不同裂隙倾角试件的分形维数介于2.58～2.64;分形维数随裂隙倾角的变化规律与抗压强度类似，两者近似呈线性相关关系。此外，试件的抗压强度越高，破坏时释放的耗散应变能越多，试件破碎程度越严重，所产生的微、细粒碎屑占比增大，导致分形维数变大;数据拟合结果表明耗散应变能和分形维数之间具有线性正相关关系。

关键词：岩石力学;裂隙倾角;能量;抗压强度;破碎;分形维数

中图分类号：TU45

文献标志码：A文章编号：1000-582X（2022）02-041-11

Abstract： This paper aims to investigate the correlation between the energy dissipation and fractal characteristics of fragments of preflawed sandstone. First， the uniaxial compression tests on preflawed sandstone with different flaw inclinations were conducted to analyze the energy evolution characteristics of preflawed sandstone during loading. Based on fractal theory， the size distribution characteristics of fragments after final failure were quantitatively characterized. The study shows that the compressive strength and the dissipation strain energy of specimen first decrease and then increase with the increase of flaw inclination and the data fitting suggests a positive correlation between them. The fragment size distribution of fragments under the uniaxial compression tests has obvious fractal property. The fractal dimensions of specimens with different flaw inclinations are in the range of 2.58-2.64. The trend of fractal dimension changing with flaw inclination is similar to that of compressive strength， and fractal dimension and compressive strength are approximately linearly related. The higher the compressive strength of the specimen is， the more the dissipative strain energy releases during failure. At this time， the more severe failure the specimen has， the greater the proportion of micro and fine particles is， resulting in the increase of fractal dimension. The regression analysis shows the relationship between dissipation strain energy and fractal dimension is linear positive correlation.

Keywords： rock mechanics; flaw inclination; energy; compressive strength; fragmentation; fractal dimension

物質破坏是能量转化作用下的一种状态失稳现象[1]。岩体受载变形并破坏实质上是不可逆的热力学过程，能量的耗散和释放至关重要[2]。因此，从能量转化作用角度研究岩体破裂机制得到众多学者的青睐[3-7]。

目前，不少学者从热力学的角度研究了岩石的破坏机制，并取得了一系列的研究成果。在单轴压缩条件下，孟庆彬等[3]研究了不同应变率加载条件对岩石破坏过程中能量积聚和耗散的影响规律。王伟超等[4]基于能量耗散理论发现盐岩破坏过程中的能量与应变关系曲线表现出明显的阶段特征，可分为压密、弹性变形、塑性变形和破坏4个阶段。Chen等[5]建立了描述砂岩裂缝闭合效应的裂缝闭合能量耗散模型，并发现以此计算得到的砂岩裂缝闭合等效弹性模量与高径比呈非线性递减关系。Zhang等[6]研究了轴向加卸载条件下含水率对红砂岩能量演化的影响。Wang等[7]定量研究了能量对岩石损伤程度的影响，分析了岩石在循环加载和卸载过程中能量耗散和能量转换的规律。Bańka等[8]将数值模拟和能量耗散理论相结合，阐述了岩石破裂和弹性应变能之间的关系。

近年来，还有一些学者对岩石能量耗散和破碎特征之间的关系进行了探索。王利等[9]结合能量守恒关系以及分形理论，建立了岩石损伤能量碎块尺寸关系，研究成果在岩石块度分布预测中具有重要的工程应用价值。张蓉蓉等[10]通过分离式霍普金森压杆试验，研究了高低温处理后砂岩破碎分形维数和能量耗散之间的关系，认为相同温度下两者之间呈线性正相关关系。Peng等[11]对600 m深的煤岩进行了三轴压缩试验，提出了一个新的破坏能量比指标用以描述煤岩的破坏模式，并发现破坏能量比与破坏后碎屑的分形维数具有线性关系，破坏能量比越高，分形维数越大。Deng等[12]对花岗岩和砂岩在5种不同的冲击速度下进行了动态单轴压缩试验，通过筛分试验获得了碎屑的尺度分布，并建立了岩石破碎过程能量耗散模型。

上述研究主要针对完整岩石，但是工程岩体中常孕育着不同尺度、特性的地质结构面，不仅控制着岩体的变形破裂行为，而且对能量耗散和释放规律也有一定的影响。因此，笔者在不同裂隙倾角砂岩试件单轴压缩试验研究的基础上，分析了裂隙砂岩变形破裂过程中的能量演化特征，引入分形理论定量表征了破坏后碎屑尺度分布的分形特征，初步探究了裂隙砂岩耗散应变能、抗压强度以及分形维数之间的相关性，从能量的角度揭示岩石破坏过程中应力释放和耗散的规律，对阐明岩石的破坏机理提供参考。

1 试件制备及试验方案

1.1 试件制备

本次试验选取红砂岩作为研究对象，岩样取自云南省楚雄彝族自治州，表面光滑平整，呈致密块状构造。为了避免岩石各向异性的影响，选用同一块红砂岩板进行切割，并打磨成尺寸为120 mm×60 mm×25 mm（长×宽×厚）的长方体，如图1所示。采用高速水刀切割技术加工长度为2l=26 mm的预制裂隙，裂隙中点与试件中心点重合，裂隙分布如图1所示。裂隙倾角β分别设置为15°、30°、45°、60°和75°共5种情况，每种裂隙倾角制备2个试样。在预制裂隙中插入云母片，用于模拟闭合型裂隙。制备好的裂隙砂岩试件如图2所示。

1.2 试验装置及实验方案

单轴压缩试验加载设备采用WAW1000型电液伺服万能材料试验机，具有刚度大、稳定性好以及测量精度高等特点。试验开始前，将砂岩试件放置于试验机上，在试件上下端面加设刚性垫片，以减小加载过程中的摩擦效应。本次试验采用位移加载控制，加载速率设置为0.3 mm/min。试验机配套软件自动记录试验过程中的轴向载荷和位移数据。采用高清摄像机记录裂纹萌生、扩展和贯通的全过程，摄像机放置于距离试件正面1 m处。试验研究发现5种裂隙倾角试件的破坏模式基本一致，都表现为沿裂隙面发生剪切破坏。

2 能量耗散特征

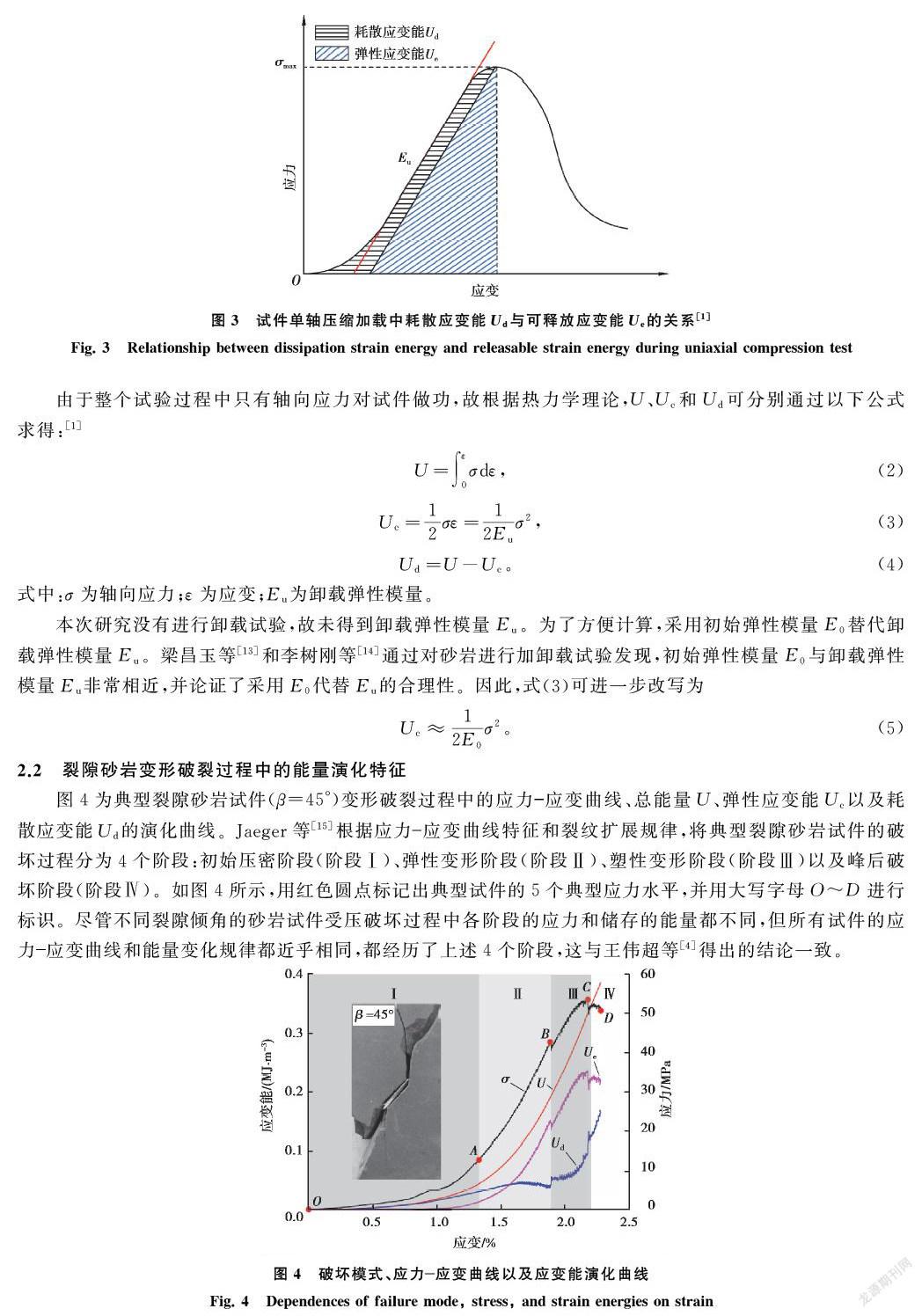
能量耗散和释放在岩石的变形破坏中起着重要的作用。从能量转化的意义上讲，岩石的破坏，包括裂隙的萌生、扩展和贯通，本质上是一个热力学过程，伴随着能量的耗散和释放。能量耗散导致岩石内部发生劣化，能量释放导致岩石结构突变，而当应变能急剧释放，岩石将发生破坏，在某些特定条件下，这是造成重大地质灾害的因素之一。因此，有必要对变形和破坏过程中岩石的能量耗散和释放规律进行研究。

2.1 应变能计算方法

假定单轴压缩试验环境与外界不存在热交换效应，忽略岩块弹射而转化的动能，则外力所做功（试验机对试件做的功）的总输入能量U即为总应变能，根据热力学第一定律可以得到单轴压缩过程中应变能的计算公式[1]

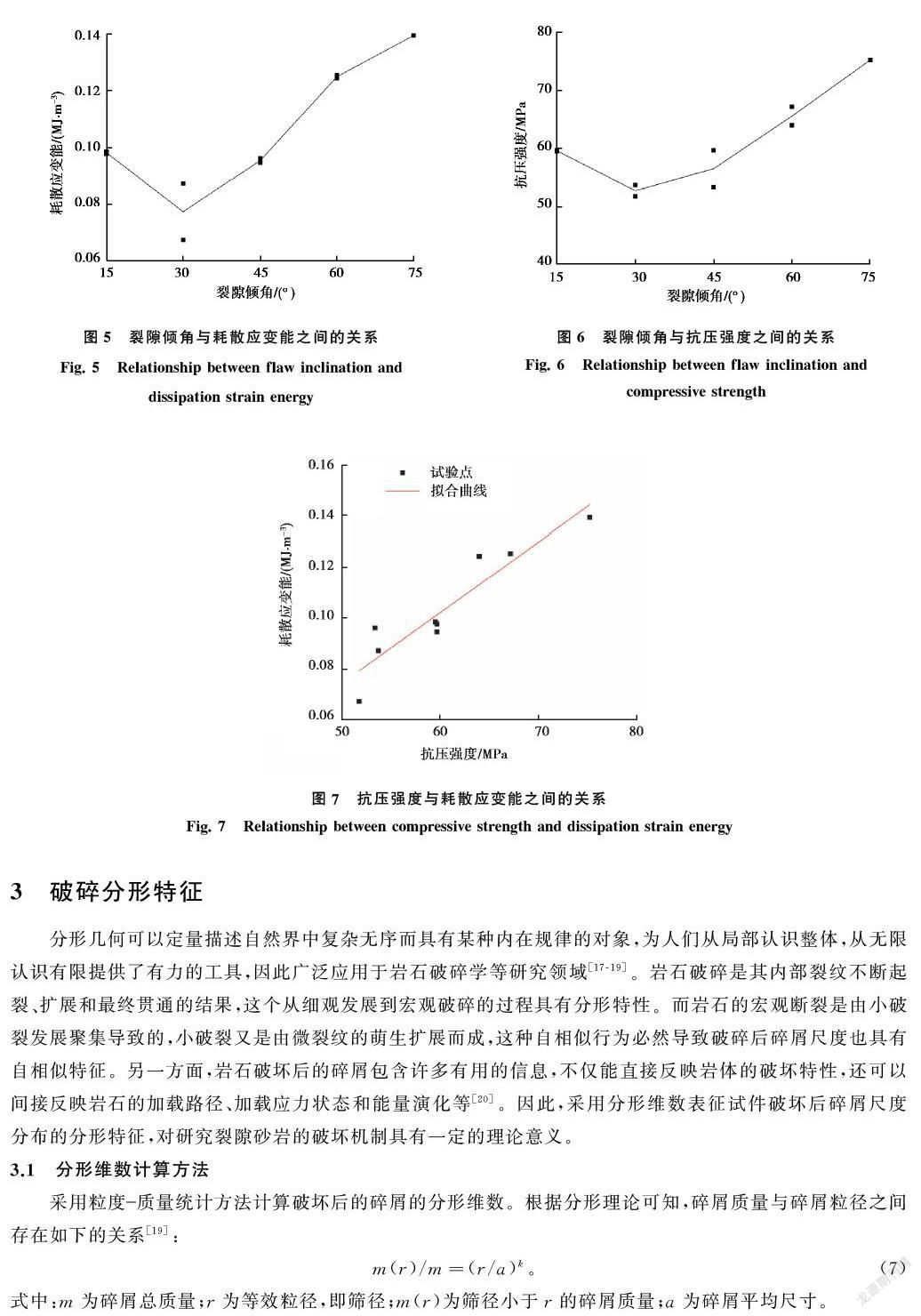
初始压密阶段（阶段Ⅰ）：试件内部的原生微裂隙在外力作用下逐渐闭合，应力应变曲线OA段呈下凹型。外力对试件做功，岩石逐渐积聚能量，而由于应力较小，总应变能、弹性应变能以及耗散应变能的增加速率较小，呈非线性上升趋势。在这个阶段，岩石吸收的部分能量转化为耗散应变能，这说明初始压密阶段，试件内部的微裂隙的闭合和摩擦滑移等行为消耗了一定的能量，尤其是预制裂隙的影响较大。

弹性变形阶段（阶段Ⅱ）：应力应变曲线AB段近似呈线性变化。随着轴向应力不断增大，岩石试件存储的能量不断增加，其增长速率远大于阶段Ⅰ。由于原生裂隙和预制裂隙多数被压密闭合，试件在这个阶段又不断地发生弹性变形，因此试件吸收的应变能绝大部分是弹性应变能，只有少量的能量耗散，耗散应变能曲线甚至有小量下降的趋势。

塑性变形阶段（阶段Ⅲ）：在较高的应力作用下，试件仍不断吸收能量，总能量曲线依旧呈上升趋势。翼裂纹开始从预制裂隙尖端起裂，在应力应变曲线中可以观察到明显的应力下跌（B点），弹性应变能曲线发生突降，而耗散应变能曲线出现突升。岩石内部微缺陷不断扩展、贯通，损伤量不断增大，导致耗散应变能呈加速增长趋势，耗散应变能的占比也逐渐升高。当应力达到峰值（C点）时，观察到宏观剪切裂纹的萌生，此时应力、弹性应变能和耗散应变能出现更大幅度的突变。

峰后破壞阶段（阶段Ⅳ）：应力达到峰值后，裂纹的快速扩展和贯通导致试件失去承载力并发生破坏。在应力下跌过程中（C点到D点），弹性应变能曲线逐渐下降，而耗散应变能曲线快速上升。峰值点以前，外力对试件做的功被试件的自身变形转化为弹性应变能，少部分能量被试件损伤扩展消耗掉。随着砂岩试件损伤逐步累积，试件慢慢发生劣化，耗散应变能也不断增大，达到一定程度后导致试件强度丧失。当应力达到峰值强度后，大量弹性应变能急剧释放，其中一些能量转化为其他形式的能量耗散掉，其形式包括裂纹扩展所需的表面能、微裂隙间相互摩擦的摩擦热能和振动弹射碎片的机械能等。弹性应变能释放量越多，释放速率越快，试件张性破坏特性越明显，裂隙砂岩试件被破碎成更小的碎片，导致更严重的破坏。

2.3 能量耗散与抗压强度之间的关系

峰值应力点是裂隙砂岩试件强度丧失至整体失稳破坏的临界点。裂隙砂岩在达到峰值强度之前，总应变能U和弹性应变能Ue逐渐增加;而耗散应变能Ud随着应力的增大经历了由缓慢增长到突然增长的变化过程。在一定荷载水平下，由于其微裂纹扩展、贯通以及破裂面摩擦错动，使岩石的黏聚力减小，耗散应变能增加。达到峰值强度后，弹性应变能急剧释放使裂纹的不稳定扩展和贯通加剧，导致试件破裂面扩大直至岩石失稳破坏。

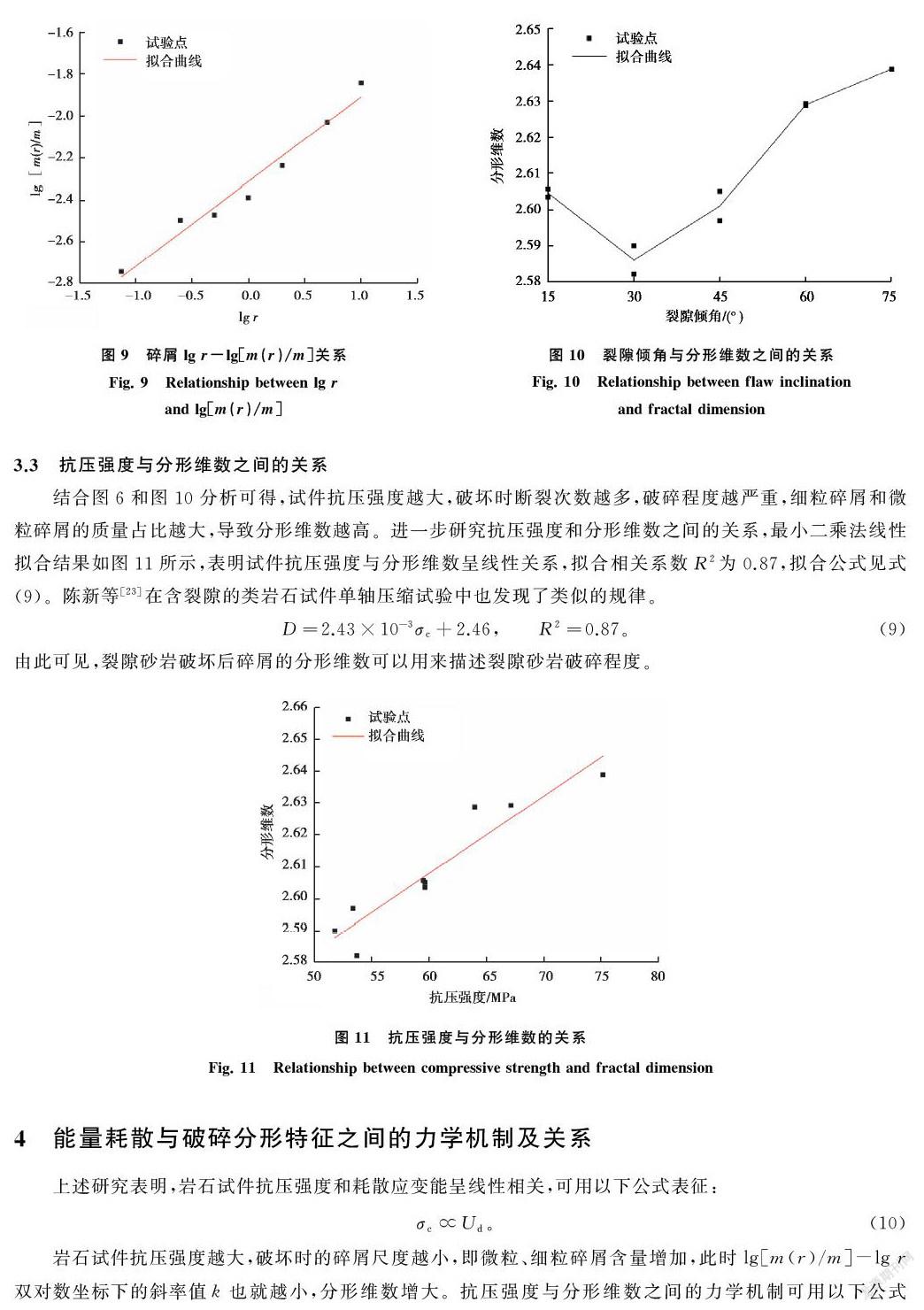
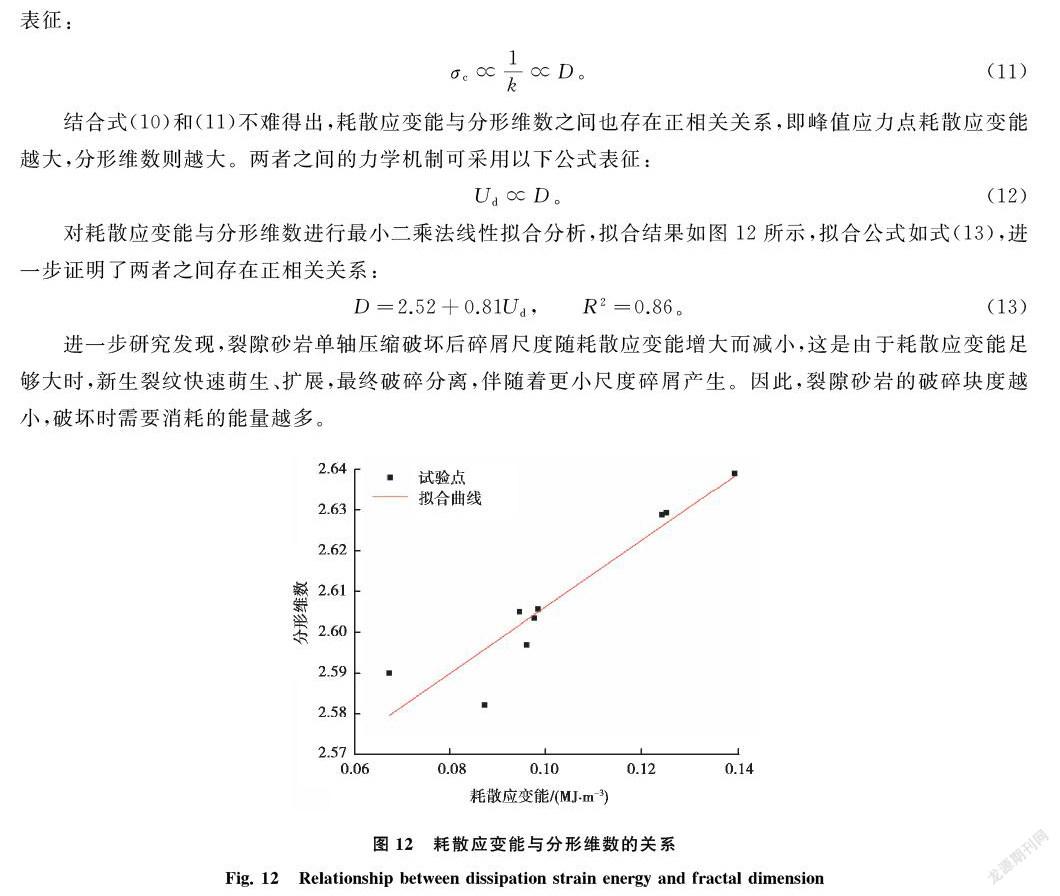
裂隙倾角与峰值应力点耗散应变能之间的关系如图5所示。图6为试件裂隙倾角与抗压强度之间的关系。需要指出的是，当裂隙倾角β = 75°时，只有1个试件的试验结果有效，这是因为该组其余试件表面均存在明显缺陷。随着裂隙倾角增大，试件峰值应力点耗散应变能和抗压强度均呈现出先减小后增大的变化规律。当裂隙倾角β = 30°时，试件抗压强度和耗散应变能均为最小值。结合图5和6可知，试件峰值应力点耗散应变能和抗压强度之间可能存在正相关关系。为此，采用最小二乘法对峰值应力点耗散应变能和抗压强度进行线性拟合，结果如图7所示，峰值应力点耗散应变能和抗压强度间近似呈线性相关，相关系数R2为0.87，拟合公式见式（6）。左建平等[16]研究发现煤岩峰前积蓄的能量与单轴抗压强度大致呈正比关系。

Ud=2.77×10-3σc-6.41×10-2，  R2=0.87。（6）

耗散应变能的演化使裂隙砂岩的强度发生劣化，最终导致结构破坏。试件抗压强度越高，破坏前积聚的可释放弹性应变能越多，破坏时转化成的耗散应变能越多，损伤程度越高。换句话说，能量耗散与裂隙砂岩的损伤以及强度劣化直接相关。

3 破碎分形特征

分形几何可以定量描述自然界中复杂无序而具有某种内在规律的对象，为人们从局部认识整体，从无限认识有限提供了有力的工具，因此广泛应用于岩石破碎学等研究领域[17-19]。岩石破碎是其内部裂纹不断起裂、扩展和最终贯通的结果，这个从细观发展到宏观破碎的过程具有分形特性。而岩石的宏观断裂是由小破裂发展聚集导致的，小破裂又是由微裂纹的萌生扩展而成，这种自相似行为必然导致破碎后碎屑尺度也具有自相似特征。另一方面，岩石破坏后的碎屑包含许多有用的信息，不仅能直接反映岩体的破坏特性，还可以间接反映岩石的加载路径、加载应力状态和能量演化等[20]。因此，采用分形维数表征试件破坏后碎屑尺度分布的分形特征，对研究裂隙砂岩的破坏机制具有一定的理论意义。

3.1 分形维数计算方法

采用粒度质量统计方法计算破坏后的碎屑的分形维数。根据分形理论可知，碎屑质量与碎屑粒径之间存在如下的关系[19]：

从图10中还发现分形维数与裂隙倾角密切相关，随着裂隙倾角增大，分形维数表现出先减小后增大的变化规律;当裂隙倾角β = 30°时，分形维数最小，这与抗压强度的变化规律相似。

3.3 抗压强度与分形维数之间的关系

结合图6和图10分析可得，试件抗压强度越大，破坏时断裂次数越多，破碎程度越严重，细粒碎屑和微粒碎屑的质量占比越大，导致分形维数越高。进一步研究抗压强度和分形维数之间的关系，最小二乘法线性拟合结果如图11所示，表明试件抗压强度与分形维数呈线性关系，拟合相关系数R2为0.87，拟合公式见式（9）。陈新等[23]在含裂隙的类岩石试件单轴压缩试验中也发现了类似的规律。

D=2.43×10-3σc+2.46，  R2=0.87。（9）

由此可见，裂隙砂岩破坏后碎屑的分形维数可以用来描述裂隙砂岩破碎程度。

需要说明的是，岩石是一种有着复杂内部结构的地质体[24]，不可避免地导致本次试验数据具有离散性，但抗压强度、耗散应变能和分形维数三者两两之间仍表现出明显的总体规律，如图7、11和12所示，相应的拟合相关系数R2均大于0.86。在今后的研究工作中，将增加试件数量，进一步验证和完善本文中提出的研究结论。

5 结 论

从能量角度出发，研究了含不同裂隙倾角的砂岩试件在单轴压缩作用下的能量耗散、力学特性以及破坏后的碎屑尺度分布特征，讨论了三者之间的关系，得出了以下结论。

1）不同裂隙倾角的岩体应变能演化过程大致相同，都经历了初始压密阶段、弹性变形阶段、塑性变形阶段以及峰后破坏阶段。

2）裂隙砂岩试件的抗压强度和峰值应力点耗散应变能表现出相似的变化规律。随着裂隙倾角增大，两者均表现为先减小后增大的趋势。当裂隙倾角β = 30°时，耗散应变能和抗压强度都最小。数据拟合结果表明，抗压强度和峰值应力点耗散应变能近似呈正相关关系。

3）筛分试验发现试件受压破坏后的碎屑尺度分布具有分形特征，计算所得的分形维数介于2.58～2.64之间，大于完整岩石的分形维数。随着裂隙倾角增大，分形维数表现为先减小后增大的变化规律，与抗压强度的变化规律类似。试件抗压强度与碎屑尺度分布分形维数近似呈正相关关系。

4）能量耗散与破碎分形特征之间关系的研究结果表明，裂隙岩体能量耗散与破碎分形特征之間具有较好的相关性。这是因为岩体抗压强度越高，表明抵抗外力破坏的能力越强，所需的耗散应变能也就越大，导致试件破碎程度越高，相应的分形维数随之增大。

参考文献：

[1] Xie H P， Li L Y， Peng R D， et al. Energy analysis and criteria for structural failure of rocks[J]. Journal of Rock Mechanics and Geotechnical Engineering， 2009， 1（1）： 11-20.

[2] Xie H P， Li L Y， Ju Y， et al. Energy analysis for damage and catastrophic failure of rocks[J]. Science China Technological Sciences， 2011， 54（S1）： 199-209.

[3] 孟庆彬， 韩立军， 浦海， 等. 应变速率和尺寸效应对岩石能量积聚与耗散影响的试验[J]. 煤炭学报， 2015， 40（10）： 2386-2398.

Meng Q B， Han L J， Pu H， et al. Experimental on the effect of strain rate and size on the energy accumulation and dissipation of rock[J]. Journal of China Coal Society， 2015， 40（10）： 2386-2398.（in Chinese）

[4] 王伟超， 刘希亮， 王利， 等. 预制裂纹盐岩单轴力学特性及能量机制试验[J]. 重庆大学学报， 2016， 39（5）： 103-113.

Wang W C， Liu X L， Wang L， et al. Mechanical behavior and energy mechanism of salt rock with prefab fissures under uniaxial compression[J]. Journal of Chongqing University， 2016， 39（5）： 103-113.（in Chinese）

[5] Chen Y， Guo B H. Crack closure effect and energy dissipation model for rocks under uniaxial compression[J]. Geotechnical and Geological Engineering， 2020， 38（1）： 621-629.

[6] Zhang Z Z， Gao F. Experimental investigation on the energy evolution of dry and water-saturated red sandstones[J]. International Journal of Mining Science and Technology， 2015， 25（3）： 383-388.

[7] Wang C L， He B B， Hou X L， et al. Stress-energy mechanism for rock failure evolution based on damage mechanics in hard rock[J]. Rock Mechanics and Rock Engineering， 2020， 53： 1021-1037.

[8] Bańka P， Chmiela A， Menéndez Fernández M， et al. Predicting changes in induced seismicity on the basis of estimated rock mass energy states[J]. International Journal of Rock Mechanics and Mining Sciences， 2017， 95： 79-86.

[9] 王利， 高謙. 基于损伤能量耗散的岩体块度分布预测[J]. 岩石力学与工程学报， 2007， 26（6）： 1202-1211.

Wang L， Gao Q. Fragmentation distribution prediction of rock based on damage energy dissipation[J]. Chinese Journal of Rock Mechanics and Engineering， 2007， 26（6）： 1202-1211. （in Chinese）

[10] 张蓉蓉， 经来旺. SHPB试验中高低温作用后深部砂岩破碎程度与能量耗散关系分析[J]. 煤炭学报， 2018， 43（7）： 1884-1892.

Zhang R R， Jing L W. Analysis on the fragment and energy dissipation of deep sandstone after high/low temperature treatment in SHPB tests[J]. Journal of China Coal Society， 2018， 43（7）： 1884-1892. （in Chinese）

[11] Peng R D， Ju Y， Wang J G， et al. Energy dissipation and release during coal failure under conventional triaxial compression[J]. Rock Mechanics and Rock Engineering， 2015， 48（2）： 509-526.

[12] Deng Y， Chen M， Jin Y， et al. Theoretical analysis and experimental research on the energy dissipation of rock crushing based on fractal theory[J]. Journal of Natural Gas Science and Engineering， 2016， 33： 231-239.

[13] 梁昌玉， 李晓， 王声星， 等. 岩石单轴压缩应力-应变特征的率相关性及能量机制试验研究[J]. 岩石力学与工程学报， 2012， 31（9）： 1830-1838.

Liang C Y， Li X， Wang S X， et al. Experimental investigations on rate-dependent stress-strain characteristics and energy mechanism of rock under uniaxial compression[J]. Chinese Journal of Rock Mechanics and Engineering， 2012， 31（9）： 1830-1838. （in Chinese）

[14] 李树刚， 陈高峰， 双海清， 等. 加载速率和初始损伤对砂岩能量演化影响的试验研究[J]. 采矿与安全工程学报， 2019， 36（2）： 373-380.

Li S G， Chen G F， Shuang H Q， et al. Experimental study on effect of loading rate and initial damage on energy evolution of sandstone[J]. Journal of Mining & Safety Engineering， 2019， 36（2）： 373-380. （in Chinese）

[15] Jaeger J C， Cook N G W， Zimmerman R W. Fundamentals of rock mechanics[M]. 4th ed. Blackwell， Oxford： Wiley， 2007.

[16] 左建平， 陈岩， 崔凡. 不同煤岩组合体力学特性差异及冲击倾向性分析[J]. 中国矿业大学学报， 2018， 47（1）： 81-87.

Zuo J P， Chen Y， Cui F. Investigation on mechanical properties and rock burst tendency of different coal-rock combined bodies[J]. Journal of China University of Mining & Technology， 2018， 47（1）： 81-87.（in Chinese）

[17] Zhang K， Chen Y L， Fan W C， et al. Influence of intermittent artificial crack density on shear fracturing and fractal behavior of rock bridges： experimental and numerical studies[J]. Rock Mechanics and Rock Engineering， 2020， 53（2）： 553-568.

[18] Mahdevari S， Moarefvand P. Experimental investigation of fractal dimension effect on deformation modulus of an artificial bimrock[J]. Bulletin of Engineering Geology and the Environment， 2018， 77（4）： 1729-1737.

[19] 谢和平. 分形岩石力学导论[M]. 北京： 科学出版社， 2005： 228-234.

Xie H P. Fractal-rock mechanics induction[M]. Beijing： Science Press， 2005： 228-234. （in Chinese）

[20] 黄达， 谭清， 黄润秋. 高围压卸荷条件下大理岩破碎块度分形特征及其与能量相关性研究[J]. 岩石力学与工程学报， 2012， 31（7）： 1379-1389.

Huang a， Tan Q， Huang R Q. Fractal characteristics of fragmentation and correlation with energy of marble under unloading with high confining pressure[J]. Chinese Journal of Rock Mechanics and Engineering， 2012， 31（7）： 1379-1389.（in Chinese）

[21] 姚璐， 张学民， 余涛. 中国区域电离层TEC与月均值偏差的空间相关性研究[J]. 地球物理学报， 2014， 57（11）： 3600-3610.

Yao L， Zhang X M， Yu T. A study of spacial correlation of monthly mean deviation of ionospheric TEC over China[J]. Chinese Journal of Geophysics， 2014， 57（11）： 3600-3610. （in Chinese）

[22] 高峰， 谢和平， 赵鹏. 岩石块度分布的分形性质及细观结构效应[J]. 巖石力学与工程学报， 1994， 13（3）： 240-246.

Gao F， Xie H P， Zhao P. Fractal properties of size frequency distribution of rock fragments and the influence of meso-structure[J]. Chinese Journal of Rock Mechanics and Engineering， 1994， 13（3）： 240-246. （in Chinese）

[23] 陈新， 王仕志， 李磊. 节理岩体模型单轴压缩破碎规律研究[J]. 岩石力学与工程学报， 2012， 31（5）： 898-907.

Chen X， Wang S Z， Li L. Characteristics of fragments of jointed rock mass model under uniaxial compression[J]. Chinese Journal of Rock Mechanics and Engineering， 2012， 31（5）： 898-907.（in Chinese）

[24] 钟志彬， Hu X Z， 邓荣贵， 等. 含裂隙充填节理岩体的压剪断裂机制研究[J]. 岩石力学与工程学报， 2018， 37（S1）： 3320-3331.

Zhong Z B， Hu X Z， Deng R G， et al. Study on the compression-shear fracture mechanism of infilled jointed rock mass with pre-crack[J]. Chinese Journal of Rock Mechanics and Engineering， 2018， 37（S1）： 3320-3331.（in Chinese）

（编辑 罗 敏）