基于BP神经网络的基坑沉降量的预测研究
吴佳俊,刘保民,刘念
(河南理工大学 资源环境学院,河南 焦作,454000)
近年来,随着城市化和经济的快速发展,我国高层建筑和城市地铁站数量日益增长,这些建筑大都涉及基坑工程,基坑开挖深度通常为10 m左右,有的深基坑也有着几十米的深度[1]。由于深基坑的工程地质条件、施工条件等非常复杂,在施工过程中容易引起基坑稳定性变化,这些安全问题受到业界的广泛关注[2]。目前,深基坑开挖与支护的预测理论和技术方面还不够成熟,仅仅依靠现有的理论和实证分析,不足以保证基坑开挖后的稳定性。因此,施工现场的监测、变形控制和沉降预测对深基坑的施工非常重要[3]。
1 BP神经网络原理
1.1 神经网络简介
人工神经网络是模仿动物神经网络行为特征的模型。BP神经网络的学习过程可以分为两部分:信号的正向传播和误差的反向传播,在正向传播过程中,信号作用于输入层,经过隐藏层处理后到达输出层,输出层输出结果信号[4-5],见图1。如果输出结果与预期输出的结果不匹配,则输入错误反转。同时,将错误分配给该层的所有单元,并校正这些单元的权重。该过程一直循环直到输出层的误差小于设置值或达到预设的学习时间[5]。
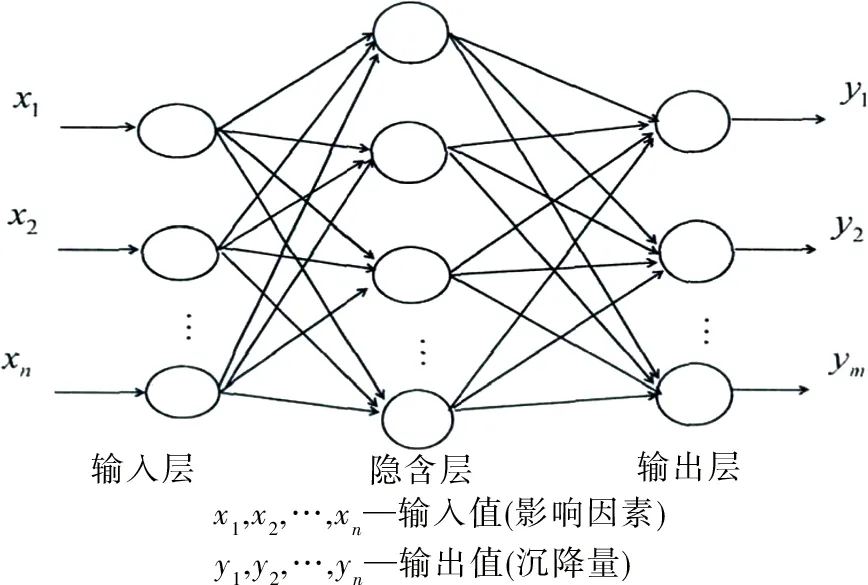
图1 BP神经网络Fig.1 BP neural network
1.2 神经网络应用的基本条件
1)隐藏层的节点数目要小于进入训练的样本的总体数量。
2)连接权重的数量要小于进入训练的样本的总体数量。
3)只有多次进行训练,多次赋值权重,才可能在全局最小点附近获得可行的解决方案。
1.3 适用性分析
运用BP神经网络对基坑沉降量进行预测具有如下优点:
1)非线性映射能力。运用BP神经网络可以进行非线性映射运算。基坑沉降受许多因素影响,这些因素间具有一定的关系,而神经网络学习可以较好地处理这些关系。
2)泛化能力。即使网络学习中没有相关的样本数据,神经网络也能在输入和输出这个过程中找到正确的映射。
3)客观性。神经网络只需要在学习过程输入学习样本,对学习样本进行训练,这更加具有客观性和说服力[5-6]。
1.4 BP神经网络具体流程
BP神经网络的训练一般分为如下7步:
1)初始化BP神经网络。归一化处理,将各个数据赋值为[-1,1]之间的数。设置误差函数erfx,允许精度eps和最多学习次数L。
2)选取xk(1≤k≤Y)随机样本进行学习,设定这个样本的期望输出为dk。
3)计算隐含节点j(1≤j≤p)的输入netj,则其输出层输出为
(1)
4)运用神经网络期望输出值和实际输出值,计算误差函数对各个神经元的偏导数δ0(k)。
5)修正各个网络之间的连接权值。
6)计算网络输出误差函数:
(2)
式中:dqk为输出期望值;zqk为实际输出值。
7)判别erfxq和eps的关系。当erfxq
2 基坑沉降量预测
2.1 神经网络模型设计
在BP神经网络首席训练时,需要对神经网络的允许精度eps和最大学习次数以及隐含层节点数x进行设定。本文设定eps=10-3,L=50 000,x为1。
张德富等[7]通过苏州23座车站基坑监测数据分析当地基坑变形特性,并分析土体重度、开挖深度对基坑变形的影响。刘超等[8]在研究变形预测系统时发现基坑内支撑数量以及土体内摩擦角对基坑沉降量有影响。总结出影响基坑沉降量的主要因素有6个:土体重度、内摩擦角、内聚力、开挖深度、内部支撑的数量和距基坑的距离。因此,神经网络的输入层选取以上6个主要影响因素。网络的输出层中有1个元素,即预测的结算值。这样,输入层有6个神经元,输出层有1个神经元,中间层的神经元数量可以采用不同的值尝试,而误差最小的是最终结果[9]。
数据归一化处理指的是把目标内所有数据转化为[-1,1]之间的数,取消了各数据间的数量级差别,避免输入、输出时这种数量级差别较大,方便进行后面的数据处理,同时保证程序运行时的收敛速度,转换函数如下:
(3)
其中,xmax表示样本数据的最大值;xmin表示样本数据的最小值。
对数据进行归一化处理之后,初始化BP神经网络时要根据系统输入、输出序列(X,Y)来确定输入层节点数量m,隐含层节点数量k,输出层节点数量w,学习速率λ,目标误差α,迭代次数量β。预测模型的6个输入层变量与输出层沉降量呈非线性函数关系,由此建立6-Nt-1结构的神经网络,其中,Nt为第t层隐含层节点数量k的值。
据此,隐含层传输函数采用tansig函数:
(4)
输出层传输函数采用purelin函数:
a=n
隐含层神经元的个数对BP神经预测精度会产生较大影响,节点数量过少,网络不能很好学习,这样就需要增加训练次数,训练的精度也会受影响;节点的数量过多,网络训练时间会增加,也会受影响。参考式(5)来确定最佳隐含层神经元的个数。
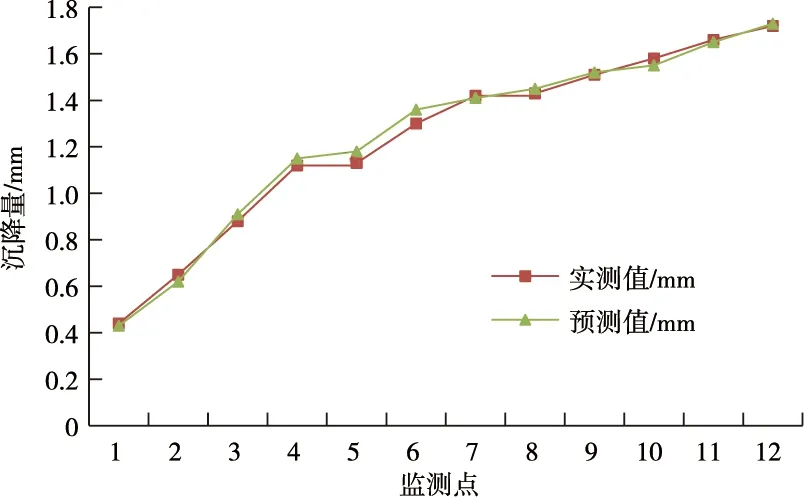
k (5) k=log2w 基坑的沉降过程受到很多因素的影响,不能仅依靠单个的理论分析来研究这个过程。神经网络是1个模糊的灰色计算过程,可以用来进行基坑沉降量的预测。本文运用MATLAB软件建立BP神经网络模型对某基坑沉降量进行预测,采用土体重度、内摩擦角、黏聚力、开挖深度、内支撑个数以及距基坑的距离6个指标,建立神经网络模型,预测基坑沉降情况[10]。运用MATLAB进行BP神经网络预测沉降量时,选取1个隐含层就能达到相应的预测精度[11]。 选取某深基坑工程现场20个监测点的实测数据,前12个作为神经网络训练样本,进行多次训练得到BP神经网络预测误差图,见图2。再对后8个监测点的沉降量进行预测对比分析,来验证BP神经网络在基坑沉降预测中的可靠性[12],见表1。 表1 学习测点样本数据 图2 BP神经网络预测误差图Fig.2 BP neural network prediction error map 从图2可以看出:训练得到的神经网络能较准确地反映土体重度、内摩擦角、黏聚力、开挖深度、内支撑个数以及距基坑的距离6个影响因素,与基坑沉降量之间有较高的相关性,据此,在MATLAB中模拟出基坑沉降量与土体重度、内摩擦角、黏聚力、开挖深度、内支撑个数以及距基坑的距离之间的关系[13-14],得到回归线性图,见图3。 图3 前12个监测点训练回归线性图Fig.3 Training regression linear chart of the first 12 monitoring points 从图3可知:目标输出与实际输出回归系数为0.999 12,说明训练的BP神经网络对该基坑沉降量预测的准确性非常高,有很高的可信度。 同时将前12个监测点基坑沉降量的预测值和实际值进行对比,更能直观地看出该预测方法的准确性,见图4。 图4 沉降量实测值与预测值的对比Fig.4 Linear graph of training regression for the first 12 monitoring points 从图4可以看出:基坑沉降的实测值和预测值之间存在较高重合性,说明BP神经网络对该基坑沉降量的预测可信度较高。由前12组样本的训练学习发现神经网络的准确性较高,对此,运用该网络对后8个监测点的沉降值进行预测,后8个监测点的实际沉降量和预测沉降量见表2。 表2 后8个监测点的实际沉降量和预测沉降量 从图5可以看出:后8个监测点沉降量的实测值和预测值也具有较高重合性,说明了BP神经网络的可靠性较高。 图5 后8个监测点沉降量实测值与预测值的对比Fig.5 Comparison of the measured and predicted settlements of the last 8 monitoring points 为了验证整个预测阶段的可靠性,将20个监测点的全部运用MATLAB进行训练得到它们的训练回归线性图,看它们的回归系数是否在可信区间内,回归线性图见图6。 图6 训练回归线性图Fig.6 Linear graph of training regression 通过对图6的分析,可以看出:整个目标输出与实际输出回归系数为0.997 85,在置信区间范围内,说明BP神经网络对该基坑沉降量预测的准确率非常高。 1)根据以往的实际工程案例分析以及相关资料,再结合某深基坑的现场地质条件和施工条件后,选择了土体重度、内摩擦角、内聚力、开挖深度、内支撑件数和距基坑的距离6项指标,建立了BP神经网络预测模型,对基坑沉降量进行预测。预测结果与实测值吻合性较好,预测值与实测值之间的误差基本控制在0.04 mm以内。 2)运用MATLAB语言编程,对基坑沉降量进行预测,操作简单,在前12组训练过程中,目标输出与实际输出回归系数为0.999 12,并且整个20组预测值和实际值的回归系数也达到了0.997 85。 3)对于许多基坑沉降、地基沉降等岩土工程问题,理论模型不能较好地解决这些问题。而BP神经网络具有良好的非线性映射能力,可以充分考虑各种因素之间的关系,对地面沉降量进行预测具有较高的可信度,可以用于后续的类似工程。2.2 沉降量预测






3 结论

