中小城市地铁运营与建设优化设计

程 栋，林靖和，张成基

(兰州工业学院 a.计算机与人工智能学院；b.电气工程学院；c.基础学科部，甘肃 兰州 730050)

地铁作为一种现代化的城市公交客运系统，具有运量大、速度快和节省城市空间等优点，其对城市的发展有着不可忽视的作用，已成为衡量城市经济发展的标志[1-4].但对于中小城市，地铁在给人们带来便利和快捷的同时也存在一定的困扰，主要表现为2方面：一是在人口密度小的城市，由于发车频次高但乘坐地铁的人数过少，导致地铁公司的运营效益呈亏损状态；二是在人口密集的城市，存在某个时间段乘坐地铁人数过多造成拥挤情况.因此，对于以上2个突出问题，建立合理运营模式与发车方案对于中小城市地铁的高效发展显得尤为重要.

1 地铁系统参数分析

地铁作为城市轨道交通系统，在评价时可作为参考指标的主要有客流量、客流的不均衡性、地铁的运营时间和行驶时间[5-7].本文主要从站席密度、地铁的影响范围与断面不均衡系数这3个参数的选择，来探讨如何缓解地铁公司亏损以及地铁站点内人员拥挤的问题.

1.1 站席密度

站席密度指在车厢的单位有效站立面积内平均站立的乘客人数，此参数反映了乘客乘坐地铁的舒适度.我国对站席密度的评判标准如表1所示.

表1 站席密度指标

断面客流量指在单位时间内通过地铁线路某一断面的客流量.若取地铁线路的每个站点作为断面，则根据地铁线路的单向最大断面客流量及车厢的站席面积可得到站席密度为

(1)

式中：ρ为车厢站席密度；pmax为线路单向最大断面客流量(人次)；sz为站席面积.

1.2 地铁线路影响范围

地铁线路的影响范围是指地铁线路所吸引客流的区域，也称为“吸引范围”，在该区域内，人们能够方便地直接或间接乘坐地铁[8].为了确定地铁线路与沿线常规公交线路之间的竞合关系，首先要分析地铁线路的影响范围，将其分为直接和间接影响范围.然后在不同影响范围内研究地铁与常规公交之间的竞争与合作.

本文以呼和浩特市的地铁线路为例，在地铁线路的直接影响范围内，乘客步行或骑单车至地铁站点乘坐地铁，这类客流一般分布在地铁站点附近.但由于该市共享单车投入量较少，加之骑自家单车去地铁站不方便停车，大部分人不会选择骑单车的方式，所以主要考虑乘客步行前往地铁站的方式.在地铁线路的间接影响范围内，乘客乘坐出租车、常规公交等其他交通方式来换乘地铁，由于该市的常规公交大部分处于地铁沿线位置，会在一定程度上扩大地铁站的影响范围.

基于该市地铁站的影响范围，假设人的步行速度平均为5 km/h，且到达地铁站的时间不超过10 min，则其直接影响范围半径最远可达833 m，加上沿线公交车对地铁站的间接影响，可扩大地铁站的影响范围半径为1 000 m.

1.3 单向断面不均衡系数

设研究断面为地铁线路的各站点，由单向最大断面客流量、断面的客流量、整条线路断面个数可计算得各个站点的不均衡系数为

(2)

式中：∂为线路单向面不均衡系数；pmax为线路单向最大断面客流量(人次)；pi为线路单向上第i个断面的客流量；k为整条线路断面个数.

如果∂≈1，表明该地铁线路单方向各个断面的客流量较均衡；∂≥1.5，表明客流量分布不均衡程度比较大.

2 模型建立与仿真

2.1 发车方案优化模型

呼和浩特市地铁主要采用B2车型[9]，车厢的长度为19 m，宽度为2.8 m，无司机车厢的坐席有46个，有司机车厢坐席有36个.1号线全程为21.7 km，共设站点20个；2号线全程27.3 km，共设站点24个，在每条地铁线路上均设有2台额定电压为110 kV的主变压器.

根据该市地铁运营数据[10]可知，地铁在相同的两站之间所耗时是一致的，且走完1号线全程耗时45 min，走完2号线全程耗时48 min.地铁的首班车6:00发出，末班车22:00发出，该城市工作日早高峰为7:00至9:00，晚高峰为17:00至19:00，低峰期为20:00至22:00，其余时间为平峰期；节假日及双休日早高峰为9:00至11:00，晚高峰为16:00至18:00，低峰期为20:00至22:00，其余时间为平峰期.2条地铁线路目前采取的发车方式为高峰期发车间隔6 min，平峰期发车间隔10 min，低峰期发车间隔12 min的方案.基于上述条件，从乘客体验与公司盈利2个角度出发，以站席密度为主要依据对发车方案进行优化.

根据呼和浩特市地铁官网，可查该市地铁收费标准如表2所示.

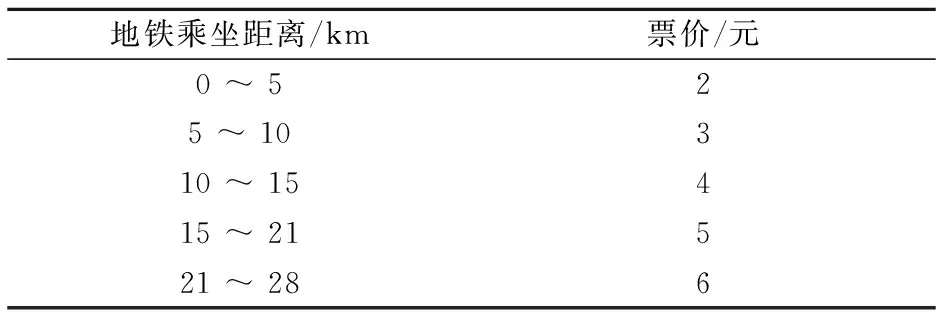
表2 呼和浩特市地铁收费标准

对于地铁公司而言，其主要经济来源为出售地铁票的收入，但统计乘客乘坐地铁距离的频次和站数有一定难度，所以无法具体得到地铁i号线乘客购票的人均票价mi，故采用以下方法对乘客购票的平均票价进行估计.

假设每条地铁线上每2个车站之间的间距相等，则可以分别计算出2条线路上相邻站点之间的距离.假设某乘客从任意站上车并从任意站下车，计算这2个站之间的距离，并按照标准收费，借助Python编程求出所有的可能性，并计算出所有可能性票价的平均值，以此值作为该乘客乘坐地铁所购买的票价.假设车站的通行人数为c，则可计算出呼和浩特地铁公司的收入Y为

Y=mi×c.

(3)

地铁公司的成本消费主要包括地铁运营所消耗的电费、工人工资及建设地铁站中必要建筑或设施的费用.当地铁每一次发车经过全程后所得收入大于每次发车耗电所损失的电费时，整个地铁公司才有可能减小亏损直到盈利，故只考虑地铁运营时所消耗的电费.地铁公司的电能主要是各站点用电设施的消耗及地铁运行的消耗，对于站点用电设施的消耗不再考虑，所以电量主要用于地铁发电机做功和车厢内部设施的消耗.

由于地铁在运行过程中会产生一定的再生电能，可为车厢内空调、照明灯等用电设备供电，所以忽略车厢内部用电设备的电能消耗.地铁发电机做功包括牵引力做功和克服重力做功，假设地铁全程都处于平地运行状态，只考虑牵引力做功所耗费的电量.呼和浩特市对于变压器额定电压在110 kV以下的工商业，收费标准为0.483 7元/(kw·h)；B2型列车每节车厢运行1 km消耗电能为3.41 kw·h[11].地铁在运行过程中全程匀速前进，忽略地铁进出站时因启停而消耗的电量，近似认为地铁牵引力做功全部由发电机做功提供.基于以上的表述和假设，确定地铁运行1次所消耗的成本为

X=0.483 7×3.41×l×q，

(4)

式中：l为线路长度；q为车厢数.

进一步可得公司总利润为

ω=Y-X.

(5)

2.2 地铁站选址优化模型与仿真

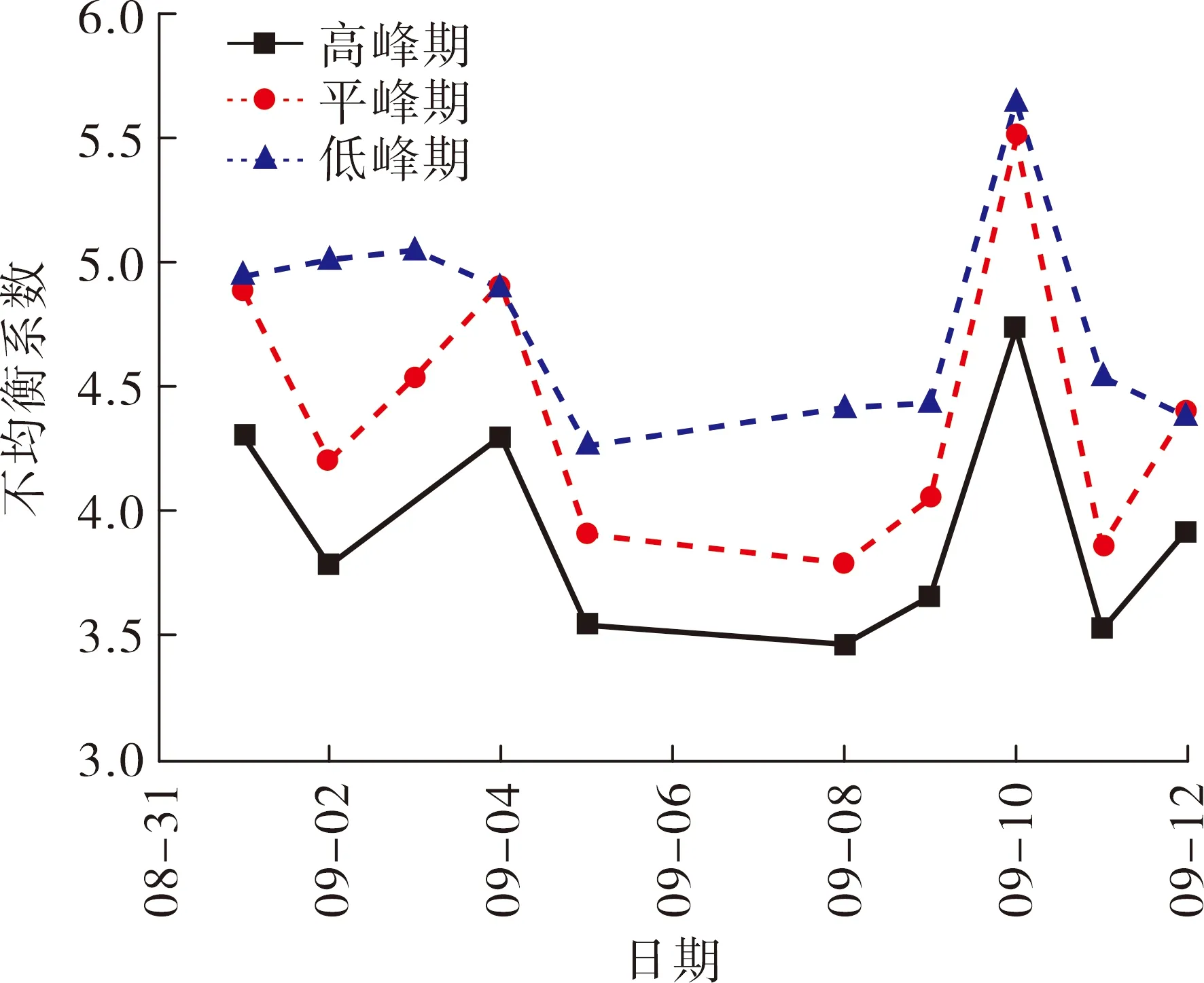
对于地铁站选址的优化，从地铁的影响范围与断面不均衡系数2个方面分析.首先根据文献[10]中给出的呼和浩特市2条地铁线运营相应数据，对各站的经纬度坐标利用MATLAB仿真(如图1所示)，并对地铁站点的影响范围进行分析；其次结合各站点的出入人数计算各时段的不均衡系数(以2号线为例，其2020年8～9月间曲线如图2～3所示)，通过对其分析可得出各站点的人流量分布.

图1 地铁行程线路

(a) 出站

图3 地铁选址优化线路

由图2可知：在高峰期、平峰期和低峰期，客流量在出入站的不均衡系数均在3.5以上，表明部分站点之间客流量悬差较大.因此，原发车方案可从站点分布密度与客流量大小角度改良，在后续的优化中还可以考虑加入不同的交路列车开行方案，以达到更好的经济性和客流匹配性.

将上述分析与地铁站的影响范围结合，在优化过程中，保持5个站点不变，即4个终点站和1个换乘站.根据原始每个站点的经纬度，借助Python计算每2个相邻站点之间的距离为

d=rarccos(cosy1cosy2cos(x1-x2)+siny1siny2)，

(6)

式中：r为地球半径，取r=6 370 m；xi为站点经度；yi为站点纬度.

利用上述计算方法可得到相邻2个站点之间的距离，并借助中点公式[12]求得2个站点的中点.根据相距距离的远近对2个站点进行调整，对于距离小于900 m的2个站进行分散处理，即将2个站点沿着其连线上远离中点的方向进行移动，直到2个站点的距离不小于900 m.对于距离大于1 100 m的2个站进行集中处理，即将2个站点沿着其连线上靠近中点的方向移动，直到2个站点的距离不大于1 100 m.如果2个站点中有一个属于保持不动的，则只对另一个站进行移动，最终将得到的新站点的经纬度坐标进行仿真.如图3所示为优化地铁选址线路图，图4是对优化前后地铁线路进行了对比.为了能够清楚地分辨优化前后线路的差别，对2条地铁线交叉位置进行了局部放大.

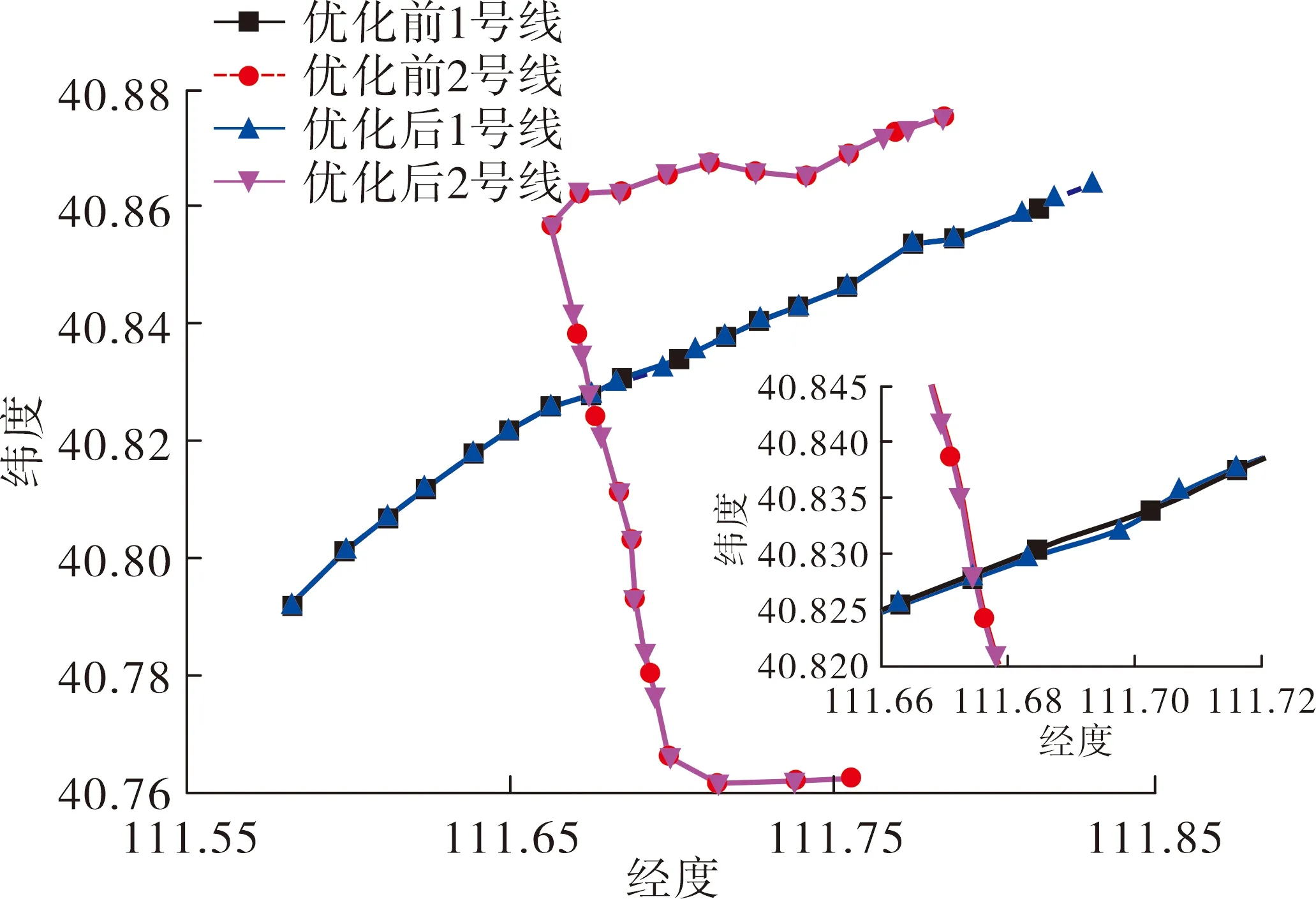
图4 地铁选址优化线路前后对比

以1号线为例，线路全长为21.7 km，设地铁站20个，共有19个间隔，则每2个车站之间的距离约为1.142 km，参照表2得出1～19个车站间隔的收费票价，如表3所示.

表3 地铁1号线优化模型收费标准

借助Python编程计算得到地铁1号线的人均票价m1为3.095元/人，地铁2号线的人均票价为m2为3.438元/人.通过对新选址方案模型分析，可得出在该优化模型情况下盈利时所需的人数.1号线按最优发车方案1天可发72趟次车，每趟消耗成本178.96元，人均票价为3.095元，预计1天载客4 163人次可盈利；2号线按最优发车方案1天可发72趟次车，每趟成本225.15元，人均票价为3.438元，预计1天载客4 715人次可盈利.

3 实例分析与优化

基于地铁发车方案模型进行分析，对工作日、双休日的1、2号线运行数据进行分类处理，以天为基准，借助Python编程算出每个站点的出入站人数，结合不同时段的发车频次得出总站席面积，最终算出所需站席密度.将不同车厢数和发车间隔对应的站席密度与相应指标比较，在考虑运营成本的基础上又使乘客舒适度不至于太低，从而得出一个择优方案的范围，再对其中方案进行成本对比，得出最优方案.

在计算站席密度时，假设每个坐席面积为0.1 m2，可得无司机车厢的坐席面积为18.4 m2，有司机车厢坐席面积为7.2 m2.由于车厢总面积为319.2 m2，从而可得到站席面积为293.6 m2.以入站高峰期为例得到站席密度如表4所示，其值远小于“非常舒适”水平的标准站席密度3.0(站席密度标准见表1)，说明地铁空位太多，资源浪费严重.本文将车厢数规定为3～5个，发车间隔高峰期规定至6～13 min，平峰期规定至6～15 min，低峰期规定至12～20 min.对应求出各出入站客流量的站席密度，结合“我国地铁乘客服务水平”与原发车方案的站席密度进行对比，得出3个车厢数不符合实际情况，故需在4个和5个车厢数中选择.

表4 高峰期地铁入站客流量站席密度 人/m2

高峰期地铁选择4个或5个车厢时都为间隔频次5 min或7 min；平峰期地铁选择4个车厢时间隔频次为9 min或10 min，5个车厢时间隔频次为7 min或8 min；低峰期地铁选择4个车厢时间隔频次为11 min，5个车厢时间隔频次为8 min或9 min.以入站高峰期站席密度为例，选择不同车厢时的站席密度，如表5所示.进而可得到不同情况下地铁运行1次所花费的成本，如表6所示.

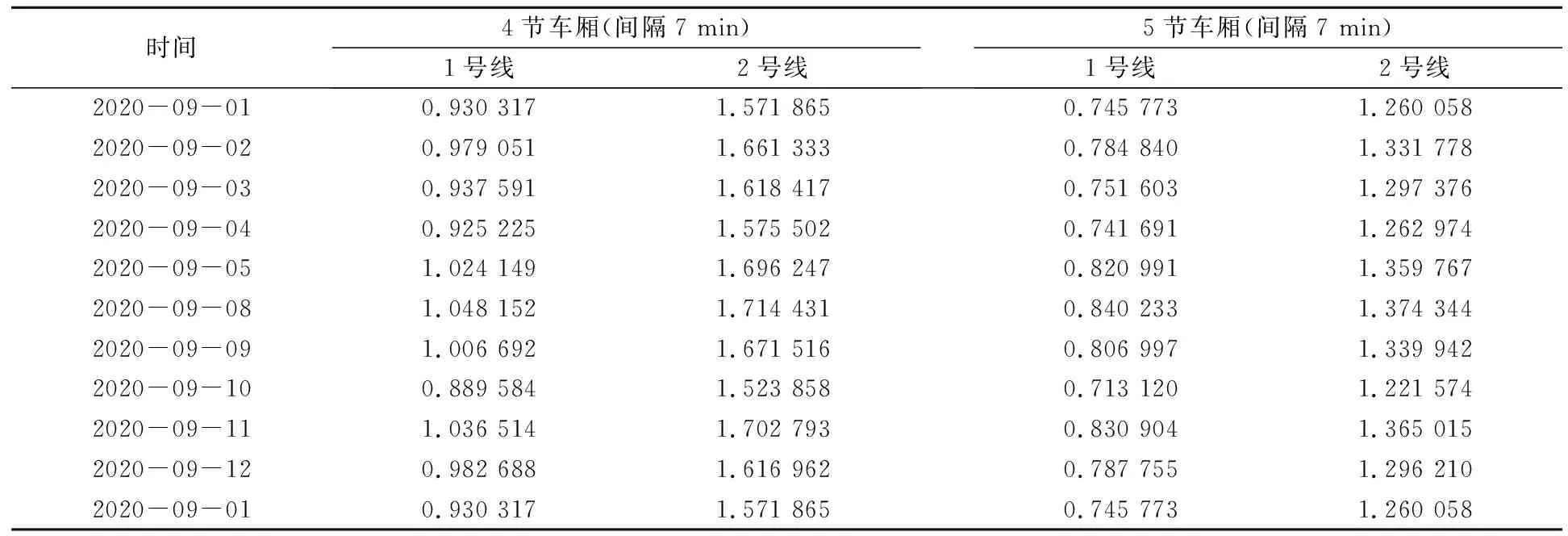
表5 入站高峰期选择不同车厢时的站席密度 人/m2

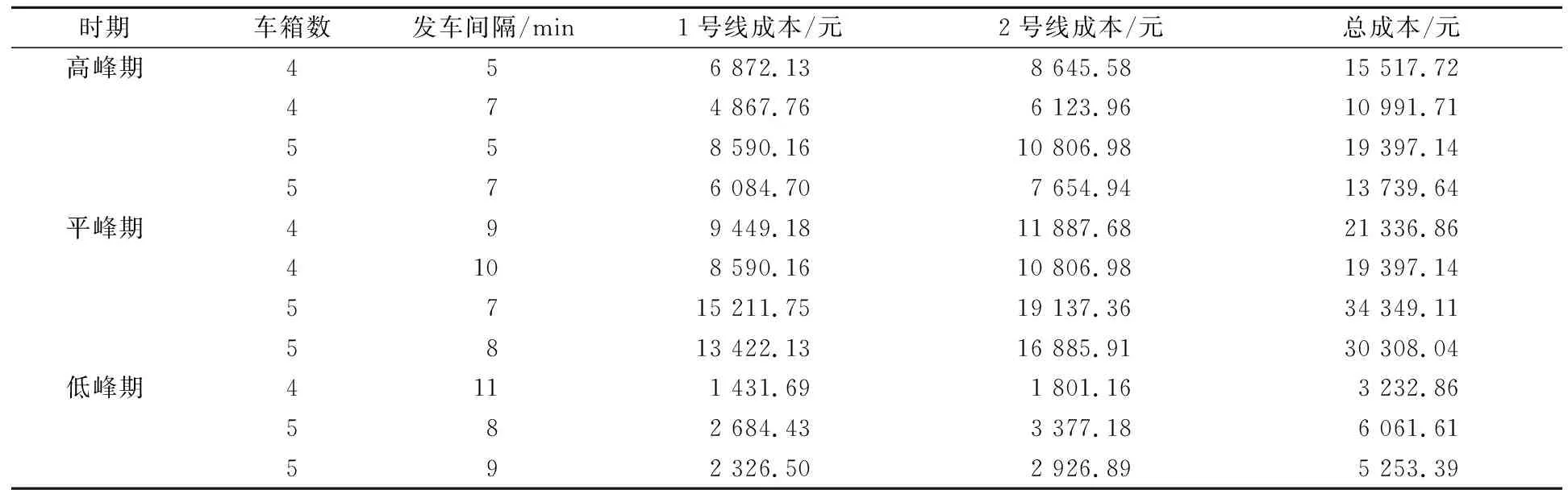
表6 各择优范围对应地铁花费成本

对比表5～6中的数据，从站席密度和总花费成本2个方面进行分析，运营成本较低且不浪费空间资源的情况优先选择，得出优化方案为：高峰期地铁选择4个车厢间隔频次7 min，平峰期地铁选择4个车厢间隔频次10 min，低峰期地铁选择4个车厢间隔频次11 min.

4 结语

本文主要以呼和浩特市地铁运行数据为基础，通过对站席密度、影响范围和断面不均衡系数进行分析、仿真和优化，得到了最优发车与选址的方案模型.该模型主要有2大优点：一是在地铁运营方面，总成本相对降低，客流分布相对均匀，盈利时最小乘车人次也相对减少；二是站席密度相对提高，乘客每次乘车时拥挤程度依然保持在“非常舒适”标准，有更好的体验感.本文得到的优化模型可为缓解部分中小城市的地铁公司运营亏损、地铁站人多拥挤等问题提供一定的理论支撑，为城市的绿色发展贡献绵薄之力.