智能小车的巡检引导线图像处理研究

戴 睿 ，谢 雁

1.中国航空研究院 研究生院，江苏 扬州 225006；2.沈阳飞机设计研究所 扬州协同创新研究院，江苏 扬州 225006

随着人工智能与传感器技术的发展，智能小车［1-5］越来越成为工业场景下的巡检工具。智能小车在执行巡检工作时，首先通过携带的摄像头采集周围环境的信息；再通过计算机视觉算法对采集到的图像信息进行识别与处理，确定图像中的障碍物与目标物；最后通过一系列控制算法，对小车的运动进行控制，使其完美地规避障碍物，从而顺利到达目标地点。

本文主要针对具有规则引导线的智能小车日常巡检中的直线导引和弧线导引进行研究。通过对采集到的图像信息进行识别，对目标场景的引导线进行阈值分割及边缘检测；再通过霍夫变换及骨架提取算法分别对直线引导线和弧线引导线进行追踪；最后通过参数化方法确定智能小车的设定点和设定方向。算法流程如图1所示。

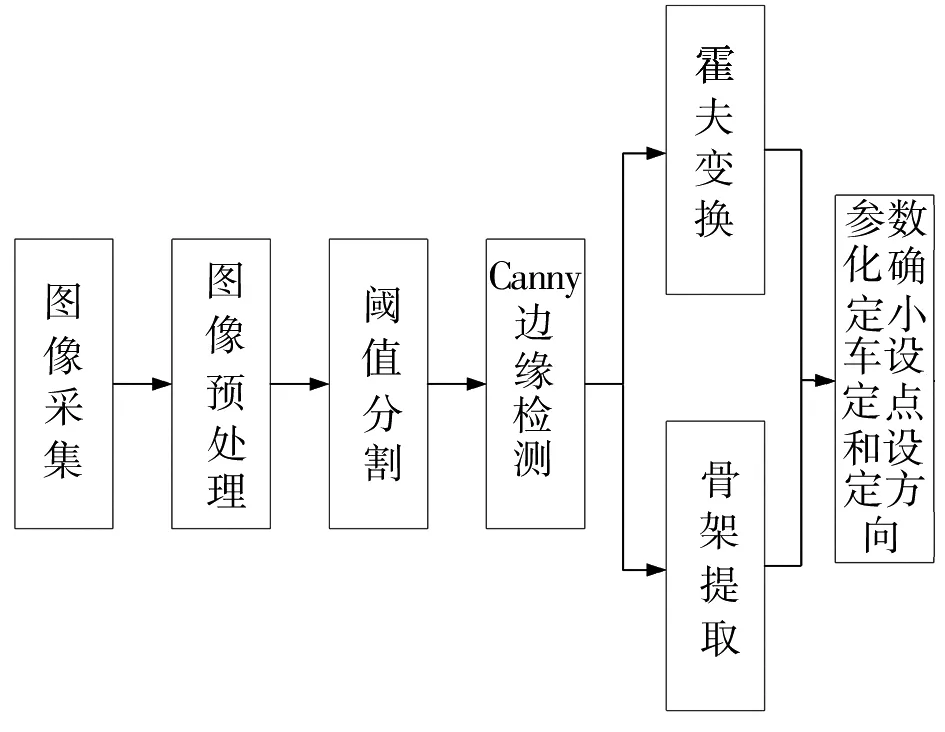
图1 行进道路路线确定流程Fig. 1 Road route determination process

1 图像预处理

根据图1 的算法流程，对于采集到的图像信息需要进行预处理，以减少图像识别中的无关信息，提高图像识别的鲁棒性。本文主要通过图像灰度化、尺寸调整、模式滤波［6］对采集到的图像进行预处理。由于智能小车在日常巡检中需要对目标场景的引导线进行阈值分割及边缘检测，而引导线的检测无需色彩信息，因此首先将原始输入图像进行灰度化处理；其次，为了提高算法的运行速度，需要对输入图像进行尺寸调整；最后，为了保留图像的边缘信息，滤除由于尺寸调整及原始输入所产生的噪音点，采用模式滤波器对调整过尺寸的图像进行滤波。经过图像预处理后，输出图像的像素计算如公式（1）所示。

式中：g(i，j)为输出图像像素点（i，j）的灰度值；f(k，l)为当前输入图像像素点（k，l）的灰度值；S(i，j) 是 以(i，j) 为 中 心 的 滤 波 核 所 在 区 间；w(i，j，k，l) =ws⋅wr（ws为基于空间的高斯函数，wr为基于像素的高斯函数），为由高斯函数经过两次计算得到的数值。

当引导线图像处于变化程度小的区域时，wr无限趋近于1，此时模式滤波为高斯滤波；当引导线图像处于变化程度高的区域时，wr与ws都无限趋近于0，此时可将图像输入。因此，通过模式滤波器能有效地保留引导线图像的边缘信息。

引导线图像预处理前后的结果如图2所示。

图2 引导线图像预处理前后的结果Fig. 2 Results before and after preprocessing of guide line image

2 引导线边缘识别

由图2可知，经过模式滤波处理后的引导线，其灰度值明显区别于作为背景的周遭环境的灰度值，但还是不能满足小车智能识别的需要，需要对其图像进行分割。本文使用阈值分割法对目标图像进行分割，即通过最大化类间方差法［7-8］计算引导线与背景之间的方差，如式（2）所示。

式中：σ2为引导线与背景之间的方差；k为灰度级，取值范围为0～255；pA(k)为像素被分到前景的概率；mA(k)为前景的平均灰度；pB(k)为像素被分到背景的概率；mB(k)为背景的平均灰度；mG为整个图像的平均灰度值。

通过式(2)遍历0～255 个灰度级，求出引导线与背景之间方差σ2的最大值，此时的灰度级t即为分割引导线与背景的阈值。

以求出的阈值t为分界线，通过阈值二值化分割法，将引导线区域（前景）的像素置为255，引导线周遭环境区域（背景）的像素置为0，如式（3）所示。

式中：s(x，y)、D(x，y)分别为二值化分割前、后的灰度值。

引导线图像经过二值化分割后即可进行边缘检测。经常使用的边缘检测算法有Sobel算子、拉普拉斯变换、Prewitt 算子、Roberts 算子、Canny算子［9］等。由于含有引导线的输入图像有较少的道路边缘干扰，经过二值化处理后进行边缘检测时无需担心因阈值设置不合理而导致有效的边缘信息被去除；同时又排除了其他干扰，无需担心输入图像中的噪声干扰被视作边缘而不会被表示出来等问题，本文选用Canny 检测算子对二值化处理后的引导线边缘进行检测，结果如图3所示。

从图3可以看出，Canny算子能够很好地检测出道路引导线的边缘，满足智能小车视觉导引的需求。

图3 Canny二值化结果Fig. 3 Result of canny binarization

3 直线行驶视觉导引

直线行驶的小车引导线图像经Canny 边缘检测后得到引导线边界，再通过Hough 变换［10］检测引导线的直线边界，进而通过两边界线求得道路中心线，并与道路中心线的数学模型一起得到小车行进过程中的设定点与设定方向。

3.1 引导线边界拟合检测算法

运用Hough变换检测引导线边界的算法如图4所示，参数化引导如图5所示。引导线边界拟合算法流程如下：

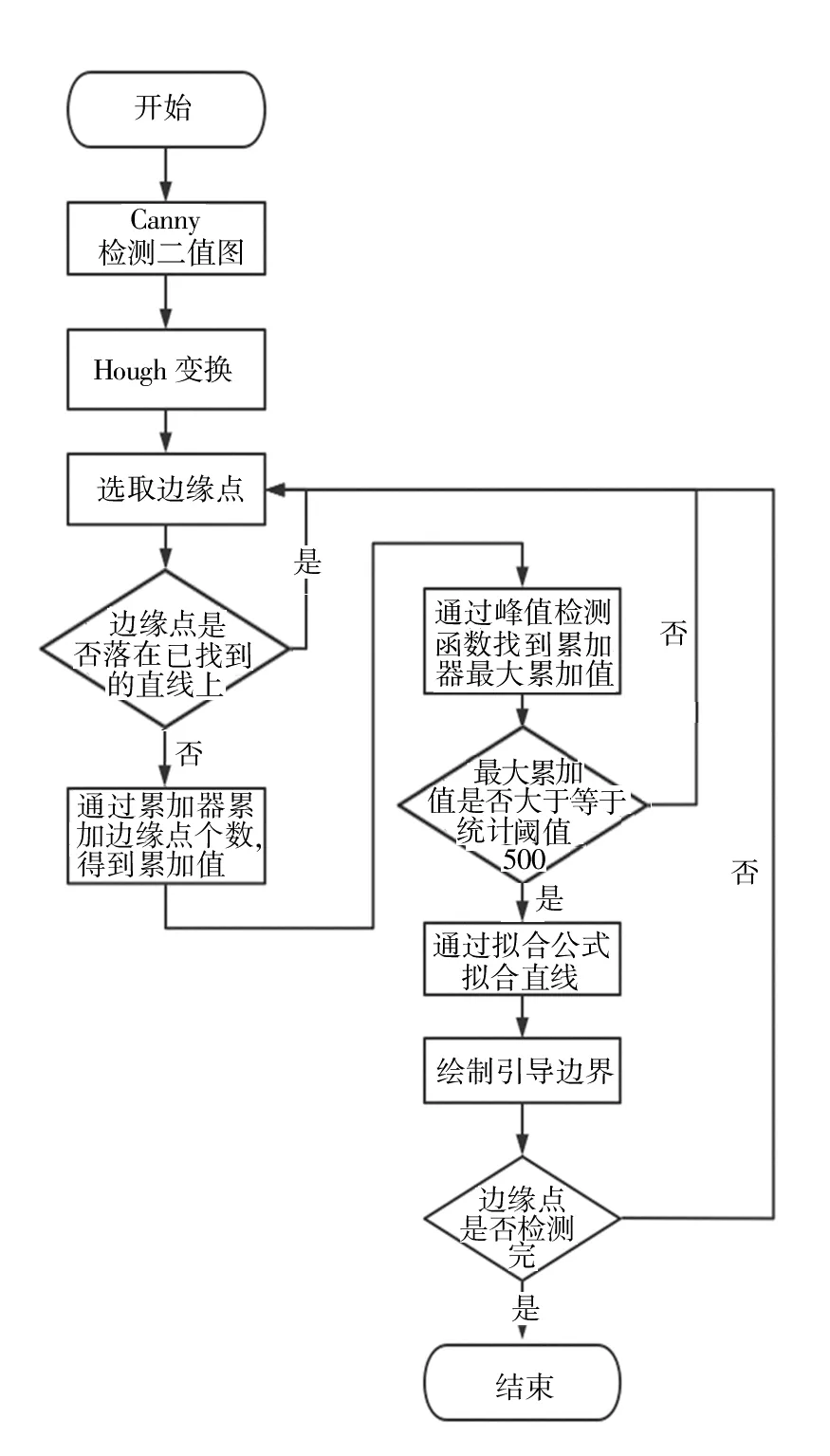
图4 引导线边界拟合检测算法Fig. 4 Detection algorithm of boundary fitting of line guide

（1）对图3 二值化结果进行Hough 变换，将其图像空间转换成参数空间。

（2）任意选取一个边缘点，如果该边缘点落在已经找到的直线上，则重新选择边缘点；否则，通过累加器累加边缘点个数，得到累加值。

（3）通过峰值检测函数找到累加器的最大累加值，与经统计得到的阈值500 相比较。如果累加值大于或等于阈值，则执行下一步；反之，返回步骤2重新选取边缘点。

（4）将找到的边缘点集通过拟合公式拟合，得到引导线的边界。

（5）将引导线边界绘制在图5 上，并判断边缘点是否全部检测。如果边缘点全部检测完毕，则流程结束；如果没有，则返回步骤2，重复选取边缘点，直至边缘点全部检测。

图5 引导参数化Fig.5 Parameterization of line guide

3.2 直线行走引导的参数化跟踪

直线行走引导的目的是让偏离引导线中心的小车，通过给定的位置修正小车行驶过程中的位姿偏差。

假定摄像头安装在小车的前方正中心，摄像机捕捉到图像的中心方向即小车的行驶方向。假定小车的初始位置为坐标原点(0，0)，观测点距离小车位置为R，以小车质心为圆心，观测点到小车质心距离为半径作圆弧C，如图5所示。

由于直线行走的小车其引导线边缘相互平行，假定引导线的两条边缘线方程分别为x1=k1× y1+ c1（直线1）、x2= k2× y2+ c2（直线2），则引导线的中心线到两边的距离如式（4）所示。

由式（4）可得道路中心线的方程为x = k ×y + xe- ye，该中心线与圆弧C 的交点即为小车的设定点(xe，ye)。智能小车行驶时只需要根据设定点的坐标，通过运动控制策略即可实现实时位姿控制。

4 弧线行驶视觉导引

对弧线引导的道路图像采用直线引导道路图像相同的预处理操作，得到经Canny 边界提取后的二值化图像，通过图像骨架提取算法提取弧线道路的中心线；以智能小车质心为圆心，质心与观测点之间的距离为半径作圆弧，中心线与圆弧的交点即为设定点；以设定点为圆心搜索弧形引导线轮廓边界到设定点的最小距离，该最小距离的垂线方向即为设定方向。

4.1 引导线图像骨架提取

弧线引导道路的中心线是弧线引导道路的中轴，也是智能小车行驶的最短路径，因此弧线引导道路的骨架提取问题本质上是最短路径规划问题。本文应用Astar 最短路径搜索算法对弧形引导线进行骨架提取，解决了骨架提取算法提取的骨架偏离引导线中轴的问题。骨架提取算法流程如图6所示。

图6 中，首先对Canny 检测后的二值图片进行距离变换，得到弧形引导道路的距离场，再经过分水岭算法获取含有引导道路的骨架潜在图；同时由主动轮廓模型确定引导道路的凸点，通过引导道路中心线端点到引导道路凸包的距离对引导线的骨架点进行筛选，得到骨架关键点；利用 Astar 算法搜索引导道路的骨架关键点，从而得到引导线的骨架，如图7所示。

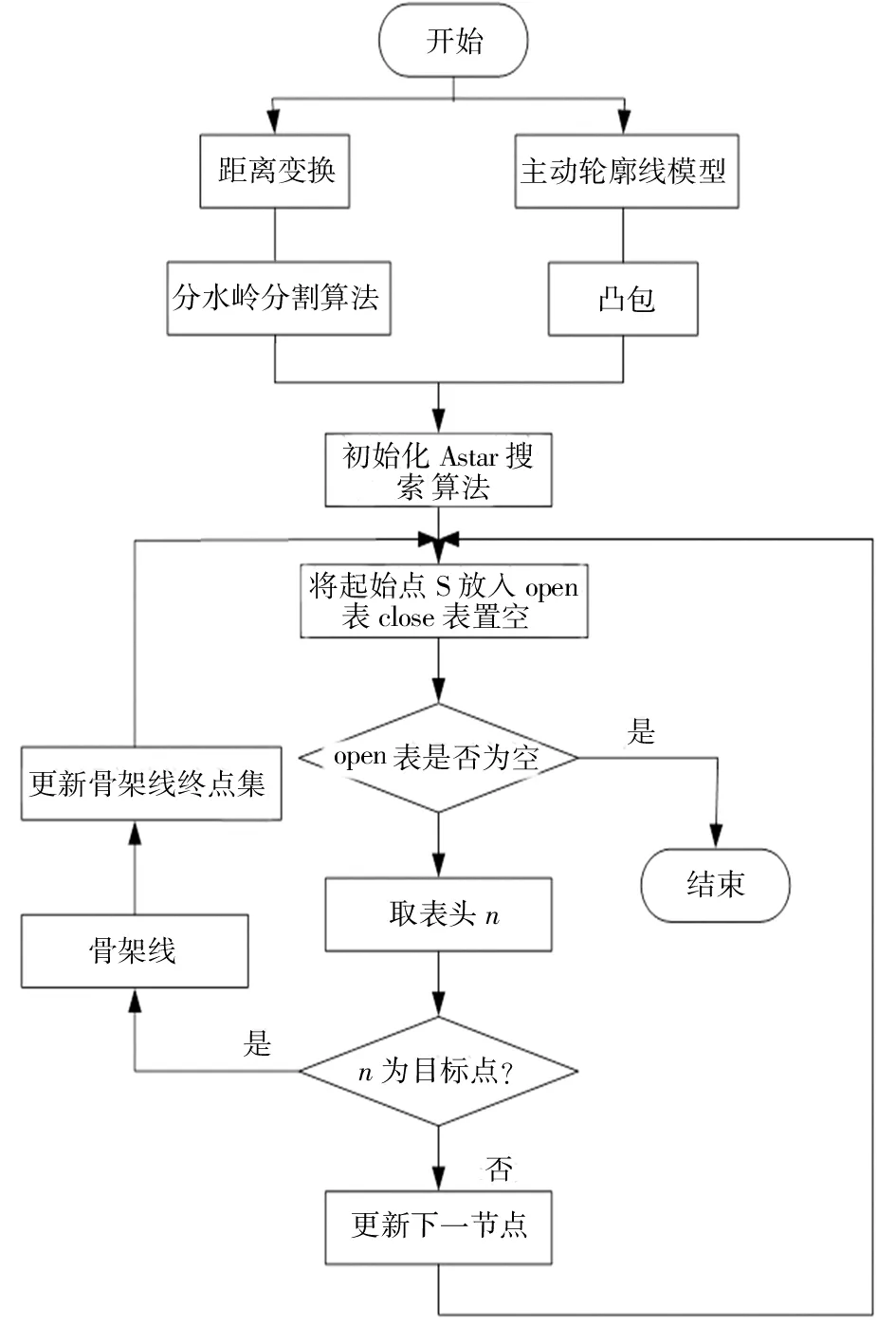
图6 骨架提取算法流程Fig. 6 Skeleton extraction algorithm flow

由图7 可以看出，通过此方法得到的引导线骨架十分接近引导线的中心线，说明基于Astar的骨架提取算法在弧形引导线的骨架提取中非常适用。

图7 弧形道路的骨架提取Fig. 7 Skeleton extraction of curved road

4.2 弧线行走引导的参数化跟踪

同直线行走引导相似，以智能小车质心为圆心，质心到观测点的距离为半径作圆弧D，圆弧D与弧形道路中心线即骨架轮廓线的交点即为智能小车的设定点，如图8所示。

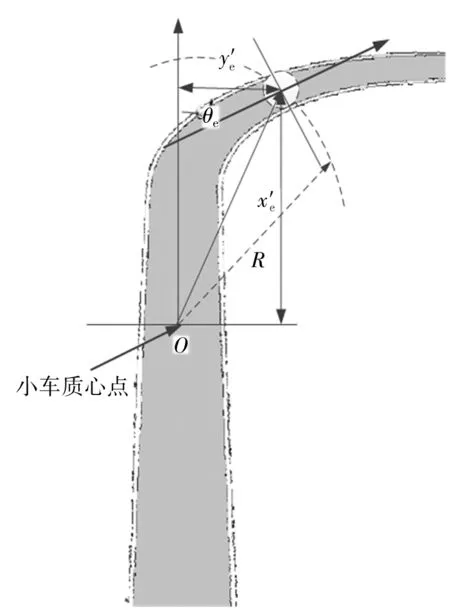
图8 弧形道路引导示意图Fig. 8 Schematic diagram of arc-shaped road guidance

由于弧形道路中心线没有一个通用的数学程式去建模，因此为简化算法，本文采用遍历的思想，以设定点为圆心，在道路区间找寻最大内切圆，从而求得设定点与两边界线距离和的最小值，如式（5）。

式中：(xl，yl)、(xr，yr)分别为小车的设定点(x′e，y′e)到左、右两侧边界线的交点。

由式（5）可以得到道路中心线的方程为x=k × y + x′e- y′e，该中心线与圆弧D 的交点即为小车的设定点(x′e，y′e)。智能小车行驶时只需要根据设定点的坐标，通过运动控制策略即可实现实时位姿控制。

5 结论

围绕智能小车视觉导引，采用C++编程辅以OPENCV 库处理图像，采用Hough 变换法、Astar骨架提取法找寻引导道路中心线；引入引导道路参数化模型，确定智能小车的设定点与设定方向。实验结果表明，提出的引导线参数化方法，降低了智能小车导引的复杂度，能满足具有规则引导线的智能小车的日间巡检。