基于免疫算法的电动自行车充电桩选址研究
杨佳奇 陈志涛 刘育源 肖静莹 王洁 熊 焱
(辽宁科技大学理学院,辽宁 鞍山 114051)
1 引言
因价格便宜,使用方便,电动自行车作为短途交通的代步工具深受人们的喜爱。截至2021年,我国电动自行车年销售量为3000万辆,社会保有量达3亿辆,并按每年30%的速度快速增长。伴随而来的不规范电引发的火灾等安全事故也屡见不鲜,因此建立社区内公共充电桩满足刻不容缓。如何合理对公共充电桩选址布局,满足居民充电需求,实现区域电动自行车的安全集中停放和充电,是社区、消防等部门急需解决的社会问题。
电动车充电问题不仅直接关系到使用者的安全、满意度,还与环保、节能等社会问题相关。目前针对电动汽车充电站选址问题研究比较充分,主要从使用者角度如距离满意度[1,2]、覆盖需求等[3],从投资者角度如建设成本、用户用电成本等[4],或者从决策评价角度[5,6]进行研究。电动自行车方面研究主要集中在共享单车停靠选址研究。Saharidis等[7]在考虑投资预算约束下,以最小化用户行走时间和未满足的停、取车需求为目标,建立公共自行车停车点选址和车辆及停车桩配置决策的多时段优化模型。由于电动自行车和电动汽车、共享单车停靠环境和充电方式等方面的差异,不能直接搬运套用适用于电动汽车的充电桩选址问题的研究成果,需要结合电动自行车充电实际进行研究。选址问题是一个组合优化问题,属于NP-hard问题,其求解方法主要有如遗传算法[8]、粒子群算法[9]等。免疫算法是(Immune Algorithm,IA)作为一种具有全局搜索能力的智能算法,能够解决进化过程中出现的局部最优解的问题,被广泛应用在经典优化问题中[10]。结合区域电动自行车分布情况,考虑充电站的覆盖率和电动自行车实际充电特点,本文建立了在满足居民充电距离和频次约束下的以建设总成本最小为目标的电动自行车充电站选址模型,并采用免疫算法对其求解,仿真结果表明方法是可行有效的。
2 模型建立
2.1 需求分析
通过对居民的电动自行车充电需求的问卷调研,可知我国南方大部分区域每个家庭大多会配备1到2辆电动自行车,且电动自行车每次充电时长与车辆行驶距离、电池容量等因素有关,每天充电的电动自行车数量相对固定,使用者通常会选择距离500米范围内公共充电站。
2.2 模型假设
同一需求点的所有车辆在同一时间段同时充电的概率很小,为保证同一需求点需要充电车辆在一天内都可以充电,引入充电需求满足系数a。定义为ti表示第i个需求点车辆平均充电时间(小时),0≤a≤1。在调研基础上,依据居民电动自行车充电最大服务距离、频次需求和区域场地条件,将整个服务区域划分为若干个需求点和备选点,并假设满足如下条件:
(1)每个需求点都可以成为建站点;
(2)每个备选点都满足居民充电需求且符合建设安全要求;
(3)不考虑充电站的建设等级,每个充电站的充电桩规格相同,服务能力无差异;
(4)需求点也是建站备选点,若第i个需求点建站,则该需求点的用户到站距离为0;
(5)若第i个需求点未被选址,则其用户可由与其距离小于可接受距离的另一个建站点j服务。
2.3 模型建立
其中m:需求点的个数;n:实际充电桩安装数量;dij:表示车辆从充电站i到充电站j的距离;Dj:表示需求点i可接受的最大服务距离;Ni:在第i个充点电服务的车辆数量;Xi:0-1决策变量,Xi=1表示第i个候选充电站投入建设;Xi=0表示第i个候选充电站不投入建设;pi:充电站i安装充电桩的个数;Ci:第i个充电站基础设施建设成本;C:单位充电桩安装、维护成本;(1)式为目标函数表示充电站总成本最小,第一个表达式表示基础建设总成本;第二个表达式表示充电桩安装、维护成本;(2)(3)式为约束条件,(2)式表示每个需求点在可接受距离范围内至少有一个充电站为其服务;(3)式表示在第i个充电站接收服务的车辆都能满足充电需求。
3 基于免疫算法求解模型
免疫算法是根据人体免疫系统的作用机理而形成的一种新型的智能优化算法[10],具有并行性、全局收敛性、自适应性等特点。
3.1 编码方式
每个抗体代表一个可行的电动自行车充电站选址方案,根据本文建模特点,采用字符编码方式,如有6个电动自行车需求点建立充电站的问题,1,2,…,6表示需求点序号,从中选出4个需求点建设充电站,抗体v=[6 4 3 1]表示在第6、4、3、1需求点建电动自行车充电站。
3.2 多样性评价
(1)抗体v-抗原亲和力:,当抗体v满足约束条件时,其亲和力Fv等于该抗体对应的充电站总成本,即对应的(1)式的值,否则等于一个很大的数C,本文中为2*e+5;
(2)抗体v-抗体t的亲和力:,其中kv,t表示抗体v-抗体t中相同的数字的个数,即可行解v,t中有几个相同的电动自行车充电站建站点,L表示抗体的长度;
(4)抗体v的期望繁殖率pv:由抗体与抗原之间的亲和力和抗体间的浓度共同决定,即
β为多样性评价参数。
3.3 免疫操作
(1)采用轮盘赌选择机制进行选择操作,选择概率即为(4)式计算得出的期望繁殖概率;
(2)采用单点交叉进行交叉操作;
(3)随机选择变异位变异。
免疫算法具体操作步骤如表1所示。

表1 免疫算法
4 仿真实验与分析
实验数据来源于江西省上饶市某封闭小区。该小区占地面积约为16万平方米,包括多层、小高层及高层住宅,约有1000户居民。根据调研该小区的每天需要充电电动自行车车数量、分布、充电站所含充电桩个数等信息由表2给出。
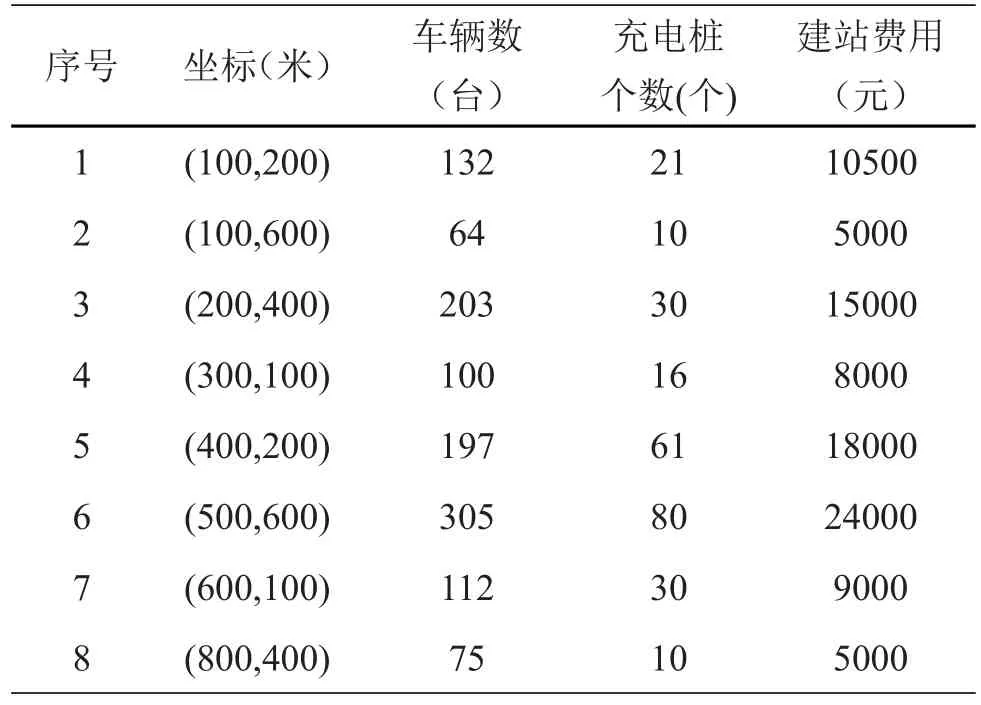
表2 需求点信息
根据本文提出的选址模型,按照免疫算法进行仿真求解。实验环境为Intel(R)Core i5-8400 CPU@2.80GH在,16GB内存,操作系统为64位Windows 10,使用Matlab2016b进行编程。算法参数分别为:种群规模100,记忆库容量20,迭代次数Maxgen=100,交叉概率0.1,变异概率0.4,多样性评价参数0.95,c=500元。
最大服务距离为500米、满足系数α=0.125时,免疫算法的收敛曲线如图1所示。
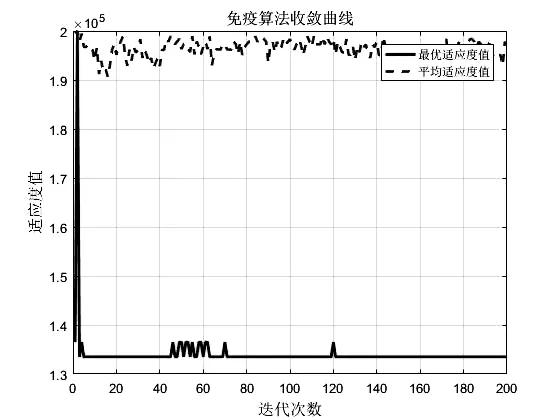
图1 免疫算法收敛曲线图
从图1可以看出,免疫算法在求解本模型整体来说是收敛的,此时最小成本为133500元。此时在1、5、6号需求点建站,使用者共有两种充电选择,第一种如图2所示:1号需求点建站,只对自己服务,4、7、8需求点在5号需求点接收服务,2、3需求点在6号站点接收服务;第二种:1号仍只为自己服务,2、4、7号需求点在5号需求的服务,6号还为3、8号需求点服务。也就是说对2、8号需求点来说,与5、6号充电站距离都在最大服务距离范围内,可选择性更多,被服务机会更大。
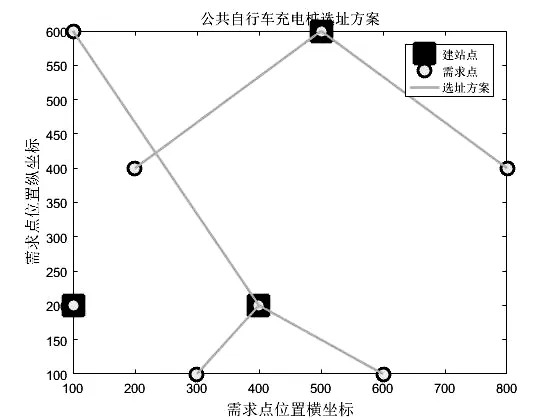
图2 选址充电方式一
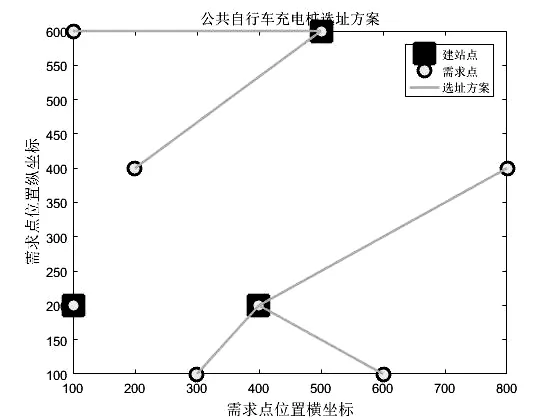
图3 选址充电方式二
当最大服务距离为500米,α=0.1时,免疫算法的收敛曲线及得选址充电方式如图4和图5所示。
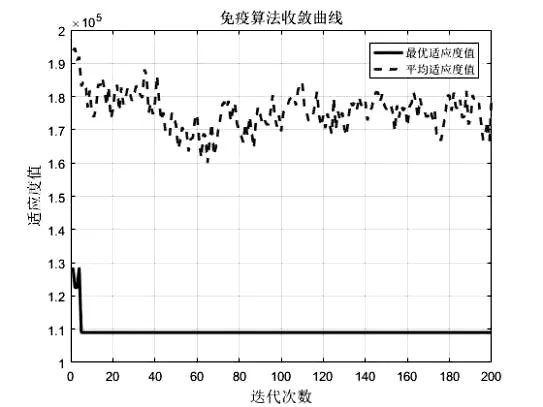
图4 免疫算法收敛曲线
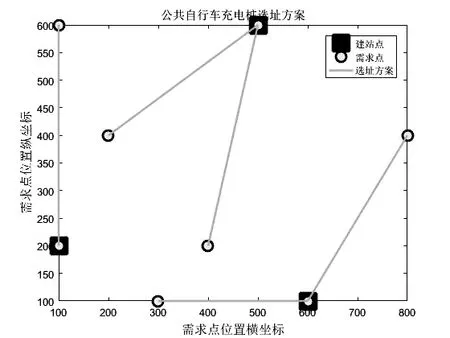
图5 选址充电方式
此时最小成本为109000元,从图5可以看出建站点为1、7、6需求点,其1,2需求点同时在1号站接收服务,3、5、6在6号站接收服务,其余的在7号站接收服务。
上述仿真结果表明:免疫算法在求解模型时收敛,而且能够较快地收敛到最优解。当最大距离不变时,充电需求满足系数α越小,即电动自行车充电时间越短,充电桩利用率越高,企业成本越小。在满足约束条件下,在含有充电桩个数多的需求点建站的可能性大一些。
5 结语
针对电动自行车实际充电情况,引入了充电需求满足系数α,建立了以满足充电需求条件下,企业最小成本为目标的数学模型,并利用基本免疫算法对所提模型进行求解,仿真实验表明本文建立的数学模型,能够客观描述电动自行车充电特点,设计的算法较为简单,具有很好的收敛性。对企业来说,适当增加充电插头,可以降低成本,提高利润。

