甲醇-柴油双燃料发动机甲醇泄漏故障预诊断研究

王涯鑫，李捷辉，王健

(江苏大学汽车与交通工程学院，江苏 镇江 212013)

随着石油紧缺形势的日益严峻和国六法规的出台，甲醇作为一种清洁燃料在发动机领域的应用日渐广泛。甲醇-柴油双燃料发动机能够灵活切换纯柴油和甲醇-柴油两种工作模式，具有动力性强、经济性好、炭烟排放少等优点，有很好的推广前景。然而甲醇腐蚀性较强，易腐蚀管路导致泄漏；且甲醇对人体有害，泄漏后可能造成不可估量的损失。现有的发动机故障诊断系统未对甲醇系统的故障进行监测，无法诊断供醇管道腐蚀状态并预测管道剩余寿命。而定期进行提前维护势必又会增加维修成本。因此，为提高双燃料发动机的安全性、降低双燃料发动机的维护成本，对甲醇管道腐蚀泄漏故障预诊断的研究具有重要意义。

近年来，燃料的泄漏问题备受关注，许多科研人员针对各种应用环境提出了不同的诊断方法。文献[3]通过压缩感知理论对天然气管道泄漏信号进行压缩采集，再结合一维卷积网络进行分类，完成了管道的泄漏孔径识别，并保证了较好的鲁棒性；文献[4]通过能量模式法提取管道振动信号特征，再用支持向量机进行特征识别，实现了对泄漏故障发生位置的准确定位；文献[5]通过经验模态分解和奇异值分解相结合的方法去除管道压力信号中的噪声干扰，提高了石油管道泄漏故障的诊断精度；文献[6]利用伯努利方程和气体压力常微分方程分析乘用车油箱压力波动，计算泄漏流量，较好地完成了对1 mm小孔以上泄漏的故障诊断。

然而，这些方法都存在一个共性问题：只能够检测已发生的泄漏故障，无法在泄漏发生前进行预测。甲醇不同于无毒燃料，其泄漏后易造成危害，需寻找一种方法能够在泄漏前进行预测，防止泄漏造成的损失。

概率神经网络(Probabilistic Neural Network，PNN)具有训练过程简单、收敛迅速、容错性强等优点，在发动机故障诊断领域有着广泛应用。文献[7]通过PNN分析发动机曲轴转角信号从而定位发动机失火故障，具有流程方便、操作简单的优点；文献[8]提出了一种基于粒子群算法的PNN用于诊断发动机传感器故障，仿真表明该方法能够有效地进行传感器的故障分类。

以上研究中概率神经网络展现出了良好的诊断性能，但是甲醇-柴油双燃料发动机与普通发动机相比，同时具有柴油、甲醇两套控制系统，结构更为复杂，这对PNN的诊断性能提出了更高的挑战。简单的PNN模型无法满足故障诊断精度和速度的要求，需要对PNN模型进行优化，提升其诊断性能。

近年来萤火虫算法(Firefly Algorithm，FA)理论的发展为基于神经网络的故障诊断提供了一种全新的优化方法。本研究以甲醇-柴油双燃料发动机为对象，针对现有故障诊断系统无法预测供醇管道腐蚀泄漏故障的问题，采用经验模态分解(Empirical Mode Decomposition，EMD)结合能量熵的方法进行振动信号的特征提取，解决了供醇管道振动信号非平稳、非线性，难以准确完整地提取特征的问题。通过基于萤火虫算法的概率神经网络(FAPNN)对振动信号的特征进行分析，识别供醇管壁厚度以判断腐蚀程度，再通过管壁厚度变化曲线预测出供醇管道的剩余寿命，从而获得最优的故障预诊断效果。

1 FAPNN故障预诊断模型研究

1.1 概率神经网络理论

概率神经网络(PNN)是一种基于统计原理的人工神经网络，是径向网络的一种，属于前馈网络。PNN一般包含以下4层网络结构：输入层、模式层、求和层以及输出层，如图1所示。

图1 概率神经网络结构

输入层不执行任何计算操作，只负责将特征向量传入神经网络，交给模式层的神经元。输入层的神经元个数与输入数据的维度，即样本特征的个数相同。

模式层负责计算输入特征向量与训练集中各个模式的相似度。每个模式层的神经元都有一个中心，该层接收输入层的样本输入，计算输入向量与中心的距离并将其送入高斯函数得到模式层的输出。模式层神经元的个数与输入的训练样本个数相等。

每个模式层神经元的输出为

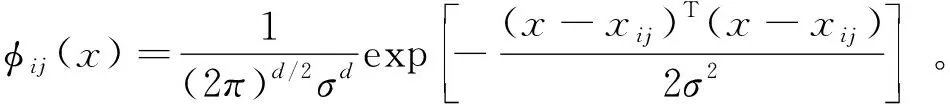
(1)

式中：为特征向量；为特征向量的维度；为平滑因子；为第个样本的第个中心。

求和层负责将每个分类的模式层的神经元连接起来，并对同一类别模式层神经元的输出加权平均，计算出每个分类的总概率。这一层的神经元个数为样本的类别数目，在本研究中即为故障类型的数目。

求和层输出的每个故障分类的概率为

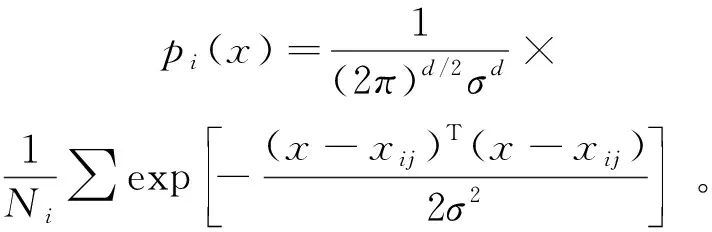
(2)

式中：为第类故障的样本总数。

输出层负责输出求和层计算出的概率最大的分类。具有最大概率的分类输出为 1，其他分类均输出为 0。

由上述可知，平滑因子是PNN的重要参数，选取合适的平滑因子对于PNN的分类准确性十分重要。本研究选择采用萤火虫算法(FA)寻找最合适的平滑因子，实现PNN的自适应寻优。

1.2 萤火虫算法理论

萤火虫算法(FA)是根据自然界中萤火虫群会向最亮的个体聚集的现象而提出的。在FA算法中，每个萤火虫的位置代表一个所求问题的解，在本研究中代表PNN的平滑因子的一个取值。萤火虫的亮度则代表该解的适应度，亮度越高表示该解越接近最优解。每个萤火虫会向着亮度比它更高的萤火虫移动，亮度越高的萤火虫对其他萤火虫的吸引力越大。最终所有萤火虫都会聚集到亮度最高的萤火虫的位置，此时的最亮位置即为问题的最优解，由此完成自适应寻优的过程。对于FA算法，有以下定义式：

在维解空间内，每个萤火虫的位置定义为=(,,…)。

萤火虫与萤火虫之间的吸引力定义为

()=(-)-+。

(3)

式中：为最大吸引力；为最小吸引力；为光吸收系数；为两只萤火虫的空间距离。

萤火虫会随迭代次数向更亮的萤火虫移动。迭代后萤火虫的空间位置定义为

(+1)=()+
()[()-()]+。

(4)

式中：为萤火虫算法的迭代次数；为随机扰动；为扰动的步长系数。

1.3 基于萤火虫算法的概率神经网络模型

为实现PNN模型的平滑因子的自适应寻优，提升其故障预测性能，本研究将平滑因子的取值作为萤火虫算法的优化对象，建立基于萤火虫算法的概率神经网络模型(FAPNN)，模型具体流程见图2。

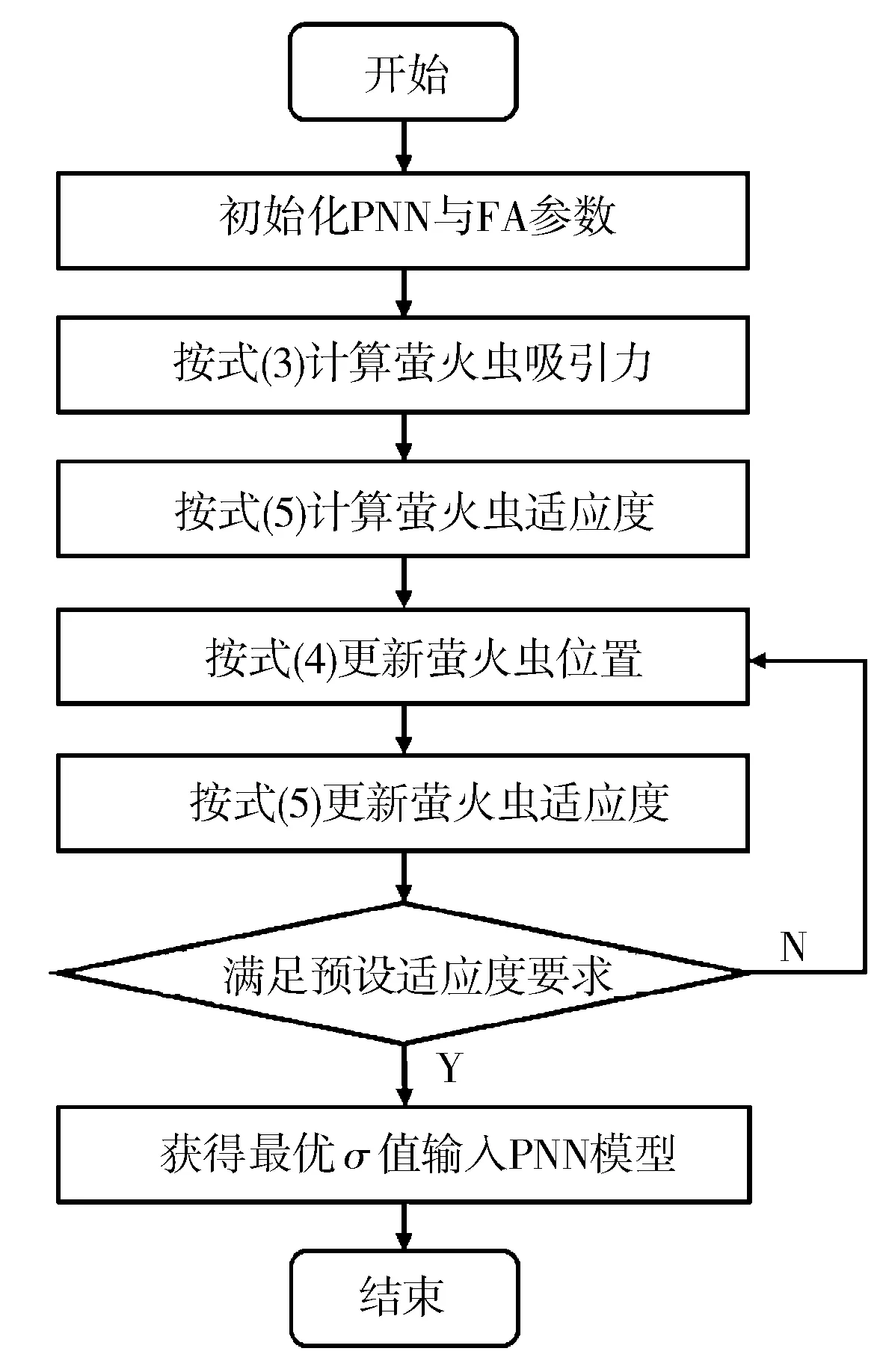
图2 FAPNN诊断模型流程

1) 设定萤火虫算法的种群个数、步长、最大吸引力、最小吸引力。将PNN的平滑因子作为萤火虫的初始种群，随机分布萤火虫的初始位置。

2) 计算当前每个萤火虫的适应度。其中，用模型的预测错误率作为FA算法的适应度函数，其定义式为

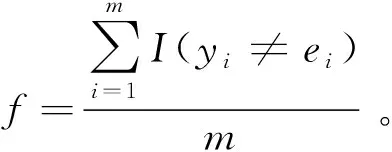
(5)

式中：为输入的样本个数；和分别表示PNN的预测结果和样本的实际值。(≠)代表预测结果和样本的实际值不相同的次数，即误判次数。适应度值越接近0说明FAPNN模型误判率越低，适应度越优，萤火虫的亮度越高。

3) 根据式(3)计算当前每个萤火虫的吸引力。

4) 根据式(4)更新萤火虫的空间位置。

5) 根据式(5)计算每个萤火虫位置更新后的适应度值。若适应度满足预设的适应度要求或算法已到达最大迭代次数，则跳转到步骤6，否则跳转到步骤4。

6) 输出最终的萤火虫的位置作为平滑因子的最优解输入到PNN模型中，完成自适应寻优。

2 供醇管道故障预诊断应用

根据上述理论模型，本研究提出了一种基于EMD分解和FAPNN模型的甲醇-柴油双燃料发动机甲醇泄漏故障预测方法，流程见图3。

1) 对供醇管道振动信号进行EMD分解，得到信号的各模态分量。

2) 计算每个模态分量的能量熵作为信号特征，构建特征向量矩阵。

3) 将特征向量矩阵输入FAPNN预诊断模型中，识别出供醇管道当前壁厚，并判断管道的腐蚀故障状态。

4) 结合当前壁厚，根据管壁厚度变化曲线预测出供醇管道的剩余寿命。

图3 故障预诊断流程

2.1 试验数据来源

为验证本研究所提方法的有效性，通过台架试验采集发动机振动信号作为故障样本数据并进行处理和分析。

试验中使用的甲醇-柴油双燃料发动机在4G33TC柴油机上加装甲醇系统改装而成(见图4)。三向加速度传感器PCB 356A32安装在供醇管道的正上方，传感器安装位置见图5。使用LMS SCADAS Mobile SCM05动态信号分析仪控制数据采集，并将采集到的信号存储到计算机中进行分析。

图4 甲醇-柴油双燃料发动机试验台架

图5 加速度传感器安装位置

根据国标GB/T 3093—2002并结合本研究发动机供醇管道的工作环境，将管道状态分为正常状态和三种不同程度腐蚀状态，具体参数见表1。通过改变供醇管道的管壁厚度，模拟了管道在不同腐蚀状态下的振动信号。为验证本研究诊断方法在各种工况下的普适性，选择发动机分别在1 200 r/min，1 600 r/min，2 000 r/min，2 400 r/min 4个工况下进行信号采集，信号采样频率设置为10 240 Hz。为保证样本数量满足神经网络模型的训练和验证精度要求，4个工况下每种状态类别采集50组数据，共有800组数据样本；每组2 048个数据点，包含至少一个以上的工作循环。其中70%的数据，即560组样本用于训练神经网络模型，剩余的30%数据，即240组样本用于验证。

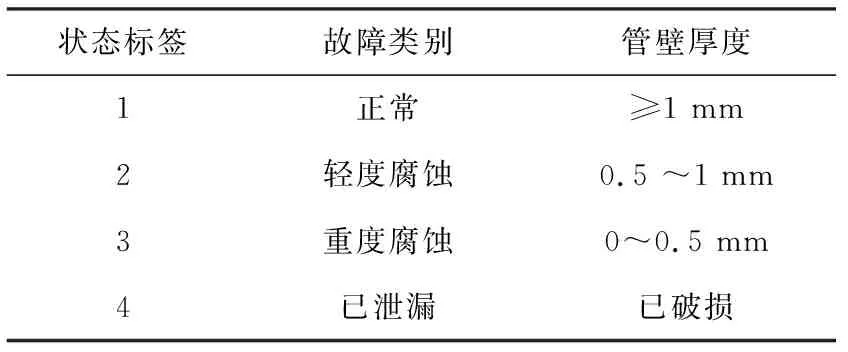
表1 供醇管道故障状态及对应参数

2.2 信号处理和特征提取

图6示出了1 600 r/min工况下发动机供醇管道在正常、轻度腐蚀、重度腐蚀、已泄漏这4种运行状态下的振动信号时域图。其中，状态1～4分别对应的供醇管道壁厚为1.5 mm，0.8 mm，0.4 mm以及在0.4 mm壁厚时钻孔获得的已泄漏状态。由图可知，虽然各信号之间都存在一定差异，但是难以准确分辨各信号特征的区别。因此，采用EMD将振动信号分解为多个本征模函数(Intrinsic Mode Function, IMF)并进行分析，提取能量熵作为信号特征。

图6 供醇管道振动信号时域图

图7示出轻度腐蚀(状态标签2)故障信号的EMD分解结果。从图中可以看出原始振动信号经EMD分解得到的各IMF分量的波形呈现不同的分布规律，且各模态分量的频谱存在显著区别，说明原始振动信号的有效成分被完整提取出来且不存在混叠现象。

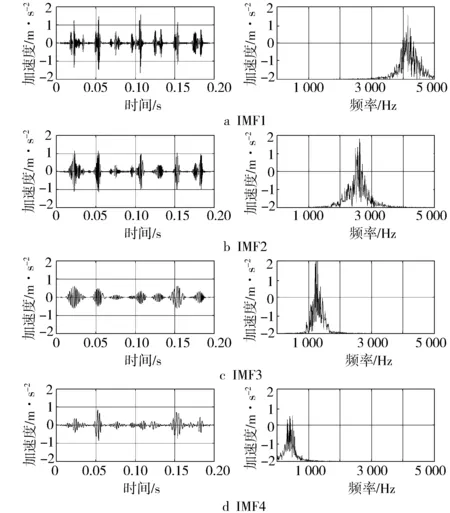
图7 EMD分解的各模态分量及对应频谱

能量熵作为一种量化信号信息的方法，可以准确有效地用于提取振动信号特征。计算每个IMF分量的能量熵作为故障特征向量，能量熵定义式为

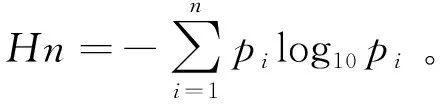
(6)

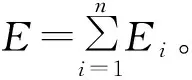
第个IMF的能量为

(7)

表2示出供醇管道在不同状态下各IMF分量的能量熵值。其中，H1～H4分别代表IMF1～IMF4时域信号的能量熵。由表可知，管道在不同腐蚀故障状态下对应的能量熵能够体现出明显差异，其中，正常状态下的能量熵相较于其他几种状态较小，已泄漏状态下的能量熵明显高出其他3种状态。

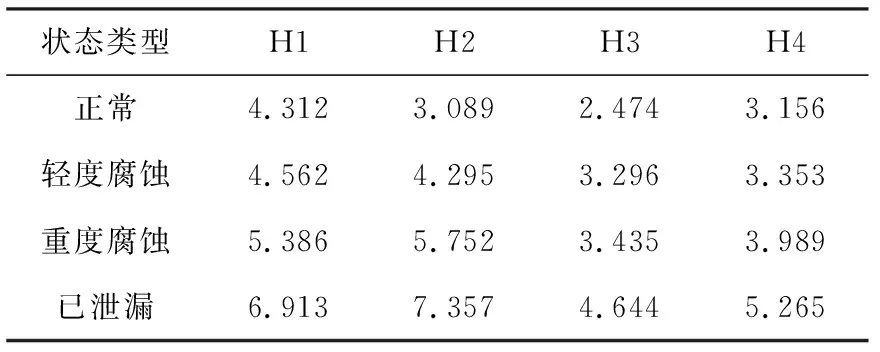
表2 各故障状态对应的IMF分量的能量熵

将每种故障状态类型与其IMF分量的能量熵一一对应构建成为4维的特征向量作为样本集合，并随机分为两个子集：训练集(每种状态70个样本)和测试集(每种状态30个样本)，作FAPNN故障预测模型的输入。

3 试验结果及对比分析

3.1 故障分类预测结果

在Matlab 2018b中建立FAPNN故障预诊断模型，将训练集样本输入模型中进行训练学习。其中，萤火虫算法的种群个数=40，移动步长=02，最大吸引力=1，最小吸引力=005，光吸收系数=1，最大迭代次数设置为100，适应度阈值为0.05。萤火虫算法的适应度随迭代次数变化曲线见图8。

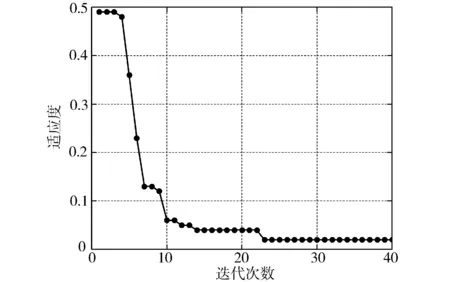
图8 萤火虫算法的适应度曲线

由图8可知，萤火虫算法适应度在迭代初期下降很快，在15代左右到达第一个平稳值，这代表算法陷入了局部最优解。但是在若干次迭代后适应度又下降了，并最终在24次迭代时稳定在全局最优解。这表明萤火虫算法具有很好的跳出局部最优的能力。

优化过程完成后，FA算法求得最优平滑因子=0.16。将其带入PNN中，按前述流程完成对FAPNN模型的训练，获得最优的故障预测模型。再将每种转速60组，共240组测试样本输入训练好的概率神经网络故障预测模型中，获得相应的分类结果(见图9)。

图9 FAPNN模型故障预诊断结果

由图9可知，在1 200 r/min和2 400 r/min的转速工况下，FAPNN模型能够准确识别出供醇管道的故障状态，准确率高达100%。在1 600 r/min和2 000 r/min的工况下，分别有两组和三组样本出现预测错误，准确率分别为96.7%和95%。综合4种工况准确率取平均值，全工况下FAPNN模型的故障预测准确率为97.9%，满足预设误差要求。

3.2 故障时间预测及验证

在通过FAPNN模型判断出管壁厚度的基础上，通过甲醇对管道的腐蚀速率推算出泄漏发生的准确时间。文献[15-16]对甲醇的腐蚀速率进行了研究，但试验环境及对象与本研究有所区别，无法用于本研究。为获得甲醇腐蚀速率的准确值，在双燃料发动机台架上对供醇管道进行甲醇腐蚀试验，采用M100工业甲醇装满管道，管口密封隔绝空气，每5 d，即120 h记录一次管壁厚度数据，共记录210 d，即5 040 h，43组数据。制作出管壁厚度随腐蚀时间变化曲线。部分数据见表3。

表3 管壁厚度随时间变化数据

由表3可知，甲醇对供醇管道腐蚀速率为非线性，无法用平均速率进行计算。所以需要一种算法能够准确拟合并预测该腐蚀曲线。本研究提出的FAPNN神经网络不仅可用于状态分类，亦可用于数值预测。

图10示出FAPNN、BPNN和多项式函数对腐蚀曲线进行拟合预测的结果。其中，前3 000 h为拟合值，后2 000 h为预测值。可以看出，3种算法在拟合阶段均能较好地模拟壁厚变化曲线，但在进入预测阶段后，BPNN和多项式函数的预测结果均与实际值有一定程度的偏离，而FAPNN模型的预测值与实际数据拟合度较高，可以作为管道剩余寿命的预测依据。

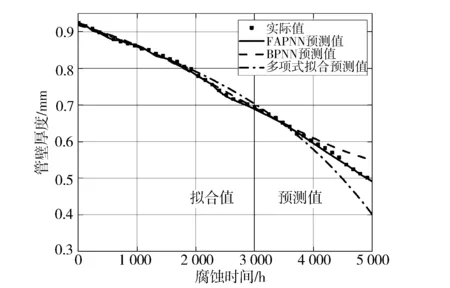
图10 FAPNN预测结果与实际值对比

根据FAPNN模型预测出的管壁厚度变化曲线，预测出供醇管道壁厚将在第4 891.2 h降至0.5 mm以下，进入重度腐蚀状态。实际试验结果显示，第4 920 h甲醇管道厚度降至0.5 mm，发出重度腐蚀预警，与预测时间相差28.8 h，证明了提出的方法在供醇管道寿命预测方面的可行性。

3.3 对比分析

为了进一步说明所提出的故障预测方法的有效性和优越性，分别采用较常用的粒子群算法(Particle Swarm Optimization，PSO)、遗传算法(Genetic Algorithm，GA)、烟花算法(Firework Algorithm，FWA)优化概率神经网络，并将故障预测结果与本研究所提出的FAPNN模型进行比较分析。每种算法的参数设置见表4。

表4 各算法的参数设置

将560组训练样本分别输入以上4种算法优化的PNN故障预测模型中进行训练，图11示出各算法的错误率收敛曲线。由图可知，训练初期FAPNN的收敛曲线最陡，这代表FAPNN的收敛速度最快。迭代至100次后仅有FAPNN与FWAPNN的错误率小于预设阈值0.05，而其他两种算法远未达到预设要求。此外，FAPNN的收敛曲线是所有方法中最低的，这表明其在搜索全局最优解时具有最佳性能。

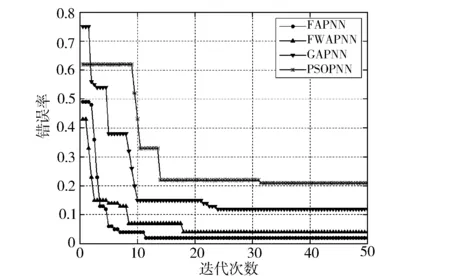
图11 各算法的错误率收敛曲线

为进一步探究本研究的预诊断模型在预测准确率和响应速度方面的性能，将各转速下共240组测试集样本输入上述4种故障预测模型中，记录训练时间和准确率并求平均值，结果见表5。

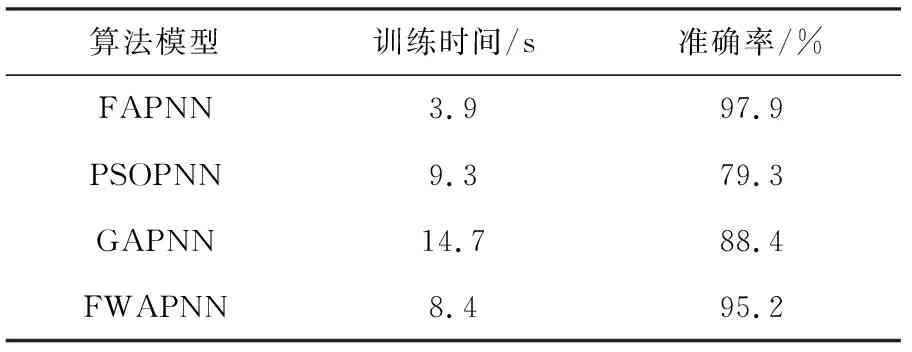
表5 各算法的运算时间与准确率

由表5可知，基于FA的PNN模型故障预测准确率最高，达到了97.9%，比基于PSO，GA和FWA的PNN模型分别高出18.6%，9.5%，2.9%。虽然FWAPNN的预测准确度与FAPNN相近，但是在训练速度方面FAPNN远超其他算法模型，仅需3.9 s，充分证明本研究提出的双燃料发动机腐蚀泄漏故障预测方法是可行且有效的。

4 结束语

EMD分解结合能量熵的方法可以有效完整地提取出发动机甲醇管道振动信号特征，且各特征之间无混叠情况，便于后续预诊断模型的识别分类。

针对PNN的平滑因子需人为设置，工作量大且准确率不高的问题，提出了FAPNN模型，通过萤火虫算法自适应寻找的最优解。试验证明，提出的FAPNN模型通过对供醇管道振动信号特征的识别，可以成功诊断出管道的腐蚀程度；再结合供醇管道壁厚变化曲线，能准确预测管道的剩余寿命，在泄漏故障发生前进行预测诊断，避免了甲醇泄漏造成的损失和危害，降低了甲醇-柴油双燃料发动机的维护成本。