可靠度区间维护与调度集成优化

赵 起，徐建萍，刘利显

(1.贵州大学管理学院，贵阳 550025;2.北京兴油工程项目管理公司,北京 100000)

0 引言

作为国民经济的产业支柱之一的制造业正向低成本、高可靠度、更安全高效的方向高速发展。本文以复杂机械产品加工系统中的柔性作业加工设备作为研究对象。设备的扰动直接影响着企业的生产效率。在实际生产中，机械故障是最常见的扰动因素，比起设备的故障后维修，预防性维护将更合理、有效。设备维护管理在经历不断发展后，衍生出基于设备状态的预测性维护方案，通过对设备状态未来趋势的预测，能够更加准确地对设备状态进行判断并对未来维护方案的生成提供有效支撑。

YALAOUI等[1]采用周期性的预防性维护策略，解决生产与维护集成问题，但周期性维护会导致设备的过度维护和维护不及时等问题。TLILI等[2]以平均维护成本为优化目标，通过设备可靠度对设备状态进行评价，采用设备使用寿命和受冲击次数是否达到阈值的维护策略。

将生产调度和预维护集成优化也逐渐成为制造领域的热点研究问题[3-5]。在柔性作业车间调度(flexible job-shop scheduling problem,FJSP)问题中，如何根据设备状态的诊断与预测选择出鲁棒性高、时间短的调度方案就尤为重要。杜阳宇等[6]提出了基于设备可靠度的预防性维护策略，同时考虑设备退化。张国辉等[7]提出了预调度与实际调度最大完工时间偏差和每台机器空闲时间和机器负荷的比值两个鲁棒性目标，并通过仿真可以有效减少工序延误。路光明等[8]将柔性作业车间的鲁棒性调度与预防性维护的联合决策模型,提出一种基于空闲时间段的插入是维护策略，优化目标为加工周期、机器可用性和调度方案的鲁棒性，并通过NRGA(non-dominated ranked genetic algorithm)进行求解，但其整个调度方案中寻找空闲时间段并不合理。

然而上述文献很少考虑将设备状态与故障率联系起来，仅仅对设备故障曲线的拟合并不能对设备的实时故障率准确反映。并且以往的维护策略也并不符合柔性车间的特点。鉴于此，本文提出基于设备健康状态的评价模型，可靠度区间维护策略，构建集成优化模型。进行多目标最小化最大完工时间和各工序预调度与实际调度的偏差时间优化，并通过NRGA进行求解，从而有效提升生产效率。

1 设备健康状态

1.1 设备健康状态评价模型

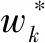
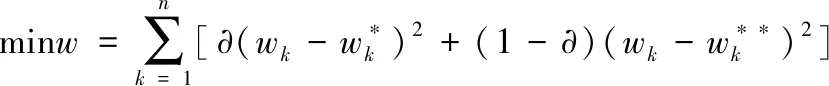
(1)

式中，∂为主客观权重的偏爱系数。本文将设备健康状态指数记为HV，并规定HV的取值范围是[0 1]，HV越接近1表示设备状态越好，越接近于0表示设备状态越差[9-10]。如若出现宕机或者故障，其中的某项指标将偏离正常值，因此,设备健康状态是对相关指标与其期望值偏差程度的体现，其计算规则：在某一时刻，测量值超正常运行极限值时，健康指数为 0，表示设备宕机，应即刻停机检修；在另一时刻，测量值等于标准值，健康指数为 1，表示设备运行状态最优。为消除指标间的量纲，如下所示对指标数据进行消钢处理：

(2)

(3)

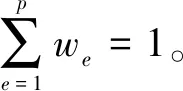
对于设备老化的健康状态，本文引用了欧美地区广泛应用于设备状态评估的老化健康指数经验公式[11-12]，如式(4)所示：

HV2(t)=1-(1-HV0)expB(t-t0)

(4)

式中，t0为新设备初始投运时间；t为设备被评估时对应工作时间；B为老化系数；HV0为设备在t0时间的初始老化健康指数，可以取多台同类型新投运设备健康指数的平均值。

设备健康状态一方面受到相关参数偏差程度的影响，另一方面受设备老化因素的影响，因此设备健康综合评估表达式如式(5)所示：

(5)

1.2 基于设备健康状态的设备故障率计算

为了能够正确预测设备维修的时间点和维修策略，就不得不考虑设备故障率的因素。因设备故障率与健康状态指数是互补关系。根据国内外研究，设备故障率与健康状态指数通常呈指数关系[13]。

λ(x)=KeC·HV

(6)

式中，λ为故障率；HV为设备健康指数；K和C分别为比例系数和曲率系数。对比例系数K和曲率系数C的求解可以根据历史数据反推得到。

2 基于威布尔函数的设备可维护区间

实践证明大部分机械设备故障率随时间变化呈浴盆曲线规律，设备故障率分为三个阶段，第一阶段为早期失效期，由于这一阶段一般为设备调试阶段，本文不考虑。第二阶段为偶然失效期，在这一阶段设备失效率较低也较稳定，可以将故障率近似看作一个常数，本文也不考虑。第三阶段是耗损失效期，设备由于老化等原因导致的故障率随工作时间的急剧上升期。从浴盆曲线中得知设备的最佳预防维护时间周期应为耗损失效期中的的一段曲线。如图1所示设备维护区间为可靠度[RF,Rp]区间对应的[tp,tF]时间段。

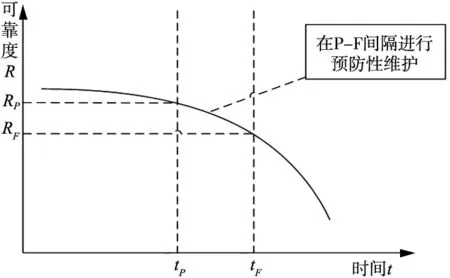
图1 设备维护曲线

设备故障率与分布函数的关系密切，不同的分布函数对设备故障率的分布一般都有着一定的差异。在现今较为常见的分布函数如指数分布、正态分布和威布尔分布中，指数分布和威布尔分布在可靠度的分布中得到拟合应用[14]。因威布尔函数对浴盆曲线的拟合度更高，可以将不同时期的分布函数进行准确描述。本文采用威布尔函数与设备故障函数进行拟合。

(7)

式中，β为形状参数；η为尺度参数；λ(t)为设备故障率随工作时间变化函数。根据威布尔故障率函数可知，当β<1时，瞬时失效率呈递减趋势，服从早期失效期的正态分布，偶然失效期服从β=1的情况，耗损失效器服从β>1的指数分布，浴盆曲线得到很好地拟合。因考虑设备老化本文只对耗损失效期进行分析。对形状参数β和尺度参数η的求解，最小二乘法和极大似然估计法都有着很好的应用。针对两种方法的选取通常有着不同的约束：秩回归法-最小二乘法适用于完全数据、小样本，极大似然法适合删失数据、混合数据和大样本(30+)。本文选取最小二乘法进行回归分析求解。

(8)

通过威布尔可靠性函数R(t)的变形并利用最小二乘法，对历史数据线性拟合，得到直线的斜率就是威布尔函数中的形参β，而y轴上62.3%所对应x轴上的时间点就是特征寿命或尺度参数η。有了β和η的数值就可将故障率函数与浴盆曲线进行拟合。

3 维护策略模型建立

维护策略的选择按程度分为最小维修、完全预防性维修和不完全预防性维修[15-16]。最小维修指设备发生故障时的维修，设备经过最小维修后只恢复到故障前状态。完全预防性性维修是设备故障之前进行更换维修，设备恢复未工作之前的状态。不完全维修为介于最小维修和完全预防性维修之间的维修程度。在实际生产中，维修为不完全维修。本文在考虑不完全维修的情况下，引入改善因子对设备不完全维修后的设备状态进行描述，即设备的有效工龄。

3.1 不完全维护的设备描述

在实际生产中，随着维修次数的增加，被维修设备因设备老化和不完全维护等原因，可靠度并不是呈线性递减的趋势。为了更好地描述设备在预防性维护中的实际情况。常用两种改善因子[17-18]，故障率递增因子b(q)与役龄递减因子a(q)。夏唐斌等[19]在文献[18]的基础上提出了结合两种调整因子的预防性维护前后的设备故障率函数。

λq+1(t)=bqλq(t+aqTq),t∈(0,Tq+1)

(9)

式中，λq为设备在第q个维护周期后的故障率函数；Tq表示两次维护的时间间隔；t表示设备运行加工时间周期内的起始运行时间。将调整因子结合威布尔故障率函数为:

(10)

式中，aq和bq可以通过历史数据得到。则设备第q+1个不完全维护周期的失效率为:

(11)

3.2 模型假设

本文进行如下假设：

(1)每次维护只有完全预防性维修和不完全预防性维修两种选择；

(2)完全预防性维修和不完全预防性维修的维修时间固定；

(3)对更换的设备残值不予考虑；

(4)不同机器因工作时间不同，同一时刻设备健康状态可能不同；

(5)维护操作只能在设备加工本道工序后进行。

3.3 模型建立

本文通过将机器拟化成Agent如图2所示，假设机器智能体能够对自身状态的实时监测，并具备本地计算能力，通过对自身健康指数的计算和对未来可靠度的预测，对达到可维护周期阙值的时间前进行交流共享给控制智能体。控制智能体通过多个机器发来的可维修策略进行整体维修策略的选择。

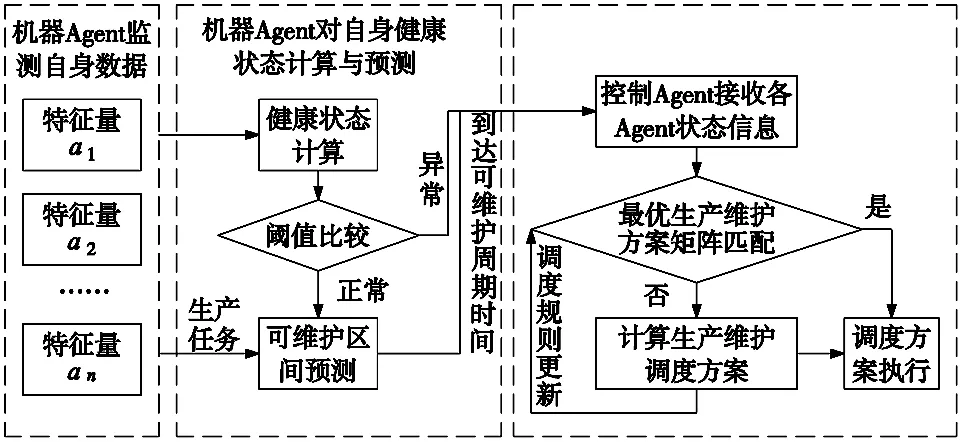
图2 流程图

鲁棒性指标最小化最大完工时间偏差最小和稳定性指标各工序预调度与实际调度的偏差时间最小为优化目标。由假设可知：

(1)维护策略学习模型

针对基于设备健康状态得到的设备可维护区间，由于柔性作业车间同一时刻设备加工时间不同的特点导致不同设备在同一时刻的实际役龄不同，这就导致每个设备的可维护时刻不同，因此对每个设备的从多个可维护时刻中选择最合适的时刻并选择出相应的维护方案将是一个维数灾难问题。而Q-learn算法结合了马尔科夫决策和蒙特卡洛算法的优点，通过不断采样更新的方法将无模型问题转化为有模型的强化学习问题，能够很好地解决此问题。因此本文选择通过Q-learn算法对维护方案进行选择。

Q-learn算法是基于TD-learning的强化学习方法。任务执行者即决策者根据环境感知当前状态，并根据当前状态进行动作选择，策略就是根据状态对动作空间映射的交互。对于每个决策可以根据回报反馈给决策者一个奖励值和新的状态，决策者根据新的状态再决定对新的动作的选择，如此循环往复。决策者的目标是在与环境的交互过程中获得最大的总奖励的期望值。

(12)

式中，S表示状态集合；s′表示状态s的下一状态；p表示状态转移概率；r0表示状态转移的即时回报；γ为折扣因子；Vπ(s′)为下一状态的值函数；根据每一状态值，结合具体动作通过ε-greedy对环境进行探索，并基于增量更新函数：

Q(S,A)=Q(S,A)+α(Rt+γmaxA′Q(S′,A′)-Q(S,A))

(13)

不断地对动作状态价值函数进行更新直到收敛。最优策略即为π′(s)，

π′(s)=argmaxAQ(S,A)

(14)

(2)鲁棒性最大完工时间建模

工件j的第h道工序开始加工时间和完工时间表示为：

(15)

加工工序Ojh的设备故障次数表示为：

(16)

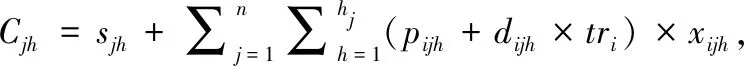
(17)

式中，Tz1和Tz2分别表示不完全维护和完全维护时间;Okl为机器i加工工序Ojh的前一道工序;Cjh为工序Ojh的完工时间；tri表示每次故障维修时间。

f1(x)=Cmax=max(Cjh),j=1,2,3,…,n

(18)

(3)稳定性工序偏差建模

(19)

(4)集成模型

对于多目标优化问题求解，往往采用加和组权法、层次分析法等方法将多目标问题转化为单目标进行求解。则目标函数为：

min(Makespan)=min(Cmax)

(20)

min(Deviation)=min(Z)

(21)

(22)

(23)

(24)

(25)

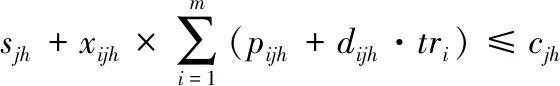
(26)

cjh≤sj(h+1),j=1,2,3,…,n;h=1,2,3,…,hj-1

(27)

(28)

sjh≥0,Cjh≥0,j=1,2,3,…,n;h=1,2,3,…,hj

(29)

式(22)和式(23)表示每一个工件的先后顺序；式(24)表示机器约束，即同一时刻同一道工序只能且仅能被一台机器加工；式(25)表示各个参数变量是正数。

4 模型求解

因多目标问题的目标间可能存在着矛盾和不可公度问题，传统的目标规划、层次分析法等将多目标化为单目标的这种归一化方法虽然能够对问题简化处理，但对目标的权重评定较为主观。而且此类方法往往只能得到一个解，并不能应对实际生产中决策者想要在多种方案选择其一的需求。因此本文选取多目标优化遗传算法NRGA，其是一种与NSGA-II仅仅在选择操作不同的非支配排序遗传算法。NRGA不仅保留了NSGA-II的全局搜索够力，而且通过引入轮盘赌的选择方法能够更快跟合理地收敛并将解保留下来。

4.1 编码和解码

染色体编码是遗传算法的重要环节之一，好的编码策略能够在寻找最优解时节省大量时间。本文借鉴文献[20]和文献[8]的编码方法采用基于工序和设备前两层基因编码方式，第三层基因为维护工序的记录。每层基因长度均为总工序长度。

第一层基因是加工工序的选择。对于工序的选择采用自然编码，根据每个工件出现的次数判断加工的工序为第几道。如基因段[3 1 2 1 3 5 4]依次表示工序为O31,O11,O21,O12,O32，O51,O41。

第二层基因是加工设备的选择。对于设备的选择采用自然编码，基于工序基因段确定机器选择。如设备基因段[1 3 4 3 2 5 2 1]对应工序选择依次表示为工序O31选择机器1加工、工序O11选择机器3加工，工序O21,O12,O32,O51,O41依次选择机器4,3,2,5,2,1。

第三层基因表示设备在可靠度区间内维护时刻和维护方案的选择，本文选择基于Q-learn算法对设备维护策略进行选择，并根据维护方案进行修正调度，本文采用右移调度规则来修正插入维护活动的不可行调度。最终结果对维护方案进行记录，采用自然编码，如某一工序结束后选择预维护则将对应的基因改成维护时间。

第四层基因为记录设备故障小修，采用0-1编码。本文根据设备故障曲线，在每次加工某一工序前后计算役龄变化，对到达小修条件的设备插入小修操作表示加工某一工序中发生故障。

解码时，根据前两层编码依次得出各个工件的加工顺序和设备选择。并基于设备可靠度根据Q-learn算法得到的设备维护策略插入维护活动和维护时间，并根据小修方案插入小修活动。

4.2 种群初始化

遗传算法的初始化解的优劣直接影响着求解速度与质量，为此本文结合张国辉[21]提出的GLR初始化方案对种群初始化。GLR机器选择方法包括全局选择(GS)、局部选择(LS)和随机选择(RS)。GS和LS保证了各机器负荷平衡问题，提高机器利用率。RS使初始种群分布在整个解空间。

(1)将所有工序随机插入第一层工序编码，生成第一层基因编码，如[1 3 2 3 2 4……]得到一个初代，进而得到所有初代第一层工序编码。

(2)对已生成的工序顺序编码逐一安排机器，对所有初代的工序编码以[0.6 0.3 0.1]的概率分别使用GS、LS、RS机器选择方法。进而得到所有初代的第一、二层编码。

(3)第三层基因根据前两层基因初始化结果，由Q-learn算法选择维护方案后在相应工序后插入对应时间。

(4)第四层基因为是设备维护记录，根据维护和生产方案对每次加工工序前后故障率计算，对满足故障阈值的插入小修活动。至此，种群初始化完成。

4.3 遗传操作

遗传算法的遗传操作的选择对其性能也有着很大影响。选择操作的目的是把适应多高的个体选出作为下一代的父代，本文采取轮盘赌的方法对子代进行选择。交叉运算是遗传算法中最主要的遗传操作，是产生新个体的主要方法。文献[22]的POX交叉算子和MBM变异算子。因第三、四层基因是对在进行交叉和变异时产生的新调度方案的最佳维护方案的选择记录，不参与遗传操作。这时就需要引用修复机制，对每一次得到的方案进行维护修正。

5 算例分析

为验证本文提出基于设备健康状态和预测性维护集成模型有效性，现建立基于数控机床的评价指标体系。因现如今我国对数控机床的状态监测正处于发展阶段，目前研究主要集中对关键部件的状态检测。本文采用L公司某一生产任务涉及的的加工设备历史运行数据。L公司作为一个面向订单的多品种小批量的生产型企业，通过对其历史数据和相关人员回馈分析建立如表1对数控机床的标准属性和关键部件主轴的健康状态的评价指标体系和各特征参数组合权重。

表1 各设备评价指标数值

涉及本次生产任务的有：2台数控车床、2台数控铣床、2台加工中心、2台数控磨床共8台加工设备为研究对象。通过对各设备特征参数实测，并根据式(2)得到每个设备各个特征参数健康指数，由式(3)得出各设备运行健康指数HV1(t)分别为0.631、0.586、0.548、0.632、0.784、0.612、0.864、0.475。由式(4)得出每个设备老化健康指数HV2(t)分别为0.652、0.573、0.554、0.628、0.756、0.603、0.882、0.464。进而得到每个设备实际健康指数为0.641、0.579、0.551、0.63、0.77、0.607、0.873、0.47。根据历史数据得到各设备(表2)比例系数K、曲率系数C、形状参数β和尺度参数η。

得到设备故障率和实际役龄后，通过各设备拟合后的威布尔故障曲线和不完全维护故障率曲线对设备维护区间进行预测。根据对设备故障曲线和维护记录，本文假设设备可靠度维护区间为[0.9-0.97]，并通过Q-learn算法如图4对本次生产任务进行生产与维护集成优化。得到结果与基于阈值调度结果如图3所示，对比如表3可知。

图3 阈值维护

图4 可靠度区间维护

通过算例仿真分析结果表明提出的基于设备健康状态的可靠度区间维护与生产集成优化模型，能够很好地提高生产效率、稳定性。

6 结论

本文针对多目标柔性作业车间预维护与鲁棒性生产调度集成优化研究，提出了基于设备健康状态的可靠度区间来指导预维护与鲁棒性调度生产集成优化模型。以最小化最大完工时间最小和工序偏差度最小为优化目标，设计多目标遗传算法对模型求解。最后通过算例仿真实验，结果显示提出的模型、维护策略对生产稳定、进程、效率有效提升，验证提出模型和求解算法的可行性和有效性。