基于Bi-LSTM网络的铁路短期 货运量预测研究

郭洪鹏，刘 斌，肖 尧

(兰州交通大学 交通运输学院，甘肃 兰州 730070)

0 引言

铁路货运量预测是铁路运输企业合理规划运输资源、提高运输效率的重要手段。目前针对铁路货运量预测的研究主要是以年为单位的长期预测，采用的预测方法有多元回归预测、灰色马尔科夫模型、反向传播(Back-Propagation，BP)神经网络等[1-5]，以年为时间粒度所得结果预测精度有限，无法作为铁路日常工作计划的主要编制依据，而短期货运量(日、月货运量)预测的结果更有助于日常工作计划的编制。为了实现铁路货运物流化高质量发展，铁路运输企业需掌握短期精确的货运量预测方法，如自动回归模型、基于季节分解的时间序列模型[6-9]，以及深度学习(Deep Learning)等[10-13]。汤银英等[7]通过Holt-Winters乘法模型预测货运量，经实例验证，所得的结果高于灰色预测、回归预测等传统预测模型。谭雪等[10]通过研究结构简单且具有高效记忆功能的门控循环单元(Gated Recurrent Unit，GRU)深度网络，分别建立单步和多步预测模型进行短期货运量预测，然后将预测结果与支持向量机回归、BP神经网络和长短时记忆网络(Long Short-Term Memory，LSTM)等模型的预测结果在准确率和均方根误差指标方面比较，证明GRU深度网络的优异性。

短期货运量具有高度非线性、不确定性和序列依赖性的特征，而深度神经网络对时序数据有强大的学习能力，能较好拟合短期货运量的非线性特性。研究将双向长短时记忆网络(Bi-directional Long Short-Term Memory，Bi-LSTM)引入铁路短期货运量预测中[11]，因其具备前向计算和后向计算能力，双向LSTM的输出层不仅依赖之前的输入，还会依赖后面的数据，这样可以增加信息的交流与维持，使数据的利用更为充分。通过实际数据验证并与传统预测模型的预测结果进行比较，验证Bi-LSTM网络的预测性能和泛化性能。

1 基于Bi-LSTM网络的铁路短期货运量预测模型构建

1.1 Bi-LSTM网络理论

LSTM网络是循环神经网络(Recurrent Neural Network，RNN)的变体，改善了RNN存在的无法解决长期依赖的问题。LSTM单元结构如图1所示。其中，ct，ht分别表示模型的记忆状态和隐层状态，xt，yt分别表示模型的输入与输出，σ表示sigmoid激活函数。LSTM的单元内存在4个不同的全连接层，全连接层的每一个结点都与上一层的所有结点相连，其主要用途是把模型提取到的特征综合起来。主层是图中输出为c~t的层，其基本作用是分析当前输入xt和前一个隐状态ht-1。其他3个层是门限控制器，分别是：由ft控制的忘记门限，控制着哪些记忆状态应被丢弃；由it控制的输入门限，控制着c~t的哪些部分会被加入到记忆状态；由ot控制的输出门限，控制着哪些记忆状态应在这个时间迭代被读取和输出。随着记忆状态ct-1从左到右贯穿网络，它首先经过一个忘记门限丢弃一些记忆，然后通过输入门限选择添加一些新的记忆。因此，在每个时间迭代中，一些记忆被丢弃，同时一些记忆被增加。另外，经过额外操作，记忆状态被复制并传入tanh函数，然后其结果被输出门限过滤，从而产生新的隐状态ht。LSTM就是在这样的循环之下，学习哪些记忆需要储存，哪些记忆需要丢弃，以及从哪些记忆中去读取，从而结合输入变量去预测输出变量。

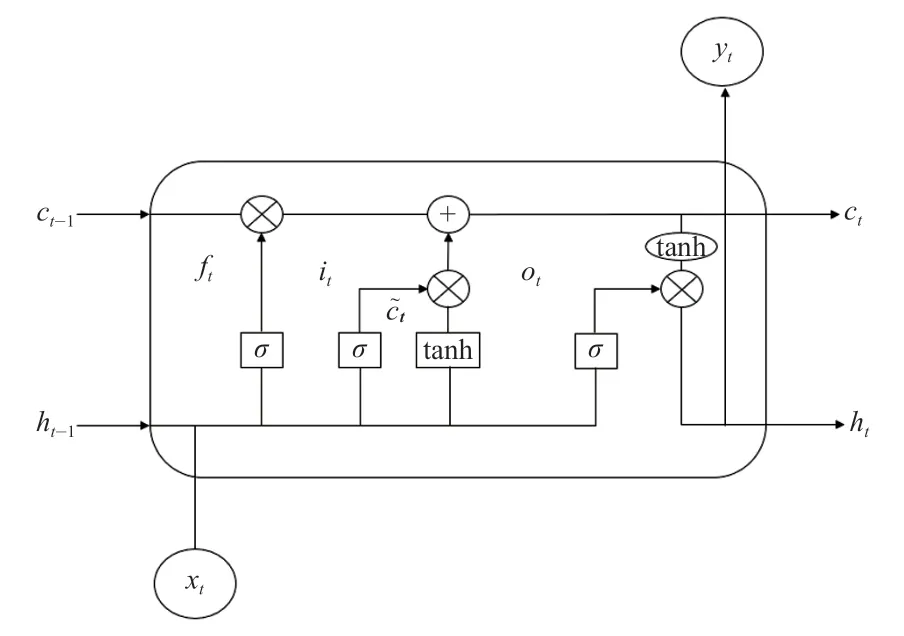
图1 LSTM单元结构Fig.1 LSTM cell structure

式中：tanh表示双曲正切激活函数；Wxc，Wxf，Wxi，Wxo表示每一层连接到输入向量xt的权重矩阵；Whc，Whf，Whi，Who表示每一层连接到前一个隐状态ht-1的权重矩阵；bc，bf，bi，bo表示每一层的偏置项。

单向LSTM网络在信息推测时采用的原理是由前向后推测信息，在单向LSTM网络基础之上，提出同时考虑前期信息和后期信息的双向长短时记忆网络——Bi-LSTM网络，可以有效保证时间序列预测所得结果的精确性[14]。

Bi-LSTM网络的计算方式分为前向计算和后向计算，水平轴表示时间序列的双方向流动，竖直轴表示信息从输入层到隐藏层和从隐藏层到输出层的单方向流动。Bi-LSTM网络结构图如图2所示。

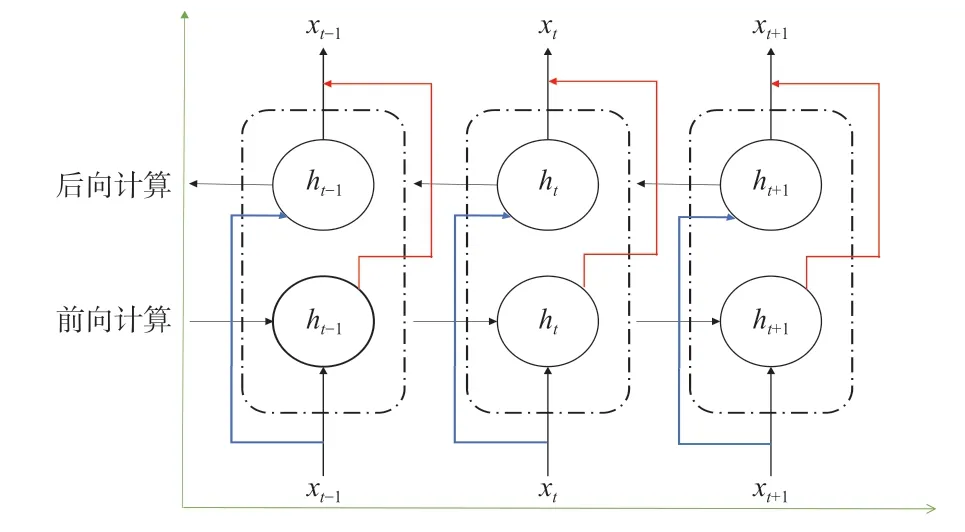
图2 Bi-LSTM网络结构图Fig.2 Diagram of Bi-LSTM network structure

另外，为了控制神经网络预测过程中出现的过拟合现象，引入Dropout方法以改善模型的适用性。该方法通过使部分神经元随机失去活性，保证所有训练都具有不同的弱分类器的性质，从而使得模型的泛化能力有所保证。

1.2 基于Bi-LSTM网络的铁路短期货运量预测模型

1.2.1 预测流程

Bi-LSTM模型预测时，假设一个样板数据时间窗步长为3，则其输入为xt-1，xt，xt+1。对于2个分离的LSTM单元，其前向计算样本按照xt-1，xt，xt+1输入，得到第一组输出状态为其后向计算样本按xt+1，xt，xt-1输入，得到另一组输出状网络计算流程图如图3所示。

图3 Bi-LSTM 网络计算流程图Fig.3 Flowchart of Bi-LSTM network calculation

由于得到的2组状态输出每个元素的特征维度是相同的，将前向计算和后项计算所得的结果进行拼接进而对于每个输入的xt，都可以得到维度为2的输出向量Yt=

1.2.2 评估指标

为评价模型预测结果的精确度以及与其他算法的预测结果进行比较，采用均方根误差RMSE、平均绝对值误差MAE和平均绝对百分比误差MAPE 3种评价指标作为模型预测精确度的评估指标以及与其他模型比较的标准，RMSE，MAE和MAPE计算公式如下。态为

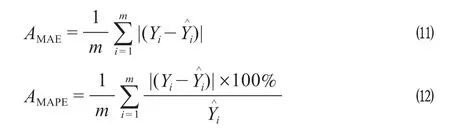
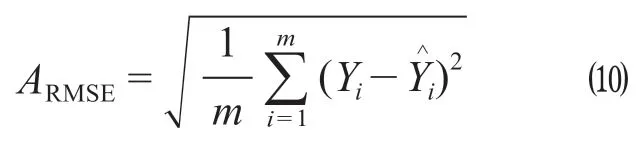
式中：ARMSE表示均方根误差；AMAE表示平均绝对值误差；AMAPE表示平均s绝对百分比误差；m表示预测结果个数；Y^

i表示真实值；Yi表示预测值。

2 实证分析

2.1 铁路短期货运量预测实验数据处理

以某铁路局集团公司为例，对铁路短期货运量进行预测。研究数据来源于2010年1月1日—2021年4月14日共4 122 d、136个月的货物发送量，某铁路局集团公司装车数如图4所示。铁路装车数是指在一定时期内铁路营业线和临时营业线上的车站承运，并填制货票以运输车运送的发送货物装车完了的车数，或者是计划期间发送货物所需要的车数。由于装车数指标在日常掌握中比货物发送吨数指标简便明确，所以在考核下达各级运输单位运输计划执行情况时，经常使用装车数作为指标，以便各单位组织车流和货流计划，因而研究采用日、月装车数作为实验数据。其中，日装车数在8 000车上下浮动，月装车数在200 000车上下浮动。由图4可以看出，某铁路局集团公司近年来货运量走势基本趋于平稳，受国家经济转型、铁路货运组织改革等宏观经济环境变化的影响，2013—2015年出现下降，在2017年开始逐渐回暖，货运量整体呈上升趋势。

机器学习中普遍的做法是将样本按7 : 3的比例从同一个样本集中随机划分出训练集和测试集。因此，将月货运量数据集分为训练集(2010年1月—2018年12月)和测试集(2019年1月—2021年3月)，日货运量数据集分为训练集(2010年1月1日—2018年12月31日)和测试集(2019年1月1日—2021年4月14日)。训练集和预测集数据分集如表1所示。

表1 训练集和预测集数据分集Tab.1 Training set and data subset of prediction set

2.2 Bi-LSTM 网络铁路短期货运量预测参数设置及实验结果

（1）参数设置。选择使用adam作为模型参数优化器，选择mse作为损失函数，并对模型中的其他超参数进行设置。超参数设置如表2所示。

表2 超参数设置Tab.2 Superparameter setting

（2）实验结果。货运量预测结果如图5所示，Bi-LSTM网络测试集评估指标如表3所示。由表3可知，基于日货运量数据的Bi-LSTM网络货运量预测结果的MAE为471，MAPE为5.30%，RMSE为616。基于月货运量数据的Bi-LSTM网络货运量预测结果的MAE为18 364，MAPE为6.92%，RMSE为20 129。一般认为MAPE在10%以内预测结果有效，2组数据的预测结果均较为精确，表明Bi-LSTM网络具有较为可观的泛化能力。

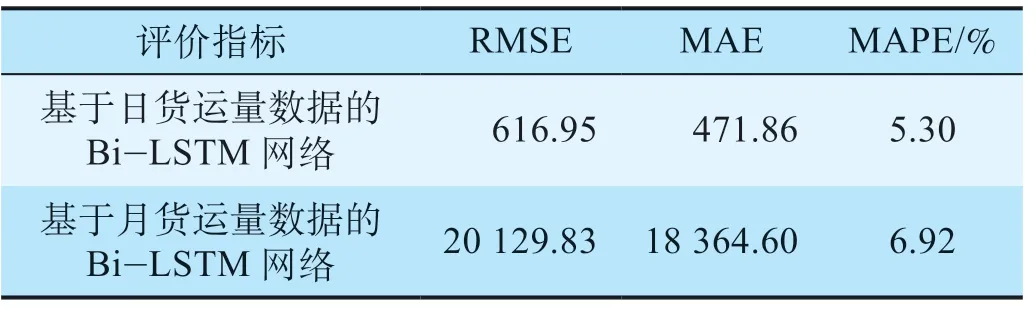
表3 Bi-LSTM网络测试集评估指标Tab.3 Evaluation indexes of Bi-LSTM network test set

图5 货运量预测结果Fig.5 Freight volume prediction

2.3 Bi-LSTM网络铁路短期货运量预测比较算法

（1）随机森林(Random Forest，RF)。作为bagging法中的特殊情况，随机森林将决策树用作bagging中的模型，以保证更准确地找到最优解。主要原理如下：①用bootstrap法生成m个训练集。②针对所有的训练集，构造对应每一个训练集的决策树。在节点搜索特征进行分裂时，并不是对所有特征进行搜索而使得指标最大，而是在特征中随机抽取一部分特征，在抽到的特征中找到最优解，应用于节点，进行分裂。正是因为bagging的存在，随机森林法实际上相当于对所有样本和每一个特征都进行采样，以此实现避免过拟合的目的。

（2）支持向量机(Support Vector Machines，SVM)。作为二分类模型中的一种特殊类型，SVM使结构的复杂性得到有效的降低，保证在解决样本数量少、线性、非线性及高维模式识别中呈现出诸多独有的优势[15]。这一特点还能在函数拟合等各类机器学习问题中得到推广和应用。由于SVM以统计学习理论中的VC理论和结构风险最小原理为建立依据，因而在泛化能力上有明显的提高。通过对数据维度的提升，以保证做回归时可以实现高维空间构造线性函数并实现线性回归。

（3）极端梯度提升(eXtreme Gradient Boosting，XGBoost)。由 于XGBoost具有显著的预测精确度而得到广泛的应用。XGBoost的本质是梯度增强决策树(Gradient Boosting Decision Tree，GBDT)算法的改进。因此，XGBoost既可以用于分类也可以用于回归问题中，具有计算速度快、模型表现好的特点。

（4）LSTM网络。在以往的时间序列预测中，RNN已经得到广泛的运用，但数据随着时间序列的不断增加，梯度爆炸和消失的问题也随之而来。LSTM网络就是为解决梯度爆炸和消失这一弊端专门设计的一种特殊类型的RNN。

2.4 Bi-LSTM 网络铁路短期货运量预测比较算法实验结果

为验证Bi-LSTM网络预测结果的精确度，同样采用Bi-LSTM网络的数据分集和参数设置，分别使用RF，SVM，XGBoost和LSTM 4种机器学习算法对日装车数及月装车数进行预测。

（1）预测结果评估指标比较。5种模型预测结果评估指标比较如表4所示。通过分析比较表4中的数据可知，Bi-LSTM网络的日、月货运量预测结果，较RF而言在日货运量预测结果MAPE低1.34%、月货运量预测结果MAPE低2.93%，较SVM而言在日货运量预测结果MAPE低4.6%、月货运量预测结果MAPE低4.89%，其RMSE有较为明显的降低，说明Bi-LSTM网络预测性具有较为明显的优势。与XGBoost模型相比，在日货运量预测上，平均绝对百分比误差比较接近，但在月货运量预测上Bi-LSTM网络误差更低。与LSTM网络相比，两者预测误差较为接近，但Bi-LSTM网络采用双向计算的原理，同时考虑前后期信息，使得预测结果更为精确。

表4 5种模型预测结果评估指标比较Tab.4 Comparison of evaluation indexes of prediction by five models

（2）月货运量预测比较。5种模型月货运量预测比较如图6所示。从图6可以看出Bi-LSTM网络和LSTM网络在趋势上与实际月货运量最为接近，但Bi-LSTM网络在2020年5月开始具有和实际货运量相同的上升趋势，说明Bi-LSTM网络具有更高的预测精度，模型在泛化能力上具有更好的表现。

图6 5种模型月货运量预测比较Fig.6 Comparison of monthly freight volume prediction by five models

（3）日货运量预测比较。以实际日货运量为横坐标、预测值为纵坐标建立5种模型日货运量预测效果散点图，5种模型日货运量预测效果如图7所示。通过观察斜率和散点密集度可以发现，Bi-LSTM网络的预测结果斜率更接近1且更密集，说明Bi-LSTM网络的预测结果精确度更高。

图7 5种模型日货运量预测效果Fig.7 Daily freight volume prediction by five models

3 结束语

短期货运量预测研究是铁路运输企业编制日常工作计划的重要依据，准确的货运量预测结果对铁路货运组织工作具有积极意义。研究结合实际情况，建立基于Bi-LSTM网络的铁路短期货运量预测模型，并与RF，SVM，XGBoost和LSTM 4种模型进行比较，验证Bi-LSTM网络的预测精确度和泛化能力均高于其他4种模型，为铁路短期货运量预测提供一种新的思路。在接下来的研究中，还可以改进Bi-LSTM模型，以进一步提高模型的预测精度。