云环境中细粒度的数据安全共享方案
文鹏程,沈济南†,梁 芳,许振武,胡俊鹏,
1.湖北民族大学 信息工程学院,湖北 恩施 445000;
2.四川大学 网络空间安全学院,四川 成都 610207
0 引言
云计算技术受到越来越多用户的青睐,其主要原因是该技术的弹性计算、海量存储、便捷访问等优点。由于用户以及用户数据爆发性地增长,系统面临着崩溃和被黑客攻击的危险[1]。此外,数据安全成为了云服务发展的瓶颈,面对这一亟须解决的问题,学者们提出了多种多样的解决方法。Bell等[2]提出强制访问模型(mandatory access control,MAC)的概念,所有资源都由系统控制并受MAC策略的约束。要访问基于MAC的系统中的资源,主体必须持有该资源所需的适当安全许可及其安全分类。自主访问控制模型(discretionary access control,DAC)的访问控制策略可以看成一个矩阵,通过该访问控制矩阵实现对请求合法性的判定[3],客体的所有者负责管理该客体的访问授权,有权分配、更改该客体的属性信息。Galindo引入了一种基于身份的加密(identity-based encryption,IBE)方案,其中发送方可以使用接收方的身份作为加密消息的公钥[4]。Xu等[5]和Shen等[6]分别提出了一种改进的代理重加密算法(proxy re-encryption,PRE),通过减少双线性运算提高系统的运行效率。Oh等[7]提出基于角色的访问控制(role based access control,RBAC)的方案,融入了自下而上的权限角色管理方法。Goyal等[8]提出基于属性加密(attri⁃bute-based encryption,ABE)的方案,密文被标记为一组属性,私有密钥与控制用户能够解密哪些密文的访问结构相关联。后续全同态加密算法(fully ho⁃momorphic encryption,FHE)[9,10]和密文搜索算法等也相继提出。
上述方案或模型面临一个问题,就是当用户数据访问策略发生改变时,必须由用户对数据进行重新加密,并需要将加密后的文件重新上传云端,这势必产生不可忽略的计算和通信开销。直至目前,有大量的研究对访问模型中策略变化和策略更新进行了探索[11,12],并且所提出的方案将重加密过程中所需要优质的网络资源和计算资源转移给专用代理(云服务器)。虽然之前的部分研究降低了用户物理机的性能需求,使用户得到了极大的便利,但是并未很好地降低第三方云服务器所需要的性能需求。
针对以上问题,本文提出了优化的、低成本的、安全的细粒度数据共享方案,通过降低重加密阶段的计算复杂度极大限度地降低了第三方云服务器的性能需求,主要创新点为:
1)针对多权限云中的数据,提出灵活、安全的访问控制模型,即使云服务提供商不可信,也能保证数据安全;
2)将基于改进的代理重加密技术与改进的基于属性加密技术相结合,减少双线性运算次数,提高系统的运行效率,降低了云服务器的计算资源;
3)制定高效的策略更新方案,降低计算开销。
1 相关理论知识
本节针对改进方案中涉及的基本理论知识进行了描述,包含双线性映射、Fisher-Yates scram⁃bling算法以及基于属性的加密。其中,Fisher-Yates scrambling算法为随机置乱算法,在方案中可以对加密后的密文进行再次随机置乱,以确保方案的安全性。
1.1 双线性映射
定义1(双线性映射[5,6]):当映射函数e:G1×G2→G T满足以下条件时,称之为双线性映射:
1)G1,G2,GT是q阶的群,其中q是素数;
3)非退化性,即如果g是G1的成员,那么e(g,g)是GT的成员;
4)e是可计算的,对于所有的p,q∈G1,存在有效算法,可以计算出e(p,q)。
1.2 Fisher-Yates scrambling算法
定义2(Fisher-Yates scrambling[13]):Fisher-Yates随机置乱算法也称为Knuth算法,是一种经典的shuffle算法。该算法的本质是生成随机排列的有限集。这个算法是无偏的,总数为n!,每种排列都有相同的概率。该算法效率很高,时间复杂度为O(n),不需要额外的存储空间。对于序列A[n],执行以下步骤:
1)令0 2)生成一个随机整数j(1 3)交换A i和A j的值,且i=i-1; 4)重复2),3),直到i=1时停止重复。 对于执行Fisher-Yates scrambling算法之后的数组,我们定义为:A{j,n}⇌ϑ{j,n}。 基于密文策略的属性加密(ciphertext-policy ABE,CP-ABE),Bethencourt,Sahai和Waters提供了一种加密方案[14],该方案基于属性的加密工作,能够将复杂的基于树的访问策略嵌入到密文中,比基于密钥策略的属性加密(key-policy ABE,KPABE)性能更好。CP-ABE还引入了“变量属性”,它使用一组传统属性来表示可以通过更复杂的操作(包括>,<,<>和=)进行评估的值。通过以下步骤完成:对于介于0和某个系统定义的最大值之间的给定十进制整数,首先将值转换为二进制,然后为每个位创建一个属性。例如,可以使用“access_level_flexint_1xxx OR(access_level_flex⁃int_x1xx AND(access_level_flexint_xx1x OR ac⁃cess_level_flexint_xxx1))”策略来强制执行“>5”,该策略将创建访问树。 本节阐述所提出方案中的细粒度访问策略设计,其中包含方案流程、算法设计,详细描述了细粒度访问策略模块设计、核心算法的执行流程。 本文提出的基于改进的代理重加密与属性加密结合的访问策略(ACSBPA)方案由初始化算法SetupPRE-ABE(),密钥生成算法ExtractPRE-ABE(),初始加密算法EncPRE-ABE(),重加密密钥生成算法RKExtractPRE-ABE(),代理重加密算法ReEncPRE-ABE(),初始密文解密算法Dec1PRE-ABE()和重加密密文解密算法Dec2PRE-ABE())七个算法组成。 如图1所示,方案的主要组成部分实体部分有:属性管理机构(attribute management agency,AMA),密 钥 生 成 中 心(key generation center,KGC),数据拥有者(data owner,DO),数据请求者(data recipient,DR)以及云服务提供商(cloud ser⁃vice provider,CSP)。 图1 云环境下细粒度访问策略方案Fig.1 Fine-grained access strategy in the cloud 方案中各实体之间的交互描述如下。 1)数据拥有者与属性管理机构交互:在属性管理机构中记录了数据拥有者的属性值,在初次加密时,数据拥有者可以设置访问策略来限制访问加密文件的权限,同时数据拥有者的属性值也限制了其访问数据的权限以及范围;当用户为数据请求者时也需要与属性管理机构交互,完成用户数据请求者的属性注册。属性管理机构存储了数据拥有者、数据请求者的属性值,当访问策略需要更新时,数据拥有者从属性管理机构获取数据接收者的属性值,更新访问策略,对明文执行加密或重加密操作。 2)属性管理机构与密钥生成中心交互:属性管理机构将用户初始的属性值、变化后的属性发送到密钥生成中心,密钥生成中心根据用户未更改和已更改的属性为用户生成最新的基于属性的密钥、传统的公私密钥对、对称加密密钥。 3)密钥生成中心与数据请求者交互:数据请求者根据数据不同的存储方式向密钥生成中心请求密钥,若需要存储于云端,则密钥生成中心发送给数据拥有者加密数据所需要的所有私钥。 4)数据拥有者和云服务提供商交互:数据拥有者制定基于CP-ABE的密文访问控制策略,使用获得的密钥、参数、访问策略对数据加密并上传至云端。在此阶段,密文采取树结构访问控制策略,用户的密钥与属性集有关,只有当用户满足访问控制策略才能解密密文。 5)数据请求者与云服务提供商交互:数据请求者申请访问数据,只有符合访问策略则可以将初次加密后的密文转换为明文。交互至此,在执行完1),2),3),4),5)后,完成了密文初次共享。 6)密钥生成中心与云服务提供商交互:密钥生成中心将重加密密钥发送到云服务提供商端,云服务提供商使用基于数据拥有者和数据请求者生成的重加密密钥对初次加密的密文重加密,最后将重加密密文存储于云服务提供商。 7)数据请求者与数据拥有者交互:若数据请求者属于数据拥有者指定的新的属性集,则数据拥有者通过秘密通道将基于属性的私钥发送到数据请求者端;若数据请求者不属于数据拥有者指定的新的属性集,则无法获取基于属性的私钥及重加密后的密文。 8)数据请求者与云服务提供商交互:数据请求者从CSP端获取密文,使用由数据拥有者通过秘密通道发送的基于属性的密钥、自身的传统的公私密钥对、系统参数、重加密密文作为解密条件,将密文转换为明文。交互到此阶段,在执行完1)、2)、3)、4)、6)、7)、8)后完成了密文的重加密共享。 在本方案中,由发送方制定访问控制策略。密文采取树结构访问控制策略,数据访问者密钥与属性集有关,只有当数据访问者满足访问控制策略才能解密密文,执行流程如下: 1)初始化:密钥生成中心执行SetupPRE-ABE()和ExtractPRE-ABE(),并且与属性管理机构交互。由属性管理机构将指定密文接收者属性集合标记为attr1,根据attr1生成传统的公私钥对。同时,由密钥生成中心生成基于AES算法的对称密钥,完成整个系统初始化。 2)初次密文加密/上传:由属性管理机构根据attr1,生成访问策略policy。之后,执行EncPRE-ABE(),将明文加密为密文。最后,将初始密文发送给云端,由云端对密文存储并由云端执行重加密算法。 3)初次密文下载/解密:当符合attr1的用户申请访问数据时,从云端下载密文数据后,使用Dec1PRE-ABE()解成明文。 4)密文共享:若数据拥有者欲将此数据分享给属于attr1中的用户,将密文上传至云端,属于attr1中的用户直接从云端下载密文,用其私钥SKABEPRE解密密文。反之,若合法数据接收者不属于attr1,则创建新的属性集attr2,更新访问策略。若执行代理重加密共享时,由属性管理机构与数据拥有者以及密钥生成中心交互,执行重加密密钥生成算法,生成一个重加密密钥,由云端或第三方代理服务器执行重加密算法。在重加密时,通过执行重加密算法将数据分享给属于attr2的用户。云端执行代理重加密算法时,计算并输出重加密密文。 5)重加密密文下载/解密:当属于attr2集中的数据请求者申请数据时,若该数据请求者符合传统公私钥对的解密算法,则云服务器将与数据拥有者通信,数据拥有者也会与KGC和AMA确认数据请求者的属性以及属性公钥是否符合attr2。数据拥有者确认授权后,通过安全通道将发送给数据请求者,数据请求者从云端下载重加密密文,执行解密算法,将重加密密文解密为明文。 1)初始化SetupPRE-ABE(λ) 构造双线性映射e:G1×G2→GT,其中,G1、G2和GT是q阶的椭圆曲线群,q是素数。随机选择两个哈希函数H1:{0,1}*→ℤ*p,H2:GT→G,H1可以将任意长度的0/1串全部映射到ℤ*q中,H2可以将GT中的元全部映射到G1,G2中。KGC输出系统公共参数paramsPRE-ABE,paramsPRE-ABE是系统中所有用户加密和解密所需要的参数。此外,生成主秘密参数MKPRE-ABE,MKPRE-ABE由KGC保留,为用户生成解密所需的私钥。 其中:g1是G1的生成元,g2是G2的生成元,α和 2)密钥生成ExtractPRE-ABE() KGC根据数据拥有者和用户DR的属性集生成传统的公私密钥对,其中 以 MKPRE-ABE、用 户 属 性 集 attr1以 及paramsPRE-ABE作为输入,将属性密钥分发给用户SKABEPRE(attr1,D j)。执行操作如下 以paramsPRE-ABE、基于AES加密的对称密钥明文数据信息M以及访问策略po作为输入,取s∈GT,利用Fisher-Yates scrambling算法将经过哈希变换后的s与基于AES加密的对称密钥随机置乱为℘,再将s与℘随机置乱,输出初始密文ci(ci1,ci2,ci3),其中 秦铁崖满不在乎:“管他是大神还是小妖,是八只老虎还是八只乌龟,既然敢给江云飞下战书,想必有两下子,他敢挑战,我就敢收拾他。” 本节从方案的一致性和安全性全面分析了方案中的核心算法,证明了本方案的可行性、合理性以及保密性。 定理1任何通过正确步骤生成的代理重加密密文都可由指定属性集的接收者解密。 可得出最后的明文。 定义3判定双线性Diffie-Hellman难题: G和GT两个q(q是素数)阶的椭圆曲线,g是G的一个随机生成元。在双线性映射e:G×G→GT中的DBDH(Decisional Bilinear Diffie-Hellman)难题 被 定 义 为 攻 击 者A区分(g a,g b,g c,e(g,g)abc)和(g a,g b,g c,e(g,g)r)两个元组的优势,其中a,b,c,r都是在中随机选取的,且用代表上述优势,如果对于任何多项式时间的攻击都是可忽略的,就可以说DBDH成立。 定义4IND-sABE-CPA攻击游戏 定理2ACSBPA方案中DBDH难题成立,所以方案在随机预言机模型下具有IND-sABECPA安全性。 证 1)初始化:攻击者A首先选择一个属性集合作为挑战的属性集合attr1*,同时攻击者A将s*和γ*作为挑战条件;然后将attr1*和s*发送给攻击者B;最后攻击者B将att r1*、s*和γ*发送给挑战者C。 2)设置:挑战者C执行SetupPRE-ABE(λ)算法为攻击者生成ACSBPA中的主公共参数paramsPRE-ABE和 主 秘 密 参 数MKPRE-ABE=(w,β)。在ACSBPA方案所有执行过程中,由于哈希函数H在安全性证明中被认为是随机预言机,所以其不会被发送。挑战者C将paramsPRE-ABE发送给攻击者B,攻击者B得到哈希函数查询QHPRE-ABE(attr1),挑战者C将查询到的用户属性与相对应的哈希值记录在表L H2中。 4)挑战阶段:首次查询是否结束由攻击者A决定,并由攻击者A向攻击者B发送两条挑战明文(m0,m1),攻击者B直接将挑战明文(m0,m1)发送给挑战者C;挑战者C执行EncABE(paramsPRE-ABE,attr1*,mb)生 成 密文来进行挑战(其中b是在{0,1}中是随机的);最后将密文发送给攻击者B。此时,根据密文 5)二次查询阶段:此阶段与首次查询阶段相同。 6)猜测阶段:攻击者A猜测出一个结果b′∈{0,1},攻击者B将其发送给挑战者C,如果b′=b,则攻击者A获得了这场游戏的胜利。最后,获得这场游戏胜利的优势表示为 如果攻击者A成为了ACSBPA方案中INDsABE-CPA的获胜者,则攻击者B成功攻破ACSBPA方案IND-sABE-CPA的安全性。 综上,ACSBPA具有DBDH难题的难解性和IND-sABE-CPA安全性。 定理3ACSBPA方案中初次加密阶段符合Fisher-Yates scrambling随机置乱算法,所以该方案在初次加密阶段生成的密文更具有随机性,密文更具有难解性。 证 1)从1~n之间随机选出一个数和最后一个数(n)交换,然后从1~n-1之间随机选出一个数和倒数第二个数(n-1)交换。假设有5个数:0,1,2,3,4。 第一步,从[0,4]这5个位置中(包含0和4)随机出一个数(比如是3)和4号交换,得到0,1,2,4,3。原来4的位置放3的概率就是1/5。 第二步,从[0,3]这4个位置中(包含0和3)随机出一个数(比如是0)和3号交换,得到4,1,2,0,3。原来3的位置放0的概率就是(4/5)·(1/4)=1/5。 第三步,从[0,2]这3个位置中(包含0和2)随机出一个数(比如是0)和2号交换,得到2,1,4,0,3。原来2的位置放4的概率就是(4/5)·(3/4)·(1/3)=1/5。 第四步,从[0,1]这2个位置中(包含0和1)随机出一个数(比如是0)和1号交换,得到1,2,4,0,3。原来1的位置放2的概率就是(4/5)·(3/4)·(2/3)·(1/2)=1/5。 第五步,从[0,0]这1个位置中(包含0和0)随机出一个数(比如是0)和0号交换,得到1,2,4,0,3。原来0的位置放1的概率就是(4/5)·(3/4)·(2/3)·(1/2)=1/5。 2)在 加 密 计 算 中,s∈GT,利 用Fisher-Yates scrambling算法将经过哈希变换后的s与随机置乱为℘,再将s与℘随机置乱,确保密文和明文的安全性。在不增加方案的计算消耗和存储空间的情况下,ACSBPA方案中初次加密阶段符合Fisher-Yates scrambling随机置乱算法。 本文提出的ACSBPA方案与苏铓等[15]提出的基于代理重加密的云数据访问授权确定性更新方案(PAUA)的时间复杂性的对比如表1。其中,te代表指数运算,tl代表线性对运算。 表1 ACSBPA与PAUA复杂性对比分析Table 1 Comparative analysis of ACSBPA and PAUA complexity 文献[15]是近期提出的代理重加密与属性加密机制方案。从表1可以看出,本文提出的ACSBPA方案在复杂性方面优于PAUA方案。 本次实验仿真是在AMD R7 4800H CPU@2.90 GHz,32 GB内存,操作系统为Windows 10,Myeclipse 2014版PC上进行的。在本节中,将策略更新函数,初次加密算法,重加密算法,重解密算法与近几年相关文献进行对比分析。 1)策略更新函数po=(k,attr1,cl) ACSBPA方案通过“不同的属性数量”来对性能进行评估。在仿真测试中,访问策略包含40个属性,所加密的文件为1 GB。包含“or”,“and”和“kofn”门限。本次测试通过改变访问策略中的属性数量来测量策略更新的处理时间。如图2所示,本文策略更新时间保持在3~5 ms,解密所需时间没有随策略的增加呈正比例增长。而在属性为40个时,文献[16,17]策略更新时解密所需时间超过了300 ms。 图2 策略更新开销Fig.2 The cost of policy update 2)初次加密算法 如图3所示,在属性为5个和40个时,本方案初次加密算法计算耗时分别为33 ms和240 ms,文献[18]初次加密计算耗时分别为29 ms和190 ms,文献[19]初次加密算法计算耗时分别为26 ms和189 ms。三种方案初次加密算法计算耗时随着属性数量的增加呈正比例增长。虽然本文方案中的初次加密算法计算耗时高于文献[18,19],但是这个计算耗时在客户的正常接受范围内。 图3 初次加密计算开销Fig.3 The calculation cost of initial encryption 3)重加密算法 本文方案中的重加密算法不涉及双线性映射,对第三方云服务器所需的性能需求达到最大限度的优化。在用户数量极速增长的情况下,第三方云服务器所需要的性能相对较小。如表2所示,属性为5~40个时,重加密算法的计算耗时在50 ms以内,而文献[20]方案中的重加密计算耗时随着属性数量的增加呈正比例增长。当属性为40个时,计算耗时达到了1 850 ms。由此说明,本方案在重加密方面计算开销更小。 表2 重加密计算开销Table 2 The calculation cost of re-encryption ms 4)解密算法 如图4所示,虽然属性在不断地增加,但是本文解密算法的计算耗时保持在26~28 ms,而文献[19]和[21]方案中的解密计算耗时随着属性数量的增加而增加明显。当属性增加到40个时,文献[19,21]提出方案的计算耗时都超过了250 ms。因此,与文献[19,21]相比,本文解密算法的计算开销具有明显的优势。 图4 解密计算开销Fig.4 The calculation cost of decryption 随着云服务的爆发性发展,用户的数据安全成为研究的焦点。代理重加密和基于属性加密成为研究者的关注点之一。本文以不完全可信的云服务商为背景,改进代理重加密算法,实现了云中数据的安全存储以及密文共享,且降低了云平台所需的性能需求。同时,在明文初次加密阶段使用Fisher-Yatesscrambling算法将密钥与加密元素两次置乱,在不增加方案的计算开销的情况下,增加了封装对称密钥的随机性和封装后密文的难解性。另外,结合基于属性加密算法,实现了多用户多属性的访问策略,解密时间与用户属性没有形成正比关系。本方案保证了云环境中用户数据的安全,还实现了数据的安全共享。1.3 基于属性加密
2 细粒度访问策略设计
2.1 方案流程

2.2 算法设计


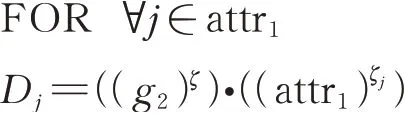



3 方案安全性及证明
3.1 方案的一致性

3.2 方案的安全性


4 实验及性能分析
4.1 复杂性对比

4.2 仿真及计算开销分析




5 结语

