多弹分布式时间协同非奇异制导方法
杨小艳 张金鹏 马慧敏 宋申民



摘 要:针对多枚导弹协同攻击地面静止目标问题,提出一种非奇异分布式协同末制导律。 通过选取预估攻击时间作为一致性变量,将一致性算法与非奇异制导律相结合,避免了小角度假设和指定攻击时间所带来的局限性。 基于李雅普诺夫稳定性理论对系统的一致性误差以及前置角给出闭环稳定性证明,从而证明所提出分布式协同制导律的有效性。 仿真对比分析进一步验证了所提制导律在大初始前置角下的脱靶量相比于所对比的分布式制导律小了一个量级,说明了制导性能的有效性和优越性。
关键词:分布式;协同制导;非奇异;无小角度假设;一致性算法;有限时间; 导弹
中图分类号:TJ765.3;V249.1 文献标识码: A 文章编号:1673-5048(2022)01-0035-06[SQ0]
0 引 言
现今,隨着防御系统,如近程防御武器系统的增强,单枚导弹突破敌方防御系统并以较高的精度击中目标越来越难以实现[1]。 此外,随着体系概念的提出,通过多弹攻击时间协同可以实现对目标的饱和攻击[2],因此,设计满足攻击时间约束的制导律具有较高的实际意义。
现有文献研究中,满足攻击时间约束的协同攻击可以大致分为两个方面,即单个攻击和协同攻击。 其中,协同攻击是通过多枚导弹之间相互通信并进行信息交流实现的。 而对于单个攻击而言,每枚导弹的攻击时间是提前指定的,且一般在群体中的最大初始预估飞行时间以及最小初始预估飞行时间之间取值。 在指定攻击时间制导律设计方面,主要包括比例制导律加偏置项[3-4]、滑模控制[5-8]、基于李雅普诺夫攻击时间制导律[9-10]等。 文献[3]将以比例制导律作为控制器所得到的预估攻击时间与指定攻击时间的差值作为反馈控制量,从而实现多弹在攻击时间上的协同。 受限于线性制导模型,文献[4]设计了非线性制导模型下的比例偏置时间约束制导律,并推导了比例制导下具有一般性的剩余飞行时间估计式。 文献[5]基于滑模面设计了针对指定攻击时间非线性模型的时间约束制导律,通过在等效控制量的基础上引入两个鲁棒控制量,可以有效避免奇异现象以及半负定问题的产生。 文献[6]提出一个新型的滑模面,通过将滑模面设计为攻击时间误差以及视线角速率的函数,可以保证对目标的协同攻击。 上述文献针对指定攻击时间的协同制导律设计,需要以预估剩余飞行时间代替剩余飞行时间,由于文献[4]中的预估飞行时间是基于小角度假设推导的,从而限制了其适用性。 文献[7]提出基于滑模的无预估剩余飞行时间估计的协同制导律,通过设计非负权重来保证相对距离收敛到0,剩余时间收敛到期望剩余飞行时间。 文献[9-10]提出基于李雅普诺夫的攻击时间协同制导律,其中,文献[10]推导了以贝塔函数表示的期望攻击时间的闭环解,且通过调节控制参数可以满足攻击时间约束。 然而,对于个体攻击而言,如何合理选取指定攻击时间从而保证多弹成功协同击中目标具有很大的挑战性。
对于协同攻击,多弹间通过信息交流完成时间协同可以看作是解决指定攻击时间不合理问题的一种有效方法, 且一致性算法可以实现多弹之间的信息交互。 通过选择一个合理的协调变量,如预估剩余飞行时间或预估剩余飞行距离,多弹可以通过一致性协调变量,实现对目标的协同攻击。 文献[11]提出一种协同比例偏置制导律, 在比例制导的基础上引入一个时变导航比。 但由于采用集中式通信架构,增加了通信负担,并且会降低制导律的可靠性。 基于几何制导策略的优越性,文献[12]提出最大一致性的协同制导策略,但其仅适用于领弹-从弹制导架构,且在攻击末端导弹的加速度并不能收敛到0,并随着从弹的数量增加,加速度增大。 文献[13]以剩余相对距离作为从弹与领弹间的信息交流。 文献[14]基于二阶多智能体一致性协议提出一种分布式协同制导律,不同于传统的攻击模型,其是建立在弹体系下的动力学方程,通过反馈线性化,设计出对标称距离及标称速度进行协同的比例偏置制导律。 然而,其不能应用于大前置角的攻击场景,且是一个开环系统,缺少稳定性证明。 文献[15]提出基于有限时间一致性和滑模面的协同攻击制导律。 文献[16]基于两种不同形式的预估剩余飞行时间表达式,提出两种基于比例制导的分布式协同制导律。 通过引入时变导航比,当一致性误差收敛到0时,制导律切换为比例制导律,实现对目标的协同攻击。 然而,该方法在设计制导律时,考虑了轴向可控的情形,而这并不适用于无动力的导弹制导律设计问题。 文献[17]在文献[16]的基础上仅设计了法向制导律,但由于在推导过程中存在小角度假设,因此仿真场景受到限制。
综上所述,针对现有时间协同制导律,指定时间协同制导时,多弹间不同的初始条件下,攻击时间的合理选取仍是现今需要解决的问题。 基于信息交流的时间协同制导,当以领从式架构进行通信时,会增加通信负担。 基于比例偏置的分布式架构的协同制导可以有效解决集中式架构所带来的局限性,但现有文献中针对比例偏置的协同制导律存在开环控制或小角度假设,使得所设计的协同制导律缺少闭环稳定性证明,或大初始前置角下制导性能降低。 针对上述问题,本文考虑了针对静止目标的基于非线性动力学模型的二维多弹时间协同制导律设计问题,在文献[5,16]的启发下,通过将一致性理论和非奇异制导律相结合设计了无小角度假设的分布式多弹协同制导律。 选取预估飞行时间作为一致性变量,非奇异等效控制量使得预估攻击时间动力学满足有限时间一致性协议形式,鲁棒控制量则实现一致性误差以及前置角均趋于0,即多弹对目标的协同攻击。
3 仿真校验
为了对所提出的非奇异分布式协同制导律的有效性进行验证,进行对比仿真分析,且设置仿真场景为3枚导弹攻击静止目标。 对比实验选择文献[16]中的分布式协同制导律思想,考虑到其含有轴向控制力,而文献[17]的第3章在文献[16]的基础上略去了轴向控制力对速度的调节,并仍采取分布式协同制导律设计思想,因此以文献[17]作为对比实验,其控制器设计如下:
ami=NaiVmiq·mi
Nai=N{1-k1isgn[∑nj=1aij(t^goj-t^goi)]μ-
k2i∑nj=1aij(t^goj-t^goi)}(34)
其通信拓撲图如图2所示。 目标位置设置为(0 m, 0 m),即位于惯性坐标系的原点。 表1所示为3枚导弹的初始参数。 考虑到导弹执行器的物理限制,设定其最大法向过载为±30g, g为重力加速度,g=9.8 m/s2。 在下面的仿真中均设置导航比N=3。
设置仿真步长为0.01,控制器参数为k0=k1=k2=200,p=1.3,μ=0.9。 式(27)中的控制器参数设置为k1=10, k2=5,N=3,μ=0.8。 并简记式(7)~(9)为控制器1,记式(21)为控制器2。
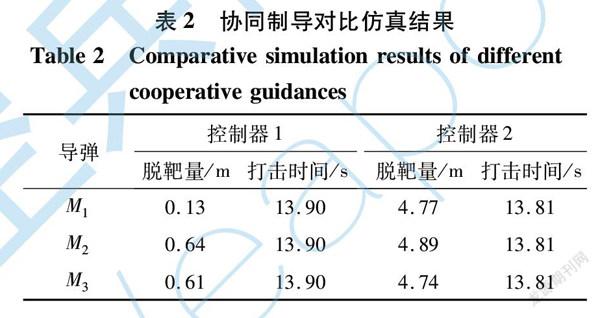
相关的仿真结果如图3~ 5以及表2所示。 由图3(a)可知,3枚导弹的预估攻击时间在5 s左右趋于一致。
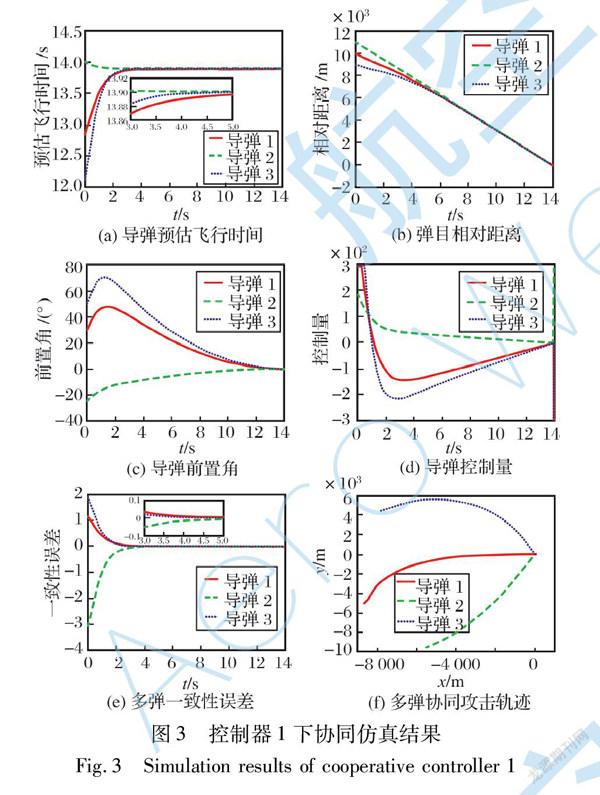
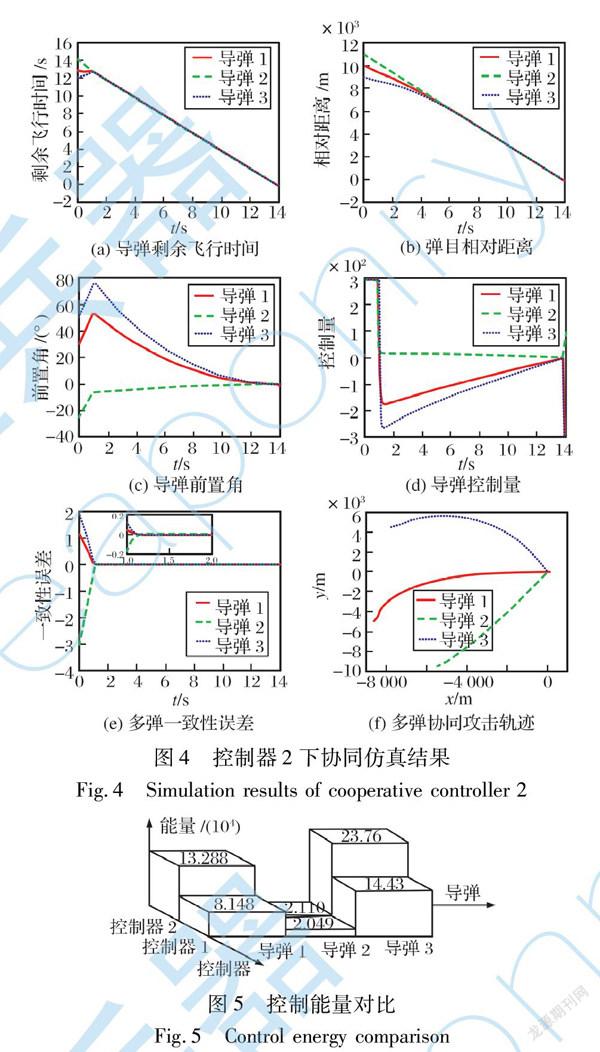
由图3(c)可知,大初始前置角下3枚导弹的前置角最终均趋于0,从而保证对目标的攻击。 由图3(d)可知,导弹1和导弹3初始控制量饱和,这是由于导弹1和导弹3的初始前置角较大导致的。 在多弹对目标协同打击时刻之后,3枚导弹的控制量均出现奇异,这是由于当每枚导弹击中目标之后会出现rmi=0的情况。 通过与图4(d)中控制器2下的控制量进行对比分析可知,相比于控制器2,控制器1在整个末制导过程中控制量更小,且由图5可知,控制器1作用下的每枚导弹的控制能量均小于控制器2作用下的控制能量,从而说明了控制器1的控制性能较优。
由图3(e)和图4(e)可知,控制器1下多弹的一致性误差为10-3,控制器2下的多弹一致性误差为10-4。 说明控制器2在提高一致性误差时降低了控制性能,而对于多弹协同攻击问题,相比于时间协同,对目标的精确打击会更重要。 由图3(f)和图4(f)可知,在控制器1以及控制器2的作用下均能实现对目标的多弹协同打击。
由表2可知,在大初始前置角下,控制器1下每枚导弹的脱靶量较小,从而说明了在大初始前置角下控制器1的命中精度更高。
4 结 论
本文针对多弹协同攻击地面静止目标问题,提出一种非奇异分布式协同制导律。 不同于现有分布式比例偏置协同制导,本文在协同制导律设计时未采用小角度假设,且通过将非奇异制导律与一致性理论相结合,可以有效解决指定攻击时间以及集中式协同架构所带来的局
限性。 但在设计分布式协同制导律时,未考虑攻击角约束,而现有协同制导律设计中,满足攻击时间和攻击角约束,可以实现对敌方目标重点部分进行饱和精确打击。 因此,下一阶段是设计满足攻击角约束的分布式时间协同制导律。
参考文献:
[1] 赵建博, 杨树兴. 多导弹协同制导研究综述[J]. 航空学报, 2017, 38(1): 020256.
Zhao Jianbo, Yang Shuxing. Review of Multi-Missile Cooperative Guidance[J]. Acta Aeronautica et Astronautica Sinica, 2017, 38(1): 020256.(in Chinese)
[2] 宋俊红. 拦截机动目标的有限时间制导律及多弹协同制导律研究[D]. 哈尔滨: 哈尔滨工业大学, 2018.
Song Junhong. Research on Finite-Time Guidance Law and Coopera-tive Guidance Law of Multi-Missiles for Intercepting Maneuvering Target[D]. Harbin: Harbin Institute of Technology, 2018. (in Chinese)
[3] Jeon I S, Lee J I, Tahk M J. Impact-Time-Control Guidance Law for Anti-Ship Missiles[J]. IEEE Transactions on Control Systems Technology, 2006, 14(2): 260-266.
[4] Jeon I S, Lee J I, Tahk M J. Impact-Time-Control Guidance with Generalized Proportional Navigation Based on Nonlinear Formulation[J]. Journal of Guidance, Control, and Dynamics, 2016, 39(8): 1885-1890.
[5] Cho D, Kim H J, Tahk M J. Nonsingular Sliding Mode Guidance for Impact Time Control[J]. Journal of Guidance, Control, and Dynamics, 2016, 39(1): 61-68.
[6] Kumar S R, Ghose D. Impact Time Guidance for Large Heading Errors Using Sliding Mode Control[J]. IEEE Transactions on Aerospace and Electronic Systems, 2015, 51(4): 3123-3138.
[7] Kim H G, Cho D, Kim H J. Sliding Mode Guidance Law for Impact Time Control without Explicit Time-to-Go Estimation[J]. IEEE Transactions on Aerospace and Electronic Systems, 2019, 55(1): 236-250.
[8] 郭正玉, 韩治国. 基于快速非奇异终端滑模的多弹协同制导律设计[J]. 航空兵器, 2020, 27(3): 62-66.
Guo Zhengyu, Han Zhiguo. Multi-Missile Cooperative Guidance Law Design Based on Fast Non-Singular Terminal Sliding Mode[J]. Aero Weaponry, 2020, 27(3): 62-66.(in Chinese)
[9] Saleem A, Ratnoo A. Lyapunov-Based Guidance Law for Impact Time Control and Simultaneous Arrival[J]. Journal of Guidance, Control, and Dynamics, 2016, 39(1): 164-173.
[10] Kim M, Jung B, Han B, et al. Lyapunov-Based Impact Time Control Guidance Laws against Stationary Targets[J]. IEEE Transactions on Aerospace and Electronic Systems, 2015, 51(2): 1111-1122.
[11] Jeon I S, Lee J I, Tahk M J. Homing Guidance Law for Cooperative Attack of Multiple Missiles[J]. Journal of Guidance, Control, and Dynamics, 2010, 33(1): 275-280.
[12] Zadka B, Tripathy T, Tsalik R, et al. Consensus-Based Cooperative Geometrical Rules for Simultaneous Target Interception[J]. Journal of Guidance, Control, and Dynamics, 2020, 43(12): 2425-2432.
[13] 张振林, 张科, 郭正玉, 等. 一种新型领从式多弹协同制导律设计[J]. 航空兵器, 2020, 27(5): 33-38.
Zhang Zhenlin, Zhang Ke, Guo Zhengyu, et al. Design of a New Guidance Law for Guided Multiple Missiles[J]. Aero Weaponry, 2020, 27(5): 33-38.(in Chinese)
[14] Li K, Wang J N, Lee C H, et al. Distributed Cooperative Gui-dance for Multivehicle Simultaneous Arrival without Numerical Singularities[J]. Journal of Guidance, Control, and Dynamics, 2020, 43(7): 1365-1373.
[15] Kumar S R, Mukherjee D. Cooperative Salvo Guidance Using Finite-Time Consensus over Directed Cycles[J]. IEEE Transactions on Aerospace and Electronic Systems, 2020, 56(2): 1504-1514.
[16] Zhou J L, Yang J Y. Distributed Guidance Law Design for Coopera-tive Simultaneous Attacks with Multiple Missiles[J]. Journal of Guidance, Control, and Dynamics, 2016, 39(10): 2439-2447.
[17] 呂腾. 基于一致性的多巡航导弹协同末制导律设计[D]. 哈尔滨: 哈尔滨工业大学, 2019.
Lü Teng. Consensus Based Cooperative Terminal Guidance Law Design for Multiple Cruise Missiles[D]. Harbin: Harbin Institute of Technology, 2019. (in Chinese)
[18] Olfati-Saber R, Murray R M. Consensus Problems in Networks of Agents with Switching Topology and Time-Delays[J]. IEEE Transactions on Automatic Control, 2004, 49(9): 1520-1533.
[19] Wang L, Xiao F. Finite-Time Consensus Problems for Networks of Dynamic Agents[J]. IEEE Transactions on Automatic Control, 2010, 55(4): 950-955.
[20] Ming C, Wang X M, Sun R S. A Novel Non-Singular Terminal Sliding Mode Control-Based Integrated Missile Guidance and Control with Impact Angle Constraint[J]. Aerospace Science and Technology, 2019, 94: 105368.
[21] 宋申民. 运动稳定性与航天控制[M]. 北京: 科学出版社, 2014.
Song Shenmin. Motion Stability and Aerospace Control [M]. Beijing: Science Press, 2014.(in Chinese)
Nonsingular Distributed Guidance Method for Time-Coordinated
Attack with Multiple Missiles
Yang Xiaoyan1,Zhang Jinpeng2,Ma Huimin2,Song Shenmin1*
(1. School of Aeronautics, Harbin Institute of Technology,Harbin 150001,China;
2. Aviation Key Laboratary of Science and Technology on Airborne Guided Weapons,Luoyang 471009,China)
Abstract: A nonsingular distributed cooperative terminal guidance law is proposed for the problem of multiple missiles attacking ground stationary target simultaneously. By selecting the estimated attack time as consistency variable, the consistency algorithm is combined with nonsingular guidance law, and the limitation caused by the assumption of small angle and specified attack time can be avoided. The closed-loop stabilities of the consensus error and the lead angle are proved based on Lyapunov stability theory, which can verify the effectiveness of the proposed distributed cooperative guidance law. Numerical contrast simulations further verify that the miss distance of the designed guidance law under large initial lead angle is one order of magnitude smaller than that of the compared distributed guidance law, demonstrating the effectiveness and superiority of the proposed guidance law.
Key words: distributed;cooperative guidance;nonsingular;without small angle assumption;consistency algorithm;finite time; missile
收稿日期:2021-04-01
基金項目:航空科学基金项目(20170112012;20180112003)
作者简介:杨小艳(1995-),女,安徽阜阳人,博士研究生。
通讯作者:宋申民(1968-),男,山东滕州人,博士生导师。

