基于阶跃射流的撞击流反应器流场动态特性分析

张建伟，安丰元，董鑫，冯颖

（沈阳化工大学机械与动力工程学院，辽宁 沈阳 110142）

引 言

在化学生产以及多种过程工业中，撞击流是一种能显著提高传热传质性能的技术[1]，对微观混合效果有明显的促进作用[2]。与传统方法相比，撞击流反应器混合效率更高[3-8]。因此探究撞击流反应器内复杂流场特性对其应用至关重要。

关于撞击流反应器流场特性的研究主要集中在探究不同入口条件和几何结构下的撞击流反应器流场特性[9-13]。杜敏等[14]利用高速数码摄像系统对撞击流液滴碰撞后续行为进行研究，结果表明改变撞击流反应器的入口条件，会对撞击流反应器内流场以及流体液滴后续发展产生重要影响，液滴粒径与进口速度增大，液滴更容易破碎。屠功毅等[15]通过数值模拟对不同雷诺数及喷嘴间距下平面撞击流进行研究，研究表明流体速度和喷嘴间距主要决定平面撞击流偏斜振荡周期。Zhang 等[16]利用粒子图像测速技术（PIV）研究了不同入口条件下三重射流撞击流反应器内的湍流特性，研究发现，减小射流间距会导致反应器内流体出现强烈湍流，同时改变入口雷诺数也会对流场湍流效果以及混合效率产生影响。Tsaoulidis 等[17]利用高速成像技术对反应器内的液-液分散进行研究，研究发现入口条件的改变对撞击流液滴的尺寸以及界面面积会产生重要影响，减小喷嘴直径会使液滴尺寸更小，增大入口速度会使流场内液滴更加分散。张建伟等[18]利用平面激光诱导荧光技术（PLIF）对撞击流反应器内液体混合时浓度场变化进行研究，结果表明改变喷嘴间距会对完全混合时间产生影响，最佳喷嘴间距为L=3D。Zhang 等[19]通过平面激光诱导荧光技术（PLIF）并运用POD 方法对不同条件下撞击流反应器浓度场进行研究，发现非对称流场的能量始终高于对称流场。

动态撞击流反应器是在其他条件相同的情况下，将喷嘴入口的稳态输入变为动态输入，使喷嘴入口速度实现有规律的变化，从而达到对撞击流反应器中的流场进行动态调节的目的[20]。近年来部分学者对动态入口条件反应器进行研究。Liu 等[21]采用粒子图像测速技术（PIV）对动态入口条件反应器流场特性进行研究，得出动态入口速度条件对增加流场湍动效果起着重要作用。通过合理设计入口速度条件，可以使流场内流体湍动更剧烈并改善混合效果[22]。研究动态撞击流反应器流动特性的意义在于可以优化传统稳态入口条件对称撞击流反应器[23]。

动态入口条件会对撞击流反应器的流场特性产生很大影响，因此可以通过设计不同形式入口射流对流场进行激励与强化。刘娇[24]通过数值模拟与可视化实验对动态混合器的混合性能进行研究，结果表明动态射流相比于传统的稳态射流，可以使流场扰动增加，更利于混合。稳态对称撞击流反应器虽然在撞击区流体活跃程度很高，但在撞击流反应器内仍然存在一些“死区”[25-26]，不利于物料的充分混合，而动态调节可以增强整个流场的扰动，加强流场内流体的湍动。因此，关于动态撞击流反应器的流场特性方面还需要深入研究，相关研究对优化流场速度分布和设计较强湍流特性的撞击流反应器有一定的参考价值。

本文针对不同阶跃型入口条件下撞击流反应器，采用实验与数值模拟方法对水平同轴动态撞击流反应器的流场特性进行分析。通过分析反应器内湍流强度、湍动能、螺旋度等参数，来探究动态入口条件对反应器流动特征的影响，并对比动态撞击流反应器与稳态撞击流反应器的流动特征、湍流特性与能量水平。

1 动态撞击流反应器流场数值模拟

1.1 流体运动方程

本文采用Realizablek-ε模型进行数值模拟。Realizablek-ε模型增加了旋转和曲率等相关内容，对流体的正应力进行某种数学约束，适用于管道内流动、射流以及带有分离的流动等[22]。因此本研究所使用的物理模型适合运用Realizablek-ε模型进行求解计算，湍流动能(k)和湍流耗散率(ε)输运方程如下：

1.2 物理模型

1.2.1 模型与边界条件 反应器的几何模型由一个直径130 mm、高500 mm 的圆柱筒体及两个喷嘴构成。喷嘴位于反应器Y方向正中，出口位于反应器上部，如图1所示。

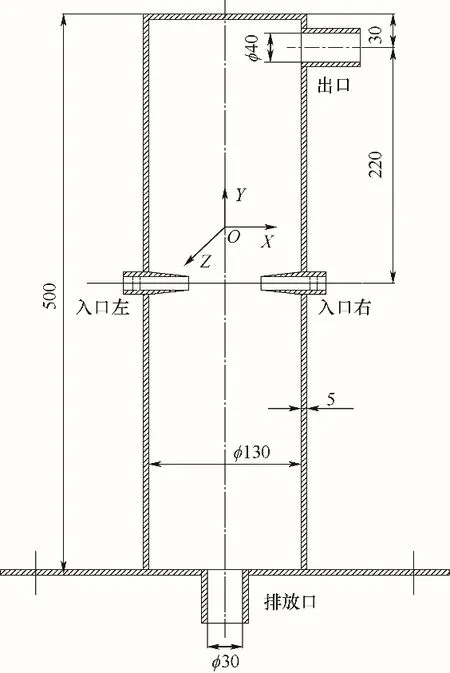
图1 撞击流反应器示意图Fig.1 Schematic diagram of the impinging stream mixer

在笔者前期的研究中，确定了水平对置撞击流反应器混合的最优工况：喷嘴间距L=3D[27]，喷嘴直径D为10 mm[28]，本文在此基础上进行数值模拟研究。喷嘴入口设置为速度入口（velocity-inlet）边界条件，出口设置为外流（outflow）边界条件，其余设置为固壁无滑移光滑的壁面（wall）边界条件。采用SIMPLEC 算法求解流体压力与速度耦合。压力方程采用二阶格式，动量方程采用有界中心差分格式，能量方程采用二阶迎风格式。采用瞬态计算，瞬态公式采用有界二阶隐式。时间步长为0.01 s。

1.2.2 网格划分 为了探究网格数量对数值计算的影响，利用ICEM 模块构建330591，396521，559074，608371，788332，931245，1217361，1323737八组数量的非结构化网格模型。保持其他条件相同的情况下，探究不同数量网格对撞击驻点的速度的影响，如图2所示。

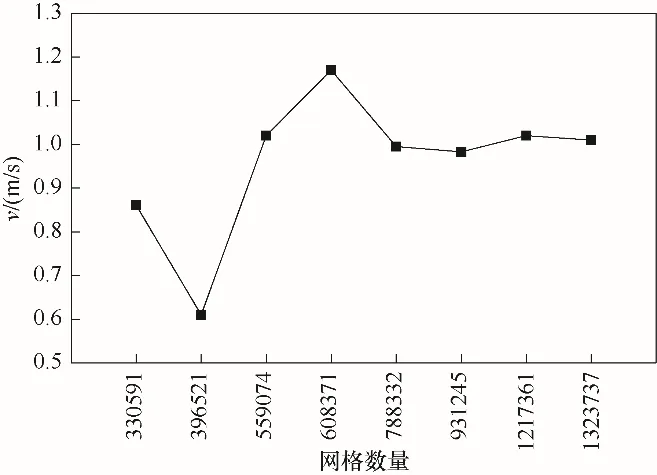
图2 不同网格数量下撞击驻点速度Fig.2 The stagnation point speed under different number of grids

从图2 可以看出，当网格数量较少时（30 万～60万），对计算结果的影响比较大。当网格数量达到788332 后，计算数据趋于平稳，数据前后差异小于3%，可以初步认为对于本模型网格数量达到80 万以后，网格数量对计算精度影响不大。为了进一步验证，取数量分别为788332，931245，1217361，1323737 的四种网格，得到不同网格数量对应的撞击轴线上各点速度分布，如图3所示。

图3 表明，撞击轴线处流体的速度分布最大差异小于3%，因此对于本模型，可认为当网格数量达到80万个以后，网格数量对计算精度影响不大。因此为了减少模拟计算时间和保证计算精度，本文采用931245数量网格进行数值模拟计算。

图3 不同网格数量下撞击轴线速度分布Fig.3 The distribution of velocity of impact axis under different grid numbers

1.2.3 数值模拟工况条件 本文采用阶跃型（step）入口速度条件对撞击流反应器进行调节，对于阶跃型速度入口条件，需要通过用户自定义函数（user defined function，UDF）来进行设置与编译，然后导入仿真软件进行解释和运算。为了方便探究与讨论，利用ω代表动态调节的周期进程，ω=1为一个周期。动态入口条件两侧入口速度不相等，并且速度大小在不停变化中，但在不同周期内，左右两侧入口平均速率是相等的；与动态入口条件相对应的稳态入口条件速度值保持为平均速率（vaver）。本文设置四种不同入口平均速率以及三种不同入口速率差下的动态入口条件，入口工况条件如表1所示，入口流型如图4所示。

图4 入口速度绝对值Fig.4 The absolute value of inlet velocity

表1 入口工况条件Table 1 Inlet condition

1.3 实验验证与分析

本实验采用二维高速粒子图像测速（TR-PIV）技术系统进行测量，示踪剂选用空心玻璃球（密度为1.05～1.15 g/cm3，粒径为10～15 µm）。采用CCD摄像机进行拍摄（图像采集窗口大小为1440×1920）,采集频率为15 Hz。采用两个变频器分别对两个水泵进行调节，从而使撞击流反应器的入口速度呈现阶跃变化，实验系统如图5所示。

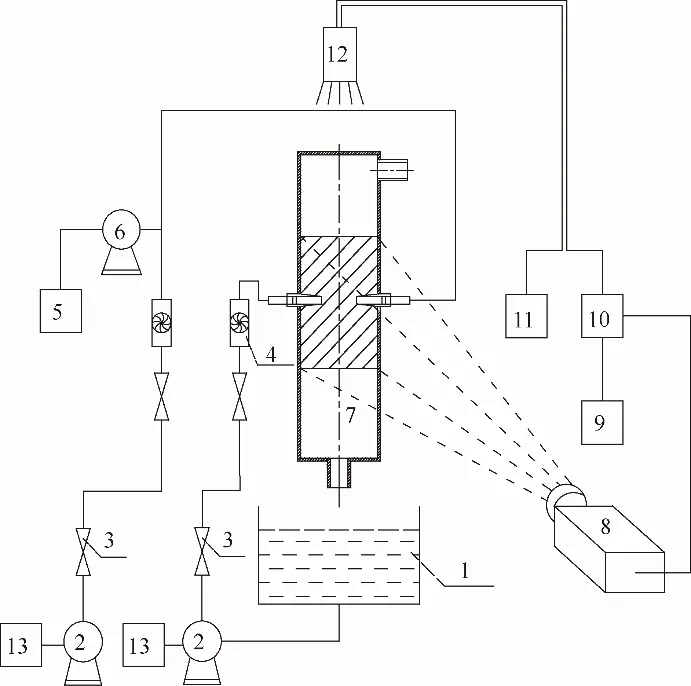
图5 实验系统示意图Fig.5 The schematic diagram of experimental system

图6为不同时刻动态撞击流反应器内XOY平面流体运动图像，可以看出在加入动态调节后，入口速度不断变化，撞击面不再稳定于两喷嘴中心处，而是在两喷嘴之间移动。由于撞击面的不断移动，撞击面上下两侧流体向入口速度小的方向偏移。高流速、高剪切的流体会从撞击面延伸至喷嘴上下两侧近壁面处，可以有效增加低流速区的扰动。

图6 不同时刻下流场内撞击面移动情况Fig.6 The movement of impact surface in flow field at different time

对实验得到的数据进行分解，将流体速度分解为水平方向分速度U，竖直方向分速度V。对ω=0.4时撞击轴线U方向分速度进行测量和计算。如图7所示，速度最低值位于撞击中心，由于两侧入口动量的不平衡，驻点向速度小的一侧偏移，平均误差12.4%，CFD模拟结果与PIV实验数据基本吻合。

图7 ω=0.4时撞击轴线U方向分速度绝对值的PIV和CFD结果Fig.7 The PIV and CFD results in the component of absolute velocity in U direction of impact axis at ω=0.4

为了研究撞击轴线上流体旋转情况与流动状态，计算ω=0.4 时撞击轴线的涡度绝对值，如图8 所示。涡度绝对值沿着撞击中心向两侧扩展而逐渐减小，驻点处涡度达到最大值，说明流体受到较大剪切作用。由于反应器内两侧入口速度不同，峰值向速度小的一侧偏移，平均误差12.9%，CFD 模拟结果与PIV实验数据基本吻合。

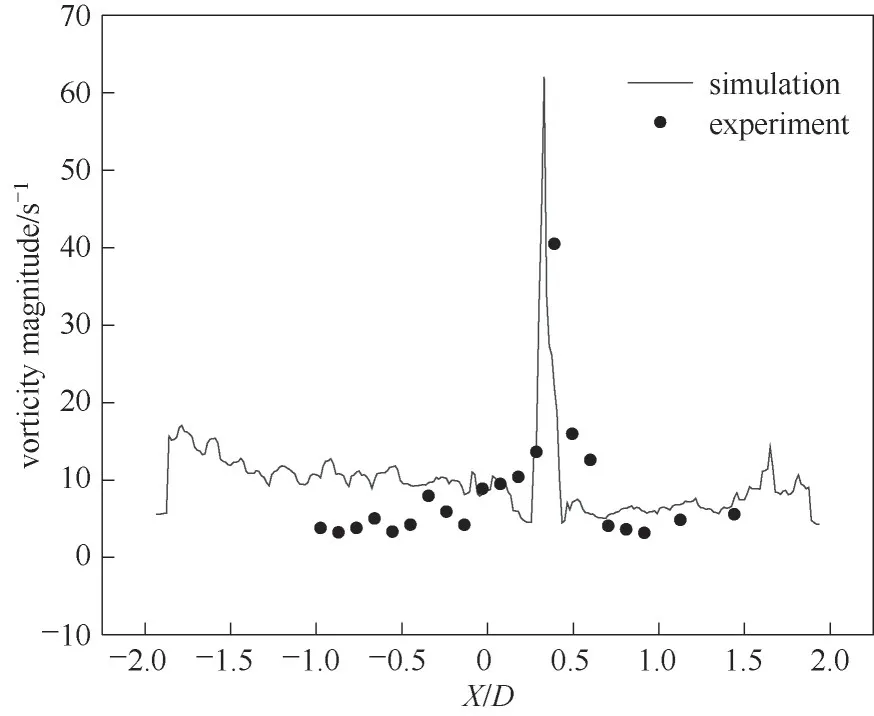
图8 ω=0.4时撞击轴线涡度绝对值PIV和CFD结果Fig.8 The PIV and CFD results of vorticity absolute value on impact axis at ω=0.4

2 结果讨论与分析

2.1 动态与稳态撞击流反应器流场特性对比

2.1.1 反应器内流动特征对比 为了探究动态入口条件对流场的影响，得到动态条件与稳态条件下撞击轴线的速度分布，如图9 所示。动态与稳态条件下撞击轴线上流体最低速度存在于撞击中心，且流体速度都随着撞击中心的轴向延伸而逐渐增大。动态条件下撞击驻点偏移到入口速度较低的一侧，且撞击驻点的速度低于稳态条件下的撞击驻点速度约15%。原因是动态条件下两侧入口存在速度差，导致驻点两侧流体流动状态不平衡，驻点处流体碰撞更加强烈。

图9 稳态与动态条件撞击轴线速度绝对值Fig.9 The absolute velocity of impact axial under steady and dynamic conditions

相较于稳态条件，动态入口条件可以加强反应器内流场扰动，探究动态入口条件与稳态入口条件下流体的运动，得到动态与稳态条件下XOY平面的流体轨迹图，如图10所示。在稳态对称撞击流反应器中，撞击区流动状态是关于撞击面对称的，且传质主要发生在撞击区，这就导致在整个撞击流反应器两侧存在流体流速较小、流动状态不佳的区域。稳态条件下反应器中撞击面上下两侧会出现成对存在的旋涡，旋涡在反应器XOY平面几何中心径向分布，如图10（a）所示。而当入口条件为动态的情况下，两流体依然相向运动形成撞击区，但是流场的流动状态不再关于撞击面对称，成对存在的旋涡向流体速度小的一侧偏移并延伸至壁面，流场内也出现更多旋涡，如图10（b）所示。原因是动态条件下撞击面随着入口条件的不均衡而在两喷嘴之间周期性移动。两侧入口输入动量不平衡，流场内流体更加紊乱与无序，流体的卷吸会延伸至壁面，旋涡形成与破碎使能量的集聚与耗散的频率更高，更加利于混合与相间传递。

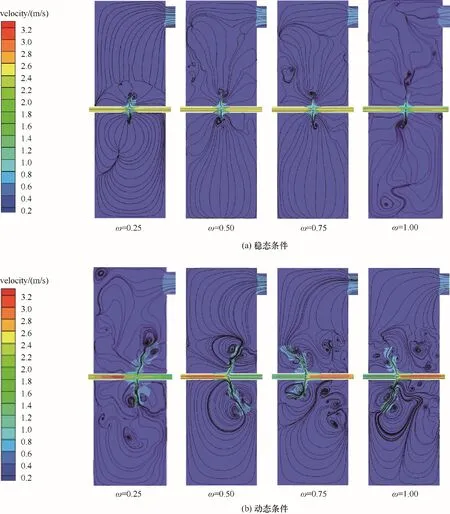
图10 稳态与动态条件下反应器内流体轨迹Fig.10 The flow trajectory in reactor under steady and dynamic conditions

为了研究撞击轴线上流体旋转程度，对比分析动态与稳态条件下撞击轴线上流体螺旋度[29]，计算公式为：

如图11所示，可以看出稳态撞击流反应器撞击轴线上的螺旋度值较小，只在撞击面附近有小幅波动，动态条件下撞击面处的流体螺旋度出现较大峰值，说明撞击轴线上流体受到较大剪切作用力。图12 所示为动态与稳态条件下不同时刻撞击轴线上螺旋度绝对值，可以看出，随着周期变化动态条件下撞击轴线上螺旋度平均值均大于稳态条件。原因是动态撞击流反应器内两侧流体始终处于动量不平衡的状态，流体受到强烈挤压并在受到较大剪切作用后产生剧烈扰动，流体微团发生破碎。

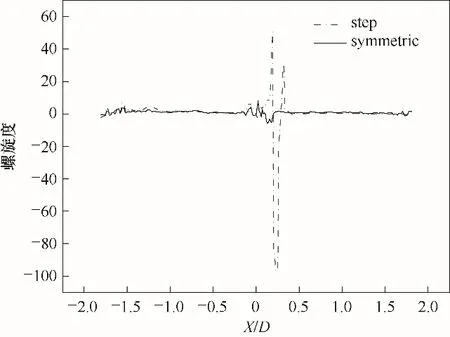
图11 稳态与动态条件下撞击轴线螺旋度分布Fig.11 The distribution of helicity on impact axis under steady and dynamic conditions

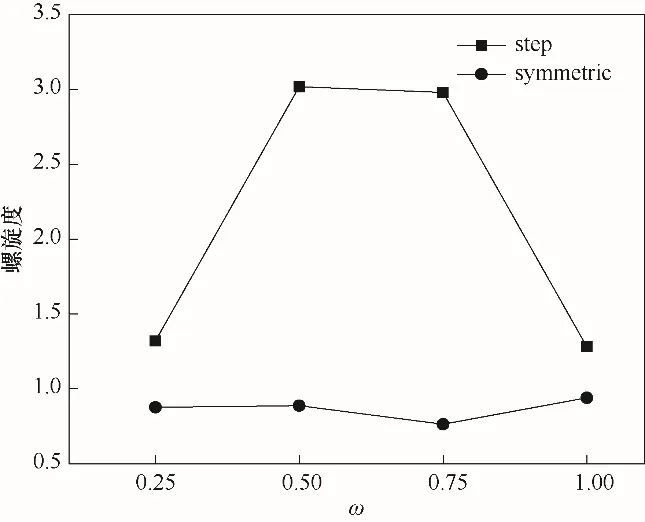
图12 稳态与动态条件下不同时刻撞击轴线平均螺旋度绝对值Fig.12 The absolute value of average helicity of impact axis at different times under steady and dynamic conditions

2.1.2 反应器内湍流特性对比 湍动能的大小与分布很好地反映了流场的湍动程度与混合效果。反应器中不同的操作条件以及不同的流动状态会对流场中的湍动能产生很大的影响[30]。为了对比动态撞击流反应器与稳态撞击流反应器的湍流特性，获得动态与稳态条件下XOZ平面湍动能分布，如图13 所示。可以看出稳态条件与动态条件下撞击区存在较大湍动能梯度。但动态条件下撞击区的湍动能梯度分布更广，湍动能数值也要大于稳态撞击流反应器。这是因为动态条件下反应器左右入口速度在不断变化，撞击区的能量分布更广，流体产生更强烈的脉动与能量传递。

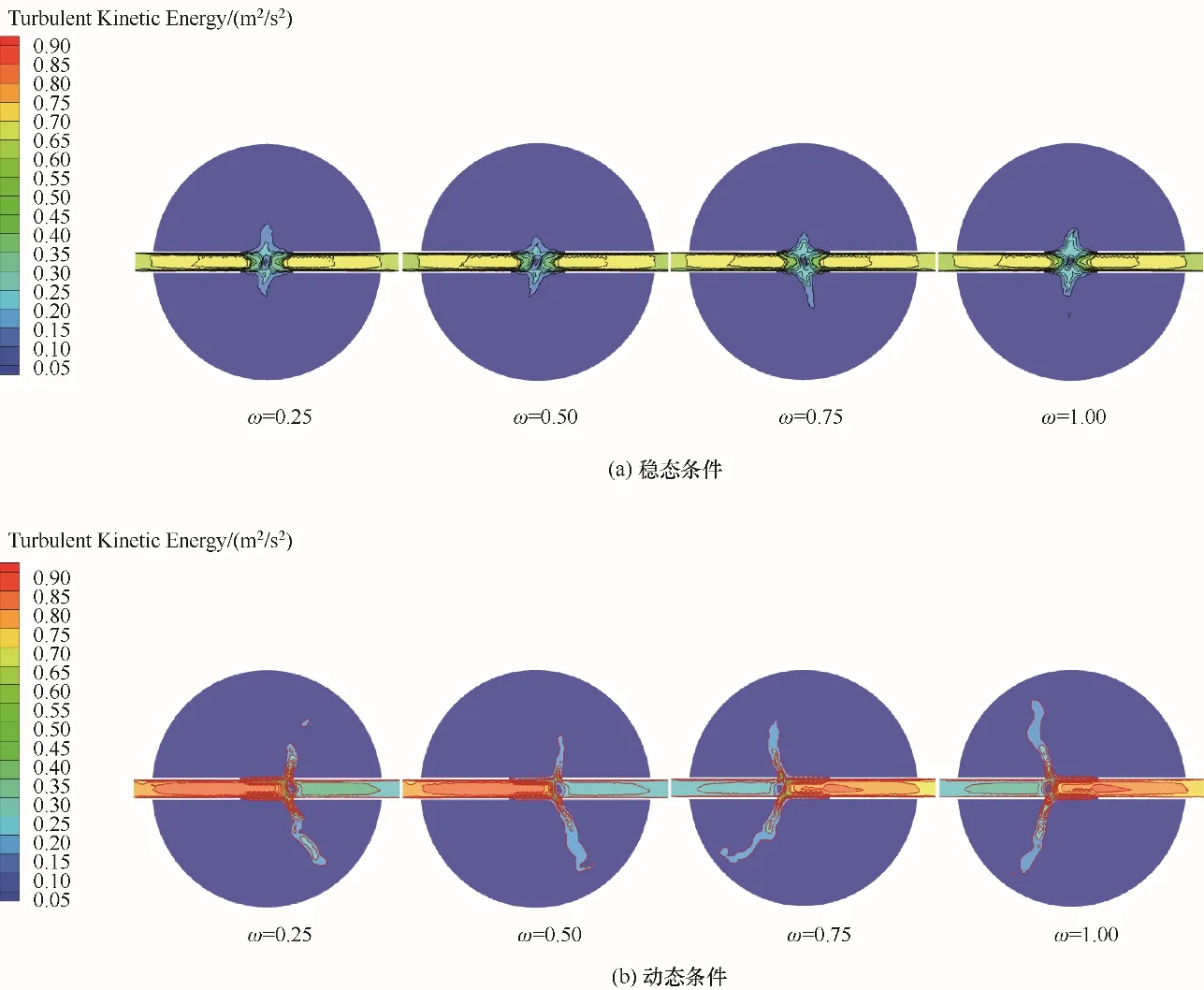
图13 稳态与动态条件下XOZ平面湍动能等值线图Fig.13 The isogram of turbulent kinetic energy at XOZ plane under steady and dynamic conditions

湍流黏度是湍流中由于速度脉动产生的运动阻力，本质是涡扩散，其反映的是流体的流动状态。流体处于湍流状态时，由于随机脉动造成强烈涡团扩散，旋涡带动流体质点随机运动导致强烈的动量传递。图14 所示为稳态与动态条件下撞击轴线湍流黏度随周期变化。可以看出随着周期变化，稳态条件下撞击轴线湍流黏度变化幅度很小，动态条件下撞击轴线湍流黏度平均大于稳态条件下52.6%，并且具有周期性。原因为动态条件下撞击轴线上产生了强烈的速度脉动，当动态调节周期发生变化时，流场内流体流动会受到更大的阻力，撞击区会出现更强烈的涡团扩散与动量传递。

图14 稳态与动态条件下撞击轴线平均湍流黏度Fig.14 The mean turbulent viscosity of impact axis under steady and dynamic conditions

2.1.3 反应器内能量水平对比 相比于稳态入口条件，动态入口条件能够强化能量传递，为了进一步分析动态入口条件对流场的影响，得到稳态与动态条件下2.5 周期内撞击轴线上的平均压力，如图15 所示。随着周期变化，稳态条件下撞击轴线上平均压力较小，动态条件下撞击轴线上的平均压力较大并呈现周期性；在周期变化的瞬间，撞击轴线会出现一瞬间负压。原因是入口条件的周期性变化会给流场带来巨大动量，撞击轴线上的流体在不断变化的冲击下产生高水平的压力，而高水平的压力会促进流体的剪切与微团的破碎，促进流体的混合与动量的交换。

图15 稳态与动态条件下撞击轴线平均压力变化Fig.15 The variation of mean pressure on impact axis under steady and dynamic conditions

进一步分析动态撞击流反应器能量变化情况，测量驻点速度在2.5 周期内的变化并对其进行频谱分析。如图16所示，稳态条件下只在低频区有小幅波动，动态条件下在低频区有较大波动并出现一个较明显的峰值。说明动态条件下流场中会产生更加集中的能量，低频区主要产生大涡[31]，因此动态条件下流场产生的大涡强度更大。进而说明大涡经过破碎分解，向径向输送更多小涡，流场能量释放得更完全。

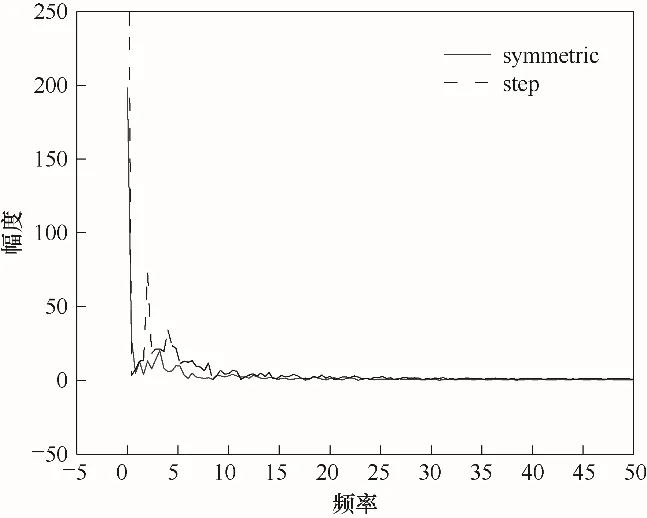
图16 稳态与动态条件下驻点速度变化频谱图Fig.16 The spectrum diagram of the stagnation point velocity under steady and dynamic conditions

为了进一步研究反应器内的流场能量水平，计算2.5周期内撞击驻点速度的功率谱，如图17所示。从功率谱图中可以看出，随着频率的增加，稳态条件和动态条件下的驻点速度功率都逐渐降低，不同频率下，动态条件下的流场功率都大于稳态条件。说明加入动态调节后，整个流场的能量水平提高，能量密度更加集中，高能量水平会促进流场内的微团破碎与混合。

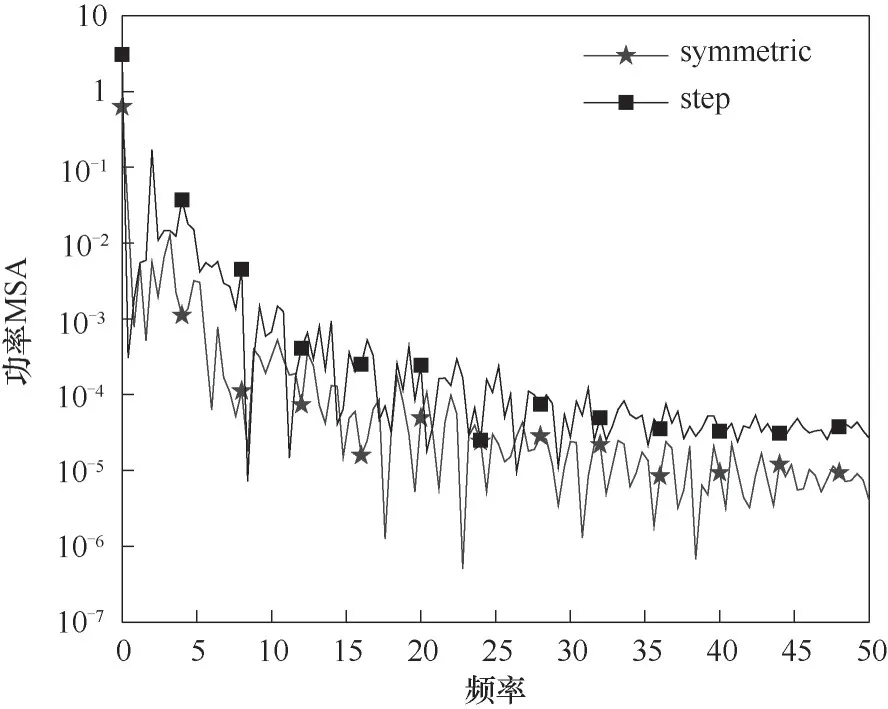
图17 稳态与动态条件下驻点速度功率谱图Fig.17 The power spectrum of stagnation point velocity under steady and dynamic conditions

2.2 不同阶跃射流下撞击流反应器流场特性

2.2.1 反应器内流动特征 撞击流反应器内两股流体同轴相向流动，在撞击面处撞击并转为径向运动，因此撞击驻点处存在巨大动量转换与能量交换。分析不同工况下驻点平均速度，如图18 所示。相同入口速率差下，随着入口平均速率的增大，驻点速度逐渐增大。在入口平均速率为1.5 与1.75 m/s 时，随着入口速率差的增大，驻点速度逐渐减小。原因是入口速率差越大，撞击面处的流体受到的动量不平衡越强烈。在入口平均速率为2 和2.25 m/s时，入口速率差为0.75 m/s 时驻点速度最低，说明在此工况条件下，流体撞击后动量转换更剧烈，能量释放更完全。

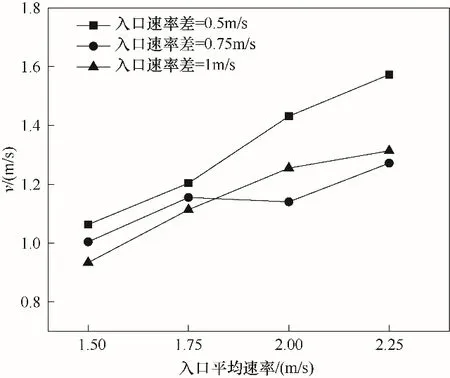
图18 不同工况下驻点平均速度Fig.18 The average velocity of stagnation point under different conditions

为了探究流场内流体流动情况，分析不同工况下撞击面的移动速度，如图19所示。相同入口平均速率下，随着入口速率差的增大，撞击面移动速度变快。速率差为1 m/s 时撞击面移动速度平均大于速率差为0.75 m/s 时撞击面移动速度约35%；大于速率差为0.5 m/s 时撞击面移动速度约260%。相同周期下，撞击面移动速度越快，撞击区在两侧的停留时间就越长，因此能有效解决两侧喷嘴上方流动状态缓滞的问题。

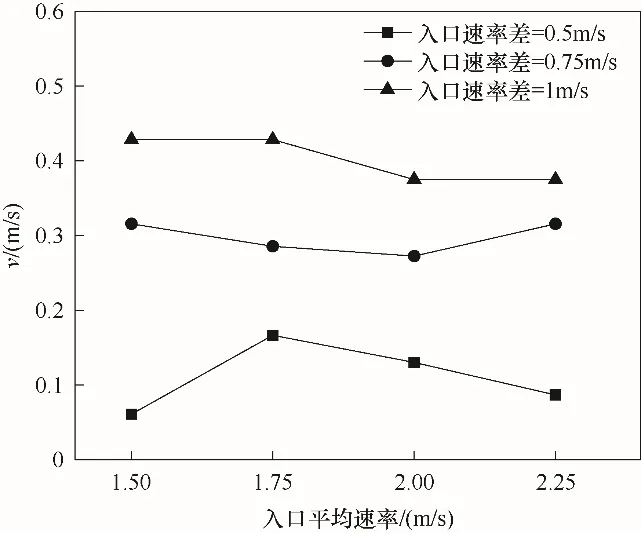
图19 不同工况下撞击面移动速度Fig.19 The movement speed of impact surface under different conditions

2.2.2 反应器内湍流特性 为了研究动态条件下流场的湍流特性，对不同阶跃工况下撞击轴线上的湍流强度进行分析，如图20所示。不同工况下撞击轴线上的湍流强度都呈现为单峰分布，撞击面上流体湍流强度达到最大值，由于存在入口速率差，湍流强度峰值偏向入口速度小的一侧。相同入口速率差下，随着入口平均速率的增大，湍流强度峰值逐渐增大。随着入口速率差的增大，撞击轴线上湍流强度峰值逐渐增大。说明增大入口速率差与入口平均速率能够增强撞击轴线上流体的湍动。

图20 不同工况下撞击轴线湍流强度Fig.20 The turbulence intensity of impact axis under different conditions

为了进一步探究动态条件下撞击流反应器内的湍流特性，分析一个周期内不同阶跃入口条件下XOZ平面的平均湍动能，如图21所示。可以看出相同入口速率差下，随着入口平均速率的增大，平均湍动能逐渐减小；相同入口平均速率下，随着入口速率差的增大，平均湍动能逐渐减小。

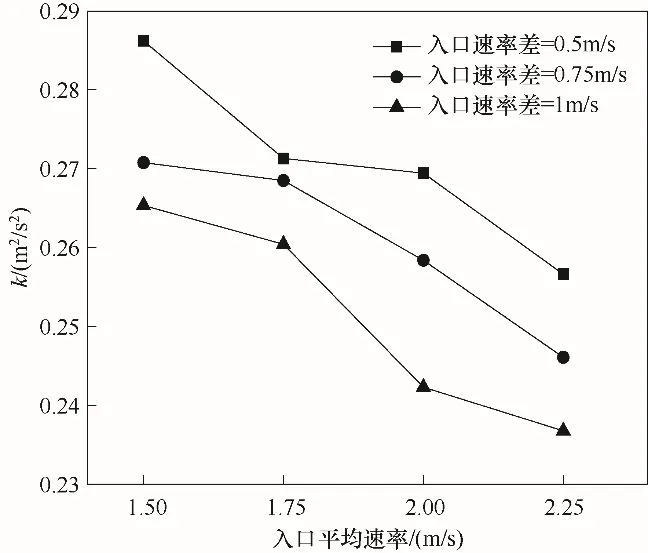
图21 一个周期内XOZ平面平均湍动能Fig.21 The mean turbulent kinetic energy on XOZ plane in one cycle

3 结 论

为了探究阶跃型入口速度对撞击流反应器流场特性的影响，本文运用实验与数值模拟方法对不同入口速度条件下动态撞击流反应器流场特征进行研究。通过分析流场的流动特征参数，并与稳态撞击流反应器的流场特性进行对比，得到以下结论：

（1）动态撞击流反应器内撞击面随着入口速度周期变化在左右两喷嘴之间不断移动，撞击区能够延伸至喷嘴上下壁面处。相同周期下，撞击面移动速度越快，撞击区在两侧停留时间就越长，因此能有效增加反应器内部分流动状态不佳区域的扰动，有利于混合。

（2）动态撞击流反应器内，增大入口速率差以及入口平均速率，能够显著加强反应器内轴向流体的湍动，并使径向上流体剧烈扰动。与稳态条件相比，动态入口条件下的流场湍动能以及速度脉动均高于稳态入口条件，流场更为“活跃”。

（3）在保持入口平均速率相同的情况下，相比于稳态，动态撞击流反应器内流场产生更大的能量，反应器内轴向能够产生强度更大的大涡，轴向的大涡为径向输送更多的小涡，在涡的形成与破碎的过程中，加剧了流场的扰动，为周围的流体释放了更多的能量，有利于混合以及传热传质。

符 号 说 明

I——湍流强度

k——湍动能，m2/s2

S——流体连续性方程源项

t——时间，s

u——流体矢量速度，m/s

v——入口速度，m/s

x,y——坐标变量

ε——湍流耗散率，m2/s3

μ——动力黏度，Pa·s

ρ——密度，kg/m3