腕臂应力分布与接触悬挂模态特性研究

马启明，吴积钦，谢东旭

0 引言

接触网是经由集电器向电力牵引单元提供电能的导体系统，由接触悬挂、支持装置、定位装置、支柱与基础等组成[1]。接触悬挂由接触线、承力索、吊弦等零部件构成，直接参与弓网受流，弓网间的动态性能直接影响列车的取流质量[2]。腕臂系统是接触悬挂的承载者，腕臂定位系统是弓网系统的关键结构，其可靠性影响列车的安全稳定运行[3]。研究腕臂系统的应力情况及接触悬挂的模态特性至关重要。

文献[4]对恶劣作业环境下接触网腕臂与绝缘 子之间受力情况进行了分析，但未对应力情况进行分析。文献[5]对接触网腕臂结构系统进行了系统的静力学、动力学仿真，但也未对腕臂系统的应力情况进行说明。文献[6]对13种具有代表性的腕臂结构有限元模型进行了静力分析、模态分析、谐响应分析和瞬态动力学分析，但均将腕臂系统与接触网进行分离，未进行系统考虑。文献[7]将受电弓采用三维柔性体模型等效，将吊弦视为仅承受拉力的非线性弹簧，接触网采用三维实体单元离散，通过弓网之间的接触实现弓网系统的耦合，但未搭建腕臂系统模型且未对接触网模态特性进行进一步研究。本文采用文献[8]中的建模方法，按照某既有线路参数建立腕臂系统-接触悬挂模型，对静力作用下腕臂系统的应力分布情况及接触悬挂模态特性进行详细分析。

1 腕臂系统-接触悬挂模型建立

某既有线路接触悬挂参数与腕臂系统参数如表1、表2所示，线路实际布置情况如图1所示。

表1 接触悬挂参数

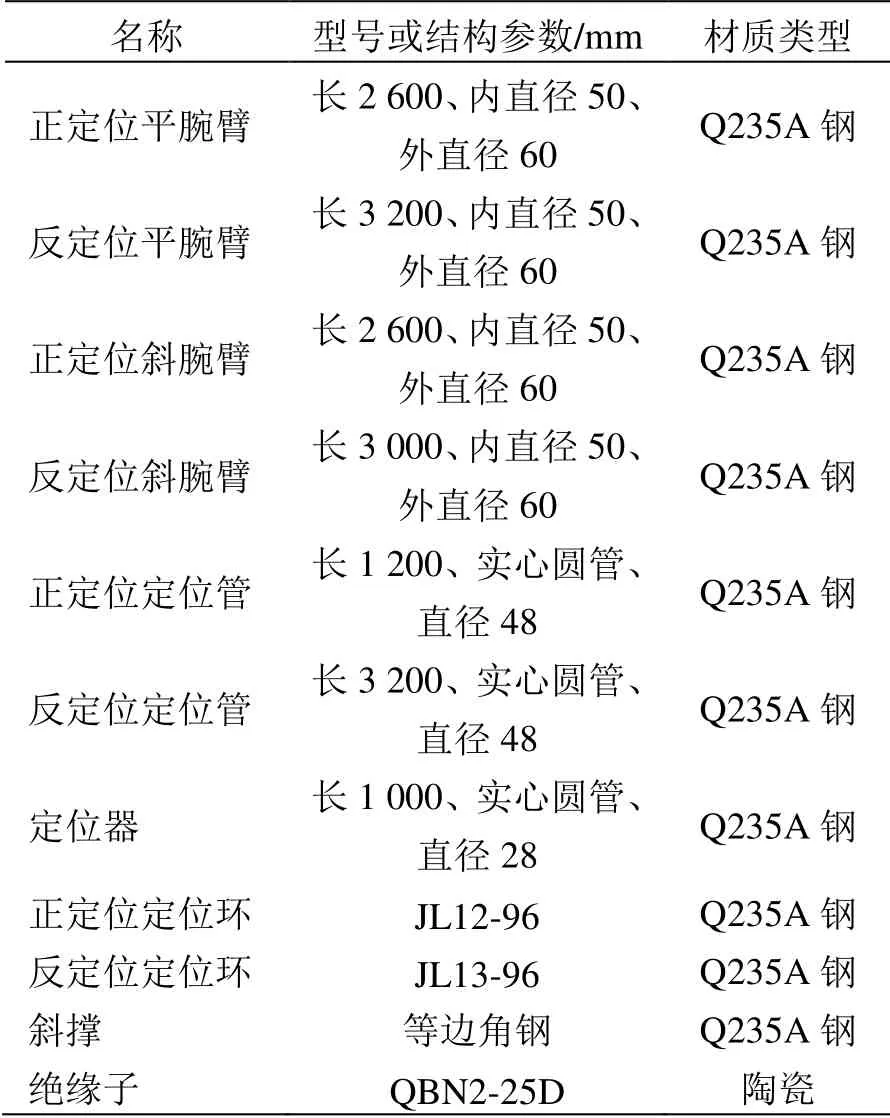
表2 腕臂系统参数

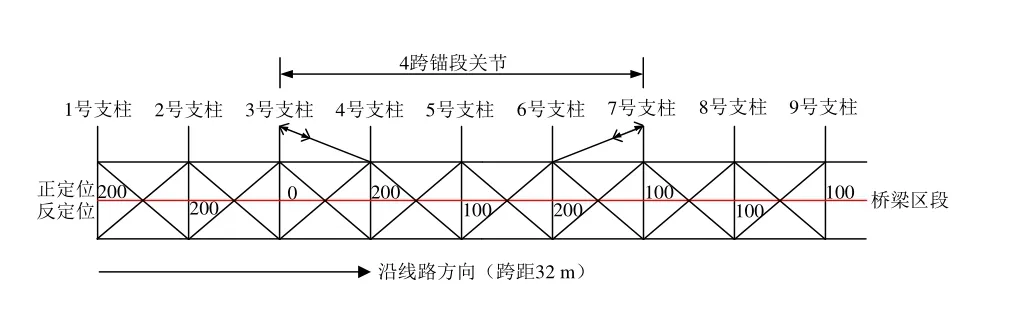
图1 既有线路现场情况

根据上述参数在ANSYS中建立包含4跨锚段关节在内的共8跨256 m的腕臂系统-接触悬挂仿真模型，如图2所示。

图2 腕臂系统-接触悬挂仿真模型

对图2所示腕臂系统安装位置设定全约束，将定位环与定位钩结合位置释放刚体连接，设置为球铰并将拉出值所在方向的旋转进行约束。关于接触网模型使用的仿真单元，参照文献[7]中的相关内容进行设定，本文不再赘述。腕臂系统需要考虑其外形对结构性能的影响，本文采用beam188三维空间梁单元进行模拟，beam188单元符合Timoshenko梁[9，10]理论，其动力学方程为

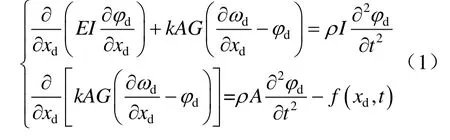
式中：ρ为beam188单元质量密度；I为beam188单元轴向惯性矩；G为beam188单元剪切模量；E为beam188单元弹性模量；A为截面积；φd为beam188单元转角位移；ωd为beam188单元平动位移；xd为beam188单元轴向位移；f(xd,t)为beam188单元载荷分布；k为Timoshenko剪切系数。

文中所提到的静力包括接触线张力、承力索张力及系统所受到的重力，下文将对静力作用下腕臂系统应力进行详细分析。

2 静力作用下腕臂系统的应力情况

提取静力作用下1～9号腕臂系统的应力情况如图3所示。 由图3可知：1号格构钢支柱承载的腕臂系统最大应力为8.58 MPa，位于平腕臂绝缘子安装末端；2号格构钢支柱承载的腕臂系统最大应力为13.8 MPa，位于斜腕臂绝缘子安装末端；3号格构钢支柱承载的腕臂系统最大应力为18.3 MPa，位于斜腕臂与平腕臂交叉安装点处；4号格构钢支柱承载的腕臂系统最大应力为29.8 MPa，位于非工作支斜腕臂绝缘子安装末端；5号格构钢支柱承载的腕臂系统最大应力为10.5 MPa，位于非工作支斜腕臂与平腕臂交叉安装点处；6号格构钢支柱承载的腕臂系统最大应力为43 MPa，位于非工作支斜腕臂绝缘子安装末端；7号格构钢支柱承载的腕臂系统最大应力为13.8 MPa，位于斜腕臂与平腕臂交叉安装点处；8号格构钢支柱承载的腕臂系统最大应力为11.1 MPa，位于斜腕臂绝缘子安装末端；9号格构钢支柱承载的腕臂系统最大应力为7.01 MPa，位于平腕臂绝缘子安装末端。可以看出，腕臂系统的最大应力常位于斜腕臂、平腕臂绝缘子安装末端或斜腕臂与平腕臂交叉安装点处，最大应力为43 MPa，可见不同零件的连接位置可能会产生应力集中，若进行动态分析，需对上述位置的应力情况进行重点分析。

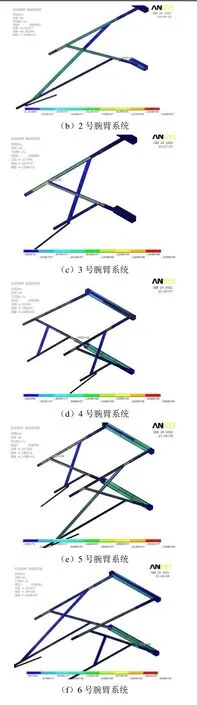
图3 静力作用下腕臂系统应力情况

综合1～9号腕臂系统的等效应力来看，整体处于低应力状态，均为弹性形变，未发生塑性形变。但绝缘子由陶瓷制成，属于脆性材料，且应力最大位置多出现于此，在长期运行过程中承受交变应力可能会引起疲劳。斜腕臂与平腕臂交叉安装点处的应力也相对突出，在安装时也需保证二者的紧固连接，降低施工误差。

3 接触悬挂模态分析

由文献[1]可知，接触网是一个具有多自由度的振动系统，该系统存在大量的固有振动频率。对于由相等跨距组成的链形悬挂，存在着对称和反对称两种振动方式。反对称振动方式下，基波波长等于跨距的2倍，如果将振动波理解为静止波，其固有频率为

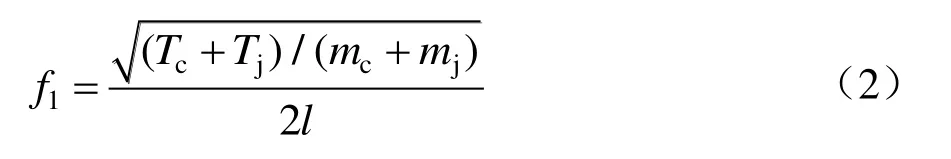
对称振动方式下，还应考虑第一吊弦所在段，其固有频率为

式中：Tc为承力索张力；Tj为接触线张力；mc为承力索质量密度；mj为接触线质量密度；l为跨距；l1为距定位点最近的两吊弦的间距。

根据上述计算式可得接触悬挂的固有频率：f1= 1.64 Hz、f2= 1.42 Hz。现提取静力下接触悬挂的10阶模态振型频率，如表3所示。

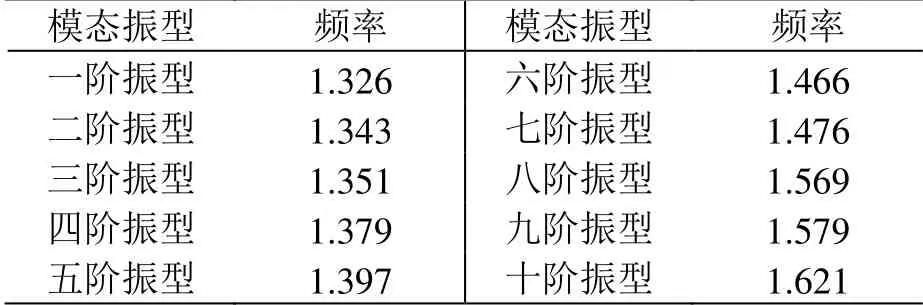
表3 接触悬挂10阶模态振型频率 Hz

将表3中的10阶模态振型频率对照f1、f2可知计算基本无误，绘制接触悬挂10阶模态振型如图4所示。

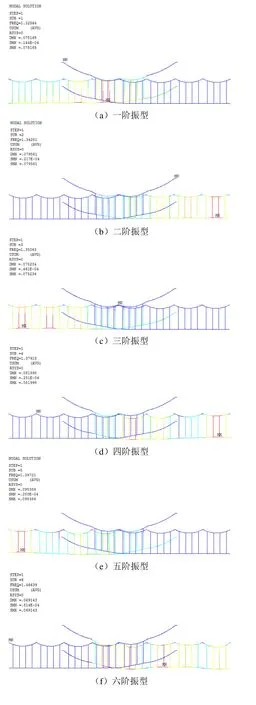
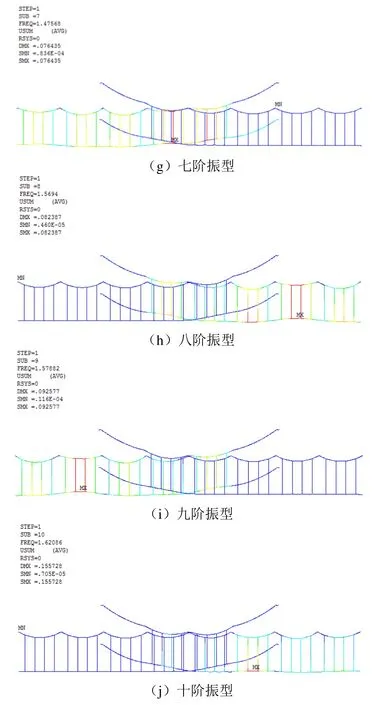
图4 接触悬挂10阶模态振型

由图4可知：一阶振型对应的频率为1.329 Hz，第一锚段接触线沿X正方向移动40.23 mm，且在Y正方向均有所抬升，抬升量最大值为64.03 mm，该位置位于锚段关节处；二阶振型对应的频率为1.343 Hz，第二锚段接触线在Y正方向均有所抬升，抬升量最大值为79.52 mm，位于第二锚段最后一跨接触线跨中位置；三阶振型对应的频率为1.351 Hz，第一锚段接触线在Y正方向均有所抬升，抬升量最大值为67.39 mm，位于第一锚段第一跨接触线跨中位置；四阶振型对应的频率为1.379 Hz，第二锚段接触线在Y正方向均有所抬升，较二阶振型相比抬升更加明显，最大值为81.35 mm，位于第二锚段最后一跨接触线跨中位置；五阶振型对应的频率为1.397 Hz，第一锚段接触线沿X正方向移动24.23 mm，且在Y正方向均有所抬升，抬升量最大值为91.98 mm，位于第一锚段第一跨接触线跨中位置；六阶振型对应的频率为1.466 Hz，第二锚段接触线在Y方向发生正弦式形变；七阶振型对应的频率为1.476 Hz，第一锚段接触线在Y方向发生正弦式形变，最大值为70.57 mm，位于锚段关节处；八阶振型对应的频率为1.569 Hz，第二锚段接触线在Y方向发生正弦式形变，且6号格构钢支柱与7号格构钢支柱间的接触线跨中位置沿Z正方向偏移56 mm；九阶振型对应的频率为1.579 Hz，第一锚段接触线在Y方向发生正弦式形变，最大值为70.57 mm，位于2号格构钢支柱与3号格构钢支柱间的接触线跨中位置；十阶振型对应的频率为1.621 Hz，6号格构钢支柱与7号格构钢支柱间的接触线跨中位置沿Z正方向偏移154.2 mm，严重影响拉出值的大小。

由以上分析可知，接触悬挂的固有频率主要集中在低频段内，当外部输入激励的频率与接触悬挂的固有频率接近时，接触悬挂振动程度增强，此时弓网系统动态作用稳定性会降低，易发生弓网接触力波动加剧，甚至出现弓网离线造成拉弧燃弧，影响接触网设备寿命。

4 结论

接触网的腕臂系统承载着接触悬挂与受电弓进行动态取流，腕臂系统的应力突出位置应引起关注，在日常运维中定期检查维护，一旦产生疲劳，易造成接触网坍塌引发重大事故；接触悬挂需要与受电弓直接作用，会导致两个相互独立的振动子系统间产生动态作用，若要避免接触悬挂共振，保持弓网动态运行的稳定性，必须对接触悬挂的模态特性进行分析。

本文结合某既有线路参数建立腕臂系统-接触悬挂模型，对腕臂系统静力作用下应力分布情况及接触悬挂模态特性进行了详细分析，得到以下结论：

（1）腕臂系统整体处于低应力状态，未发生塑性形变，应力最大位置多出现于绝缘子安装末端，长期的运行可能会引起疲劳。斜腕臂与平腕臂交叉安装点处的应力也相对突出，在安装时需保证平、斜腕臂的紧固连接，降低施工误差。

（2）接触悬挂的固有频率集中在低频段内，当外部输入激励的频率或弓网间作用频率与接触悬挂的固有频率接近时，接触网振动加剧，弓网系统动态作用稳定性降低，易使弓网接触力波动增强，甚至出现弓网离线，造成拉弧燃弧，影响接触网设备寿命。