水溶液中溶质的扩散同位素分馏研究

张霁云, 金 彪*, 张 干

水溶液中溶质的扩散同位素分馏研究

张霁云1, 2, 3, 金 彪1, 2, 3*, 张 干1, 2

(1. 中国科学院 广州地球化学研究所有机地球化学国家重点实验室, 广东 广州 510640; 2. 中国科学院深地科学卓越创新中心, 广东 广州 510640; 3. 中国科学院大学, 北京 100049)

稳定同位素分析是判定水溶液中溶质的组成、来源、迁移和转化过程与规律的重要工具, 在自由扩散等物理化学作用下, 对溶质的同位素分馏研究是稳定同位素技术应用的重要基础。本研究介绍了溶质的扩散过程与其同位素分馏效应之间的联系, 论述了研究溶质扩散过程中引入的稳定同位素分馏现象的意义, 描述了水溶液中溶质扩散的不同模拟实验方法及相关研究进展, 总结分析了包括扩散系数、质量相关性等因素的影响, 并介绍了基于水膜理论和分子动力学模型模拟阐释溶质扩散同位素分馏机理的相关研究成果, 对今后的研究趋势和主要任务进行了展望。

水溶液; 扩散; 同位素分馏

0 引 言

水相系统是最重要的环境地球化学系统之一。采用同位素分析方法, 研究溶质的稳定同位素分馏效应, 从而解释水溶液中物质的组成、来源、迁移和转化过程与规律, 已经成为目前环境地球化学研究的重要内容。

在水溶液中, 同位素分馏是物理、化学和生物等复杂过程共同作用的结果。目前普遍认为扩散、弥散和吸附等物理过程导致的同位素分馏效应远小于化学和生物过程(Hofstetter et al., 2008), 因此在大多数机制研究和应用实例中, 扩散过程引起的同位素分馏效应往往被忽略。然而对于地下水和沉积物孔隙水等迟缓水体而言, 由于水体流动和混合等水动力过程较弱, 扩散过程对溶质迁移及其相应的同位素分馏的影响将会明显增大, 此时如果忽略扩散过程导致的同位素分馏效应, 就有可能导致对溶质的来源组成、转化程度和途径产生误判。因此, 在环境地球化学系统的模型研究与实际应用中, 扩散同位素分馏的影响不容忽视。

目前, 通过单一过程制约的自由扩散模拟实验, 一系列重要组分或物质的扩散系数与扩散同位素分馏程度得以陆续确定, 包括主要离子(K+, Na+, Ca2+, Mg2+, Ba2+, Fe2+, Fe3+, Zn2+, Li+, Cl−和Br−) (Kunze and Fuoss, 1962; Pikal, 1972; Rodushkin et al., 2004; Richter et al., 2006; Eggenkamp and Coleman, 2009; Bourg et al., 2010; van Zuilen et al., 2016)和重要的稀有气体与温室气体(He, Ne, Ar, Kr, Xe, CO2, CH4和C2H6)(Oleary, 1984; Jähne et al., 1987; Zhang and Krooss, 2001; Schloemer and Krooss, 2004; Tempest and Emerson, 2013; Tyroller et al., 2014, 2018)。同时大量研究进行了模拟实验并定量分析了重要的地下水有机污染物(顺二氯乙烯、1,2-二氯乙烷和三氯乙烯)和代表性的有机物(氘代或非氘代异丙醇、叔丁醇、全氘代或非氘代的苯、甲苯和乙苯等)的C, H, O同位素分馏效应(LaBolle et al., 2008; Jin et al., 2014; Wanner and Hunkeler, 2015; Rolle and Jin, 2017)。在同位素分馏机制分析方面, 基于扩散模拟实验结果, 结合扩散系数的质量相关性, 以及水膜理论得以提出并用于解释不同组分扩散同位素分馏的差异(Richteret al., 2006)。同时分子动力学领域的Molecular dynamic (MD)计算模型被引入, 实现了在微观尺度模拟溶质扩散同位素分馏(Bourg and Sposito, 2007; Bourg et al., 2010)。

本研究旨在总结水相扩散实验及已获得的相关实验数据, 讨论不同目标溶质的扩散同位素分馏效应以及同位素体扩散系数的质量相关性, 并对扩散同位素分馏研究的未来发展方向进行展望。

1 扩散同位素分馏概述

在水溶液中, 溶质的迁移转化涉及一系列物理、化学和生物地球化学过程, 认识这些过程的同位素分馏效应, 有利于准确解析溶质的“同位素指纹”信息, 并通过同位素方法进行溶质源解析和化学过程分析。其中物理过程主要包括水流混合过程、扩散、弥散和吸附等。对于较强水动力条件下的水体(河流、湖海等), 由于流速快、混合作用强, 水体中物质分布较为均匀, 溶质受水体机械迁移影响比较显著, 扩散过程的影响通常可以忽略。然而在较弱水动力条件的迟缓水体中(地下水和沉积物孔隙水等), 扩散过程会对溶质的同位素示踪过程产生不可忽略的影响, 因此研究扩散同位素分馏及相应分馏机理对了解此类水体中溶质的迁移与转化具有重要意义。

自由扩散过程是指在特定介质中, 物质在浓度差的驱动下趋向于均匀分布的动力学过程。自由扩散过程受溶质类型、介质类型和环境温度等条件的影响, 其时空分布变化可以通过Fick’s扩散定律来表达(Fick, 1855):

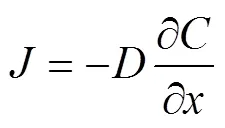
式中:表示位置的扩散通量, 通量大小与浓度梯度成正比;为扩散系数, 是与溶剂、溶质性质和环境动力学条件相关的综合参数, 其决定了特定条件下溶质的扩散能力。扩散方向与浓度递减的方向相同。在已知通量的基础上, 其浓度分布随时间的变化可以表示为:

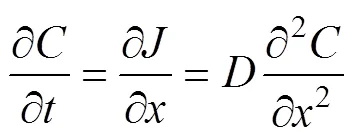
公式(2)表示自由扩散条件下, 溶质浓度随时间变化受浓度梯度控制, 扩散系数可以通过不同的理论与经验公式表示。在忽略溶剂与溶质相互作用的情况下,可以表示为(Einstein, 1906):

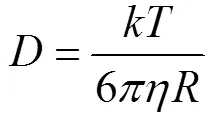
式中:为玻耳兹曼常数;为温度;为动力粘滞系数;为粒子半径。该理论认为扩散系数主要受到环境温度的控制, 不同物质之间的差异在于其粒子半径不同, 因此在这个理论下单个同位素体之间的扩散系数没有差别也不会产生同位素分馏。扩散系数的另外一种经典数学表述为(Alder et al., 1974):

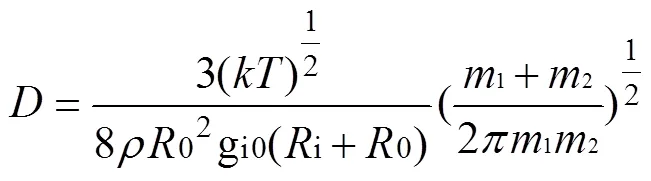
式中:1、2分别为溶质与溶剂的质量;为系统密度;i、0分别为溶质和溶剂的粒子半径; gi0(i+0)指溶剂溶质接触点处溶剂的径向分布函数的值。通过公式可见, 质量差异会影响同位素体在水溶液中的扩散系数, 从而导致同位素分馏。

2 扩散同位素分馏实验研究进展

模拟实验设计的发展和定量分析技术的进步, 丰富了水相扩散模拟实验的研究对象, 更多气体分子和有机化合物的扩散同位素分馏相关的基础参数才得以确定。

达西尺度的扩散同位素分馏实验是开展最为广泛的一类实验。截至目前, 达西尺度下的水溶液扩散同位素分馏研究涉及: 主要离子(K+, Na+, Ca2+, Mg2+, Ba2+, Fe2+, Fe3+, Zn2+, Li+, Cl–和Br–)(Kunze and Fuoss, 1962; Pikal, 1972; Rodushkin et al., 2004; Schloemer and Krooss, 2004; Richter et al., 2006; Eggenkamp and Coleman, 2009; Bourg et al., 2010; van Zuilen et al., 2016)、稀有气体(He, Ne, Ar, Kr和Xe)(Tempest and Emerson, 2013; Tyroller et al., 2014; Tyroller et al., 2018)、部分含碳温室气体的碳同位素(二氧化碳、甲烷和乙烷)(Oleary, 1984; Jähne et al., 1987)、部分地下水有机污染物的碳同位素(1,2-二氯乙烷和三氯乙烯)和氯同位素(顺二氯乙烯、1,2-二氯乙烷和三氯乙烷)(Jin et al., 2014; Wanner and Hunkeler, 2015)以及代表性的有机同位素标记物(异丙醇、叔丁醇、苯和甲苯)(LaBolle et al., 2008; Jin et al., 2014; Rolle and Jin, 2017)。

2.1 实验目的与要求

达西尺度下, 水相扩散模拟实验的目的是在单一扩散过程制约的条件下, 模拟溶质的扩散并定量分析溶质浓度与同位素比值的变化, 进而基于Fick’s定律求得单个同位素体的扩散系数。为此, 要求实验系统: ①尽可能封闭, 排除溶质和溶剂的蒸发流失; ②水体不受机械运动影响以避免非扩散作用造成的溶质迁移; ③无生物或化学转化过程; ④温度恒定; ⑤系统可以建立较大浓度梯度以保证扩散的进行。另外, 自由扩散是各向同性的过程, 扩散模型只需监测一个方向上目标物相关信号的时空变化便能获取相关参数。

2.2 实验对象与方法

早期, 扩散模拟实验的研究对象为常见水溶性离子。Lind and Fuoss (1961)和Kunze and Fuoss (1962)利用三通扩散槽模拟了Li+和K+等离子的扩散, 通过定量分析不同槽室中溶液密度随时间的变化, 从而计算出Li+及其同位素的扩散系数。Pikal (1972)与Oleary et al. (1984)引进隔膜扩散槽用于模拟扩散过程, 通过分析交换膜两端槽室中溶质的浓度变化, 来研究Na+以及溶解性较高的CO2的扩散同位素分馏。Rodushkin et al. (2004)分别用多孔介质和玻璃毛细管设计了两种简单的扩散实验装置来研究稀硝酸溶液中Fe离子和Zn离子的扩散过程, 系统简单且能改变溶液其他参数(如pH值和氧化还原电位等), 但是此系统对稳定性要求较高。Richter et al. (2006)和Bourg et al. (2010) 采用经典的Graham渗透实验, 通过毛细管中高浓度溶液向外部容器扩散的模拟实验系统, 定量分析了K+, Ca2+, Mg2+和Cl–等离子的扩散系数与同位素分馏。该系统简单易搭建, 但要求外部容器体积足够大且溶质混合速率远大于扩散速率(即外部容器中溶质浓度较低且分布均匀), 仅适用于研究水溶性高且化学性质稳定的目标物。上述实验都成功地模拟了离子的自由扩散过程, 获取了不同离子的扩散同位素分馏系数, 并初步认识了扩散同位素分馏的程度, 也为扩散同位素分馏机理的研究与实际应用提供了基础数据。

与上述实验方法类似, 一部分研究通过搭建低流速的实验系统模拟了有机化合物在水溶液中的扩散。LaBolle (2008)利用折射指标分析方法研究了溶解度较高的氘代或非氘代异丙醇和氘代或非氘代叔丁醇的扩散系数。Wanner et al. (2015)在非严格静水条件下的多孔介质中布置了扩散源,对1,2-二氯乙烷和三氯乙烷的碳和氯扩散同位素分馏效应进行了研究。然而, 由于有机物低极性和挥发性等特点, 要求实验系统具有较高的封闭性, 另外还要保证实验系统中机械混合等水动力学条件不影响溶质浓度与同位素分布, 这些因素导致针对有机物的模拟实验系统设计要求较高, 相关研究进展比较缓慢。为解决这个问题, 以水凝胶为介质的扩散模拟实验(Davison et al., 1994)被逐步引入。水凝胶扩散模拟实验是通过加入少量凝胶试剂, 搭建固态介质扩散实验系统来模拟溶质的扩散过程, 从而在保证溶剂性质基本不变的情况下, 满足目标物的同位素定量分析要求, 同时能够排除其他物理过程对实验过程的干扰。这类设计最早被用来模拟Ba2+, Cl–和Br–的扩散过程并可通过计算得到相应的扩散同位素分馏系数(Eggenkamp and Coleman, 2009; van Zuilen et al., 2016), 也被用于一系列微溶有机物如全氘代或非氘代的苯、甲苯、乙苯、1,2-二氯乙烯、三氯乙烯和顺二氯乙烯的C, H, Cl扩散同位素分馏研究(Jin et al., 2014; Rolle and Jin, 2017)。相比其他传统方法, 凝胶介质扩散模拟实验有其独特的优势: ①可以完全排除溶剂机械运动对溶质运移分布的影响, 实验配置与操作更加方便灵活; ②对于低溶解度的组分(低极性有机物和稀有气体等)而言, 更容易满足仪器分析的检出限; ③可以在空间上实现连续观测, 更直观了解溶质浓度与同位素组成时空变化, 增加了数据采集量。但是, 该实验系统的样品为固态样品, 定量分析时需要采用合理的前处理与化学分析技术。

为了研究难溶于水的温室气体和稀有气体分子的扩散同位素分馏, 需要定制密封性更好的模拟实验系统, 并结合在线分析技术进行研究。Zhang and Krooss (2001)和Schloemer and Krooss (2004)使用三轴流动扩散槽, 对甲烷、乙烷的水相自由扩散过程进行了模拟和研究, 通过配置高压系统, 增加气体在水溶液中的分配系数, 在线分析多孔介质(水饱和岩石样品)水相系统中气体的浓度变化与碳同位素分馏。Tempest and Emerson (2013)使用大体积水相(总计17.1 L)实验装置, 对氖气、氩气的扩散同位素分馏进行了模拟实验研究。Tyroller et al. (2014, 2018)则设计了一个气相–凝胶–气相的扩散模拟系统, 提供恒定的气相源(温度、流速和组成等保持不变), 在线监测被凝胶介质分隔开且初始目标物分压为0的槽室中稀有气体元素的同位素组成随时间的变化, 从而定量分析了氩气、氪气和氙气的稳定同位素分馏效应。

2.3 实验结果与讨论

基于上述结果, 轻同位素及同位素体的扩散系数L比重同位素及同位素体的扩散系数H大,H/L值小于1(除氘代与非氘代苯的结果以外), 表明绝大多数溶质的轻同位素会随着自由扩散的进行而富集, 且同位素分馏的程度随溶质类型的变化产生明显的差异。

为了进一步探究扩散同位素分馏效应, Pikal (1972)就扩散系数与溶质质量的关系进行了研究, 发现水中单个同位素体扩散系数的比值与质量的比值的关系并不满足公式(4)的推导结果, 并得出公式(5), 而Worch (1993)通过气体自由扩散经验公式推导得出公式(6):

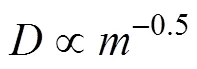
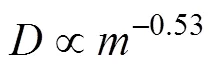
通过进一步研究, Richter et al. (2006); Bourg and Sposito (2007)和Bourg et al. (2010)基于K+, Na+, Ca2+, Mg2+和Cl−离子扩散模拟实验的数据, 参考Craig and Gordon (1965)的研究, 引入了扩散同位素分馏的质量相关系数“值”, 得出公式(7)来对比解析不同溶质扩散系数的差异。

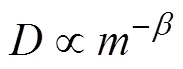
如图1、2所示, 无机离子的扩散同位素分馏质量相关系数的变化范围相对较小(=0.000～0.042)且不同实验系统下的结果相近, 都与理想气体自由扩散体条件下的理论值(=0.5)相差甚远, 可以认为其扩散过程受水的制约较大而质量相关性相对较小。惰性气体的值变化范围较大, 为0.037～0.508, 实验结果显示惰性气体既有类似无机离子的较低的值(Ne、Xe), 也有接近理想气体自由扩散的高值, 且由于惰性气体溶解度低, 对实验系统的要求更高, 导致不同研究得到的结果存在争议(Ne、Ar)。温室气体(二氧化碳, 甲烷, 乙烷)碳同位素的值很接近, 为0.031～0.039。有机物的相关研究比较缺乏, 其中氯代烷烃类物质值的变化区间相对较窄, 为0.023～0.088, 并且同种物质中氯同位素与碳同位素的值存在差异, 可以认为不同元素同位素对分子在水相中的扩散影响有所不同, 这可能跟同位素体本身的性质及同位素在分子中的分布位置相关。而同位素标记物的值存在显著的差异(−0.247～0.463), 其中氘代苯或非氘代苯的值甚至小于0(反向同位素分馏, 即重同位素异数体的扩散系数大于轻同位素异数体的扩散系数)。一系列质量相关性的研究表明, 不同组分在水相中的扩散都不同程度地偏离了理想气体自由扩散条件下的结果, 即值皆小于理论值(0.5), 说明各个组分在水相中的扩散过程都不同程度地“受阻”, 即“自由扩散”的程度有所差异。

由表1和图3可见, 对于二氧化碳和有机化合物, 不同组分碳同位素的相对质量差与值呈现出一定程度的正相关, 质量相关性较强(值较大)的组分的扩散同位素分馏更容易被同位素相对质量差等质量相关参数所制约。目前为止, 由于自然同位素丰度有机化合物的相关实验研究还比较欠缺, 仅有部分地下水有机污染物的数据报道(氯代烷烃类物质), 难以总结出其他元素单体同位素的扩散分馏规律。此外, 在现有同位素标记物的研究中, 所选取的研究对象(醇类物质以及苯系物)分子结构与性质存在较大的差异, 较难进行对比分析, 并且多数实验采用了氘标记物。因此, 其他元素稳定同位素标记物的扩散同位素分馏研究仍缺乏基础数据。

图1 无机离子和气体水相扩散模拟实验结果总结的扩散同位素分馏系数的质量相关系数(β值)(据Wanner and Hunkeler, 2019a)

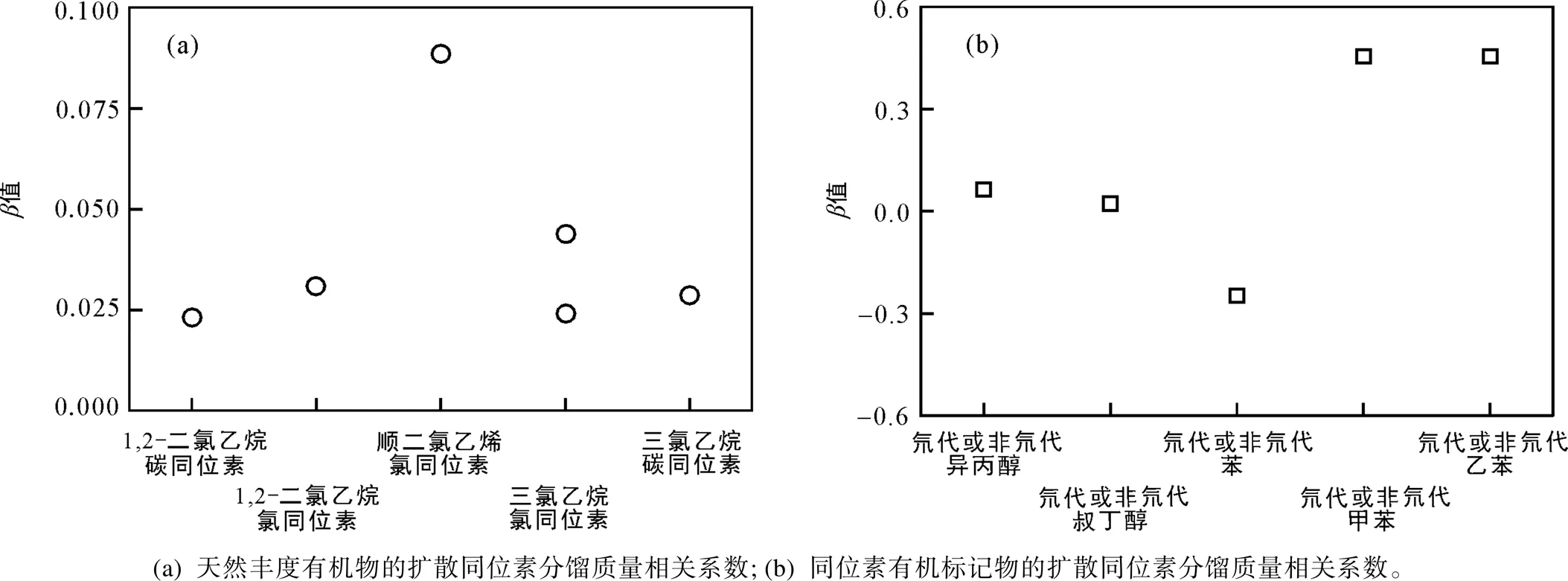
图2 有机化合物物扩散模拟实验结果和相关综述总结的扩散同位素分馏系数的质量相关系数值(β值)(据Wanner and Hunkeler, 2019a)

表1 有机化合物及气体的扩散系数与同位素质量相关参数的总结

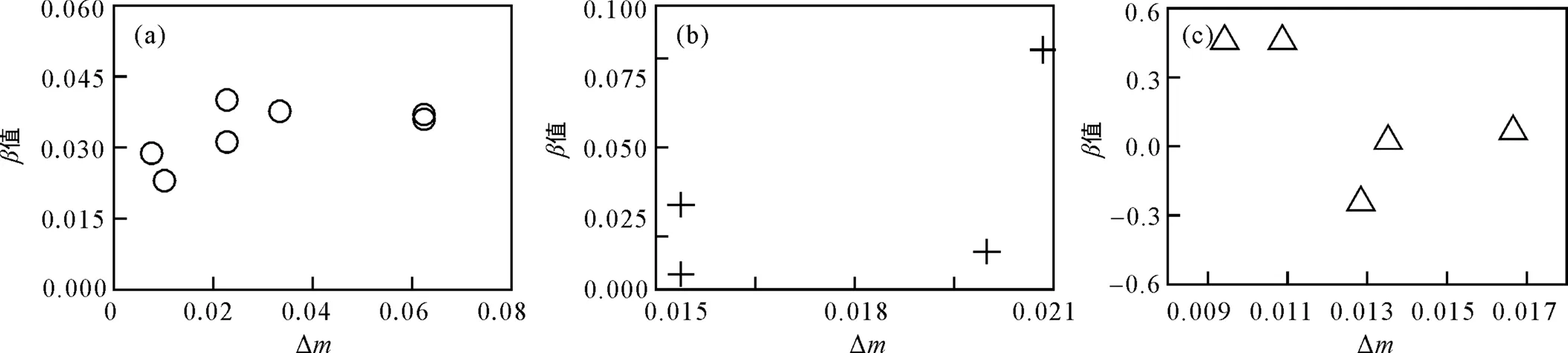
图3 δ13C (a)、δ37Cl (b)和δD (c)相对质量差与质量相关系数β值散点图

迄今为止, 水溶液中溶质的扩散同位素分馏研究主要针对无机离子与稀有气体, 而针对单体溶质的相关研究数据相对较少, 单体溶质的自由扩散过程对单体同位素信号模型模拟研究的影响尚不明确, 数据的匮乏也限制了对扩散同位素分馏机理的深入认识, 因此相关的模拟实验与对比分析研究亟待加强。

2.4 数据分析总结

一系列的研究基于扩散同位素分馏的质量相关系数值, 对扩散同位素分馏的机理进行了探索。结合早期的离子同位素模拟实验结果, Richter et al. (2006)认为, 由于水动力摩擦与溶质半径成正比, 微观尺度下, 不同极性离子与水分子结合的数量会影响离子在水溶液中的有效体积效应, 导致不同离子值的差异。该理论指出离子在水溶液中是不完全自由的, 需要考虑与水分子结合后的体积效应的影响。对于值较高的离子, 依据该理论, 结合合理数量的水膜水分子便可解释通过模拟实验得到的值, 如Li+12H2O, Cl+37H2O。但是, 该理论尚不能完全解释值较低的离子的扩散同位素分馏现象。该理论考虑到极性物质在水溶液中物化性质的变异, 一定程度地解释了水相中不同组分扩散同位素分馏效应的差异。有人则引入分子动力学模型(Molecular dynamic simulation, MDS)(Bourg and Sposito, 2007; Bourg et al., 2010), 通过计算机模拟研究微观尺度下单个分子或离子在刚性、不可极化的水分子群中的运移, 来模拟扩散过程和测定扩散系数, 并结合实验数据验证了MDS模拟Na+, K+, Cs+, Ca2+, Li+, Li–, Cl–和Mg2+等离子扩散的结果。de Magalhães et al. (2017)用MDS拟合了一系列稀有气体的扩散同位素分馏效应。Wanner and Hunkeler (2019b)也用分子动力学模型模拟了有机化合物的扩散过程, 并重现了1,2-二氯乙烷和三氯乙烷的碳、氯同位素的模拟实验结果。以上研究显示MDS是研究扩散同位素分馏机理和制约因素的有力工具。

3 水相系统扩散同位素分馏研究的现状与展望

在水动力条件较为迟缓的多孔介质水相系统中, 扩散、弥散、吸附和解吸附等物理过程控制着溶质的时空分布, 同时也可以影响溶质的稳定同位素信号的分馏演化, 其中扩散系数是间接影响弥散等过程的基础参数, 因此, 对溶质扩散过程的相关研究十分重要。这意味着对地下水、沉积物孔隙水进行溶质的源解析和迁移转化过程示踪时, 不仅要考虑化学及生物转化等因素, 也需要考虑包括扩散等其他“同位素敏感”的物理过程影响下的耦合同位素分馏效应, 才能推断出更准确和可靠的结论。

目前为止, 水溶液中溶质的扩散同位素分馏研究相对滞后, 缺乏相关数据。多数研究针对无机离子与惰性气体, 而对于环境单体的稳定同位素仍缺少系统研究。主要原因在于各类环境单体的物理化学性质的差异, 从而加大了模拟实验与定量分析的难度。同时, 有机化合物由于元素组成及分子结构不同, 造成不同单体在水溶液中的物化性质差异较大, 因此较难对扩散同位素分馏机理进行解析。

综上, 我们认为今后的研究应着重从以下三个方面开展:

(1) 加强具有重要环境地球化学意义单体的扩散同位素分馏研究。首先, 应基于已有的相关研究进行数据补充, 如苯系物、氯代烷烃、醇类物质等。对比分析相同类型有机物的研究结果有助于总结分子质量、碳数等因素对同位素分馏效应的影响, 也有助于了解不同类型有机物的扩散同位素分馏参数的变化范围以及质量相关性。其次, 应进一步研究更复杂的有机物或同位素标记物, 如离子型有机物、双同位素标记物等。对复杂单体的研究, 有利于了解分子结构、分子性质和同位素类型等不同因素对扩散同位素分馏的影响, 以此深入探索分馏机理。

(2) 基于研究对象在水相中的物化性质, 针对性地搭建实验及分析系统, 模拟并测定扩散过程中溶质的浓度以及同位素组成的时空演化来确定扩散系数等基础参数, 仍是扩散同位素分馏研究的基本思路和方法。此外, MDS相关模型越来越多地被用于计算机模拟分子尺度下离子、惰性气体以及部分有机物的扩散过程, 该方法被证明在测算与定量分析扩散相关系数方面具有优势和潜力, 但仍需要结合更多实验数据(如同位素标记有机物)进一步验证模型的可行性和适用范围。

(3) 加强扩散同位素分馏研究, 很大部分是出于地学领域研究的实际需求(LaBolle et al., 2008; Eggenkamp and Coleman, 2009; Jin et al., 2014)。今后的研究仍需聚焦扩散同位素分馏机理、多过程耦合同位素效应等问题, 进一步开展更细致的实验和模型研究, 以期深入地理解影响溶质扩散同位素分馏的主要因素, 进而更准确地同位素分馏程度以及示踪相关过程。这些工作将有助于更完整、更准确地解析地下水、孔隙水等真实环境中溶质的同位素观测数据, 从而提高同位素信号解析的准确性。最终,基于溶质的稳定同位素信号预测水文地球化学系统中溶质的来源、分布、迁移和转化。

Alder B J, Alley W E, Dymond J H. 1974. Studies in molecular dynamics. XIV. Mass and size dependence of the binary diffusion coefficient., 61(4): 1415–1420.

Bourg I C, Richter F M, Christensen J N, Sposito G. 2010. Isotopic mass dependence of metal cation diffusion coefficients in liquid water., 74(8): 2249–2256.

Bourg I C, Sposito G. 2007. Molecular dynamics simulations of kinetic isotope fractionation during the diffusion of ionic species in liquid water., 71(23): 5583–5589.

Craig H, Gordon L. 1965. Deuterium and oxygen 18 variationin the ocean and marine atmosphere // Tongiorgi E. StableIsotopes in Oceanographic Studies and Paleotemperatures: 9–130.

Davison W, Zhang H, Grime G W. 1994. Performance characteristics of gel probes used for measuring the chemistry of pore waters., 28(9): 1623–1632.

de Magalhães H P, Brennwalda M S, Kipfer R. 2017. Diverging effects of isotopic fractionation upon molecular diffusion of noble gases in water: Mechanistic insights through ab initio molecular dynamics simulations., 19: 405–413.

Eggenkamp H G M, Coleman M L. 2009. The effect of aqueous diffusion on the fractionation of chlorine and bromine stable isotopes., 73(12): 3539–3548.

Einstein A. 1906. Über die von der molekularkinetischen theorie der wärme geforderte bewegung von in ruhenden flüssigkeiten suspendierten teilchen einstein., 17: 549–560.

Fick A. 1855. Über Diffusion., 170: 59–86.

Hofstetter T B, Schwarzenbach R P, Bernasconi S M. 2008. Assessing transformation processes of organic compoundsusing stable isotope fractionation., 42(21): 7737–7743.

Jähne B, Heinz G, Dietrich W. 1987. Measurement of the diffusion coefficients of sparingly soluble gases in water., 92(C10): 10767–10776.

Jin B, Rolle M, Li T, Haderlein S B. 2014. Diffusive fractionation of BTEX and chlorinated ethenes in aqueous solution: Quantification of spatial isotope gradients., 48(11): 6141–6150.

Kunze R W, Fuoss R M. 1962. Conductance of alkali halides. 3. Isotopic lithium chlorides., 66(5): 930–931.

LaBolle E M, Fogg G E, Eweis J B, Gravner J, Leaist D G. 2008. Isotopic fractionation by diffusion in groundwater., 44(7): 344–349.

Lind J E, Fuoss R M. 1961. Conductance of the Alkali Halides. I. Potassium chloride in dioxane-water mixtures., 65(6): 999–1004.

Oleary M H. 1984. Measurement of the isotope fractionation associated with diffusion of carbon-dioxide in aqeous- solution., 88(4): 823–825.

Pikal M J. 1972. Isotope effect in tracer diffusion. Comparison of the diffusion coefficients of 24Na+and 22Na+in aqueous electrolytes., 76(21): 3038–3040.

Richter F M, Mendybaev R A, Christensen J N, Hutcheon I D, Williams R W, Sturchio N C, Beloso A D. 2006. Kinetic isotopic fractionation during diffusion of ionic species in water., 70(2): 277–289.

Rodushkin I, Stenberg A, Andren H, Malinovsky D, Baxter D C. 2004. Isotopic fractionation during diffusion of transition metal ions in solution., 76(7): 2148–2151.

Rolle M, Jin B A. 2017. Normal and inverse diffusive isotope fractionation of deuterated toluene and benzene in aqueous systems., 4(7): 298–304.

Schloemer S, Krooss B M. 2004. Molecular transport of methane, ethane and nitrogen and the influence of diffusion on the chemical and isotopic composition of natural gas accumulations., 4(1): 81–108.

Tempest K E, Emerson S. 2013. Kinetic isotopic fractionation of argon and neon during air-water gas transfer., 153: 39–47.

Tyroller L, Brennwald M S, Busemann H, Maden C, Baur H, Kipfer R. 2018. Negligible fractionation of Kr and Xe isotopes by molecular diffusion in water., 492: 73–78.

Tyroller L, Brennwald M S, Mächler L, Livingstone D M, Kipfer R. 2014. Fractionation of Ne and Ar isotopes by molecular diffusion in water., 136: 60–66.

van Zuilen K, Müller T, Nägler T F, Dietzel M, Küsters T. 2016. Experimental determination of barium isotope fractionation during diffusion and adsorption processes at low temperatures., 186: 226–241.

Wanner P, Hunkeler D. 2015. Carbon and chlorine isotopologuefractionation of chlorinated hydrocarbons during diffusion in water and low permeability sediments., 157: 198–212.

Wanner P, Hunkeler D. 2019. Isotope fractionation due to aqueous phase diffusion—What do diffusion models and experiments tell?—A review., 219: 1032–1043.

Wanner P, Hunkeler D. 2019. Molecular dynamic simulations of carbon and chlorine isotopologue fractionation of chlorohydrocarbons during diffusion in liquid water., 6(11): 681–685.

Worch E. 1993. Eine neue gleichung zur berechnung von diffusionskoeffizienten gelöster stoffe., 81: 289–297.

Zhang T W, Krooss B M. 2001. Experimental investigation on the carbon isotope fractionation of methane during gas migration by diffusion through sedimentary rocks at elevated temperature and pressure., 65(16): 2723–2742.

Diffusion-induced isotope fractionation of solutes in aqueous solution

ZHANG Jiyun1, 2, 3, JIN Biao1, 2, 3*, ZHANG Gan1, 2

(1.State Key Laboratory of Organic Geochemistry, Guangzhou Institute of Geochemistry, Chinese Academy of Sciences, Guangzhou 510640, Guangdong, China; 2. CAS Center for Excellence in Deep Earth Science, Guangzhou 510640, Guagndong, China; 3. University of Chinese Academy of Sciences, Beijing 100049, China)

Stable isotope analysis is a valuable tool for characterizing the composition, origin, transport, and transformation processes of different solutes in aqueous solutions. Understanding various physical and chemical processes, such as diffusion-induced isotope fractionation, is instrumental for the analysis and applications of stable isotopes. Our study demonstrates the fundamental theory of diffusion-induced isotope fractionation. Different experimental protocols for diffusion simulation experiments are summarized, and the corresponding experimental results, including solutes diffusion coefficients and their mass dependence coefficients, are discussed in detail. Moreover, the interpretation of diffusive isotope fractionation for different target solutes is illustrated based on the hydration-shell theory as well as on the results obtained from molecular dynamic simulation (MDS) studies. Finally, an outlook for future research on diffusive isotope fractionation is presented.

aqueous solution; diffusion; isotope fractionation

X142

A

0379-1726(2022)01-0001-08

10.19700/j.0379-1726.2022.01.001

2020-06-14;

2020-09-20

国家自然科学基金项目(41903065)和中国科学院地球科学领域核心关键技术攻关预研项目(282021000003)联合资助。

张霁云(1995–), 男, 博士研究生, 环境地球化学专业。E-mail: zhangjiyun@gig.ac.cn

金彪(1984–), 男, 研究员, 从事水文地球化学研究。E-mail: jinbiao@gig.ac.cn