基于时频图像和高次频谱特征的雷达信号识别

李世通，全大英，唐泽雨，陈赟，汪晓峰，金小萍

研究与开发

基于时频图像和高次频谱特征的雷达信号识别

李世通，全大英，唐泽雨，陈赟，汪晓峰，金小萍

（中国计量大学，浙江 杭州 310018）

针对低信噪比下雷达信号识别准确率较低的问题，提出了一种基于时频图像和高次频谱特征联合的雷达信号识别算法。该算法首先对信号采用Choi-Williams分布（Choi-Williams distribution，CWD）变换获取时频图像，接着对时频图预处理并用灰度共生矩阵（gray level co-occurrence matrix，GLCM）提取纹理特征；然后利用对称Holder系数提取信号的高次频谱特征；再将纹理特征和高次频谱特征构成一组联合特征向量，最后通过支持向量机（support vector machine，SVM）实现雷达信号的分类识别。通过对8种典型雷达信号进行实验，结果表明本算法在信噪比为−8 dB时，不同信号的识别准确率能达到90%以上。

雷达信号识别；高次频谱；Choi-Williams时频分布；支持向量机

0 引言

雷达信号识别是电子侦察系统的关键环节，其目的是对分选后的雷达信号提取特征参数，并自动识别辐射源信号[1]。正确识别雷达信号可以帮助己方对目标雷达的类型、载体、用途、威胁等级的识别，进而影响下一步的作战决策[2]。

随着战场电磁环境日益复杂，仅基于雷达载频、脉冲宽度、脉冲幅度、到达时间和到达角等组成的常规特征参数已不能满足信号识别的要求。雷达信号脉内特征能有效反映信号本质信息[3]并扩展信号识别的参数空间，因此成为雷达辐射源信号识别研究的热点。时频分析法是研究脉内特征的重要方法，能够以时频图像的形式反映信号频率随时间变换的关系。近年来，许多学者利用数字图像处理技术对雷达信号的时频图像进行研究，并取得了显著成果[4]。白航等[5]采用支持向量机对雷达调频和调相信号CWD（Choi-Williams distribution）时频图像的中心矩和伪Zernike矩特征进行分类识别，在信噪比为−3 dB时采用了伪Zernike矩特征的平均识别率为92%。肖祺等[6]利用Harris角点检测和霍夫变换提取信号CWD时频图像的角点和直线特征，在信噪比为−4 dB时实现了对5种雷达调频和调相信号80%以上的识别率，但低信噪比下识别效果欠佳。刘歌等[7]融合了雷达调频和调相信号时频图像的形状和纹理特征，在信噪比5 dB时识别率接近100%，但信号类型缺乏复合调制信号。关欣等[8]定义了信号的次谱并对次谱提取了相像系数。苑军见等[9]利用脉间参数特征并联合对称Holder系数提取的信号高次频谱特征作为特征向量，实现了对4种雷达调频和调相信号的较好识别。然而随着雷达信号和电磁环境的复杂化和多样化，针对低信噪比下多类型调制的雷达辐射源信号的识别精度也有待进一步提高。

针对上述问题，本文基于能够较好反映信号本质信息的时频图像纹理特征和高次频谱特征，提出了一种特征联合的雷达信号识别算法。实验结果表明本算法在低信噪比下对8种典型雷达信号具有较高的识别率。

1 调制信号联合特征提取

基于低截获概率雷达多采用频率调制、相位调制和这两种类型混合的调制方式，本文选择了这三大类调制方式中常用的8种典型雷达信号展开研究。具体包括常规信号（continuous wave，CW）、线性调频（linear frequency modulation，LFM）、二相编码（binary phase shift keying，BPSK）、多相编码（multi-phase shift keying，MPSK）、四相频率编码（four frequency shift keying，4FSK）和LFM/BPSK、LFM/FSK（linear frequency modulation and frequency shift keying）、FSK/BPSK混合调制信号。

1.1 时频图像纹理特征

1.1.1 CWD时频变换

时频分析法是处理非平稳信号的一个重要方法[10]。常见的时频分析法主要有：短时傅里叶变换（short time Fourier transform，STFT）、Wigner-Ville分布（Wigner-Ville distribution，WVD）和CWD等。其中，STFT存在时频聚集性较差的缺点，WVD会产生干扰真实信号特征的交叉项。因此本文采用了具有较好时频分辨率且能有效抑制和消除交叉项的CWD时频分析法。其计算式为：

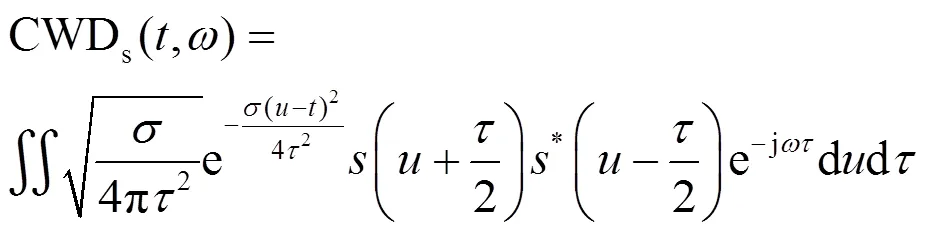
图1给出了信噪比为−8 dB时上述8种信号的CWD时频图像。从图1中可以看出，不同信号的时频图像具有明显的差异，即使在低信噪比下依然能够清晰分辨不同雷达信号，因此可以从信号时频图中提取特征用于信号识别。

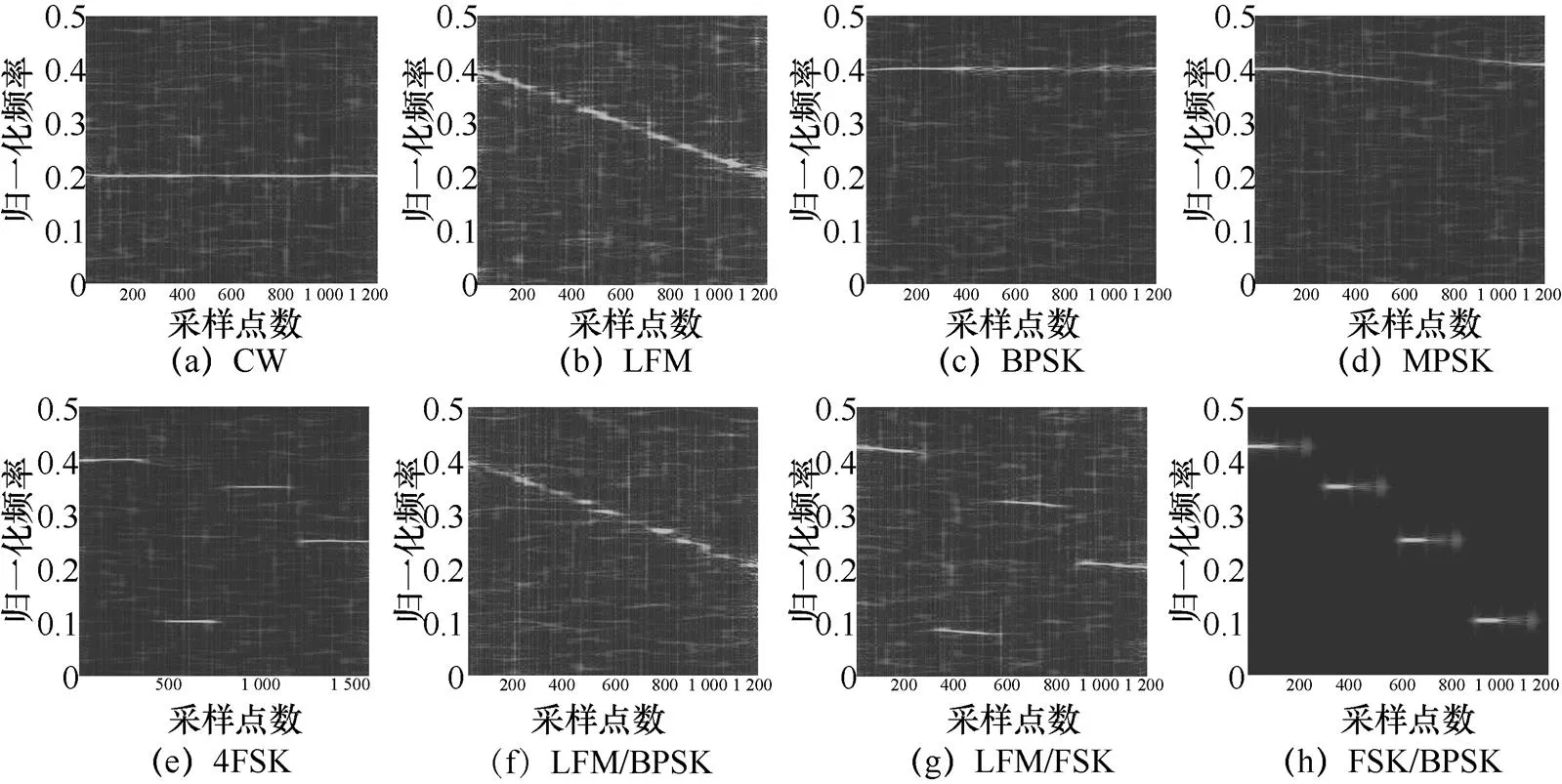
图1 信噪比为−8 dB时8种信号的CWD时频图像

1.1.2 时频图像预处理

由于噪声和时频交叉项的影响，信号时频图存在大量干扰信息[11]，因此，在进行图像特征提取之前，采取图像处理技术对时频图进行预处理，可以有效减少干扰和冗余信息[12]，增强特征提取的有效性。以LFM信号为例，图2为其在信噪比为8 dB时的图像预处理流程。

图2 信噪比为8 dB时的时频图像预处理

预处理过程中，首先将时频图像转换为灰度图，接着对灰度图进行维纳滤波，以便更好地保存图像的边缘和高频细节信息[13]，然后对滤波图进行双三次差值将尺寸缩放到224 dpi×224 dpi，进一步降低数据量。

1.1.3 时频图像特征提取

本文采用灰度共生矩阵（gray level co-occurrence matrix，GLCM）来提取时频图的纹理特征。GLCM统计量包括角二阶矩、熵、对比度、均匀性、相关性、方差、逆差矩和最大相关系数等14种统计量[14]。实际使用中通常选取不相关的角二阶矩、相关性、对比度和均匀性作为GLCM的特征。GLCM的元素用(，)表示，、分别表示不同像素的灰度。

（1）角二阶矩

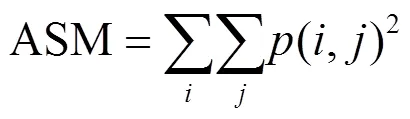
其中，ASM是GLCM各元素的平方和，也称为能量，反映了图像灰度分布均匀程度和纹理粗糙程度。值越小，纹理越细，能量越小。

（2）相关性

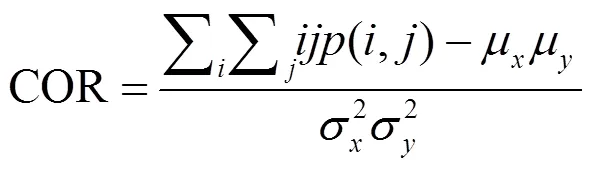
（3）对比度

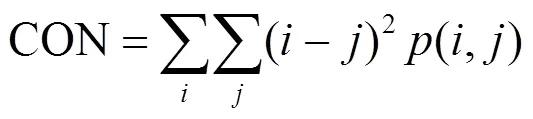
其中，CON反映了图像的清晰度和纹理沟纹深浅的程度。值越小，矩阵中远离对角线的元素值越小，图像越模糊。

（4）均匀性

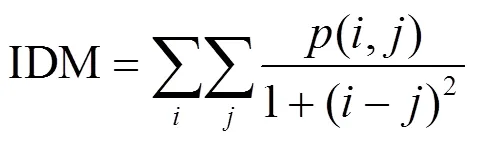
其中，IDM为逆差矩，反映了图像纹理局部变化的大小。值越小，图像局部纹理变换越快。

选取从0°、45°、90°和135°等4个不同方向分别计算GLCM上述4个特征，构成一组16维的特征向量。

1.2 高次频谱特征

高次频谱是指对信号频谱进行次方计算，它可以更好地反映信号在频谱上的细节。利用对称Holder系数对高次频谱进行特征提取，可以获取雷达信号脉内信息。

1.2.1 对称Holder系数定义

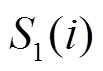
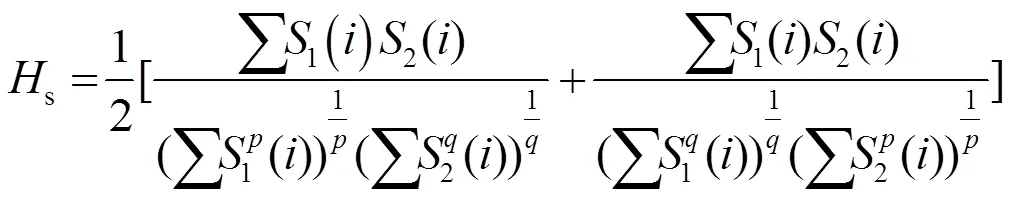
由定义可知，当、都为2时对称Holder系数为相像系数，因此灵活选取、可以获得较好的实验结果。

1.2.2 高次频谱特征提取

首先对信号高次频谱并做归一化处理，得到{()，=1,2,…,}，表示序列长度。为了充分反映两信号之间的相像程度，引入两个基准信号，定义如下。

矩形信号序列为：

三角形信号序列为：

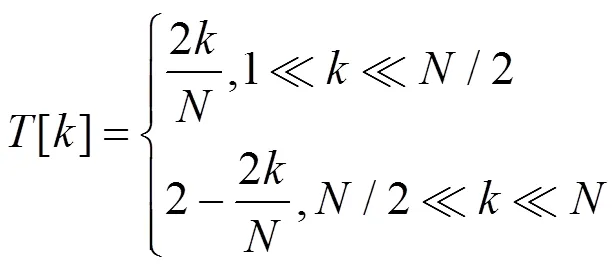
将式（7）和式（8）分别代入式（6）得：

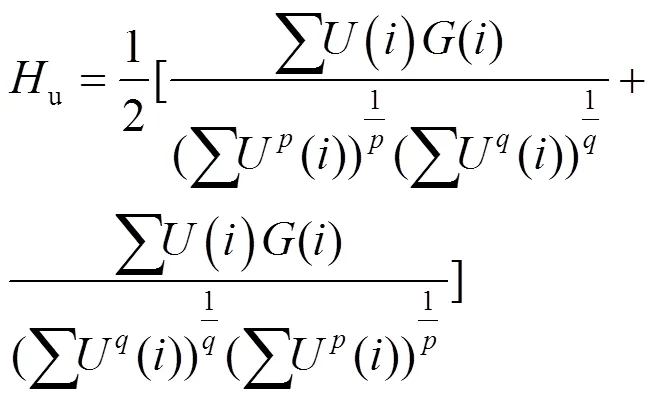
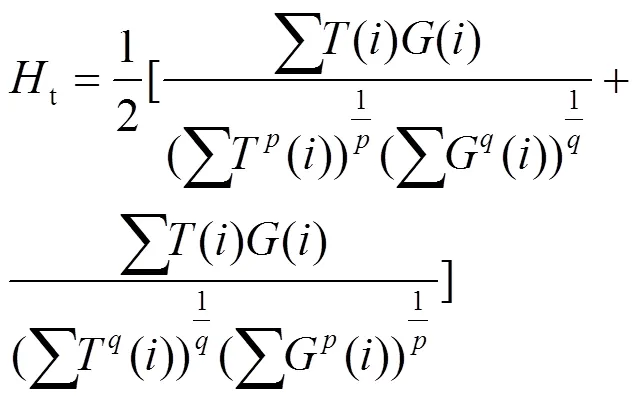
2 信号识别流程

本文基于信号的时频图纹理特征和高次频谱特征，使用SVM分类器对8种典型雷达信号进行识别分类。算法具体步骤如下所示：

步骤1 对接收信号做CWD时频变换得到时频图像，然后对时频图预处理，提取图像纹理特征，得到一组16维特征向量。

步骤2 对接收信号做FFT并归一化，然后计算高次频谱并归一化。

步骤3 利用对称Holder系数提取信号高次频谱特征，得到一组2维特征向量。

步骤4 通过SVM对18维的特征向量识别。

信号识别流程如图3所示。

3 仿真实验分析

选取CW、LFM、BPSK、MPSK、4FSK、LFM/BPSK、LFM/FSK和FSK/BPSK共8种典型雷达信号进行实验。

参数设置如下：采样频率200 MHz，载频20 MHz，脉宽6 μs，带宽40 MHz。其中BPSK采用7位Barker码；MPSK为8位Frank码；4FSK的频率分别为15 MHz、30 MHz、50 MHz和80 MHz。复合调制信号参数设置与上述一致。

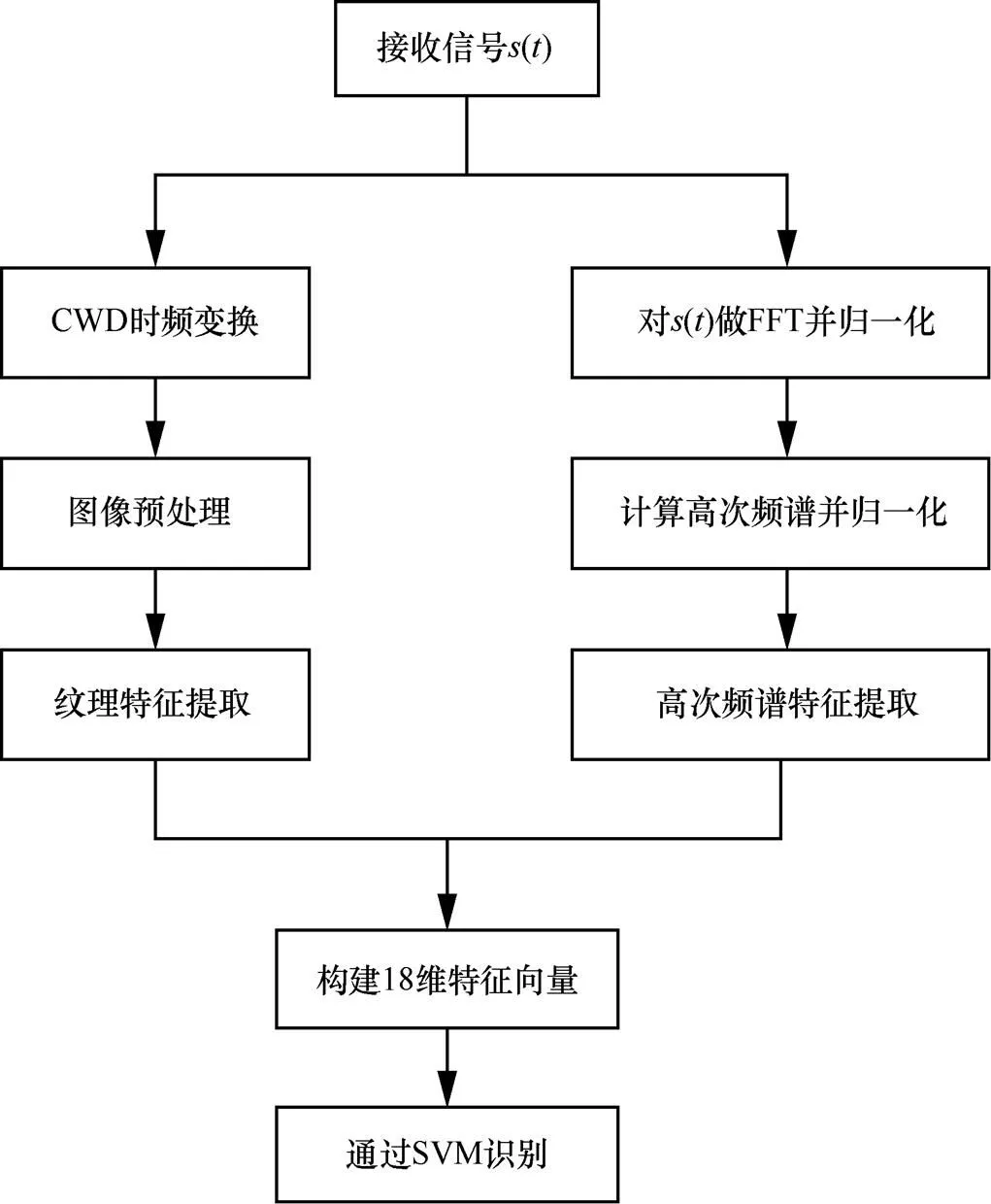
图3 信号识别流程

3.1 高次频谱k值确定

在信噪比8 dB条件下，依次生成LFM、BPSK和LFM/BPSK信号的一次、二次、三次和四次频谱，一次频谱是由信号进行傅里叶变化得到的频谱，二次频谱、三次频谱和四次频谱分别是指对一次频谱进行平方、立方和四次方。结果如图4所示。

从图4可以看出，不同信号频谱具有明显差别，且对频谱进行次方处理后，可以将频谱中细微差异进一步放大，并对噪声产生抑制效果。相比于一次频谱、三次频谱和四次频谱，二次频谱效果最好，不仅能区分信号类别，而且可以避免丢失过多有效信息。

3.2 对称Holder系数值确定

在信噪比为−2 dB的环境下，取9组不同、值。每种信号分别生成100组数据，共构成800组特征向量数据集。因只需要确定、值，不需要构建测试数据集。利用Classification Learner进行训练测试，结果如图5所示。

图4 3种雷达信号高次频谱对比结果

图5 不同参数p值下的训练识别率

由图5可知，经3个不同模型向量机训练识别，为4、为4/3时，效果最好。

3.3 仿真实验与结果分析

选取信噪比范围−12～12 dB，步进2 dB。每一信噪比下各信号分别提取250组特征向量，其中200组用于训练，50组用于测试。分别测试50次结果取平均，结果如图6、图7所示。

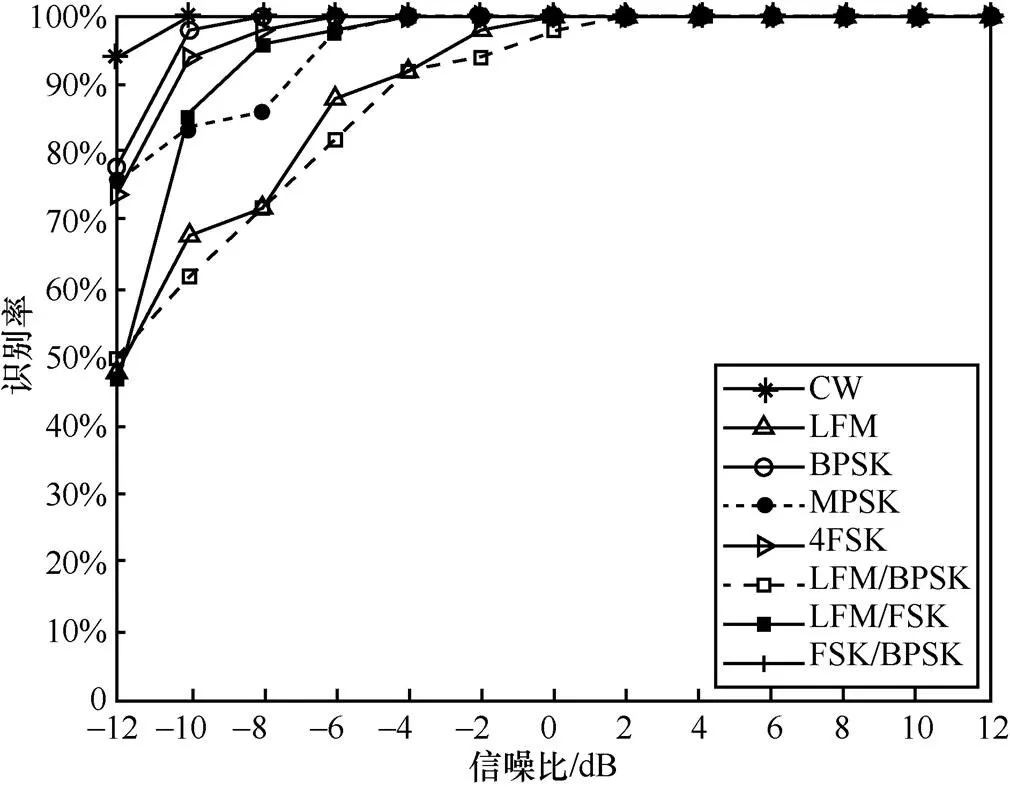
图6 8种信号识别率曲线

从图6可以看出，相较于LFM、LFM/BPSK和LFM/FSK信号，CW、FSK/BPSK信号在低信噪比识别率较高，主要原因是其时频图像不易受噪声影响。

图7 总体识别率曲线

从图7可以看出，各信号总体识别率随信噪比增加而提高。在信噪比为−8 dB时可以达到90%以上的正确率，在信噪比为0 dB时能达到100%的正确率，在信噪比低于−12 dB时依然有70%以上的正确率。

为验证此联合特征具有较好的识别效果，在相同的仿真环境下进行了实验对比。即和单一高次频谱特征、单一纹理特征、文献[16]的相像系数法、文献[17]的分数阶傅里叶变换（fractional Fourier transform，FrFT）法进行实验对比，实验结果如图8所示。

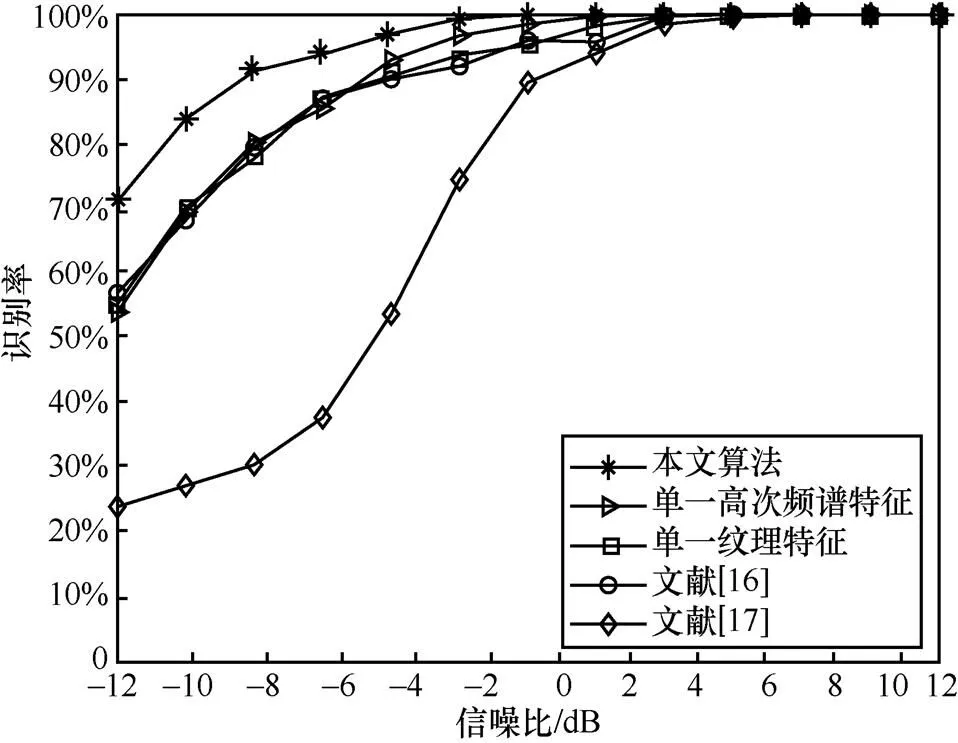
图8 不同算法识别率对比

从图8可以看出，本文联合特征的识别率相比于单一的高次频谱特征和纹理特征具有明显的优势，且高信噪比条件下纹理特征识别率略高于高次频谱特征识别率。FrFT法低信噪比下识别率较低的原因是FrFT波形易受噪声影响，低信噪比下所提特征已不具备较好可分性。

4 结束语

综上所述，针对低信噪比下雷达信号识别准确率较低的问题，提出了一种基于特征联合的识别算法，实现了低信噪比下对多调制类型雷达信号的较好识别，即提取信号CWD时频图纹理特征和高次频谱特征构建联合特征向量，利用SVM分类器实现雷达信号的识别。通过对8种典型雷达信号的验证，结果表明本算法在低信噪比下具有较高的识别率，为不同雷达信号的识别提供了一种可行的方案。

[1] 王俊岭, 黄琰璟. 基于序列关联的参差信号分选算法[J]. 电子与信息学报, 2021, 43(4): 1145-1153.

WANG J L, HUANG Y J. Stagger pulse repetition interval pulse train deinterleaving algorithm based on sequence association[J]. Journal of Electronics & Information Technology, 2021, 43(4): 1145-1153.

[2] 黄颖坤, 金炜东, 葛鹏, 等. 基于多尺度信息熵的雷达辐射源信号识别[J]. 电子与信息学报, 2019, 41(5): 1084-1091.

HUANG Y K, JIN W D, GE P, et al. Radar emitter signal identification based on multi-scale information entropy[J]. Journal of Electronics & Information Technology, 2019, 41(5): 1084-1091.

[3] 周文辉. 基于积分特征的雷达信号调制识别[J]. 舰船电子工程, 2021, 41(1): 46-49.

ZHOU W H. Modulation recognition of radar signal based on integral feature[J]. Ship Electronic Engineering, 2021, 41(1): 46-49.

[4] 孟凡杰, 唐宏, 王义哲, 等. 基于时频图像纹理特征的雷达辐射源信号识别[J]. 弹箭与制导学报, 2017, 37(3): 152-156.

MENG F J, TANG H, WANG Y Z, et al. Radar emitter signal recognition based on texture feature of time-frequency image[J]. Journal of Projectiles, Rockets, Missiles and Guidance, 2017, 37(3): 152-156.

[5] 白航, 赵拥军, 胡德秀, 等. 基于Choi-Williams时频图像特征的雷达辐射源识别[J]. 数据采集与处理, 2012, 27(4): 480-485.

BAI H, ZHAO Y J, HU D X, et al. Radar emitter recognition based on image feature of Choi-Williams time-frequency distribution[J]. Journal of Data Acquisition and Processing, 2012, 27(4): 480-485.

[6] 肖祺, 陈茂洋. 多维时频图像特征组合的电磁辐射源信号识别[J]. 通信技术, 2020, 53(6): 1364-1368.

XIAO Q, CHEN M Y. Electromagnetic emitter signal recognition based on multidimensional time-frequency image feature combination[J]. Communications Technology, 2020, 53(6): 1364-1368.

[7] 刘歌, 张国毅, 汪洪艳. 基于特征融合的雷达信号脉内调制类型识别[J]. 航天电子对抗, 2016, 32(3): 36-41.

LIU G, ZHANG G Y, WANG H Y. Intra-pulse modulation recognition of radar signal based on features fusion[J]. Aerospace Electronic Warfare, 2016, 32(3): 36-41.

[8] 关欣, 朱杭平, 张玉虎. 基于FRFT的雷达辐射源信号特征分析及提取[J]. 探测与控制学报, 2018, 40(2): 71-76.

GUAN X, ZHU H P, ZHANG Y H. Analysis and extraction of radar emitter signal feature based on fractional Fourier transform[J]. Journal of Detection &Control, 2018, 40(2): 71-76.

[9] 苑军见, 陈世文, 刘智鑫, 等. 基于高次频谱对称Holder系数的雷达信号分选方法[J]. 信号处理, 2020, 36(10): 1775-1783.

YUAN J J, CHEN S W, LIU Z X, et al. Radar signal sorting method based on the symmetric holder coefficients of high- order spectrum[J]. Journal of Signal Processing, 2020, 36(10): 1775-1783.

[10] 杨兴宇, 阮怀林. 基于时频图像Zernike矩特征的欺骗干扰识别[J]. 现代雷达, 2018, 40(2): 91-95.

YANG X Y, RUAN H L. A recognition method of deception jamming based on image Zernike moment feature of time- frequency distribution[J]. Modern Radar, 2018, 40(2): 91-95.

[11] 刘燕平, 王冲, 夏海云. 时频分析在激光雷达中的应用进展[J]. 激光与光电子学进展, 2018, 55(12): 68-83.

LIU Y P, WANG C, XIA H Y. Application progress of time-frequency analysis for lidar[J]. Laser & Optoelectronics Progress, 2018, 55(12): 68-83.

[12] 刘歌, 张国毅, 于岩. 基于随机森林的雷达信号脉内调制识别[J]. 电信科学, 2016, 32(5): 69-76.

LIU G, ZHANG G Y, YU Y. Intra-pulse modulation recognition of radar signal based on random forest[J]. Telecommunications Science, 2016, 32(5): 69-76.

[13] WU F, YANG W X, XIAO L M, et al. Adaptive Wiener filter and natural noise to eliminate adversarial perturbation[J]. Electronics, 2020, 9(10): 1634.

[14] 高程程, 惠晓威. 基于灰度共生矩阵的纹理特征提取[J]. 计算机系统应用, 2010, 19(6): 195-198.

GAO C C, HUI X W. GLCM-based texture feature extraction[J]. Computer Systems & Applications, 2010, 19(6): 195-198.

[15] 王海华, 沈晓峰. 基于对称Holder系数的雷达辐射源信号特征分析[J]. 空间电子技术, 2010, 7(3): 55-59.

WANG H H, SHEN X F. Feature analysis of radar emitter signals based on symmetrical holder coefficient[J]. Space Electronic Technology, 2010, 7(3): 55-59.

[16] 陈昌孝, 何明浩, 徐璟, 等. 基于模糊函数相像系数的雷达辐射源信号分选[J]. 电波科学学报, 2014, 29(2): 260-264.

CHEN C X, HE M H, XU J, et al. Radar emitter signal sorting based on resemblance coefficient of ambiguity function[J]. Chinese Journal of Radio Science, 2014, 29(2): 260-264.

[17] 王功明, 陈世文, 黄洁, 等. 基于分数阶Fourier变换的雷达信号分选识别[J]. 计算机应用研究, 2020, 37(S1): 126-128, 131.

WANG G M, CHEN S W, HUANG J, et al. Radar signal sorting and recognition based on fractional Fourier transform[J]. Application Research of Computers, 2020, 37(S1): 126-128, 131.

Time-frequency image and high-order spectrum characteristics based radar signal recognition

LI Shitong, QUAN Daying, TANG Zeyu, CHEN Yun, WANG Xiaofeng, JIN Xiaoping

ChinaJiliang University, Hangzhou 310018, China

Aiming at improving the accuracy of radar signal recognition under a low signal-to-noise ratio, a radar signal recognition algorithm based both on time-frequency image and high-order spectrum feature was proposed. Firstly, the time-frequency image was obtained by Choi-Williams distribution (CWD) transform, based on which the time-frequency image was preprocessed and the texture features were extracted by gray level co-occurrence matrix (GLCM) in sequence. Meanwhile, the symmetrical holder coefficient was used to extract the high-order spectral features of the signal. Then, the texture features and high-order spectrum features were form a new set of joint feature vectors. Finally, with the proposed feature vector the classification and recognition of radar signals were implemented by a support vector machine. The algorithm was verified on the data set with eight typical radar signals. Experimental results show that the recognition accuracy of different radar signals can achieve higher than 90% when the signal-to-noise ratio is −8 dB.

radar signal recognition, high order spectrum, Choi-Williams time frequency distribution, support vector machine

TP393

A

10.11959/j.issn.1000−0801.2022024

2021−05−21；

2022−01−28

浙江省自然科学基金资助项目（No.LQ20F020021）；浙江省电磁波信息技术与计量检测重点实验室开放式项目（No.2019KF0003）

Zhejiang Provincial Natural Science Foundation of China (No.LQ20F020021), Open Project Funding of the Key Laboratory of Electromagnetic Wave Information Technology and Metrology of Zhejiang Province (No.2019KF0003)

李世通（1996− ），男，中国计量大学信息工程学院硕士生，主要研究方向为电子侦察信号处理。

全大英（1979− ），男，中国计量大学副教授、高级工程师，主要研究方向为无线测试系统设计、电子侦察信号处理和智能频谱测量计量。

唐泽雨（1996− ），男，中国计量大学信息工程学院硕士生，主要研究方向为电子侦察信号处理。

陈赟（1997− ），男，中国计量大学信息工程学院硕士生，主要研究方向为电子侦察信号处理。

汪晓锋（1984− ），男，博士，中国计量大学信息工程学院讲师，主要研究方向为复杂数据分析、机器学习及图神经网络。

金小萍（1978− ），女，中国计量大学信息工程学院副教授、硕士生导师，主要研究方向为5G通信、通信检测、物联网通信。