复合换热管过冷沸腾换热实验与关联式评价

刘 萍，秦广进，郭榆生，唐明云，张蔓蔓，汪卫华，黄绍服

(1.安徽理工大学 深部煤矿采动响应与灾害防控国家重点实验室，安徽 淮南 232001；2.安徽理工大学 机械工程学院，安徽 淮南 232001；3.安徽理工大学 安全科学与工程学院，安徽 淮南 232001；4.安徽大学 物质科学与信息技术研究院，安徽 合肥 230061；5.南京航空航天大学 江苏省精密与微细制造技术重点实验室，江苏 南京 210016)

在核聚变反应堆中，偏滤器是直接面向等离子体的重要部件，需承受核聚变反应堆在正常运行和等离子体破裂时的极高热流密度[1-2]。偏滤器承受约10 MW/m2的稳态热流密度[3]，需研究一种高效的强化换热技术，以增强偏滤器在极高热流密度下的运行能力和工质的换热能力。

过冷流动沸腾是指在高热流密度条件下，主流流体温度低于饱和温度，但管内近壁面区域处流体温度已达到产生气泡所需的过热度，具备成核条件，发生过冷沸腾，从而带走大量的热量。同时气泡在流体内的产生、脱离和破裂也会增强管壁面流体的扰动，进一步增强换热特性。从目前的应用现状看，内螺纹肋管和内插扭带管是当前聚变堆主要采用的两种适用于过冷沸腾的强化换热技术。其中内螺纹肋管是通过管道内壁肋片破坏近壁面处边界层底层层流，增强流体在壁面处的扰动和湍流强度，可有效提高边界层区域的换热能力。一些学者[4-9]采用一定形式的螺纹内肋结构来强化过冷沸腾换热，提升换热性能。张小艳等[4]对比了内螺纹管和光管在以非共沸混合制冷剂 R417A为冷却介质时管内的流动沸腾换热特性，实验结果表明，质量流速和干度对流动沸腾换热的影响较大，而热流密度的影响较小，两种内螺纹管的传热系数分别是光管的1.3～2.1和1.5～2.7倍。欧阳新萍等[5]对3种不同内螺纹肋管的传热性能进行了对比研究，结果表明，R22作为冷却介质时测试的3种管型传热效率均高于光管，最高对流换热系数约为光管的2.2倍，在不同流型下较大螺旋角和较多螺纹头数均能强化换热。蔡宏等[6]在低质量流速临界压力条件下，对垂直上升优化内螺纹肋管的传热特性进行了实验研究，结果表明，优化内螺纹肋管这一结构具有较好的传热特性，可有效推迟、避免膜态沸腾的发生。

内插扭带管主要通过扭带实现主流旋转，增强主流流场的湍流脉动强度，同时通过旋转加剧中心冷流向管壁运动，从而增强换热能力，但对壁面边界层内的沸腾换热影响有限。部分学者[10-14]采用管内插入扭带这一方式提高管道的换热特性。朱戈等[10]在单侧加热条件下，对竖直圆管内插入扭带这一结构进行了强化传热特性分析，主要分析了3种主要参数(p、G和q)及扭带结构对沸腾传热特性的影响，对比了几种典型的单相传热关联式，并拟合出了适用于整个过冷沸腾区的传热关联式。Piriyarungrod等[11]研究了扭带的锥角和扰动比的影响，结果表明，换热效果和流动特性随锥角和扰动比的减小而增大；综合换热系数随锥角的增大和扰动比的减小而增大，其中锥角为0.9°、扰动比为3.5时的综合换热系数最大，为1.05。Yan等[12]通过实验研究了在高热流密度下内插扭带管中过冷流动沸腾的换热特性，发现扭带有效增强了充分发展沸腾前的换热，且随着扰动比的降低，换热性能逐渐增强，同时在过冷条件下，提出了改进的对流换热系数新关联式，其误差在±20%以内。

通过叠加或组合不同的强化换热结构可形成多尺度协同强化换热的新技术，更大程度地提升换热性能[15-17]。将内肋强化换热技术与内插扭带管的强化换热技术相结合设计出一种复合换热管，通过内肋结构增强管道壁面附近的湍流强度，内插扭带则提高流场中心区的湍流和旋流特性，达到一种协同效应，同时在流场近壁边界层区和湍流中心区起到协同复合强化换热的作用，对推进更高效偏滤器研制有重要的研究价值和工程意义。大量学者对光管、内螺纹肋管、内插扭带管的换热特性进行了研究[7-9,13-14,18]，但对内螺纹肋管中插扭带的复合换热管的强化换热性能研究较少。

本文拟对光管(PT)、内螺纹肋管(IT)、内插扭带管(TT)和复合换热管(CT)的换热特性和综合性能评价指标进行对比实验研究，并研究扭带扰动比、螺距、压力和质量流速对复合换热管的管内两相流动对流换热系数的影响规律，在实验数据基础上，拟合出适合复合换热管的过冷流动沸腾的努塞尔数关系式。

1 实验系统及试件参数

1.1 实验系统

本实验在中国科学技术大学的多相与多场耦合力学实验室的高热流综合实验平台上进行[19]。高热流综合实验平台原理图和实验测试段实物图分别示于图1、2。实验装置由电子束加热系统、冷却水循环系统、温度压力信号采集系统、多通道数据采集系统、流量计、压力调节器、循环泵和热交换器等组成。采用两种不同涡街流量计测量管道流量，其精度为0.5%，流量范围分别为0.3～5.5 m3/h和1～20 m3/h。热电偶所测温度通过USB-7410远端热电偶采集模块输送到计算机端口显示，采用φ0.5 mm的K型热电偶测量温度。在实验测试段进出口处，设有压力和温度测量点，实验管道中冷却水的温度通过温度变送器来测量，温度变送器的型号为PCT300，量程为0～300 ℃，精度0.5%FS。采用压力变送器测量实验管道进出口压降数值，压力变送器的型号为PCM300H，量程为0～5 MPa，精度为0.5%FS。加热设备为电子束加热系统，为满足加热系统的工作需求，测试段加热过程在真空室中进行，总加热功率为50 kW，真空室工作压力为10-2Pa。

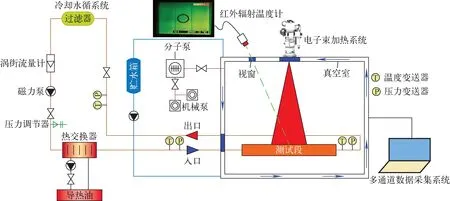
图1 高热流综合实验平台原理图

图2 测试段实物照片

1.2 试件参数

实验选用的复合换热管是在内螺纹肋管内部焊接插入1根扭带来强化换热，复合换热管结构示意图如图3所示。复合换热管水平放置，单面(上水平面)受热流密度，测试管道结构参数列于表1，测试段管长L为130 mm。在测试管靠近热源的一侧开了两排小孔以安装热电偶，每排14列，两排小孔径向距离为2 mm，轴向间隔为5 mm或10 mm。扭带结构示意图如图4所示，内插扭带的厚度δ为0.5 mm。扭带扰动比y和宽度比w的定义如式(1)和(2)所示。

图3 复合换热管结构示意图

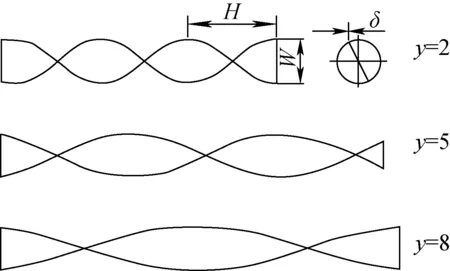
图4 扭带结构示意图

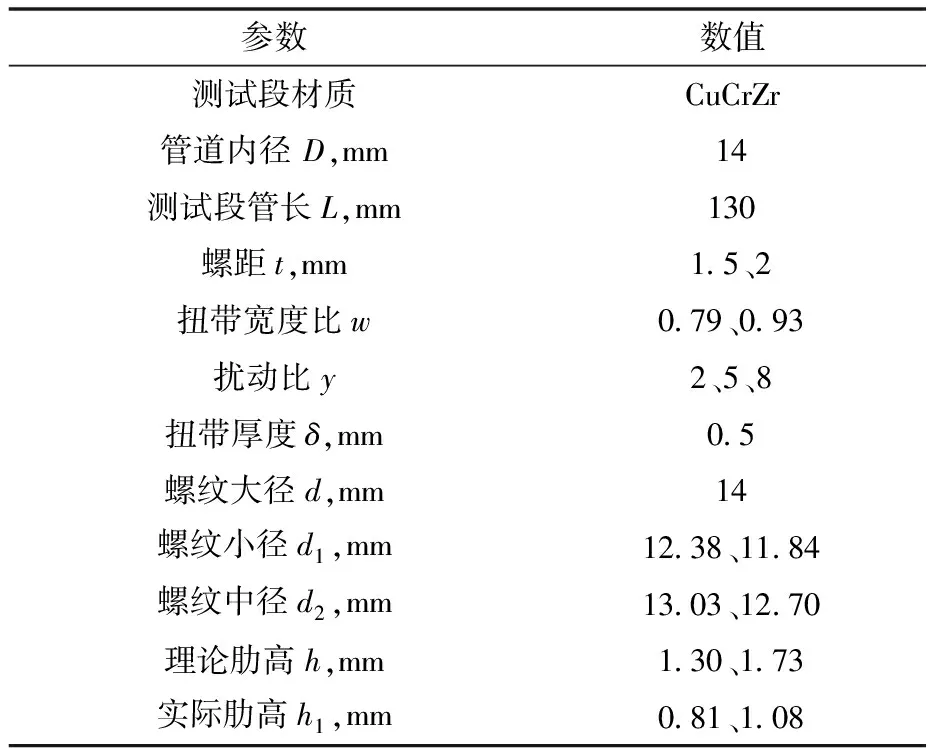
表1 管道结构参数

y=H/D

(1)

w=W/D

(2)

其中：H为50%的扭带扭距，mm；W为扭带的宽度，mm；D为复合换热管的内径，mm。

本实验扭带的扰动比y为2、5、8，扭带的宽度比w为0.79、0.93。图5为复合换热管内螺纹肋的结构示意图，其中内螺纹肋的螺距t为1.5、2 mm。

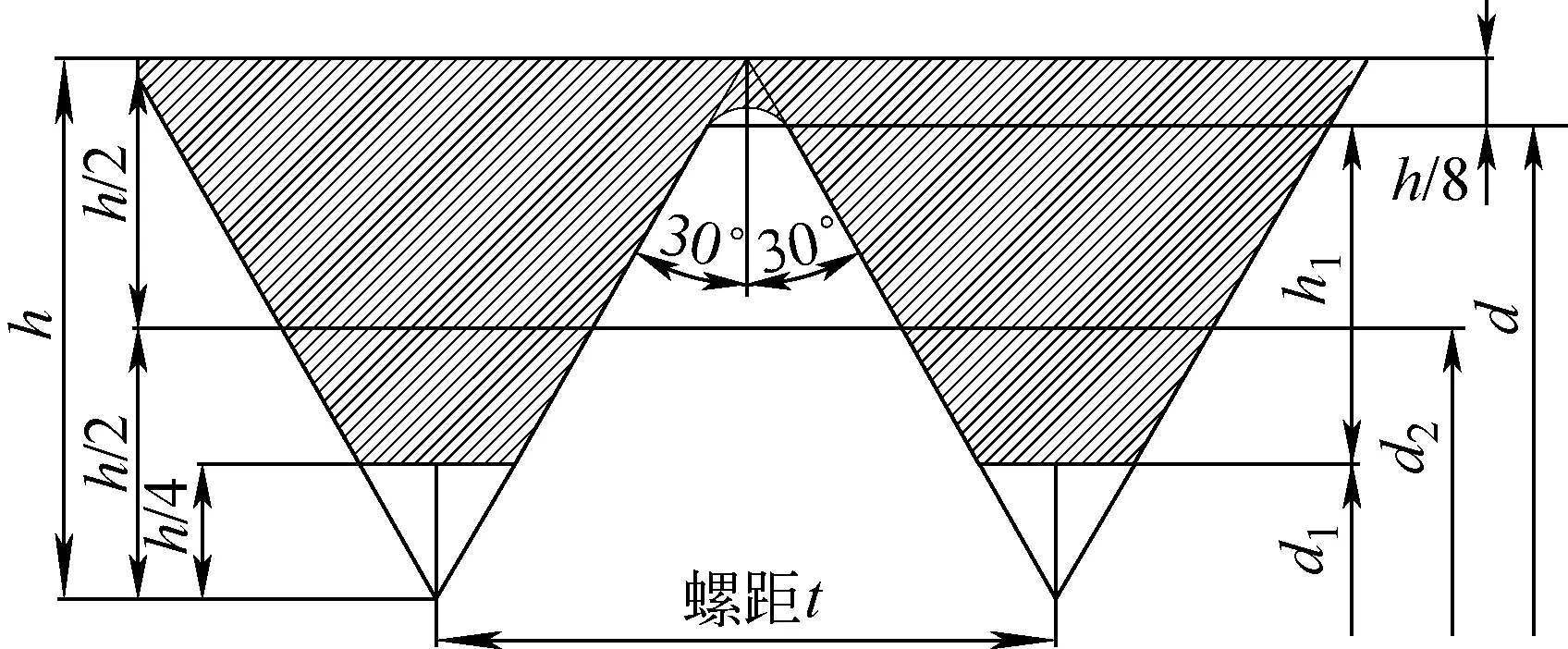
图5 内螺纹肋的结构示意图

2 数据处理及可靠性验证

2.1 数据处理

实验中的水力学参数范围列于表2。每个位置的温度都是稳定测量的平均值，水的热物理性质取自REFPROP_V9.0[20]。

表2 水力学参数范围

将复合换热管道上方固体区域近似为一维导热，其热流密度q(MW/m2)计算公式如下：

(3)

其中：k为CuCrZr热导率，kW/(m·K)；ΔT为同一截面上下热电偶之间的测量温度差，℃；l为同一截面上下热电偶之间的高度差，mm。

对流换热系数h(kW/(m2·K))计算公式如下：

(4)

(5)

其中：Tb为主流流体温度，本实验中取复合换热管进口水温的平均值，℃；Tw为复合换热管内壁温，℃；T2为下热电偶温度，℃；δw,c为下热电偶与复合换热管内壁面之间的径向距离(图3)，本文取1 mm。

复合换热管的等效水力直径Dh,CT为：

(6)

质量流速为：

(7)

其中，M为流体的质量流量，kg/s。

努塞尔数为：

(8)

其中，λ为流体导热系数，kW/(m·K)。

主流流体雷诺数为：

(9)

其中：ρ为流体密度，kg/m3；u为流体平均流速，m/s；μ为流体动力黏度，Pa·s。

进出口压降Δp为：

Δp=pin-pout

(10)

其中：pin为流体进口水压，kPa；pout为流体出口水压，kPa。

流动阻力系数f表示为：

(11)

强化换热管在增强换热能力的同时也使得流体流动阻力特性增加，因此需对其换热能力与流动阻力进行综合考虑，建立便于判断的性能评价方法。本文采用文献[21-22]提出的综合性能评价标准，即：

(12)

其中：PEC为综合性能评价指标；NuT为强化换热管的努塞尔数；Nu0为光管的努塞尔数；fT为强化换热管的流动阻力系数；f0为光管的流动阻力系数。

采用平均绝对误差(MAE)和均方根误差(RMSE)来评估经验公式的预测精度，其中MAE可作为预测精度评估的标准，RMSE则主要反映预测数据的离散程度。MAE和RMSE的计算公式如下：

(13)

RMSE=

(14)

其中：N为数据点个数；Nu(i)cor和Nu(i)exp分别为第i个点的公式预测值和实验值。

采用Kline等[23]的方法进行不确定度分析，依据该方法分别得出热流密度和对流换热系数的不确定度计算公式，如式(15)和(16)所示。

(15)

(16)

复合换热管主要参数的不确定度列于表3。

表3 复合换热管主要参数的不确定度

2.2 数据可靠性验证

正式实验开展前，需对实验系统的稳定性和精度进行相关标定。用光管的管内流动传热做实验标定，将光管在单相对流时的努塞尔数值与Gnielinski[24]公式的理论计算值进行比较。Nu公式如下：

(17)

其中，f为Darcy-Weisbach摩擦因子，可根据文献[24]中公式得到：

f=(1.82lgRe-1.64)-2

(18)

(19)

其中：Re为主流流体雷诺数；Prl和Prw分别为主流流体温度和壁面温度对应的普朗特数。

光管中单相对流换热系数的实验值与公式预测值对比示于图6，通过对比Gnielinski公式与实验测量的对流换热系数可见，整体误差较小，公式预测值和实验值的相对误差在±15%范围内，平均绝对误差MAE为9.24%，均方根误差RMSE为11.58%，实验值与公式预测值较接近，说明该实验测试系统可靠。

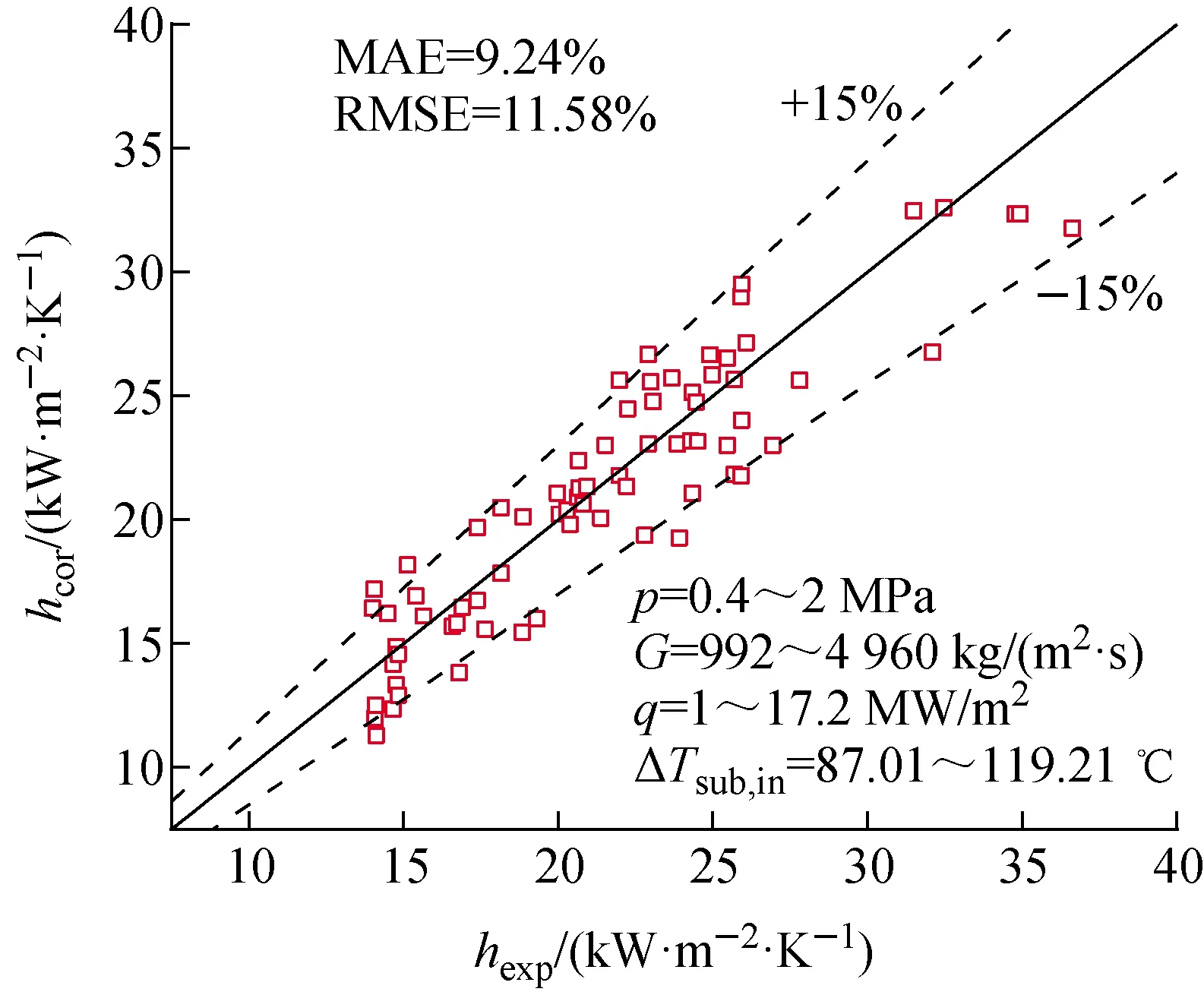
图6 光管单向对流换热系数实验值与公式预测值的比较

3 实验结果及分析

3.1 沸腾曲线

实验用内插扭带管在质量流速4 960 kg/(m2·s)、压力0.4 MPa、入口过冷度102.61 ℃时热流密度从4.55 MW/m2增至16.17 MW/m2工况下的沸腾曲线示于图7。从图7可看出，该曲线主要包含3个区域：单相对流传热区、局部欠热沸腾区和充分发展沸腾区。图7中，A点表示实验起始点，B点表示壁面温度恰好等于流体饱和温度的位置，C点为核态沸腾起始点(ONB点)，D点后发生充分发展沸腾。当壁温增加至C点时，靠近热流密度面的内壁处有足够的过热度，内壁处开始产生微小气泡，为局部欠热沸腾区。如图7a所示，C点之后气泡开始脱离壁面增加流体内部扰动，进而传热系数发生陡增。如图7b所示，C点之后气泡出现，使得壁面换热效果大幅提高，导致壁面过热度上升速度明显降低。故可认为图7中C点为ONB点，C点之前为单相对流传热区。壁温继续增加至D点时，管内流体对流换热系数急剧增加，此时流体进入充分发展沸腾区。而当壁温再进一步增加时，壁面过热度增大，管内发生临界热流密度(CHF)现象，导致传热恶化。本文仅研究CHF发生前复合换热管内的传热增强现象。

图7 沸腾曲线

3.2 管道结构对传热性能的影响

光管、内插扭带管、内螺纹肋管和复合换热管4种不同管道结构对换热特性的影响示于图8。由图8a可见，在壁面温度未达到饱和温度及产生气泡需要的过热度前，管内流场的传热机理为单相液体对流传热，对流换热系数随壁温的变化不明显。当壁温超过产生气泡需要的过热度后，壁面达到气泡成核条件，发生过冷流动沸腾，对流换热系数快速增加。图8b显示，仅在改变质量流速的条件下，对流换热系数随壁面温度的增加而增大，复合换热管的对流换热系数最高，其次为内插扭带管和内螺纹肋管，而光管传热性能最弱。在图8b实验条件范围内，复合换热管的对流换热系数分别较内插扭带管、内螺纹肋管和光管高约5%～98%、99%～102%和179%～184%。

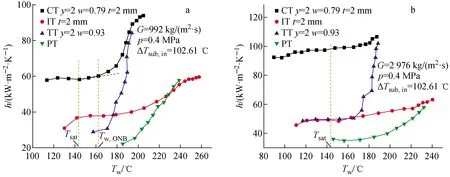
图8 不同管道结构下h随Tw的变化

这一现象可解释如下：1)内插扭带管主要通过旋转加剧中心冷流向热流密度面处管内壁运动，加速了两相流体之间的相互混合。同时，内插扭带还诱发流体产生二次涡流，导致流动过程中流体的黏性影响减小，增强主流流场的湍流脉动强度，从而增加管内流体的轴向速度和离心力，温度梯度增大，换热能力得到增强。2)内螺纹肋管可通过管道内壁肋片破坏近壁面处边界层底层层流，增强流体在壁面处的扰动和湍流强度。内螺纹肋的结构也会使近壁面处流体发生旋转，引起二次流的产生，从而增强近壁面处的湍流强度，致使边界层变薄，有效提高了边界层区域的换热能力。内螺纹肋管还具有毛细提升作用，可在低质量流速时，保证对管壁面的液体供应，使得壁面保持湿润，从而增强换热。复合换热管是将内肋强化换热技术与内插扭带强化换热技术相结合，不仅进一步增加了换热面积，而且在提高管内流场中心区流体湍流和旋流程度的同时，还提高了边界层的扰动，达到协同强化效应，可获得更高效的换热性能。与单独的强化换热技术相比，复合换热管结合了内插扭带和内螺纹肋的对强化换热的双重正推力，极大地增加了复合换热管的换热能力。以上结果表明，与单独的强化传热技术相比，复合换热管的换热能力更优越。

不同管型下PEC随热流密度q的变化示于图9。从图9可看出，相较于内插扭带管和内螺纹肋管，复合换热管具有最大的PEC，这表明内螺纹肋管结合内插扭带这一复合强化结构可有效增强管道内的换热性能。内插扭带管的PEC随热流密度的增大变化不大，但都小于1.0。内螺纹肋管的PEC随热流密度的增大逐渐减小，PEC为0.92～1.26。复合换热管的PEC随热流密度的增加逐渐减小。复合换热管整体PEC在0.91～1.41之间变化，在热流密度小于9.47 MW/m2时，复合换热管的PEC大于1.0，流场中传热效率的增大高于摩擦阻力的提高。在低热流密度时，复合换热管的PEC增加幅度更明显，而随着热流密度的增大，3种管道之间的PEC差距逐渐缩小。在q=6.48 MW/m2时，复合换热管的PEC分别较内螺纹肋管和内插扭带管高约12%和70%，在q=4.38 MW/m2时，复合换热管的PEC出现最高值。

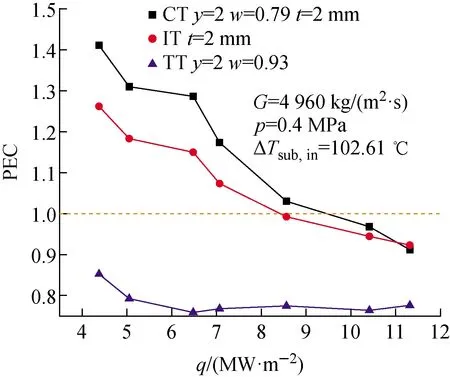
图9 不同管道结构下PEC随q的变化

3.3 复合换热管传热性能的影响因素

3.3.1扰动比 在G=992 kg/(m2·s)、p=2 MPa、ΔTsub,in=102.61 ℃条件下，复合换热管不同扰动比对h的影响规律示于图10。可看出，复合换热管的对流换热系数随扰动比的减小而增大。壁温较小时，扰动比对对流换热系数的影响较明显。随着壁温的增大，扰动比对对流换热系数的影响逐渐减小。在实验热流密度范围内，复合换热管y=2时的对流换热系数较y=5、y=8和光管的分别高约46%～58%、59%～69%和145%～185%。这是因为扭带的周期性变化结构会在复合换热管内增强湍流，扭带的扰动比越小，管壁周围的流体流速越快，主流流场的湍流和旋流强度越大，致使热边界层变薄，边界层处热流体和主流冷流体不断混合。同时管内气泡流动距离更远，气泡流动分离和再附着频率增大，从而使复合换热管的对流换热系数得到增强。

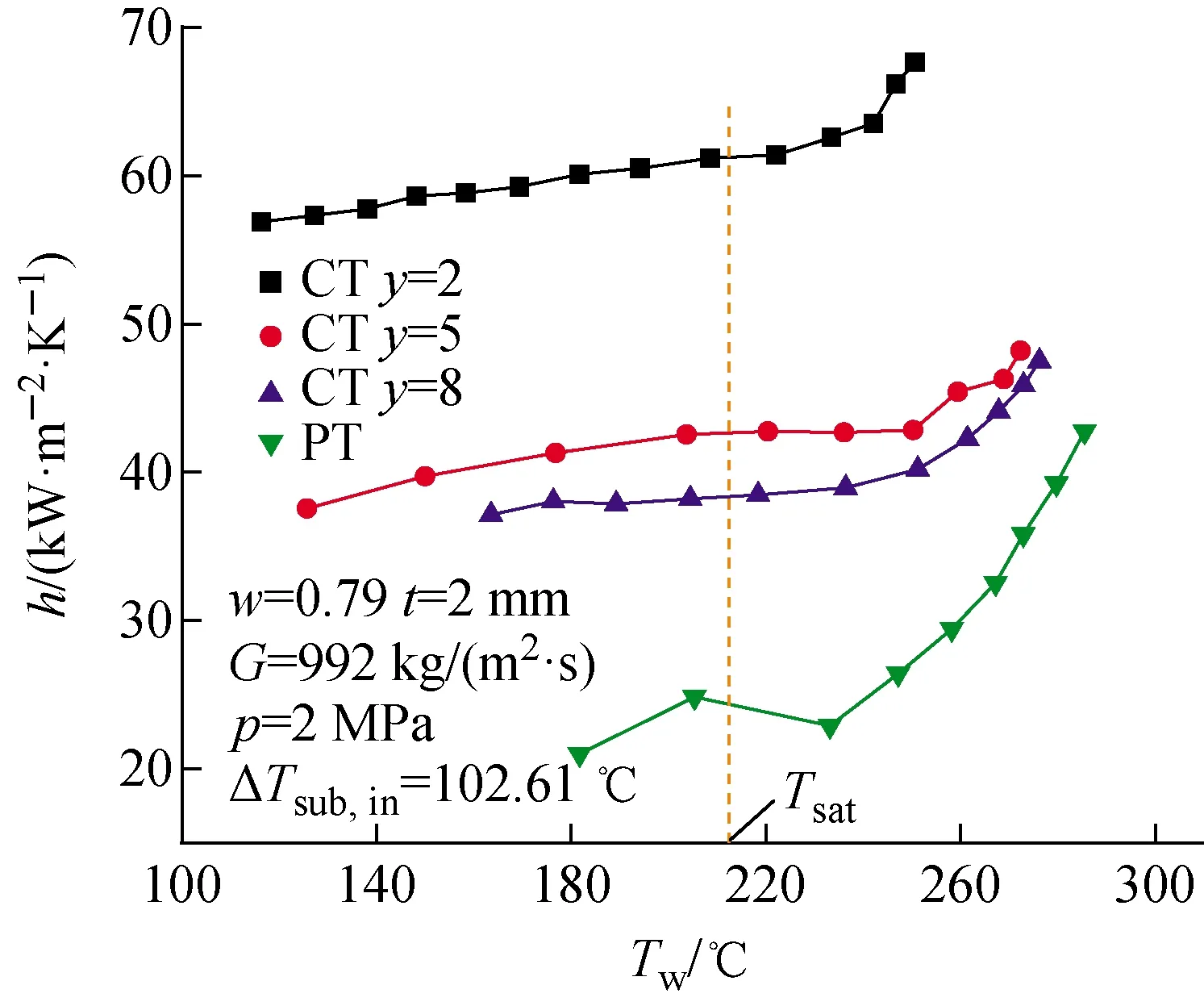
图10 不同扰动比y下复合换热管h随Tw的变化

3.3.2螺距 不同螺距下复合换热管的h随Tw的变化规律示于图11。从图11可看出，内螺纹的螺距越大，对流换热系数越高。在实验热流密度范围内，复合换热管在2 mm螺距时的对流换热系数较1.5 mm螺距时高约17%～39%。原因可解释如下，螺纹内肋可强化流体边界层处的湍流，增强流体在边界处的扰动，经过复合换热管内肋的强行切割，可破坏近壁面处汽膜的生成，有效减少受热表面附近的传热热阻，提升换热性能，故复合换热管螺距的增大可增大对流换热系数。

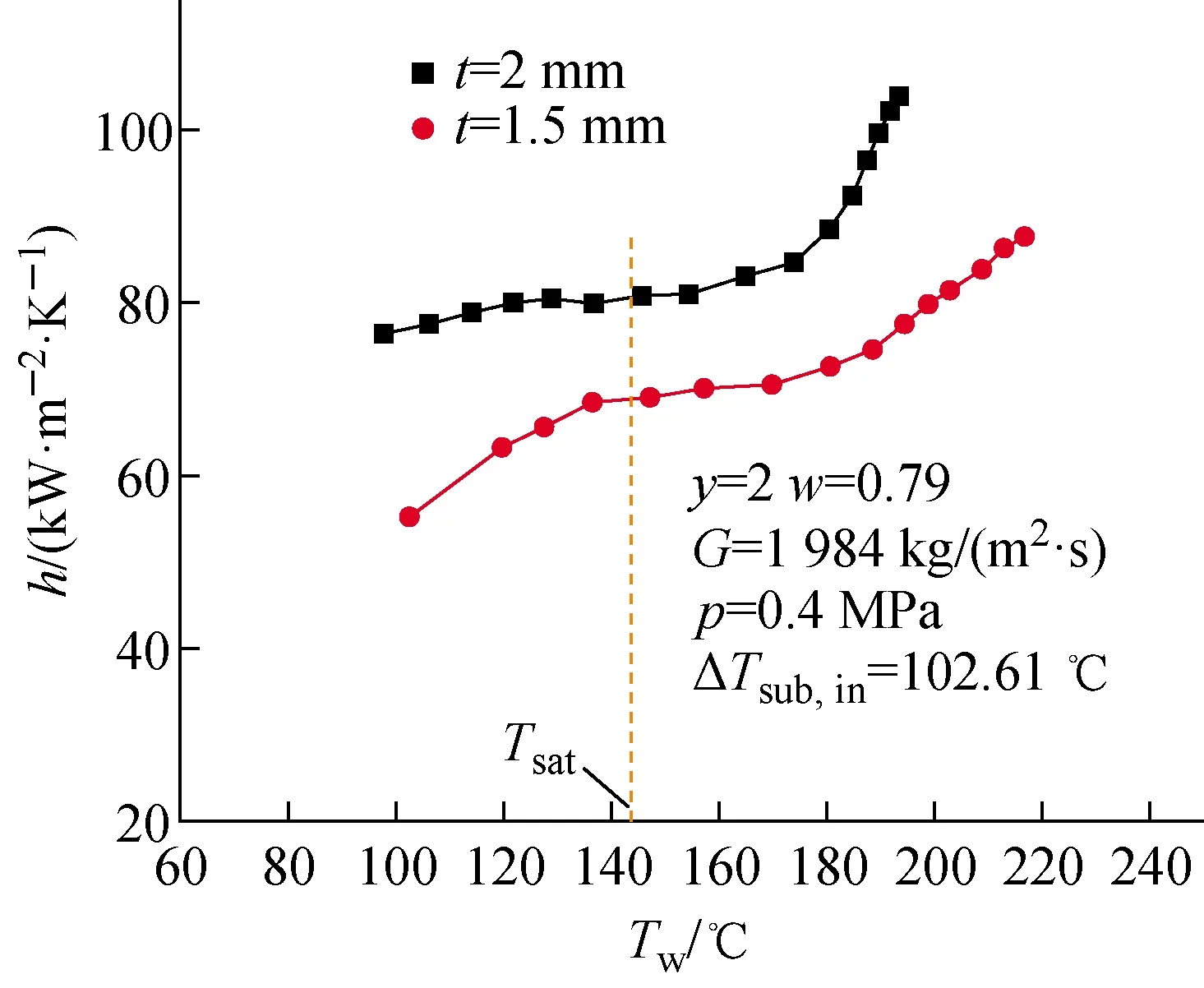
图11 不同螺距t下复合换热管的h随Tw的变化

3.3.3压力 复合换热管对流换热系数随压力变化的规律示于图12。从图12可看出，压力越小，对流换热系数越高。壁温较低时，不同压力对传热效果影响较小，此时管道壁温较低，流体处于单相流动区域。当热流密度逐渐增加时，复合换热管内壁温也逐渐升高，低压力条件(p=0.4、0.8、1.2 MPa)下，主流流体流动形式由单相流体传热逐渐过渡到过冷流动沸腾状态，压力减小，对流换热系数随壁温的增加有明显增大的趋势。可解释如下：随着压力的减小，过冷流体的饱和温度也减小，从而降低了流体进口过冷度，这更利于过冷流体产生核态沸腾，相同的变化趋势可参见文献[9]。高压力条件(p=1.6、2.0 MPa)下，流体对流换热系数随壁温的增大趋势越来越缓慢。压力较高时，流场的饱和温度较高，过冷流体难以发生过冷流动沸腾，流场主要为单相对流传热区域，对流换热系数随壁温的增加略有增加。

图12 不同压力p下复合换热管的h随Tw的变化

3.3.4质量流速 不同质量流速G下复合换热管的h-Tw和ΔTsat-q关系曲线示于图13。图13a显示，随着质量流速的增加，复合换热管的对流换热系数增加较明显。质量流速越大，复合换热管内主流流场的湍流强度、旋流强度和离心力越大，主流流场冷流体与近壁面热流体、气泡层之间的横向传质得到增强，加速近壁面处气泡从壁面脱离并在主流流场处凝结，强化了复合换热管道的传热传质特性。图13b显示，随着质量流速的增加，ΔTsat,ONB的发生略有延迟，同时，热流密度qONB均随质量流速的增大而逐渐增大。结合图13a，当壁温超过Tw,ONB时，质量流速对对流换热系数的影响逐渐减小。因为主流流体逐渐进入过冷流动沸腾区域，壁面处开始产生汽化核心。随壁温增加的同时，汽化核心增多，受热壁面和管内过冷流体之间，泡核沸腾传热形式所占比例逐渐高于单相流体对流传热，质量流速的影响开始减弱。

图13 不同质量流速G下复合换热管的h-Tw和ΔTsat-q关系

4 传热经验公式拟合

无论是内插扭带管还是内螺纹肋管，都有对应条件下的对流换热系数或努塞尔数公式，但对于本文所提出的内螺纹肋管，内插扭带这一新型复合换热管却没有过冷沸腾下的传热经验公式，因此本文主要对比4种现有不同传热经验公式，比较分析并寻求最符合复合换热管传热新公式的形式。

选取4种不同条件下的传热经验公式进行评价，其主要形式和适用条件列于表4。Yan等[25]和Liu等[26]的公式属于传热叠加模型，综合考虑了两相流沸腾传热中的强制对流换热以及核态沸腾换热的影响。叠加模型的基本形式一般可表示为：

表4 传热经验公式

htp=Fhsp+Shnb

(20)

其中：htp、hsp、hnb分别为两相流沸腾换热系数、单相对流换热系数和核态沸腾换热系数，kW/(m2·K)；F为强迫对流强化因子；S为核态沸腾抑制因子。

栾振博[27]和方贤德等[28]的公式属于无量纲预测公式，主要考虑对核态沸腾换热影响的修正。

4种不同传热经验公式计算值和实验值的对比示于图14，计算值和实验值的相对误差列于表5。其中Liu等[26]的公式相较于其他公式拥有最好的预测精度，平均绝对误差MAE为12.98%，均方根误差RMSE为15.81%，有80%的数据点误差在±20%之间。而Yan等[25]的预测结果与实验值间误差较大，其MAE和RMSE分别为33.36%和36.03%。栾振博[27]和方贤德等[28]的公式误差较小，两者的MAE分别为17.26%和22.52%，分别有45.3%和67.1%的数据预测误差在±20%之间。综合考虑两种预测模型，发现无量纲模型整体预测精度高于叠加模型，方贤德等[28]的公式在整体预测精度方面优于栾振博[27]的公式，更适合预测复合换热管的过冷流动沸腾传热系数，因此本文以方贤德等[28]的预测公式为基础，考虑螺径比t/Dh和扰动比y等的影响来预测本实验条件下复合换热管内的过冷沸腾传热特性公式。

表5 经验公式的预测精度

图14 不同公式的努塞尔数计算值和实验值的比较

方贤德等[28]将黏度比ln(bμl,sat/μl,w)纳入无量纲参数考虑中，作为提高流动沸腾传热关联式精度的重要参数，采用回归分析和最小二乘法得出水过冷流动沸腾传热新关联式，公式的相对误差在±20%之间，MAE为11.3%，预测精度较好。本文在该方法的基础上，结合其他无量纲预测公式中的相关参数可得出预测公式的形式，即Nu与Ja、Bo、Re、Pr、μl,sat/μl,w、y、t/Dh的关系：

Nu=aJabBocRePrd·

(21)

利用1stOpt软件的非线性拟合功能，将传热实验数据代入，提出了一个适用于复合换热管过冷流动沸腾传热准则关系式：

Nu=0.742Ja-0.27Bo0.825RePr-0.3·

(22)

为进一步确保新公式对实验数据预测的准确性，对比了新公式计算的Nucor随Nuexp的变化，结果如图15所示。可看出，实验值与预测值间的相对误差在±15%之间，MAE和RMSE分别为5.69%和7.55%，预测值和实验值一致性较好。这表明在该实验范围内，新传热公式可有效预测复合换热管过冷流动沸腾的努塞尔数。

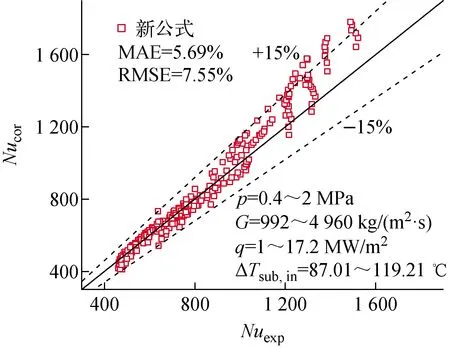
图15 新公式计算值与实验值的比较

5 结论

通过对复合换热管内过冷流动沸腾的实验研究，整理分析相关实验数据后得到如下结论。

1)4种不同管道中，复合换热管的对流换热系数最高。在实验条件范围内，复合换热管的对流换热系数分别较内插扭带管、内螺纹肋管和光管高约5%～98%、99%～102%和179%～184%。复合换热管的PEC为0.91～1.41，高于内插扭带管和内螺纹肋管。复合换热管可同时在流场近壁面区和湍流中心区起到协同复合强化换热的作用，达到一种协同效应，可获得更高效的换热性能。

2)扭带扰动比、螺距、压力和质量流速对复合换热管传热特性的影响结果表明，对流换热系数随扰动比的减小而增大；内螺纹的螺距越大，对流换热系数越高；壁温较低时，压力对传热效果影响较小。壁温较大时，压力对对流换热系数的影响明显增大；壁温较低时，随着质量流速的增加，复合换热管的对流换热系数增加较明显，较高质量流速可略推迟ΔTsat，ONB的发生。

3)对比分析了4个现有的传热经验公式，并分析了经验公式的误差精度。根据复合换热管的传热实验数据，以2个无量纲预测经验公式为基础，并用螺径比t/Dh和扰动比y进行修正，拟合出了本实验条件下复合换热管过冷流动沸腾的努塞尔数公式，实验值与预测值之间的相对误差在±15%之间，MAE和RMSE分别为5.69%和7.55%，表明实验数据与新公式预测值之间的一致性较好。