蒙特卡罗临界计算粒子并行动态负载均衡调权算法研究

付元光，刘 鹏，李 瑞，王 鑫，邓 力

(1.中国工程物理研究院 高性能数值模拟软件中心，北京 100088；2.北京应用物理与计算数学研究所，北京 100088)

蒙特卡罗临界计算是核临界安全分析的重要手段，由于蒙特卡罗方法具有几何描述精确、物理过程细致等特性，其临界计算结果常被视为参考解。使用蒙特卡罗方法模拟复杂问题时，需采用大规模并行计算和海量粒子样本确保问题收敛。研究发现，当并行规模较大时，裂变源分配方法和粒子权重调节策略将显著影响程序的负载平衡特征。本工作对比几种粒子分配与调权算法的性能，提出一种基于本地权重守恒的调权算法，通过实现动态负载平衡，以获得较高的加速比与并行效率。

1 蒙特卡罗临界计算流程

在蒙特卡罗临界计算中，通常采用裂变源迭代算法计算核系统的有效增殖因数。在该算法中，从某代初始裂变源分布抽样源粒子进行输运模拟，当粒子发生裂变时，记录当前位置作为下一代裂变源点用于下一代跟踪。系统的有效增殖因数keff可通过连续两代之间的裂变源总权重比值求得，通过多代迭代计算，keff均值和裂变源将逐渐收敛。然而在实际计算机程序的实现中，对于keff>1，会产生越来越多的裂变位置，直至占满内存；对于keff<1，会产生越来越少的裂变位置，直至为0。为保证每代模拟中子的总数和总权重守恒，防止无限增殖或消亡，需对粒子权重或裂变位置数进行纠偏[1-3]。

一般，串行临界计算的实现步骤[4-5]如下。在开始前需给定keff的初始猜测值k0、每代模拟粒子数N、循环代数It等参数以及一个初始裂变源分布，接着：

1)权重为1的N个中子逐个从初始裂变源发出并开始随机游动。单个中子每次发生碰撞时记录n个当前碰撞位置为新的裂变位置：

(1)

2)粒子发生碰撞或游动，会对keff的估计值产生贡献，一般有碰撞、吸收、径迹长度估计3种，以碰撞估计为例，单个中子每次碰撞对估计值的贡献为：

(2)

其中，fi为核素i的核子密度。

4)在新一代的模拟中，M个中子将从M个新的裂变位置发射，并重复1～3的步骤。需注意，新一代中子的出生权重问题，理论上M是N的无偏估计，但由于存在统计涨落，M会稍微偏离N，这时需调节粒子出生权重为N/M，以保证每代模拟粒子总权重守恒为N。

2 粒子并行算法研究

2.1 统一调节粒子权重的算法

实际发现这种算法存在严重的负载不均衡问题。使用了一个一维两区域单能量各向同性散射模型进行数值实验，模型参数如图2所示。将初始源设置在x=25 cm处，使用4个进程、不同样本数、循环200代展开模拟，随着模拟代数的增加，各进程上的裂变位置数变化情况如图3所示。可看出，裂变位置数在不同进程上的不均衡性随着每代模拟样本的减少而增加，在30 000粒子样本时，不同进程勉强能维持在同一水平；在3 000粒子样本时，不均衡性有所加剧；在300粒子样本时，0号进程不断减小直到为0，1号进程不断增大，3号进程即将变为0，不均衡已非常显著。可推断，当每代模拟样本量越少时，计算不均衡问题越严重。

图2 数值实验模型

a——每代模拟30 000；b——每代模拟3 000；c——每代模拟300

2.2 Master-Slave算法

如上所述，在初始虽然给每个进程均匀分配了裂变位置数，但随着模拟进行，本地裂变位置数出现涨落，使得负载不均衡出现。Master-Slave算法通过在每个循环代结束、下一代开始前进行裂变位置的收集和再分配，以达到平衡各进程间权重的效果，代表程序是MCNP。若使用m+1个进程并行模拟，则会产生1个Master进程和m个Slave进程，Master进程负责数据收集与分发，Slave进程进行粒子并行模拟任务。每代模拟完毕后，各Slave进程将本地裂变位置发送给Master，Master搜集所有信息后平均分配成m份，再发送到各Slave进程上，保证每代各Slave进程的模拟权重相等。图4给出一个N=3 000、m=5的示例。Master-Slave算法由于每代循环都需进行全局收集和分发通信操作，通信耗时会随着裂变位置数、循环代数的增大而显著增长。

图4 Master-Slave算法示例

2.3 Nearest Neighbor算法

为减少每代循环间的通信数据量，以OpenMC为代表的程序提出Nearest Neighbor算法[6]。该算法抛弃了Master进程，而在各Slave进程上点对点通信必要的数据。若使用m个进程并行模拟N个粒子，则每个进程初始分配到N/m个粒子，1代结束后，每个进程上产生的粒子不等于N/m，将新的粒子排序编号，对j号进程而言，设其本地所有的粒子中第1个和最后1个编号分别是aj、bj，若ajjN/m则从j-1号进程接收aj-jN/m个粒子；类似地，若bjj(N+1)/m，则将bj-j(N+1)/m个粒子发送给j+1号进程。图5给出一个N=3 000、m=4的示例。Nearest Neighbor算法能保留一部分本地的裂变位置，避免了所有位置的收集分发操作，使用点对点通信，有效减少了通信数据量。

图5 Nearest Neighbor算法示例

2.4 调节本地出生粒子权重的算法

图6 改进的粒子并行的源迭代算法

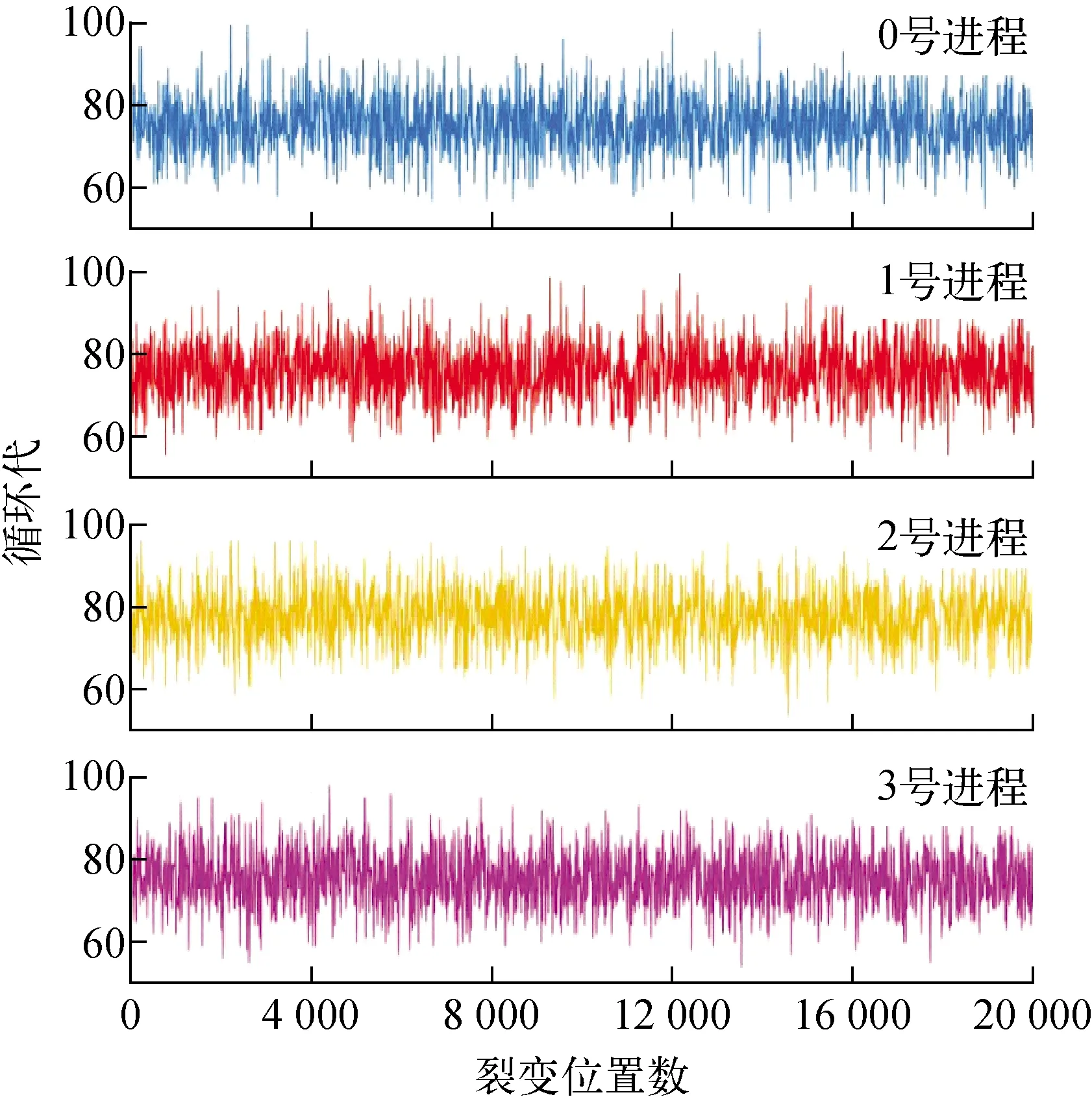
图7 不同进程上裂变位置数随循环代的变化

本算法的优点在于通信量为上述诸算法中最小，由式(2)可知，每代的keff仍需全局规约求和，除此之外本算法没有其他需要通信的数据，而keff数据量较粒子的裂变位置信息数据量基本可忽略不计。本算法的不足之处在于，无法保证串并行一致，对比之前的几种算法，可发现它们均能保证每个进程上的粒子出生权重完全相同，这样只要保证每个粒子分配到的随机数序列与串行完全相同，那么无论不同进程间如何分配粒子，都会得到与串行相同的结果，而这对于常用的乘加同余随机数发生器是易实现的；对于本算法，每个进程在每次循环代的出生权重各不相同，结合keff估计的累加式(2)，可发现权重的差异影响keff的计算结果，即使每个粒子使用与串行完全相同的随机数序列，也无法还原串行下每个粒子累加时的权重，进而造成串并行的不一致。尽管如此，对蒙特卡罗随机模拟而言，只要计算结果可收敛，即使串并行不一致也可接受。

3 数值结果

3.1 压水堆单栅元测试

用1个带有全反射边界条件的压水堆棒栅算例[8]，模拟3×106个粒子，采用3 000粒子×1 000代、30 000粒子×100代、300 000粒子×10代 3种模式测试上述算法的加速比，结果列于表1～4，其中计算耗时主要包括粒子的跟踪与通信时间，去除了初始化、截面读取等其他耗时。

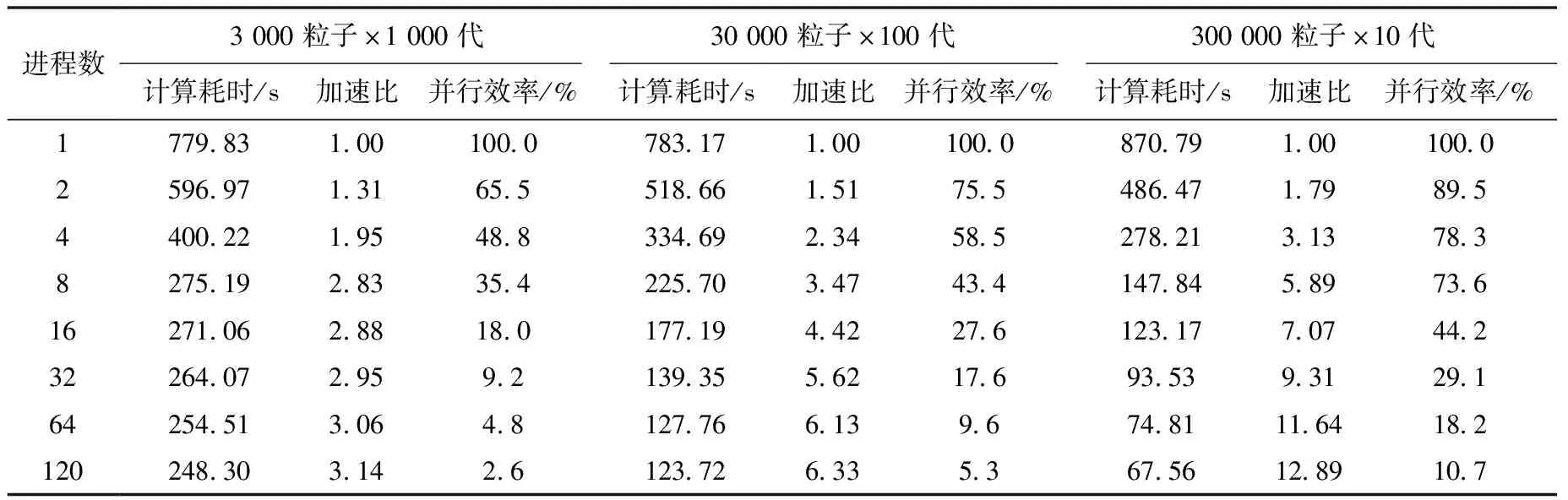
表1 统一调节粒子权重算法并行测试结果

由表1可看出，对于统一调节粒子权重算法，加速比很差，可推测由于负载不均的存在，进程存在大量等待现象。由表2可看出，Master-Slave算法加速比整体有一定程度提升，每代粒子数越少、代数越多，加速比越差，对于3 000粒子×1 000代的情况，在120核时加速比甚至出现了下降，这主要因为代数越多，通信的次数越多，通信的调用越频繁，额外开销越大，加速效果下降越明显。由表3可看出，Nearest Neighbor算法加速比又有进一步提升，对于少样本、多代数仍存在加速比较低的现象，但较Master-Slave算法已改善很多。从表4可看出，本工作提出的新算法加速性能整体优于Nearest Neighbor和Master-Slave。各算法的共同现象是少样本、多代数设置下加速比最低，这是由于源迭代算法总是在每代之间进行通信，越多的代数意味着越多的通信操作，因此在蒙特卡罗临界计算粒子并行模拟时，最好使用多样本、少代数的设置。

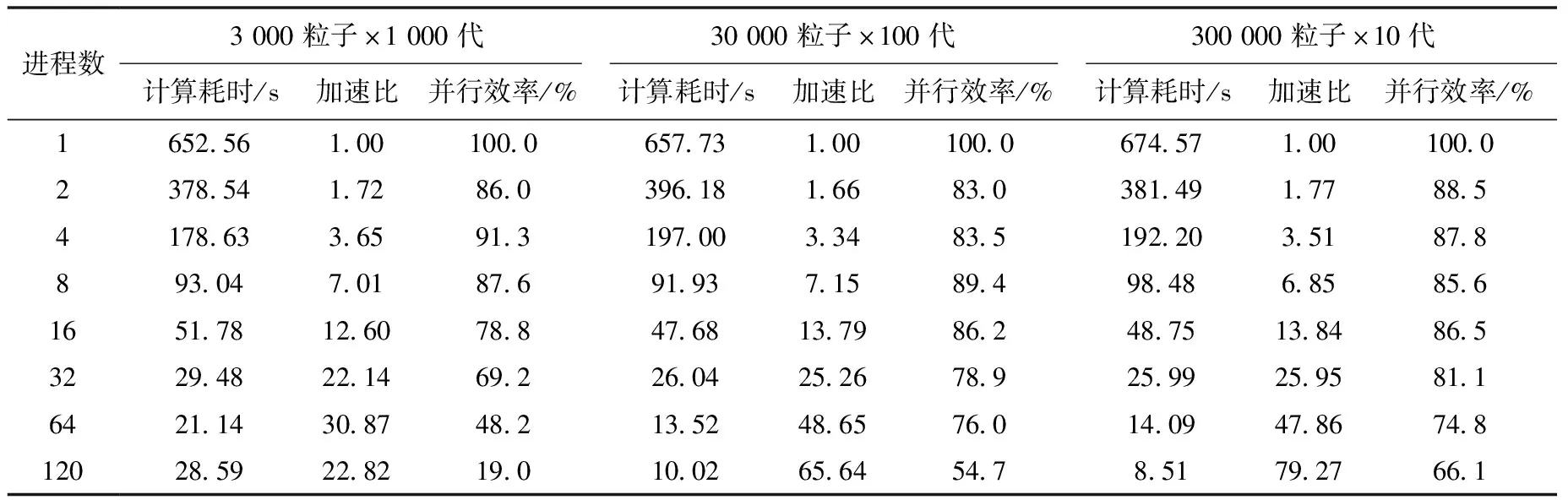
表2 Master-Slave算法并行测试结果(单栅元)

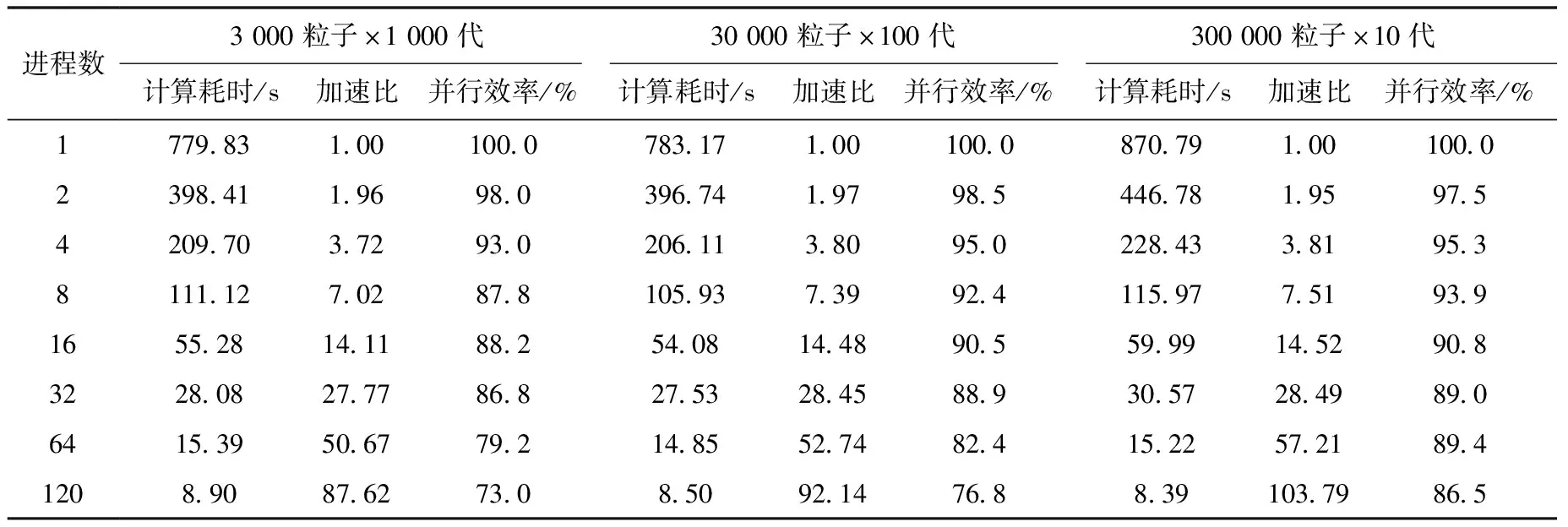
表4 本地权重调节算法并行测试结果(单栅元)

为说明本工作算法在串并行不一致方面的影响，统计了3 000粒子×1 000代情况下使用不同进程数计算keff的结果，列于表5。可看出，最大值与最小值的差距为62 pcm，说明算法虽无法保证串并行一致，但不影响收敛性。

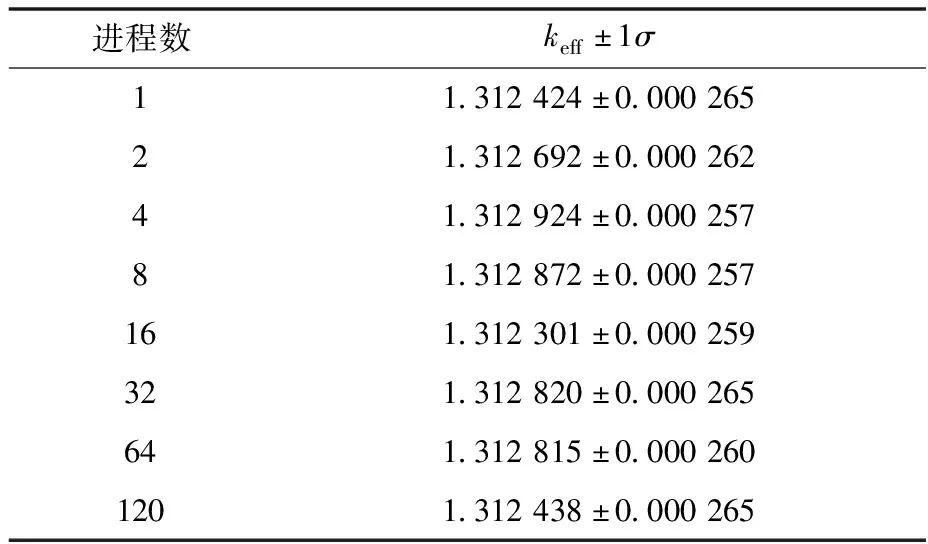
表5 使用不同进程数计算keff结果对比

3.2 压水堆2×2组件测试

参考C5G7-2D基准题[9]构造了一个2×2组件排列的模型，其中燃料棒尺寸、栅距、反射层等几何参数以及边界条件设计和C5G7-2D完全相同，略有差别的是所有棒束(包括导向管位置)均使用二氧化铀。采用每代10 000粒子×1 000代、100 000粒子×100代、1 000 000粒子×10代 3种模式测试加速比，对于统一调节权重算法，由上节可看出其效率过差，因此没有再进行测试，仅就Master-Slave、Nearest Neighbor和新算法进行测试，结果列于表6～8。

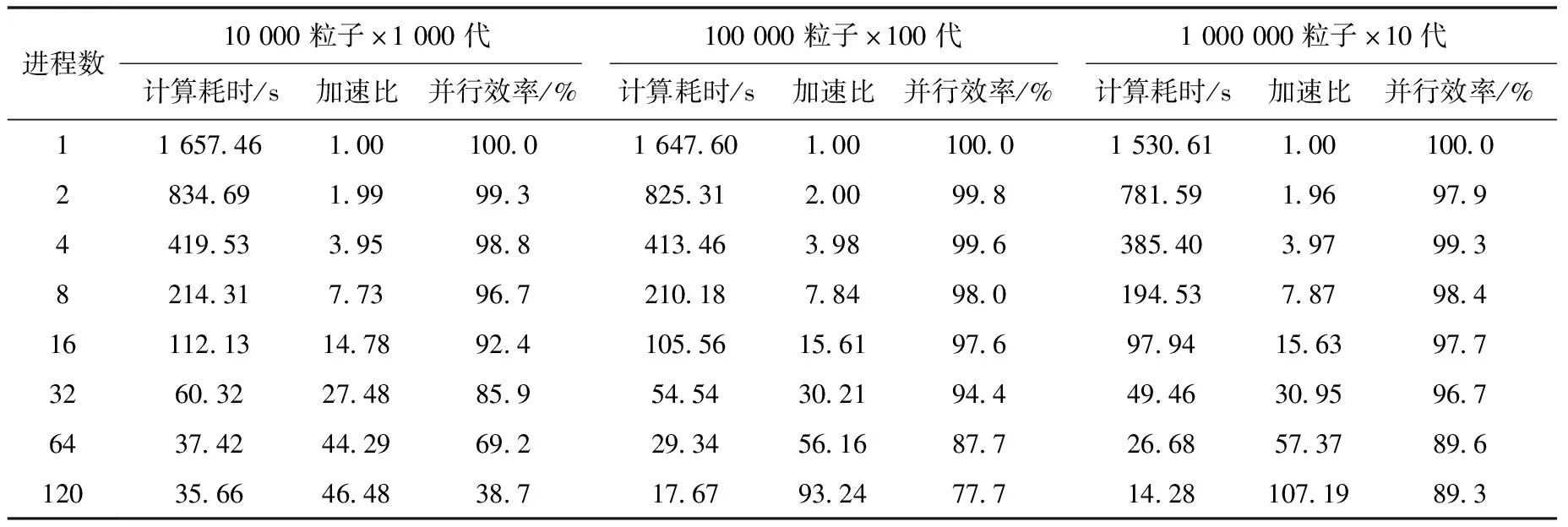
表6 Master-Slave算法并行测试结果(2×2组件)

表7 Nearest Neighbor算法并行测试结果(2×2组件)

表8 本地权重调节算法并行测试结果(2×2组件)

可看出，类似上节的测试，新算法整体上加速效果优于前两者；Master-Slave算法在少粒子、多代数设置下仍会出现加速比快速下降的现象；值得注意的是，Nearest Neighbor算法在多粒子、少代数设置下性能较Master-Slave差，原因分析如下：当进程数增大时，每个核分配的计算任务变少，计算时间缩短，通信时间所占比重增大，由于OpenMC的串行速度最快，随着进程变多，其通信占比提升更明显，上述测试的样本量对于OpenMC略显不足，增大样本量可提升OpenMC性能。

3.3 全堆大规模测试

在天河2超算上使用BEAVRS模型[10]测试本工作算法的并行效率，BEAVRS是由MIT提出的压水堆堆芯模拟验证基准题，具有193个燃料组件和17×17棒束结构，对BEAVRS进行精细描述需百万量级栅元，适用于较大规模的并行测试。BEAVRS具有两个循环周期的实测数据，尽管计算这些内容需多物理耦合，但出于并行效率测试的目的，本工作仅对其初始冷态零功率工况进行蒙特卡罗输运模拟。所有涉及到的测试时间均为去除数据初始化步骤(输入解析，截面读取、广播，内存分配等)后余下的源迭代流程的执行时间。

对BEAVRS进行了pin-by-pin精细建模，燃料棒轴向划分16层，模型总栅元数达到540余万。首先测试了弱可扩展并行效率，通过调节粒子样本数以控制程序计算量，样本数的设置、计算结果、并行效率等列于表9。然后测试了强可扩展并行效率，固定每代使用107粒子、循环500代，计算结果列于表10。可以看出，相对于128进程，4 800进程的弱可扩效率达到92.54%，强可扩效率达到81.47%，说明算法具有较好的并行性能。keff最大值与最小值差距为35 pcm，说明算法不会影响计算的收敛。

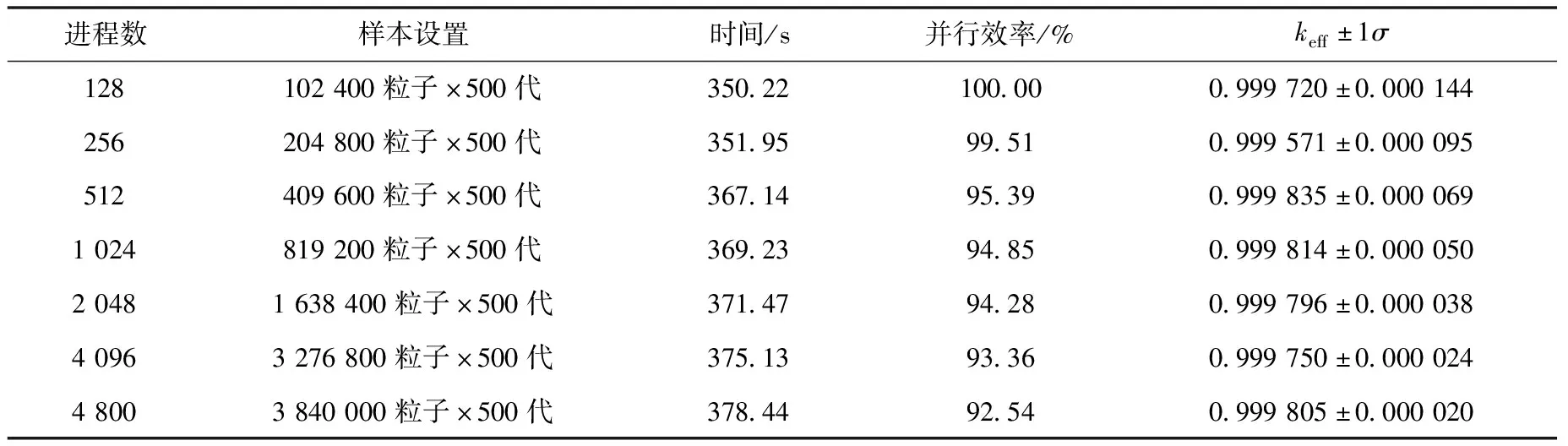
表9 弱可扩展并行效率测试结果

表10 强可扩展并行效率测试结果

4 结论

在蒙特卡罗临界计算粒子并行模拟中，随机涨落的存在会显著影响并行的负载均衡特性，如果不平衡每个进程上的粒子数，将会发生严重的负载不均衡现象，特别当每代模拟数目较小、代数较多时，负载均衡更差。Master-Slave算法通过粒子的全局收集与再分配，实现各进程上模拟权重的平衡，但会引入较多通信操作。Nearest Neighbor算法通过保留部分本地粒子、在相邻结点间点对点通信部分粒子，有效降低了通信数据量。本工作提出一种基于本地权重期望值守恒调节出生粒子权重的方法，可以保证随着循环代数增加，各进程上的裂变位置数和本地权重不出现显著偏离，负载均衡较好，且数据通信操作更少。基于压水堆棒栅、组件问题，通过不同粒子数和循环代数设置，测试了各算法的加速性能，本工作提出的算法较Master-Slave和Nearest Neighbor算法获得进一步提升，特别对于少粒子、多循环的参数设置，算法提升最为明显。在天河2超算上测试了算法的并行效率，BEAVRS冷态零功率计算4 800进程相对128进程的弱可扩和强可扩效率可以达到92.54%和81.47%以上。